Review Article
Austin J Anat. 2014;1(3): 1012.
Using Artificial Neural Networks for the Forecasting of the Correct Skeletal System Development in Children
Gworys B1*, Kordecki H1,3 and Brukiewa R2
1Department of Anatomy, Wroclaw Medical University, Poland
2NZOZ „Nasz Lekarz” in Torun, Poland
3Institute of Computer Technology, Automatics and Robotics, Wroclaw University of Technology, Poland
*Corresponding author: Gworys B, Department of Anatomy, Wroclaw Medical University, 6a Chalubinskiego St, 50-368 Wroclaw, Poland.
Received:May 20, 2014; Accepted: July 09, 2014; Published: July 14, 2014
Abstract
Background: The aim of the work was to evaluate changes in bone density taking place in the femoral bone of healthy children depending on the amount of fat tissue and advancement in puberty.
Methods: A sample of 370 children chosen at random from the public school, of both sexes’ (190 boys aged from 7.2 to 156 years and 180 girls aged from 5.6 to 14 years) was examined in Torun, at the “Nasz Lekarz” outpatient clinic. Using DXA method an individual evaluation of femoral bone density in particular measurement fields was performed. Taking BMI parameter into account children were divided (separately boys and girls) into groups in pre-pubertal phase, pubertal phase and post-pubertal phase. The evaluation of statistic differences between groups was performed using variance analysis. To estimate the variability of femoral bone density artificial neural networks (RBF) were chosen. The use of this method allowed individual prediction of bone density based on current age and BMI value.
Results: Girls have 0.1 g/cm2 less dense femoral bone than boys. Femoral bone density rises with the pubertal spurt with girls by 0.22 g/cm2, with boys by 0.16 g/cm2.
Conclusion: It was ascertained that there is a statistically significant increase in femoral bone density dependent on the age of the child. For boys it is larger in the later phase of puberty. Differences of bone density changes depending on sex were confirmed. The bone density prediction based on current age and BMI for small group of children was performed and its results appeared to be very promising.
Keywords: Bone density; Puberty; Artificial neural networks
Introduction
Osteoporosis and osteopenia are medical conditions that cause ill-health for patients and costs for society in terms of treatment. A prophylactic intervention that would prevent osteoporosis by providing a peak bone mineralization could result in a considerable decrease in the number of osteoporotic fractures in later life. Therefore a definition of the onset of pathological change and an ability to predict these changes would be of benefit to administrative and health care authorities and, not least to potential future sufferers. The aim of the work is the evaluation of changes in bone density taking place in femoral bone in healthy children depending on the amount of fat tissue and advancement in puberty. At the same time methods of individual prediction of bone density basing on age and BMI value was described.
Seeman [1] noticed that research on twins and families proves that the peak bone mass is determined by predominantly genetic factors and is to a high degree hereditary. Gilsanz et al. [2] Shoved that puberty has an essential effect on the final bone mass formation and bone density. Results of analysis performed by team Clark [3] suggests that there is a connection between low bone density and fractures in children but he also mentioned that well conducted and extensive research is needed to confirm this fact.
Methods
Material for the work contains examination results of 370 children, of both sexes’ (190 boys aged from 7.2 up to 16 years and 180 girls aged from 5.6 to 14 years) examined in Torun, at the “Nasz Lekarz” outpatient clinic chosen at random from public school No 24. The individual evaluation of morphological age based on anamnesis and the estimation of secondary sex characteristics age was performed before the examination of every child. Basing on this criterion, children were divided into 6 groups: boys in pre-pubertal phase – 63 individuals; pubertal phase – 64 individuals; in late pubertal phase – 63 individuals; girls in pre-pubertal phase – 60 individuals; in pubertal phase – 60 individuals in late pubertal phase – 60 individuals.
Using DXA method the evaluation of femoral bone density in particular measurement fields was performed. The BMD-FQ (femoral neck), BMD-FT (greater trochanter), BMD-FU (femoral shaft), CMD-FV (total femoral bone density) were taken into account. For both sexes and every measured parameter, statistically significant differences between mean values in separate age categories were examined using variance analysis (ANOVA).
To estimate the bone density in particular regions of femur depending on simultaneously age and BMI value artificial neural networks were used. Expecting non-linear dependences two layers networks type RBF (Radial Based Function) were chosen. The usefulness of RBF networks in case of nonlinearity, among the others, was tested with positive results by Blake [4].
Results
In tables 1 and 2 the basic statistical parameters of the investigated material are shown.
N
M
S
Min-max
Neck of femur
190
0,86
0,13
0,42-1,34
Greater trochanter
190
0,73
0,13
0,49-1,24
Body of femur
190
0,98
0,17
0,58-1,58
Total femur
190
0,89
0,14
0,55-1,37
Table 1: Femur bone density of boys (N – number of patients, M - average, S - standard deviation).
N
M
S
Min-max
Neck of femur
180
0,77
0,12
0,48-1,11
Greater trochanter
180
0,63
0,12
0,32-0,93
Body of femur
180
0,87
0,15
0,58-1,38
Total femur
180
0,78
0,13
0,51-1,13
Table 2: Femur bone density of girls (N – number of patients, M - average, S - standard deviation).
Results of variance analysis are shown in Table 3. It was ascertained in the case of boys that femoral bone densities increases during the pubertal spurt by 0; 16 g/cm2, and during the transition from pre-pubertal to pubertal phase is lower than during transition to post-pubertal phase. In case of girls increasing of femoral bone density in this period is almost linear and equals 0.22 g/cm2. In the case of girls the increasing of bone density is near 0.1 g/cm2 then for with boys. Within one sex changes of bone density in every examined segments of femur are similar.
Boys
Girls
Neck of femur
I
II
I
II
II
+
II
+
III
+
+
III
+
+
Greater trochanter
I
II
I
II
II
II
+
III
+
+
III
+
Body of femur
I
II
I
II
II
II
+
III
+
+
III
+
+
Total femur
I
II
I
II
II
II
+
III
+
+
III
+
+
Table 3: Results of variance analysis (I – pre-pubertal phase, II - pubertal phase, III - post-pubertal phase) (+) – statistical significance.
The aim of the second part of research was to explore the bone density dependency simultaneously on the age and BMI, separately for boys and girls. So, the following relationship was considered:
Where: BMD – bone density in one of four femur regions, A: age in months, BMI – body mass index.
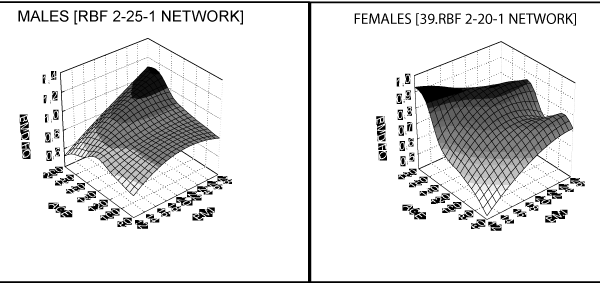
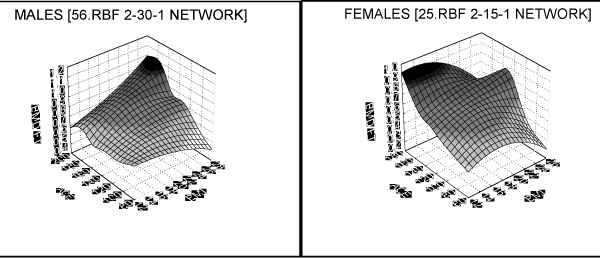
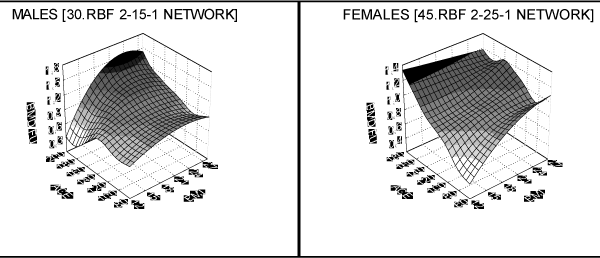
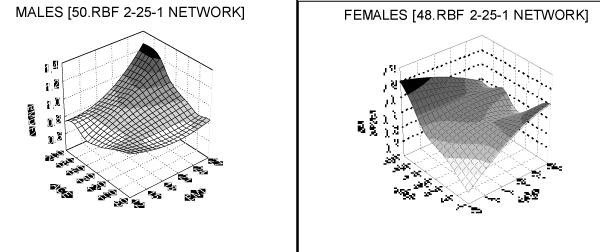
The dependency (nonlinear function F) was estimated using two layer RBF networks. One of the examples of using RBF networks for the nonlinear dependencies estimation can be found in the paper of Bahar and co. In effect 8 network structures were received. Each network gave the best approximation of function F and was chosen from variety of networks with different number of neurons in hidden layer. The choice was made for four femoral regions, separately for both sexes. It was assumed that the best network was the one with most accurate results of testing. Testing quality was evaluated using mean squared error between network output and real output. Graphically results are shown in Figures: 1-4.
Figure 1: Neck of femur as a function of age and BMI.
Figure 2: Greater trochanter as a function of age and BMI.
Figure 3: Body of femur as a function of age and BMI.
Figure 4: Total femur as a function of age and BMI.
Last phase of research was to check the usefulness of method by the application of received networks in practice. Groups of 7 boys and 10 girls, selected outside of learning network sequences were considered. For each individual the bone density in four femoral regions was calculated using the appropriate network. To evaluate quality of prediction process two parameters were chosen: the correlation coefficient between real density value and the value obtained in prediction process and the average relative prediction error. That kind of RBF network application can be found for example in the paper of Awad et al. The average relative prediction error was calculated as the average of absolute values of differences between predicted and real densities divided by real density value, expressed in percents. The exact formula is given below.
Where: RE – average relative error, RV – real value, PV – prediction value.
Correlation coefficients for boys between real and predicted bone density are very high and are in the range between 0.53 for BMD_ FV (total femoral density) to 0.91 for BMD_FU (femoral shaft). High coefficient values obtained show good prediction quality. The average relative prediction error is low and is changing from 6% for BMD_FQ (femoral neck), to 7.4% for BMD_FT (greater trochanter), which confirms good predictive value thesis much more. Correlation coefficient for girls is in the same value ranges as for boys. Average, relative prediction error for girls is slightly higher and its minimal value is 7.2% for BMD_FT (greater trochanter) and maximal 8.6% for BMD_FV (total femoral bone density).
Discussion
The social consequences of osteoporosis and osteopenia result in high costs of treatment and rehabilitation and because of that cause interest of many specialists in the regular development of the osteoskel et al system in childhood. Body composition during puberty is an indicator of changes that happen in maturing organisms and contains key information concerning present and future state of health [5, 6]. It is simultaneously, as described in the paper of Siervogel et al. [7], indicator of the chronic diseases beginning and allows estimating risk of those diseases and possibly early intervention. The estimation of bone density changes during puberty should be the basis of child’s physical examination and the possible deviation from normal, and should lead to possible detailed densitometric examination and to give prophylactic recommendations. Densitometric examinations are still too expensive to use them as routines to evaluate the mineral density of children bones. Substitute, cheaper ways to estimate bone density are investigated, to allow selection of risk groups for detailed densitometry examinations described for example by Siervogel et al. [7] and Lorenc et al. [8]. In the first stage of research the evaluation of bone density changes during puberty is performed. Obtained results indicate that mean bone tissue density in every femur region is higher in boys than in girls. There is observed statistically significant bone density increase together with age within the same sex. Peak bone mass increase in both sexes is observed one year after puberty [9]. Authors emphasize the influence of sex and bones size on densitometric results, see papers written by Baxter-Jones et al. [10] and Weaver et al. [11]. It was also stated that bone density in both sexes’ statistically significant increases together with BMI values, up to gained peak bone mass. In girls slight decrease of density during pre-puberty phase is exposed. This was not observed in examined boys. Appreciable, statistically significant influence of BMI on the examined bone density authorized us to take it into consideration. Using artificial neural networks to estimate bone density and then to apply them to the bone density prediction allow avoidance of expensive densitometry examinations and perform the examinations only for those children, for which predicted bone densities are abnormal. It was demonstrated that applying artificial neural network to children skeletal system diagnostics and its regular development, growing and mineralization prediction gives very promising results. Evidence is the third stage of research, where the quality of prediction was tested. Correlation coefficients between the real bone density value and predicted value are very high and reach 0.91, with simultaneously low, not exceeding 8.6%, relative prediction error.
Conclusion
The average bone tissue density in every femoral bone region is higher in boys than in girls. There is observed a statistically significant bone density increase together with age within the same sex. Peak bone mass increase in both sexes is observed one year after puberty period. Using artificial neural networks to evaluate bone density enables a simple and inexpensive routine of examination and screening and permits selection to densitometry examinations only those cases with bone mineralization disorder. Applying artificial neural networks to the children skeletal system diagnostics and its regular development prediction allows estimation with a large probability and low prediction error.
References
- Seeman E. Clinical review 137: Sexual dimorphism in skeletal size, density, and strength. J Clin Endocrinol Metab. 2001; 86: 4576-4584.
- Gilsanz V, Gibbens DT, Roe TF, Carlson M, Senac MO, Boechat MI, et al. Vertebral bone density in children: effect of puberty. Radiology. 1988; 166: 847-850.
- Clark EM, Ness AR, Bishop NJ, Tobias JH. Association between bone mass and fractures in children: a prospective cohort study. J Bone Miner Res. 2006; 21: 1489-1495.
- Blake AP, Kapetanios G. A radial basis function artificial neural network test for neglected nonlinearity. Econometrics Journal. 2003; 6: 356–372.
- Bahar HB, Sokouti B. Estimating K, C variable parameters of a weighting system using RBF neural networks. ARPN Journal of Engineering and Applied Sciences. 2009; 4: No. 4.
- Awad M, Pomares H, Rojas I, Salameh O, Hamdon M. Prediction of time series using RBF neural networks: a new approach of clustering, The International Arab Journal of Information Technology. 2009; 6: No. 2.
- Siervogel RM, Demerath EW, Schubert C, Remsberg KE, Chumlea WC, Sun S, et al. Puberty and body composition. Horm Res. 2003; 60: 36-45.
- Lorenc RS, Kryskiewicz E. Diagnostics of osteoporosis at children. Terapia. 2005; 13: 9-11.
- Ring EFJ. Recent developments in bone densitometry of children. Pediatr Med Rodz. 2005; 1: 157-164.
- Baxter-Jones AD, Mirwald RL, McKay HA, Bailey DA. A longitudinal analysis of sex differences in bone mineral accrual in healthy 8-19-year-old boys and girls. Ann Hum Biol. 2003; 30: 160-175.
- Weaver CM, McCabe LD, McCabe GP, Novotny R, Van Loan M, Going S, et al. Bone mineral and predictors of bone mass in white, Hispanic, and Asian early pubertal girls. Calcif Tissue Int. 2007; 81: 352-363.