Comparison of Kinetic Models for Dual-Tracer Receptor Concentration Imaging in Tumors

Research Article

Austin J Biomed Eng. 2014;1(1): 1002.

Comparison of Kinetic Models for Dual–Tracer Receptor Concentration Imaging in Tumors

Nazanin Hamzei1, Kimberley S Samkoe2,3, Jonathan T Elliott2, Robert W Holt2, Jason R Gunn2, Ting-Yim Lee4 Tayyaba Hasan5, Brian W Pogue 2,3,4 and Kenneth M Tichauer1*

1Department of Biomedical Engineering, Illinois Institute of Technology, USA

2Department of Medical Biophysics, Dartmouth College, USA

3Department of Surgery, Dartmouth Medical School, USA

4Department of Medical Biophysics, Western University, Canada

5Department of Dermatology, Massachusetts General Hospital, USA

*Corresponding author: :Kenneth M Tichauer, Biomedical Engineering, Illinois Institute of Technology, 3255 S Dearborn St, Chicago, IL, 60616, USA.

Received: January 20, 2014; Accepted: February 24, 2014; Published: March 05, 2014

Abstract

Molecular differences between cancerous and healthy tissue have become key targets for novel therapeutics specific to tumor receptors. However, cancer cell receptor expression can vary within and amongst different tumors, making strategies that can quantify receptor concentration in vivo critical for the progression of targeted therapies. Recently a dual–tracer imaging approach capable of providing quantitative measures of receptor concentration in vivo was developed. It relies on the simultaneous injection and imaging of receptortargeted tracer and an untargeted tracer (to account for non–specific uptake of the targeted tracer). Early implementations of this approach have been structured on existing “reference tissue” imaging methods that have not been optimized for or validated in dual–tracer imaging. Using simulations and mouse tumor model experimental data, the salient findings in this study were that all widely used reference tissue kinetic models can be used for dual–tracer imaging, with the linearized simplified reference tissue model offering a good balance of accuracy and computational efficiency. Moreover, an alternate version of the full two–compartment reference tissue model can be employed accurately by assuming that the K1s of the targeted and untargeted tracers are similar to avoid assuming an instantaneous equilibrium between bound and free states (made by all other models).

Keywords: Dual–Tracer; Tumors; GARTM; BFM

Introduction

In cancer research, 95% of new therapeutics fail to demonstrate significant outcomes in clinical trials and are therefore abandoned after substantial investment [1,2], even though many of these therapeutics are designed to target cancer–specific receptors, being the products of highly sophisticated studies in cancer molecular expression [3]. While there is no consensus as to why so many drugs are failing clinical trials, it is clear that drug developers require new non–invasive methods to quantify cancer receptor concentrations in vivo in order to better understand the relationship between receptor availability, and drug targeting and binding [4]. Unfortunately, it has been difficult to extract quantitative information about tumor receptor concentrations with conventional molecular imaging strategies. They typically involve injecting a subject with an imaging tracer targeted to a receptor of interest, waiting some duration of time for any unbound tracer to exit the tissues, and assuming the remaining measured signal arises from tracer that is bound to its specific receptor. The problem is that drug delivery research in oncology has demonstrated that many physiological and pathophysiological factors (e.g., blood flow, vascular permeability, interstitial pressure, and lymphatic drainage) can significantly influence the uptake of a targeted tracer in a tumor [5–8].

In response, “dual–tracer” imaging utilizes the uptake of a second tracer, similar to the targeted tracer but designed to be untargeted, to account for any non–receptor mediated uptake of the targeted tracer [9–11]. This approach was recently advanced by the development and validation of the first imaging methodology capable of quantifying receptor concentrations tumors [12]. The importance of using this “dual–tracer” approach over “reference tissue” approaches which have been used for over a decade in brain studies to quantify neurotransmitter receptor concentrations [13] was also demonstrated to be critical when attempting to quantify receptor concentration in tumors [14].

To date, the dual–tracer Receptor Concentration Imaging (RCI) approaches have rather indiscriminately employed one of the two early reference tissue models, Lammertsma and Hume’s “simplified reference tissue model” [15] and Logan et al.’s “graphical analysis” approach [16], for no other reason than that they were easily adaptable to the dual–tracer framework. Even though many of the assumptions made in reference tissue models hold for dual–tracer RCI, it is not necessary that these models are optimal since additional assumptions can be made with dual–tracer RCI: e.g., that the delivery rates (K1) of both tracers are the same if the chemical properties of the tracers are similar. Using both simulated and experimental data, the current study was carried out to identify the optimal data analysis workflow for translating targeted and untargeted tracer uptake curves in tumors to receptor concentration images, with particular emphasis on noise characteristics and computational cost of kinetic model data fitting.

Theory

Compartment models for dual–tracer kinetic analyses.

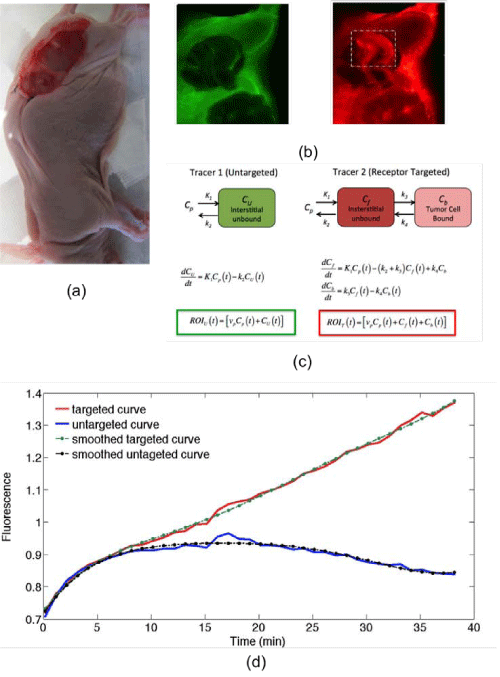
Reference tissue compartment models are ideally suited for dualtracer RCI since the setup of the dual–tracer compartment model (Figure 1) is nearly identical to that of the reference tissue model [15]. Both models recognize that non–specific uptake of a targeted tracer can significantly affect the relationship between tracer uptake and tracer binding or receptor concentration. The reference tissue model accounts for binding by employing the temporal uptake of the targeted tracer in a region devoid of targeted receptor (reference tissue) to account for non–specific uptake; while the dual–tracer approach employs the uptake of a second tracer, similar in structure to the targeted tracer but untargeted, in the same tissue as the targeted tracer to account for non–specific uptake. On the surface it would seem that whatever kinetic model was best for one approach would also be best for the other, but there are subtle differences between the approaches that can impact the choice of the optimal kinetic model:

  1. The plasma input function, Cp: in the reference tissue model, the reference input and the region–of–interest input intrinsically have the same plasma input function, so this is not a concern; however, in the dual–tracer model, both tracers used must have the same plasma kinetics of the course of imaging.
  2. K1⁄k2 equivalency: in reference tissue models, it is assumed that the ratio of the tracer’s extravasation and tissue–efflux rates, K1 and k2, are equivalent in the reference tissue and the region of interest; whereas, dual–tracer models assumes that these leakage kinetics are the same between tracers in all tissues.

In this study, six different reference tissue models are evaluated in terms of their ability to accurately and efficiently estimate tumor cellsurface receptor concentration from dual–tracer data. The models included 1) the “Full Reference Tissue Model” [FRTM] [17,18], later modified to a “reduced Full reference Tissue model” [Reduced FRTM] 2) the “Simplified Reference Tissue Model” [SRTM] [15], 3) the original Graphical Analysis Reference Tissue Model [GARTM] [16], 4) a linearized version of the SRTM [SRTM_lin] [19], 5) a modification to the GARTM [GARTM_mod] [20], and 6) the “Basis Function Method” [BFM][21]. While a full derivation of these six models is outside of the scope of this article, a presentation of the key mathematical expressions converted to a dual–tracer nomenclature are provided below. The FRTM can be expressed as:

RO I T ( t )= R 1 [ RO I U ( t )+a⋅RO I U ( t )∗ e −ct +b⋅RO I U ( t )∗ e −dt ], with a=( k 3 + k 4 −c )⋅( c−r )/p b=( d− k 3 − k 4 )⋅( d−r )/p c=( s+p )/2 d=(s−p)/2   p= s 2 −q   q=4 k 2 k 4 r= k 2 / R 1 s= k 2 + k 3 + k 4 ∗= convolution integral,                                                                                                                                                  (1) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGsbGaam4taiaadMeadaWgaaWcbaGaamivaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaacqGH9aqpcaWGsbWaaSbaaSqaaiaaigdaaeqaaOWaamWaaeaacaWGsbGaam4taiaadMeadaWgaaWcbaGaamyvaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaacqGHRaWkcaWGHbGaeyyXICTaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaey4fIOIaamyzamaaCaaaleqabaGaeyOeI0Iaam4yaiaadshaaaGccqGHRaWkcaWGIbGaeyyXICTaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaey4fIOIaamyzamaaCaaaleqabaGaeyOeI0IaamizaiaadshaaaaakiaawUfacaGLDbaacaGGSaaabaaabaGaam4DaiaadMgacaWG0bGaamiAaiaaxMaacaWGHbGaeyypa0ZaaeWaaeaacaWGRbWaaSbaaSqaaiaaiodaaeqaaOGaey4kaSIaam4AamaaBaaaleaacaaI0aaabeaakiabgkHiTiaadogaaiaawIcacaGLPaaacqGHflY1daqadaqaaiaadogacqGHsislcaWGYbaacaGLOaGaayzkaaGaai4laiaadchaaeaacaWLjaGaamOyaiabg2da9maabmaabaGaamizaiabgkHiTiaadUgadaWgaaWcbaGaaG4maaqabaGccqGHsislcaWGRbWaaSbaaSqaaiaaisdaaeqaaaGccaGLOaGaayzkaaGaeyyXIC9aaeWaaeaacaWGKbGaeyOeI0IaamOCaaGaayjkaiaawMcaaiaac+cacaWGWbaabaGaaCzcaiaadogacqGH9aqpdaqadaqaaiaadohacqGHRaWkcaWGWbaacaGLOaGaayzkaaGaai4laiaaikdaaeaacaWLjaGaamizaiabg2da9iaacIcacaWGZbGaeyOeI0IaamiCaiaacMcacaGGVaGaaGOmaaqaaiaaykW7caWLjaGaamiCaiabg2da9maakaaabaGaam4CamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaadghaaSqabaaakeaacaaMc8UaaCzcaiaadghacqGH9aqpcaaI0aGaam4AamaaBaaaleaacaaIYaaabeaakiaadUgadaWgaaWcbaGaaGinaaqabaaakeaacaWLjaGaamOCaiabg2da9iaadUgadaWgaaWcbaGaaGOmaaqabaGccaGGVaGaamOuamaaBaaaleaacaaIXaaabeaaaOqaaiaaxMaacaWGZbGaeyypa0Jaam4AamaaBaaaleaacaaIYaaabeaakiabgUcaRiaadUgadaWgaaWcbaGaaG4maaqabaGccqGHRaWkcaWGRbWaaSbaaSqaaiaaisdaaeqaaaGcbaGaaCzcaiabgEHiQiabg2da9iaabccacaqGJbGaae4Baiaab6gacaqG2bGaae4BaiaabYgacaqG1bGaaeiDaiaabMgacaqGVbGaaeOBaiaabccacaqGPbGaaeOBaiaabshacaqGLbGaae4zaiaabkhacaqGHbGaaeiBaiaabYcacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabIcacaqGXaGaaeykaaaaaa@38B5@

Where ROIT(t) and ROIU(t) represent the measured uptake curves of the targeted and untargeted tracers, respectively, in any region of interest, as a function of time, t; R1 is the ratio of the rates of extravasation (K1) of the targeted tracer and the untargeted tracer; k2 is the rate of efflux of the targeted tracer; and k3 and k4 are the rates of association and dissociation of the targeted tracer, respectively (Figure 1).

Likewise, the SRTM can be expressed as:

RO I T ( t )= R 1 ⋅RO I U ( t )+ k 2 ( 1− R 1 1+BP )RO I U ( t )∗ e − k 2 1+BP t                                                  (2) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadsfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0JaamOuamaaBaaaleaacaaIXaaabeaakiabgwSixlaadkfacaWGpbGaamysamaaBaaaleaacaWGvbaabeaakmaabmaabaGaamiDaaGaayjkaiaawMcaaiabgUcaRiaadUgadaWgaaWcbaGaaGOmaaqabaGcdaqadaqaaiaaigdacqGHsisldaWcaaqaaiaadkfadaWgaaWcbaGaaGymaaqabaaakeaacaaIXaGaey4kaSIaamOqaiaadcfaaaaacaGLOaGaayzkaaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaey4fIOIaamyzamaaCaaaleqabaGaeyOeI0YaaSaaaeaacaWGRbWaaSbaaWqaaiaaikdaaeqaaaWcbaGaaGymaiabgUcaRiaadkeacaWGqbaaaiaadshaaaGccaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeikaiaabkdacaqGPaaaaa@8292@

Where BP, the “binding potential”, is equivalent to k3⁄k4, and is a key parameter since it represents the product of the receptor concentration (the parameter of interest) and the affinity of the targeted tracer for its receptor (which can in most cases be measured ex vivo) [13]. Going on, the format of the GARTM can be represented by:

∫ 0 t RO I T ( u )du RO I T ( t ) =( 1+BP ) ∫ 0 t RO I U ( u )du + RO I U ( t ) k 2 RO I T ( t ) +int,                                  (3) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaadaWdXbqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGubaabeaakmaabmaabaGaamyDaaGaayjkaiaawMcaaiaadsgacaWG1baaleaacaaIWaaabaGaamiDaaqdcqGHRiI8aaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadsfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaaaaiabg2da9maabmaabaGaaGymaiabgUcaRiaadkeacaWGqbaacaGLOaGaayzkaaWaaSaaaeaadaWdXbqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGvbaabeaakmaabmaabaGaamyDaaGaayjkaiaawMcaaiaadsgacaWG1baaleaacaaIWaaabaGaamiDaaqdcqGHRiI8aOGaey4kaSYaaSGaaeaacaWGsbGaam4taiaadMeadaWgaaWcbaGaamyvaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaaaeaacaWGRbWaaSbaaSqaaiaaikdaaeqaaaaaaOqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGubaabeaakmaabmaabaGaamiDaaGaayjkaiaawMcaaaaacqGHRaWkcaGGPbGaaiOBaiaacshacaGGSaGaaGPaVlaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabIcacaqGZaGaaeykaaaa@85FC@

Where u is a dummy time variable to integrate over, int is an often neglected intercept term in this linear relationship with slope 1+BP at time, t > t*, where t* represents the time it takes for the Cf and Cb to reach a constant ratio (quasi–equilibrium). The format of the SRTM_lin can be expressed as follows:

RO I T ( t )=[ R 1 ⋅RO I U ( t )+ k 2 ∫ 0 t RO I U ( u )du ]−( k 2 1+BP ) ∫ 0 t RO I T ( u )du .                               (4) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadsfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0ZaamWaaeaacaWGsbWaaSbaaSqaaiaaigdaaeqaaOGaeyyXICTaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaey4kaSIaam4AamaaBaaaleaacaaIYaaabeaakmaapehabaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG1baacaGLOaGaayzkaaGaamizaiaadwhaaSqaaiaaicdaaeaacaWG0baaniabgUIiYdaakiaawUfacaGLDbaacqGHsisldaqadaqaamaalaaabaGaam4AamaaBaaaleaacaaIYaaabeaaaOqaaiaaigdacqGHRaWkcaWGcbGaamiuaaaaaiaawIcacaGLPaaadaWdXbqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGubaabeaakmaabmaabaGaamyDaaGaayjkaiaawMcaaiaadsgacaWG1baaleaacaaIWaaabaGaamiDaaqdcqGHRiI8aOGaaiOlaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGOaGaaeinaiaabMcaaaa@821C@

Furthermore, the format of the GARTM_mod can be expressed as follows:

∫ 0 t RO I T ( u )du RO I U ( t ) =( 1+BP ) ∫ 0 t RO I U ( u )du RO I U ( t ) +int',                     (5) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaadaWdXbqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGubaabeaakmaabmaabaGaamyDaaGaayjkaiaawMcaaiaadsgacaWG1baaleaacaaIWaaabaGaamiDaaqdcqGHRiI8aaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaaaaiabg2da9maabmaabaGaaGymaiabgUcaRiaadkeacaWGqbaacaGLOaGaayzkaaWaaSaaaeaadaWdXbqaaiaadkfacaWGpbGaamysamaaBaaaleaacaWGvbaabeaakmaabmaabaGaamyDaaGaayjkaiaawMcaaiaadsgacaWG1baaleaacaaIWaaabaGaamiDaaqdcqGHRiI8aaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaaaaiabgUcaRiaacMgacaGGUbGaaiiDaiaacEcacaGGSaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeikaiaabwdacaqGPaaaaa@749B@

Where int’ represents another neglected intercept that is different in composition than the one in Equation (3).

Finally, Gunn’s Basis Function Method (BFM) is derived from Equation (2) and is formulated as:

RO I T (t)= θ 1 RO I U (t)+ θ 2 B i (t)        (6) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadsfaaeqaaOGaaiikaiaadshacaGGPaGaeyypa0JaeqiUde3aaSbaaSqaaiaaigdaaeqaaOGaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOGaaiikaiaadshacaGGPaGaey4kaSIaeqiUde3aaSbaaSqaaiaaikdaaeqaaOGaamOqamaaBaaaleaacaWGPbaabeaakiaacIcacaWG0bGaaiykaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeikaiaabAdacaqGPaaaaa@5443@

whereθ1= R1, Θ2 = k2– R1k2/(1+BP), Bi are the so–called basis functions defined as:

Bi(t)=RO I U (t)⊗ e − θ 3,i t        (7) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaSGaamyAaOGaaiikaiaadshacaGGPaGaeyypa0JaamOuaiaad+eacaWGjbWaaSbaaSqaaiaadwfaaeqaaOGaaiikaiaadshacaGGPaGaey4LIqSaamyzamaaCaaaleqabaGaeyOeI0IaeqiUde3aaSbaaWqaaiaaiodacaGGSaGaamyAaaqabaWccaWG0baaaOGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabIcacaqG3aGaaeykaaaa@50CE@

andθ3 = k2/(1+BP); so that Equation (6) can be optimized for θ1and θ2 in a linear least squares sense; provided that θ3 is varied iteratively over a specified range.

Materials and Methods

Animal experiments

Targeted and untargeted tracer uptake curves were measured in two different tumor lines grown subcutaneously in athymic mice (n = 10, Charles River, Wilmington, MA). The targeted tracer was a ligand for the Epidermal Growth Factor Receptor (EGFR), a receptor that is over expressed in many cancers [22]. Specifically, the tracer was a near–infrared fluorescent molecule bound to native epidermal growth factor, IRDye–800CW–EGF (LI–COR Biosciences, Lincoln, NE). The untargeted tracer was a free near–infrared fluorescent tracer emitting fluorescence at a separate wavelength, IRDye–700DX carboxylate (LI–COR Biosciences). The two different tumor lines were selected so as to represent different levels of Epidermal Growth Factor Receptor (EGFR) and were each implanted into five of the ten immune–deficient mice (Charles River, Wilmington, MA). Five mice were inoculated with a human neuronal glioblastoma (U251; supplied from Dr. Mark Israel, Norris Cotton Cancer Center, Dartmouth–Hitchcock Medical Center), a cancer cell line known to express moderate levels of EGFR [23,24]; and another five mice were inoculated with a human epidermoid carcinoma (A431; ATCC, Manassas, VA), known to express a very large amount of EGFR [25]. In all cases, the tumors were introduced by injecting 1x106 tumor cells in Matrigel ®(BD Biosciences, San Jose, CA) into the subcutaneous space on the left thigh of the mice. The tumors were then allowed to grow to a size of approximately 150 mm3 before imaging.

The mice were anesthetized with ketamine–xylazine (100 mg⁄kg: 10 mg⁄kg i.p.) and the superficial tissue surrounding the tumors was removed. Each mouse was then placed tumor–side down on a glass slide and loosely secured with surgical tape (Figure 1). Once plated, the mice were positioned onto the imaging plane of an Odyssey Scanner (LI–COR Biosciences, Lincoln, NE). The Odyssey Scanner employs raster scanning and two lasers (one emitting at 685 nm and another at 785 nm) to excite two fluorophores simultaneously, pixel–by–pixel, and utilizes a series of dichroic mirrors to decouple fluorescence from the LI–COR 680 or 700 nm fluorescent tracers and the LI–COR 800 nm fluorescent tracer, respectively. All mice were injected with a cocktail of 1 nanomole of an EGFR targeted fluorescent tracer and 1 nanomole of an untargeted fluorescent tracer: the untargeted tracer was a carboxylate form of the IR Dye 700DX NHS Ester (LI–COR Biosciences, Lincoln, NE) that was reacted with water for 3h at room temperature to convert the reactive NHS Ester to a non–reactive carboxylate (as per manufacturer’s instructions to reduce nonspecific binding), and the targeted tracer was IR Dye 800CW–EGF (LI–COR Biosciences, Lincoln, NE). The mice were then imaged at approximately 3–min intervals for 1h after injection of the fluorescent tracers.

Figure 1: A photograph of the dual-tracer experimental setup of a U251 mouse with tumor exposed is presented in (a): targeted tracer (red) and untargeted tracer (green) fluorescence uptake images at 60 min post-tracer injection are presented in (b). The tumor area has been marked by the dashed rectangle (b), and the corresponding compartment models (c). ROIT(t) and ROIU(t) represent the measured uptake curves of the targeted and untargeted tracers, respectively, in any region of interest, as a function of time, t; vp is the blood volume percentage in the tumor; K1 and k2 are the rates of exchange of the tracers from the blood concentration (Cp) to the interstitial space (Cf for the targeted tracer and CU for the untargeted tracer) and back, respectively; and k3 and k4 are the rates of association and dissociation of the targeted tracer to its receptor in a bound state (Cb). Typical uptake curves of the targeted tracer (red) and the untargeted tracer (blue) in a single pixel in a low signal-to-noise scenario is presented in (e). The smooth “fits” are polynomials fit to the data to determine the noise characteristics.






Figure 1:  A photograph of the dual-tracer experimental setup of a U251 mouse with tumor exposed is presented in (a): targeted tracer (red) and untargeted tracer (green) fluorescence uptake images at 60 min post-tracer injection are presented in (b). The tumor area has been marked by the dashed rectangle (b), and the corresponding compartment models (c). ROIT(t) and ROIU(t) represent the measured uptake curves of the targeted and untargeted tracers, respectively, in any region of interest, as a function of time, t; vp is the blood volume percentage in the tumor; K1 and k2 are the rates of exchange of the tracers from the blood concentration (Cp) to the interstitial space (Cf for the targeted tracer and CU for the untargeted tracer) and back, respectively; and k3 and k4 are the rates of association and dissociation of the targeted tracer to its receptor in a bound state (Cb). Typical uptake curves of the targeted tracer (red) and the untargeted tracer (blue) in a single pixel in a low signal-to-noise scenario is presented in (e). The smooth “fits” are polynomials fit to the data to determine the noise characteristics.

Image analysis

The first step in the image analysis was to remove autofluorescence (background fluorescence from the datasets. This was done by subtracting a pre–injection image of targeted and untargeted tracer channel fluorescence from all subsequent post–injection images [26]. Next, the potential differences in detection efficiency at the two wavelengths were normalized by taking the ratio of measured fluorescence from the targeted and untargeted tracers in a region of interest devoid of targeted receptor, and multiplying this “normalization” factor with all uptake images [12]. A pixelwise fitting procedure was then performed according to each of the six aforementioned models in the tumor and surrounding tissues to calculate parametric maps of binding potential (which for the targeted tracer employed, is equivalent to EGFR concentration in units of nM because the affinity of EGF for EGFR is 1 nM–1[27] and receptor concentration is equivalent to the product of the binding potential and the tracer affinity [13]). In the case of the FRTM, SRTM, and SRTM_lin models, their use was additionally tested when holding the parameter R1 = 1, since it is the ratio of K1s of the targeted and untargeted tracers, which should be equivalent[14]. MATLAB (Natick, MA) was used for all curve fitting procedures and the built in function lsqcurvfit() was used for non–linear fitting (FRTM & SRTM), while polyfit() was used for the GARTM and GARTM_mod models, and the back–slash operator was used for SRTM_lin model. For the BFM model, the simulation was performed using both the conventional QR decomposition approach [21]and the back–slash operator. All curves were interpolated to 0.1 min temporal resolution using interp1() with a spline approach prior to the use of convolution or integration algorithms in MATLAB to avoid discretization errors.

Simulated data

As an initial test of the six models described in the Theory, targeted and untargeted tracer uptake curves were simulated for a typical level of EGFR expression in a moderate expressing tumor (2 nM [12]). The targeted tracer uptake curve was simulated based on a full solution to the two–tissue compartment model depicted in Figure 1 – that can be found in Appendix A of Lammertsma et al. [18] and the untargeted tracer uptake curve was simulated based on a one–tissue compartment model, also known as the Kety model [28]. Each of these model–types requires a plasma input function, i.e., the concentration of the tracer in the blood over time, which was chosen from blood sampling experiments published previously [29] that were carried out in a cohort of 13 mice using the same targeted and untargeted tracers used in the current study. Furthermore, the rate constants K1– k4 needed to be assumed. For the purposes of the simulations here we assumed that the untargeted tracer was an ideal pair for the targeted tracer and therefore K1 and k2 were assumed to be equivalent between the tracers. Values of K1 and k2 were chosen based on the work of de Lussanet et al. who evaluated these parameters in tumors for different sized contrast agents; values associated with the 3.0–kDa agent were chosen as it most closely matched the size of the targeted tracer employed in the animal experiments (˜ 7 kDa): the values were K1 = 0.013 min–1 and k2 = 0.13 min–1[30]. The disassociation binding rate constant k4 is equivalent to koff in enzyme kinetic nomenclature and was measured by Zhou et al. to be approximately 0.1 min–1 for EGF bound to EGFR [27] – native EGF was the targeting moiety used in the animal experiments in this study. Then with binding potentials (k3⁄ k4) roughly equivalent to 2 for a typical EGFR overexpressing tumor line (U251: see Animal experiments), k3 was by association assumed to be equal to 0.2 min–1. The binding rates would be equivalent to a 2 nM concentration of EGFR using a native EGF based targeted tracer. All simulated targeted and untargeted tracer uptake curves were interpolated to 1–minute interval time–points from 1 to 60 min after tracer injection.

To best represent the actual animal data, a pixel–wise noise detection technique was performed to approximate the noise variance (percentage) in the Odyssey Scanner images. At each pixel, the targeted and untargeted uptake curves at all time points were extracted and fitted to a fifth–order polynomial [Figure 1(d)]. The standard deviation of the error between the fit and the actual curves was averaged over all pixels in a region of interest and normalized by the maximum value of the curves to represent an overall measure of noise in that region. It was noticed that the noise metric was generally less in the untargeted uptake curves compared to the targeted ones but, without loss of generality, this fact was not incorporated in the simulations. In most cases (for different images and different regions of interest), the average noise did not exceed 3% of the signal; therefore, 3% Gaussian noise was added to all simulated tracer uptake curves prior to employing the kinetic models described in the Theory to back–out the simulated EGFR concentration.

Results and Discussion

Animal experiments

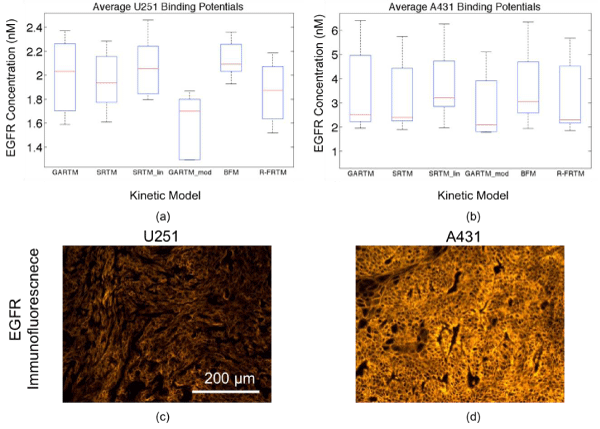
Figure 2 presents the average EGFR concentrations measured using all models described in the Theory. All of the models produced very similar results with the spread in averages being about 25% of the mean. There were no statistically significant differences between the results of any of the models except for the GARTM_mod, which produced significantly lower estimates of EGFR than all other models in both tumor groups (n = 5 in each tumor group, p> 0.05).It should be noted here that reference tissue approaches have been applied to similar data in a past study resulting in greater than 50% errors in EGFR concentration estimation [13]. These results highlight the necessity of utilizing dual–tracer methods, despite the added expense and inconvenience, because single tracer approaches are simply unsuitable for tumor imaging studies.

Figure 2: Box plots of epidermal growth factor (EGFR) concentration estimates from all models are presented in (a) for the human glioma xenograft mice (U251 cell line) and in (b) for the human epidermoid xenograft mice (A431 cell line). The kinetic models are the graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM). The red lines represent the median EGFR concentration estimates. Example EGFR immunofluorescence stains of ex vivo U251 and A431 tumor tissue excised from the mice are presented in (c) and (d), respectively, presented on the same fluorescence scale.






Figure 2:  Box plots of epidermal growth factor (EGFR) concentration estimates from all models are presented in (a) for the human glioma xenograft mice (U251 cell line) and in (b) for the human epidermoid xenograft mice (A431 cell line). The kinetic models are the graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM). The red lines represent the median EGFR concentration estimates. Example EGFR immunofluorescence stains of ex vivo U251 and A431 tumor tissue excised from the mice are presented in (c) and (d), respectively, presented on the same fluorescence scale.

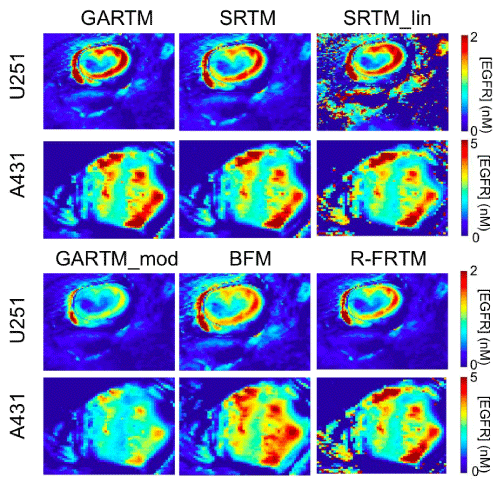
Figure 3 presents parametric maps from one typical U251 mouse and one A431 mouse for each of the tested kinetic models. On the whole, the visual quality (in terms of pixel fitting robustness to noise) of the parametric maps was adequate and comparable between models. Only the SRTM_lin model appeared to suffer from some instability. Upon noise analysis (Figure 4), it did not appear than the instability in EGFR concentration estimation of the SRTM_lin resulted from a heightened sensitivity to noise. Rather, it appears as if the model becomes unstable in tissues with very little targeted tracer binding. The current implementation of SRTM_lin in this paper utilizes a “back–slash” operation in MATLAB; however, future applications could include iterative fitting routines that would slow the algorithm down, but would allow constraints to be enacted that could improve the stability.

Figure 3: Parametric maps of estimated epidermal growth factor receptor (EGFR) concentration. The SRTM_lin model lacks constraints and thus fails to produce maps as ‘clean’ as those generated by other models; as seen from the holes and saturated values in the maps on the top right of the figure.






Figure 3:  Parametric maps of estimated epidermal growth factor receptor (EGFR) concentration. The SRTM_lin model lacks constraints and thus fails to produce maps as ‘clean’ as those generated by other models; as seen from the holes and saturated values in the maps on the top right of the figure.

There are no quantitative gold standard methods for measuring in vivo receptor concentrations, so it is difficult to determine whether the GARTM_mod of the other models were more accurate from the experimental data alone. In a separate study, ex–vivo rough estimates of EGFR concentration in the U251 tumors and A431 tumors were 1.6 ± 0.4 and 2.7 ± 0.4 nM, respectively [12], suggesting perhaps that the GARTM_mod would be most accurate, but the rough estimates should not be held as quantitative and therefore cannot be used to make any conclusions other than supporting the fact that the A431 expresses significantly more EGFR than the U251 tumors (a trend strongly supported by all models). In a separate cohort of 12 mice (6 U251, 6 A431), ex vivo analysis was carried out to determine a relative estimate of in vivo EGFR concentration using EGFRlabelled immunofluorescence [Fig. 2(c) and (d)]. The relative value of immunofluorescence for U251 tumors was 2.5 ± 0.1, while A431 was 7.2 ± 0.9. These values correlated well with the dualtracer methodology measured average in vivo estimates of EGFR concentration, which were 1.9 ± 0.3 and 3.8 ± 1.0 nM for U251 and A431, respectively, averaging all models (assuming zero intercept: p< 0.05, r = 0.98 for correlation). In addition to this ex vivo analysis, a number of simulation studies were carried out to better evaluate the accuracy and precision of the various kinetic models.

Table 1: Comparison of the models in terms of accuracy and speed. The first and third rows show the means and standard deviation (sd) of the graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM) for the medium sized particle simulations. The fourth row represents the time taken for the models to perform the fit for 10000 iterations. These results and their interpretations may vary for different particles and computers.




  

    
 

      
 

    
GARTM 

    
SRTM 

    
SRTM_lin 

    
BFM 

    
R-FRTM 

    
GARTM_mod 

  

  

    
Estimated Receptor Concentration� (Mean � SD) 

    
1.9 � 0.1

    
2.0 � 0.1

    
2.1 � 0.1

    
1.9 � 0.0

    
2.1 � 0.1

    
1.1 � 0.0

  

  

    
Error in receptor concentration estimate 

    
-0.06

    
0.04

    
0.06

    
-0.12

    
0.08

    
-0.89

  

  

    
Elapsed Time for 10,000 fits (s) 

    
13

    
240

    
5

    
103

    
838

    
25

  









Table 1:   Comparison of the models in terms of accuracy and speed. The first and third rows show the means and standard deviation (sd) of the graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM) for the medium sized particle simulations. The fourth row represents the time taken for the models to perform the fit for 10000 iterations. These results and their interpretations may vary for different particles and computers.

Simulated data

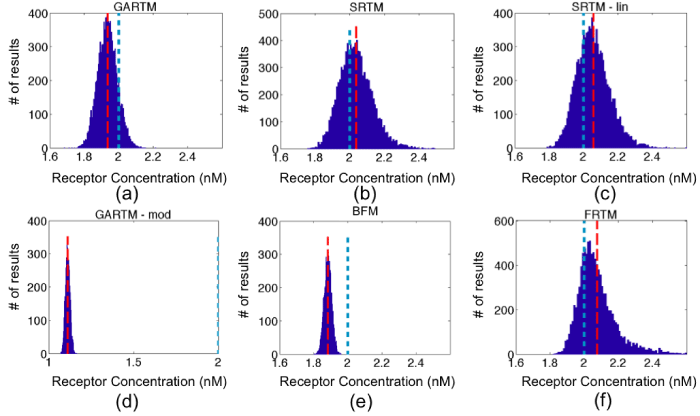
Figure 4 and 5 present the results of the simulation studies described in the Methods, with numerical results of accuracy, precision and computational cost, summarized in Table 1. The SRTM, SRTM_lin, and reduced FRTM results all provided the most accurate results, with the BFM and GARTM slightly underestimating the simulated level of receptor concentration, and the GARTM_mod, strongly underestimating the simulated receptor concentration. The fact that GARTM_mod does not work for our case was expected, since according to the authors of the approach, it has been developed for the special case of PET imaging in rats and is not guaranteed to work in other frameworks [20]. Interestingly though, in a comparative sense, the GARTM_mod appeared to be fair much better in the animal experiments than in simulations, and could be considered a viable model owing to its computational efficiency and the fact that it does not require an estimate of k2 like the GARTM.

Figure 4: Fitting receptor concentration results from applying the six models [graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM)] – (a)-(f), respectively – to simulated curves with additive Gaussian noise of 3% for 10,000 iterations. The red dashed and the blue dotted vertical lines indicate the positions of the means of the fit and the true BP respectively. The scales for horizontal axes are the same in all figures except GARTM_mod, which produced out of bound values for Binding Potential.






Figure 4:  Fitting receptor concentration results from applying the six models [graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM)] – (a)-(f), respectively – to simulated curves with additive Gaussian noise of 3% for 10,000 iterations. The red dashed and the blue dotted vertical lines indicate the positions of the means of the fit and the true BP respectively. The scales for horizontal axes are the same in all figures except GARTM_mod, which produced out of bound values for Binding Potential.

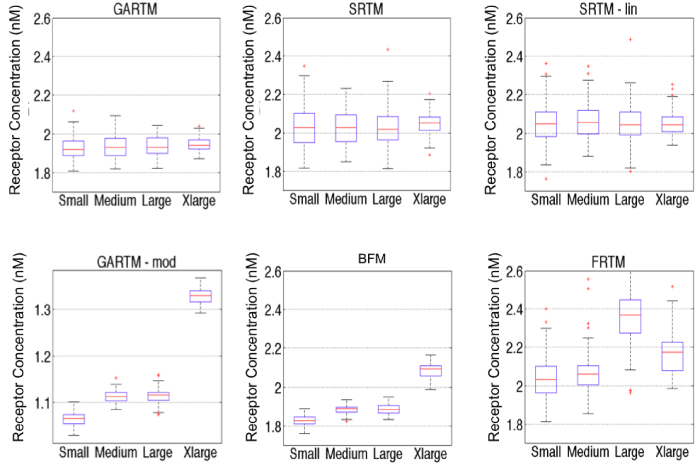
Figure 5: Comparison of fitting performances of different models [graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM)] and different particles within each model. Fitting is done for 100 times for each particle within each model. Note: the red data are outliers of the data distributions.






Figure 5:  Comparison of fitting performances of different models [graphical analysis reference tissue model (GARTM), the simplified reference tissue model (SRTM), the linearized-SRTM (SRTM_lin), a modified GARTM (GARTM_mod), a basis function model (BFM), and a “reduced” full reference tissue model (R-FRTM)] and different particles within each model. Fitting is done for 100 times for each particle within each model. Note: the red data are outliers of the data distributions.

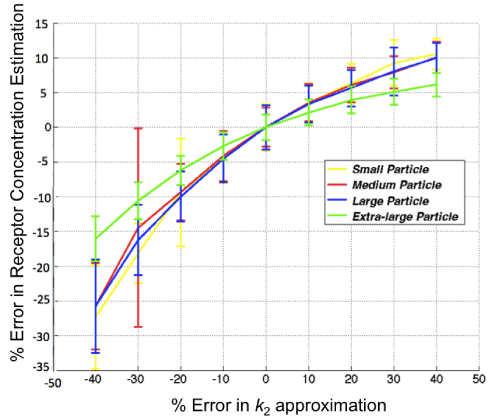
With respect to the GARTM, the slight underestimation in receptor concentration estimation is a well–known phenomenon of the model attributable to a noise bias [31]; however, it should be noted that novel adaptations of the GARTM have been developed to account for this noise bias [32]. The fact that such an underestimation was not observed in the animal experiments compared to the SRTM based models could have stemmed from an overestimation in the assumed value of k1 (which was assumed to be 0.1 min–1 in the animal experiments). Figure 6 presents a sensitivity profile of the error in receptor concentration estimation using GARTM given errors in assumed k2 for tracers of different sizes from small to x–large, using K1 and k2 parameters from de Lussanet et al. as a reference [30]. Theslight underestimation in receptor concentration of the BFM was found to be attributable to the fit constraints, which are effectively realized in the pre–specified range for Θ3.In fact, the BFM could perhaps be considered the best overall model if it weren’t for the known sensitivity in estimations to the parameters of the fit [21]. The model is nearly as fast as SRTM_lin, more stable in low binding tissues, and can have excellent accuracy and precision; although its sensitivity to the constraints, especially to the lower bound of the Θ3 range, is such that a 1 percent change in the lower bound could sometimes yield a 20 percent change in the estimated BP value.

Figure 6: Sensitivity of the results of the graphical analysis reference tissue model (GARTM) to errors in the value of k2. The true k2 is 0.13 in this case and the noise added to the curves is 3%.






Figure 6:  Sensitivity of the results of the graphical analysis reference tissue model (GARTM) to errors in the value of k2. The true k2 is 0.13 in this case and the noise added to the curves is 3%.

All figures do not include results from the FRTM because fits using this model resulted in largely spurious estimates of EGFR concentration estimates of –0.03 and –0.05 for the U251 and A431 tumor groups, respectively. It may just be that the model requires careful consideration of starting parameters and constraints in the fitting; however, the fourth degree of freedom is known to be problematic, which is why this model is rarely used in reference tissue modelling [15].The “reduced” FRTM, however, wherein R1 was set equal to 1 to reduce the number of fitting parameters to three (a constraint only possible in dual–tracer imaging and not possible in reference tissue modelling), produced promising results. According to this finding, it was presumed that a similar constraint (setting R1=1) would also improve the characteristics of the SRTM and SRTM_lin; however, these new “two–parameter” models were tested both in simulation and on the animal data, where they were found to be very unstable. Presumably, this is because including R1 as a fitting parameter provides a necessary degree of freedom to deal with small differences in scale between the targeted and untargeted tracer uptake curves that was unnecessary in the reduced FRTM (i.e., fitting for R1 can help account for any bias caused by noise or imprecise detector efficiency normalization, while setting it to 1 causes other parameters to suffer from the bias in a more unstable manner).

One very interesting potential advantage of the reduced–FRTM that requires future study, is that it is the only model that does not make an assumption of an instantaneous equilibrium between the free and bound concentrations of targeted tracer in its compartment model (the so–called “adiabatic approximation” [15]): see Fig. 1(c). The binding kinetics of EGF [27], the targeting ligand employed in the animal experiments in this study, and the similar levels of k3 and k4 employed in the simulations, appear to support the adiabatic approximation; however, larger, more specific targeting moieties may have slower binding kinetics that would preclude validity of the approximation [33]. It is for these applications that the reduced– FRTM could have a unique advantage.

Some other less substantial findings warrant some discussion. It was found that the specification of upper and lower bounds for models using the built–in function lsqcurvefit() was an issue that needed to be dealt with carefully. Without specifying the proper bounds, SRTM and the Reduced FRTM tended to produce out of bound or ‘saturated’ values for EGFR concentration at some pixels in the animal experiment results (presumably owing to noise and the abnormal behaviour of the targeted and untargeted curves at those pixels). Cselenyi et al. have set these outlier values to zero in their algorithm, thus getting binding potential maps that contain ‘holes’ [34]. In this study, the fitting procedure was constrained instead, by manually altering the constraints until achieving the optimum results and a ‘‘clean’ parametric map. Future work is on–going to determine a more automated approach for selecting the parameters of the fit.

In terms of speed, the SRTM_lin model was the fastest and the Reduced FRTM the slowest. SRTM was about 10 times slower than GARTM and BFM, but not necessarily more efficient. For SRTM and Reduced FRTM, MATLAB’s lsqcurvefit() function was used to incorporate constraints on fitted values; otherwise the models would overload for some experimental cases. The employment of lsqcurvefit() in these models had two effects: first, it slowed down the optimization algorithm (SRTM_lin is the fastest because it does not use such constraints and performs the fit with a simple back–slash operator); second, the constraints need to be manually selected for each case to avoid out of bound values for fit parameters. It would be worthwhile to employ other optimization toolboxes for these two models to both speed them up and also automate the process of finding their constraints. The Reduced FRTM could also be linearized in a similar manner as SRTM_lin for increased speed. This is left for future studies.

Conclusion

A reduced version of the full two–compartment kinetic model, along with five other prevalent kinetic modelling approaches used widely in tracer kinetics nomenclature were studied, implemented, and evaluated in this study; with particular emphasis on employment of these models in a dual–tracer modeling framework. Evaluation was carried out in EGFR targeted studies in experimental mouse tumor xenograft models, and was supported by theoretical simulations. In general, no single model outperformed the others for dual–tracer modeling; instead, each model came with their own strengths and weaknesses. Overall, the reduced FRTM, SRTM, and SRTM_lin models provided the most accurate estimates of binding potential in simulations and experimental results; however, they did result in larger variation to noise compared to GARTM and the Gunn approaches. One potential advantage of the reduced FRTM is that it is the only model that does not assume an instantaneous equilibrium between the bound and free compartments of the targeted tracer model. Future work will explore the potential advantages of this model for estimating binding kinetics of larger targeting moieties such as antibodies that may not obey this assumption [33]. If the instantaneous equilibrium assumption is valid, the SRTM_lin model could be argued to provide a good balance of advantages. It was considerably faster than all other models except for GARTM, it does not require an estimate of k2 (as is the case with GARTM), and it provided the most accurate results in simulations.

Acknowledgements

This research was funded by NIH grants P01CA084203, R01CA156177 and U54CA151662. K. M. T. and J. T. E. acknowledge funding from the CIHR postdoctoral fellowship program. We would also like to thank Kristian J. Sexton and Harold H. Yang for their assistance with running the animal experiments.

References

  1. Arrowsmith J. Trial watch: Phase II failures: 2008-2010. Nat Rev Drug Discov. 2011; 10: 328-329.
  2. Arrowsmith J. Trial watch: phase III and submission failures: 2007-2010. Nat Rev Drug Discov. 2011; 10: 87.
  3. Sawyers C. Targeted cancer therapy. Nature. 2004; 432: 294-297.
  4. Weissleder R, Pittet MJ. Imaging in the era of molecular oncology. Nature. 2008; 452: 580-589.
  5. Jain RK. Physiological barriers to delivery of monoclonal antibodies and other macromolecules in tumors. Cancer Res. 1990; 50: 814s-819s.
  6. Jain RK. Vascular and interstitial barriers to delivery of therapeutic agents in tumors. Cancer Metastasis Rev. 1990; 9: 253-266.
  7. Maeda H, Wu J, Sawa T, Matsumura Y, Hori K. Tumor vascular permeability and the EPR effect in macromolecular therapeutics: a review. J Control Release. 2000; 65: 271-284.
  8. Wang D, Chen Y, Leigh SY, Haeberle H, Contag CH, Liu JT. Microscopic Delineation of Medulloblastoma Margins in a Transgenic Mouse Model Using a Topically Applied VEGFR-1 Probe. Transl Oncol. 2012; 5: 408-414.
  9. Pogue BW, Samkoe KS, Hextrum S, O'Hara JA, Jermyn M, Srinivasan S, et al. Imaging targeted-agent binding in vivo with two probes. J Biomed Opt. 2010; 15: 030513.
  10. Liu JT, Helms MW, Mandella MJ, Crawford JM, Kino GS, Contag CH. Quantifying cell-surface biomarker expression in thick tissues with ratiometric three-dimensional microscopy. Biophys J. 2009; 96: 2405-2414.
  11. Baeten J, Haller J, Shih H, Ntziachristos V. In vivo investigation of breast cancer progression by use of an internal control. Neoplasia. 2009; 11: 220-227.
  12. Tichauer KM, Samkoe KS, Sexton KJ, Hextrum SK, Yang HH, Klubben WS, et al. In vivo quantification of tumor receptor binding potential with dual-reporter molecular imaging. Mol Imaging Biol. 2012; 14: 584-592.
  13. Innis RB, Cunningham VJ, Delforge J, Fujita M, Gjedde A, Gunn RN, et al. Consensus nomenclature for in vivo imaging of reversibly binding radioligands. J Cereb Blood Flow Metab. 2007; 27: 1533-1539.
  14. Tichauer KM, Samkoe KS, Klubben WS, Hasan T, Pogue BW. Advantages of a dual-tracer model over reference tissue models for binding potential measurement in tumors. Phys Med Biol. 2012; 57: 6647-6659.
  15. Lammertsma AA, Hume SP. Simplified reference tissue model for PET receptor studies. Neuroimage. 1996; 4: 153-158.
  16. Logan J, Fowler JS, Volkow ND, Wang GJ, Ding YS, Alexoff DL. Distribution volume ratios without blood sampling from graphical analysis of PET data. J Cereb Blood Flow Metab. 1996; 16: 834-840.
  17. Hume SP, Myers R, Bloomfield PM, Opacka-Juffry J, Cremer JE, Ahier RG, et al. Quantitation of carbon-11-labeled raclopride in rat striatum using positron emission tomography. Synapse. 1992; 12: 47-54.
  18. Lammertsma AA, Bench CJ, Hume SP, Osman S, Gunn K, Brooks DJ, et al. Comparison of methods for analysis of clinical [11C]raclopride studies. J Cereb Blood Flow Metab. 1996; 16: 42-52.
  19. Ichise M, Toyama H, Innis RB, Carson RE. Strategies to improve neuroreceptor parameter estimation by linear regression analysis. J Cereb Blood Flow Metab. 2002; 22: 1271-1281.
  20. Topping GJ, Dinelle K, Kornelsen R, McCormick S, Holden JE, Sossi V. Positron emission tomography kinetic modeling algorithms for small animal dopaminergic system imaging. Synapse. 2010; 64: 200-208.
  21. Gunn RN, Lammertsma AA, Hume SP, Cunningham VJ. Parametric imaging of ligand-receptor binding in PET using a simplified reference region model. Neuroimage. 1997; 6: 279-287.
  22. Nicholson RI, Gee JM, Harper ME. EGFR and cancer prognosis. Eur J Cancer. 2001; 37: S9-15.
  23. Gibbs-Strauss SL, Samkoe KS, O'Hara JA, Davis SC, Hoopes PJ, Hasan T, et al. Detecting epidermal growth factor receptor tumor activity in vivo during cetuximab therapy of murine gliomas. Academic radiology. 2010; 17: 7-17.
  24. Smith JJ, Derynck R, Korc M. Production of transforming growth factor alpha in human pancreatic cancer cells: evidence for a superagonist autocrine cycle. Proceedings of the National Academy of Sciences of the United States of America. 1987; 84: 7567-7570.
  25. Wikstrand CJ, McLendon RE, Friedman AH, Bigner DD. Cell surface localization and density of the tumor-associated variant of the epidermal growth factor receptor, EGFRvIII. Cancer research. 1997; 57: 4130-4140.
  26. Samkoe KS, Sexton K, Tichauer KM, Hextrum SK, Pardesi O, Davis SC, et al. High vascular delivery of EGF, but low receptor binding rate is observed in AsPC-1 tumors as compared to normal pancreas. Mol Imaging Biol. 2012; 14: 472-479.
  27. Zhou M, Felder S, Rubinstein M, Hurwitz DR, Ullrich A, Lax I, et al. Real-time measurements of kinetics of EGF binding to soluble EGF receptor monomers and dimers support the dimerization model for receptor activation. Biochemistry. 1993; 32: 8193-8198.
  28. Kety SS. The theory and applications of the exchange of inert gas at the lungs and tissues. Pharmacol Rev. 1951; 3: 1-41.
  29. Tichauer KM, Samkoe KS, Sexton KJ, Gunn JR, Hasan T, Pogue BW. Improved tumor contrast achieved by single time point dual-reporter fluorescence imaging. J Biomed Opt. 2012; 17: 066001.
  30. de Lussanet QG, Langereis S, Beets-Tan RG, van Genderen MH, Griffioen AW, van Engelshoven JM, et al. Dynamic contrast-enhanced MR imaging kinetic parameters and molecular weight of dendritic contrast agents in tumor angiogenesis in mice. Radiology. 2005; 235: 65-72.
  31. Logan J, Fowler JS, Volkow ND, Ding YS, Wang GJ, Alexoff DL. A strategy for removing the bias in the graphical analysis method. J Cereb Blood Flow Metab. 2001; 21: 307-320.
  32. Logan J, Alexoff D, Fowler JS. The use of alternative forms of graphical analysis to balance bias and precision in PET images. J Cereb Blood Flow Metab. 2011; 31: 535-546.
  33. Thurber GM, Dane Wittrup K. A mechanistic compartmental model for total antibody uptake in tumors. J Theor Biol. 2012; 314: 57-68.
  34. Cselényi Z, Olsson H, Halldin C, Gulyés B, Farde L. A comparison of recent parametric neuroreceptor mapping approaches based on measurements with the high affinity PET radioligands [11C]FLB 457 and [11C]WAY 100635. Neuroimage. 2006; 32: 1690-1708.

Citation: Hamzei N, Samkoe KS, Elliott JT, Holt RW, Tichauer KM et al. Comparison of Kinetic Models for Dual- Tracer Receptor Concentration Imaging in Tumors. Austin J Biomed Eng. 2014;1(1): 1002. ISSN: 2381-9081.