Bayesian Models for Healthcare Data Analysis

Xiaoshan Xie¹*, Gang Zhang¹, Ying Huang¹ and Shanxing Ou²*

¹School of Automation, Guangdong University of Technology, China

²Department of Radiology, Guangzhou General Hospital of Guangzhou Military Command, China

*Corresponding author: :Xiaoshan Xie, School of Automation, Guangdong University of Technology, Guangzhou, 510006, China.

Received: May 15, 2014; Accepted: June 16, 2014; Published: June 18, 2014

Abstract

The rapid increasing amount of healthcare data poses great challenges to data mining and machine learning study and applications. Recently a large number of algorithms and models have been proposed to discover knowledge and information from large scale healthcare datasets. In medical applications, confidence measured by posterior probability is well accepted since it can quantify the certainty or severity of targets. In this article, we propose a sparse Bayesian model for healthcare data analysis. The proposed model utilizes a set of basic functions and it learns a sparse weight vector to combine them together. Our model is a fully Bayesian method which can incoporate a prior and derive a likelihood function from a given training data set. Working with the images of Pulmonary Embolism diagnosis dataset and Breast Cancer clinical dataset from KDDCup, our experiments demonstrate that the Bayesian approach lead to 83% and 80% test accuracy in modeling principles of healthcare data and it significantly improves the performance of its couterparts.

Introduction

With the increasing availability of biomedical and healthcare data with a wide range of sophisticated characteristics, healthcare data analysis has been an popular and challenging work in recent years. Therefore, a large number of algorithms in data mining have been proposed to model the uncertainties that come with the problem, including Decision Tree (DT), Neural Network (NN), Bayesian methods, association rule mining and so on. Currently, benefit from natural advantages of mining and learning in recognizing significant facts, relationships, trends and anomalies, mining and learning techniques have been widely applied in healthcare domain [1,2]. As early as 1997, to improve the quality of care as well as to help control spiraling costs in healthcare industry, Rogers et al. [3] applied the SAS technology to solve critical bussiness solutions with the healthcare industry. Moreover, Sellappan et al. [4] developed a web-based Intelligent Heart Disease Prediction System (IHDPS) by using Decision trees, Naive Bayes and Neural Network, which was considered as one of a prominent model [5]. And it also can be implemented to better understand key indicators involving quality outcomes and encounters of care. Liu Peng et al. [6] proposed to utilize decision tree, Naive Bayesian classifiers and feature selection methods to predict inpatient length of stay. A PSO-SVM based on association rules in automatic detection of erthemato-squamous diseases obtain higher accuracy [7,8]. And detection of fraudulent insurance claims, making better health policy, forecasting treatment costs are also applications of data mining in healthcare domain [9,10]. Nevertheness, according to the survey of [11], few data mining methods are treated as practically valuable tools for clinical purposes. To better solve these issues, Bayesian method has been attached more importance in theorical study and some new algorithms based on it have been proposed to solve practical problems.

Bayesian method is the powerful one that emerges as a method for discovering patterns in biomedical data and has better speed and accuracy for huge datasets [8,12,13]. Naive Bayesian Classifier (NBC) uses probability to represent each class and trends to find the most possible class for each sample, which always performs well in practice [6]. And the Naive Bayesian Imputation (NBI) proposed in [14] is used for missing data handling. Zhao et al. [15] proposed a Bayesian-based Personalized Laboratory Test prediction (BPLT) to predict laboratory tests for a given group of patients. By considering the aquisition of data from different sources, Martijin described a new formalism named multilevel Bayesian networks for the analysis of hierarchical health care data [16].

In this article, we attempt to construct a sparse model based on Bayesian learning methods. The proposed method tries to model the generative principles of the target data set. Mathematically, we often express a generative model as following:

y = w^{t} Φ (x) + ε (1)

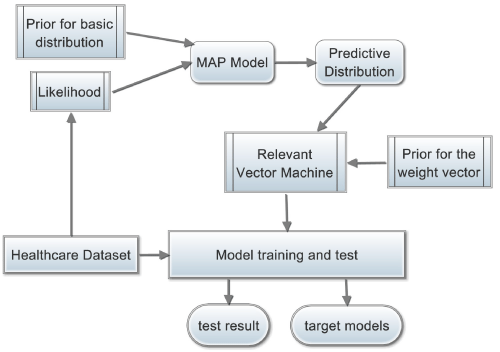
where y∈R is a target variable and d x∈R^dis a d- dimension feature vector. Φ is a set of basic functions, where $Φ_{i} (x) : R^{d} \to R$ ∈ is Gaussian noise with zero mean and unknown variance. In this work, we limit Φ to be a set of random initialized Gaussian distributions. The goal is to derive the posterior distribution p(w|D) given training dataset D and the predictive distribution p(y|x,D) given training dataset D and a test example x. Moreover, to cut down the computational cost of both training and test, a sparse combination is preferred, meaning that in the weight vector w, there are a lot of elements are zero. We will show that the problem of finding a sparse weight vector can be solved by a Relevant Vector Machine (RVM), which is a Sparse Bayesian Learning (SBL) model [17,18]. Figure 1 sketches the main idea of this article.

Figure 1: The main idea of sparse Bayesian learning..



Figure 1:  The main idea of sparse Bayesian learning.

The remainder of this article is organized as following. In Section 2 we formally give the sparse Bayesian model. In Section 3 we present the evaluation results of the propsed model compared with some recent methods. And finally we conclude the article in Section 4.

The Sparse Bayesian Model

We aim at building a model to capture the predictive distribution of the prediction target. Let $Φ = {φ_{1}, φ_{2}, ..., φ_{m}}$ be a set of known basic distributions. Given a training dataset $D = {(x_{i}, y_{i}), i = 1, ..., N}$ , the likelihood can be expressed as p(y|x,w). And if we introduce a proper prior, we can get the Maximum a Prior (MAP) distribution. Thus the optimal w* can be expressed as:

w^{*} = \arg \max_{w} p (y / w, x) p (w) = Φ^{T} {(λ I + Φ Φ^{T})}^{- 1} y (2)

where λ is a square ratio between the variance of ε and w. p(y|w,x) is the likelihood function and p(w) is the prior for the weights w. It is well known that in SBL an ARD prior is often imposed on w by introducing a set of parameter α [19]. Thus we have:

p (w / α) = \prod_{i = 0}^{N} N (w_{i} / 0, α_{i}^{- 1}) (3)

where a is the precison controlling each element of w. If is infinity, the corresponding would be driven to zero.

The likelihood p(y|x,w) can be written as following:

p (y / x, w) = \prod_{i = 0}^{N} p (y_{i} / x_{i}, w)

where $p (y_{i} / x_{i}, w)$ is the probability of each sample. Since the distribution is controlled by two parameters, we can use point estimation method to evaluate them.

According to Bayesian formula, we can derive the posterior distribution with likelihood, prior and the evidence as following:

p (w | D, α, ε) = N (w | m, Σ) (5)

where $m = ε Σ Φ^{T} y$ and $Σ = {(d i a g (α_{i}) + ε Φ^{T} Φ)}^{- 1}$ . Note that Φ can be a kernel matrix if we make use of a Gaussian process prior. In our work, we use a radius basic function kernel over D to generate such prior, such that ${(Φ)}_{i j} = k_{R B F} (x_{i}, x_{j})$ where $k_{R B F} = \exp (- d {(x_{i}, x_{j})}^{2})$ . The optmial α and ε can be determined by solving a type-2 maximum likelihood problem, where we have: $p (y / x, α, ε) = \int p (y / x, w, ε) p (w / α) d w (6)$

According the formula of the convolution of two normal distribution, the above marginal likelihood can be solved analytically in its logarithm form as following:

[Sorry. Ignored \begin{aligned} … \end{aligned}] (7)

Where $C = ε^{- 1} I + Φ d i a g {(α_{i})}^{- 1} Φ^{T}$ . The optimal a and e can be obtained through a iteration procedure, where we have:

$α_{i}^{*} = \frac{γ_{i}}{m^{2}_{i}} (8)$

${(ε^{*})}^{- 1} = \frac{∥ y - Φ m ∥^{2}}{N - Σ_{i} γ_{i}} (9)$

$γ_{i} = 1 - α_{i} Σ_{i i} (10)$

An important thing should be noticed is that during the iteration procedure, a large number of α_i would be driven to infinity, leading to only a small amount of non-zero w_i . Hence we obtain a sparse model. The model sparsity is originated from the fitness between basic distributions and the groundtruth distribution implied in the training dataset D. If a basic distribution does not go along with some direction of the groundtruth, it will be gradually driven out by increasing the corresponding α.

After we find the optimal α and ε, we can derive the predictive distribution given a test sample x_η. The predictive distribution is the marginal of w. It is the integration on w with the convolution of posterior and prior. We have:

[Sorry. Ignored \begin{aligned} ... \end{aligned}] (11)

Where $δ^{2} (x_{η}) = {(ε^{*})}^{- 1} + φ {(x_{η})}^{T} Σ (x_{η})$ . Hence we can get a predictive distribution of a given test example x_η. However, there is still one thing to be addressed. The proposed model is naturally based on a regression setting, meaning that the target variable y∈R. In healthcare data analysis, the target variables are discreate in many cases. To make the proposed method suitable for classification, we introduce a sigmoid function into our model. A sigmoid function can typically be expressed as $f (x) = \frac{1}{1 + e^{- x^{,}}}$ , whose range is (0,1]. Each input can be compressed to a standard range. We use sigmoid function to convert the output of our model to (0,1] and then use a discriminate function to get a class label.

Evaluation and Results

Dataset description

We evaluate the proposed method on two healthcare datasets from KDDCup, a famous data mining competition. The first is a Pulmonary Embolism (PE) diagnosis dataset, and the seccond is a Breast Cancer clinical data set. We briefly denote these two datasetsas M1 and M2. For M1, the target is to classify whether an individual has PE given an image. A total of 4429 candidates were identified in the candidate generation procedure: 3038 candidates appear in thetraining set, and 1391 appear in the test set. Each candidate is a cluster f voxels (the 3-D analog of pixels) with gray values for each voxel in the cluster. Each candidate was then l abeled as a PE or not based n proximity to a 3-D landmark provided by an expert. The image is expressed as a 69-ary feature vector. The detail of M1 is listed in Table 1. For M2, the analysis target is to identify whether a patient has breast cancer. A breast cancer screen typically consists of 4 X-ray images; 2 images of each breast from different directions (MLO and CC). Each image is represented by several candidates . For each candidate, there are image ID and the patient ID, (x,y) location, several features, and a class label indicating whether or not it is malignant. For convenience,the dataset has been preprocessed and each sample has a vector-form. Table 2 lists the detail of M2. And three examples of raw clinical data have been presented in Table 3. The first one and the second one set are from train data, and the third one is from the test data. Notethat the first two columns supply the patient identifier and the PE identifier. The PE indentifier is also our target lable variable. If it is a PE, the lable is a positive number, if it is not a PE, the label is set to 0.In the test data, all labels are set to -1, which means unknown.

Table 1: Description of M1.



  
    No. 
    Name 
    Type 
    Description 
  
  
    1
    Patient ID
    Number
    4 bits
  
  
    2
    Label
    Boolean
    whether or not there is PE
  
  
    3
    Size feature
    Real
    image size
  
  
    4
    spatial shape feature
    Real
    3-ary vector
  
  
    5
    Location feature
    Real
    2-ary vector
  
  
    6
    neighborhood intensity feature
    Real
    2-ary vector
  
  
    7
    simple intensity statistic
    Real
    4-ary vector
  
  
    8
    neighborhood feature
    Real
    4-ary vector
  
  
    9
    neighborhood intensity feature
    Real
    18-ary vector
  
  
    10
    shape feature
    Real
    26-ary vector
  
  
    11
    anatonical feature
    Real
    4-ary vector
  
  
    12
    neighborhood feature threshold
    Real
    2-ary vector
  
  
    13
    intensity contrast feature
    Real
    5-ary vector
  
  
    14
    Shape neighbor feature
    Real
    34-ary vector



Table 1:  Description of M1.

Table 2: Description of M2.



  
    No. 
    Name 
    Type 
    Description 
  
  
    1
    Ground truth label
    Boolean
    +1/-1
  
  
    2
    Image-Finding-ID
    Number
    a unique non-negative identifier
  
  
    3
    Study-Finding-ID
    Number
    identify a lesion
  
  
    4
    LeftBreast
    Boolean
    if the candidate was generated from the left breast
  
  
    5
    MLO
    Boolean
    from an MLO image or not
  
  
    6
    X-location
    Number
    X-pixel location
  
  
    7
    Y-location
    Number
    Y-pixel location
  
  
    8
    X-nipple-location
    Number
    X-pixel nipple location
  
  
    9
    Y-nipple-location
    Number
    Y-pixel nipple location



Table 2:  Description of M2.

Table 3: Examples of raw clinical data in M1.



  
    Feature examples 
    F1 
    F2 
    F3 
    F4 
    ? 
    F115 
  
  
    No.1
    3000
    0
    336
    284
    ? 
    0.024697524
  
  
    No.2
    3000
    1
    328
    287
    ? 
    0.006415986
  
  
    No.3
    3002
    -1
    250
    275
    ? 
    -0.31899535



Table 3:  Examples of raw clinical data in M1.

Evaluation

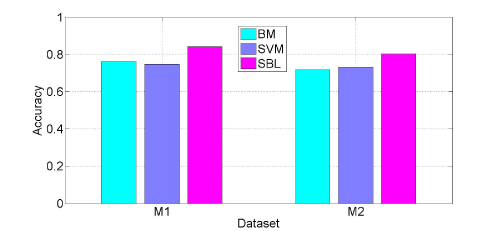
We perform two kinds of evaluation to illustrate the effectiveness of the proposed method. The first is to evaluate the performance of the proposed model compared with the traditional Bayesian Model(BM) and Support Vector Machine (SVM) classifier. The second is to illustrate how sparse our model is, and the relationship between the model sparsity and the performance. For both cases, we use the same setting as following. The whole dataset is randomly divided into training set and test set with ratio 3:7. We only consider two classes classification problem. Since the two datasets are multiple classes, we convert them into m sub problems, each problem is a one-versus-restclassification problem. For the compared Bayesian model, a flat prior is used in the model. For SVM, the default parameter is set and radius basic function is used as kernel function. In both cases the distancefunction between samples is Euclidean distance function. Zeroone loss is used as the loss function for accuracy evaluation. Figure 2 shows the compared results for the first case. From Figure 2, we can see that compared with the traditional Bayesian model and SVM classifier, our SBL model has the best performance in both datasets. It leads to 83% and 80% accuracy respectively.