A New Quantitative Inversion Method for Reservoir Interwell Dynamic Connectivity at Extra High Water Cut Stage

Editorial

The reservoir interwell water flooding status and oil-water movement direction at extra high water cut stage are complex, and inefficient and ineffective circling are becoming increasingly serious. The strengthening inference of reservoir interwell dynamic connectivity has been an important part of reservoir evaluation and dynamic analysis. According to the system analysis method, a weighted grey correlation model based on optimized entropy is proposed, and the inversion decision model for characterizing interwell dynamic connectivity of injection-production system is established, and reservoir interwell dynamic connectivity is inversed quantitatively with injection-production dynamic data. The interwell dynamic connectivity in the G20-39 district of Daqing LaSaXing oil field is inversed by using the established model; the interwell dynamic connectivity map is drawn. By adjusting the measure schemes for oil and water wells, a better development effect can be obtained, which verifies the validity of the presented method. The practice shows that this method has strong adaptability and accurate inversion result, the interwell dynamic connectivity inversed by this method is accord with the actual situation of reservoir, and can provide the foundation for the implementation of development adjustment measure of LaSaXing oilfield at extra high water cut stage.

Keywords: Grey system; Grey correlation degree; Grey entropy; Interwell dynamic connectivity; Reservoir dynamic; Inversion

Introduction

Strengthening the estimation of d reservoir interwell dynamic connectivity and identifying the Injected water flow direction have been an important part of reservoir evaluation and dynamic analysis at extra high water cut stage, and it is important significance for implementing the scheme and enhancing oil recovery [1-2]. At present, the frequently-used methods of reservoir interwell dynamic connectivity mainly include geochemical method, tracer test, well testing, numerical simulation, and soon [3-8]. The implementations of these methods are more complex, expensive, and can affect the normal production of oilfield. In recent years, it has been mainly popular that the interwell dynamic connectivity is inversed through using production data analyzed by statistical methods at home and abroad, which has been an important method for research the reservoir connectivity, the method models mainly include correlation analysis model [9-10], multiple linear regression model [11], capacitance model [12-14], system analysis model [15-16], and soon. The correlation analysis method is one of the reservoir engineering methods for reservoir dynamic analysis. The grey correlation analysis in grey theory is the most widely used and applied to the reservoir dynamic analysis because of its simple calculation, clear mechanism, advantages of clear required less data and strong adaptability. Wang [17] and Liu [18] separately calculated the correlation of interwell dynamic data by using the rate correlation degree and gray correlation analysis method, then the strong or weak dynamic connectivity between oil and water well is quantitatively determined through the correlation value. But both the rate correlation degree and the grey correlation analysis method take the simple arithmetic average value of the grey correlation coefficient at each time point as the grey correlation degree, which may cause the loss of information and local point correlation value controls the whole grey correlation trend. Multiple linear regression model, capacitance model and system analysis model have disadvantages of complex calculation, difficult application to the inversion for interwell dynamic connectivity, and they cannot inverse the interwell connectivity between production wells without considering interwell fluid interference between production wells. Aiming at above problems, this paper views the reservoir as a complicated nonlinear grey system, grey correlation coefficient is unequally weighted average to calculate grey correlation degree through combining with the grey sequence entropy analysis method, the weighted grey correlation model based on optimized entropy is established, and the inversion decision model for characterizing interwell dynamic connectivity of injection-production system is established, and reservoir interwell dynamic connectivity is inversed quantitatively with injection-production dynamic data.

Interwell Dynamic Connectivity Model

The principle

Reservoir is a complicated nonlinear dynamic balance system, according to the systematology idea, injection well, production well and interwell pore throat passage of reservoir are viewed as a whole grey system. Practice has proved that the production well performance of reservoir at extra high water cut stage is mainly affected by water flooding situation of corresponding injection well and the fluid disturbance around the production well. After water is injected into the reservoir, the crude oil and part of the inefficient, ineffective water are displaced to oil well through the good connectivity reservoir, during displacement, the change of water injection can make dynamic index of corresponding production well fluctuate, or the enhanced liquid, controlled liquid measures of a production may make dynamic index of around production well fluctuate, which is a feature reflection of reservoir connectivity between wells. The interwell grey correlation degree reflects the strength of the interaction between wells. The interwell connectivity and oil-water movement direction can be determined through calculating the grey correlation degree between the input signal (water injection) of injection well and the output signal of corresponding production well (liquid production, oil production, water cut, bottom hole flowing pressure) in a certain period of time, or through calculating the correlation degree between the mass production of a production well and the output signal of the surrounding production well. Therefore, injection-production dynamic data are used to inverse the reservoir interwell dynamic connectivity, which not only can obtain the more accurate and effective result, also is a relatively simpler and cheaper method. If the grey correlation between the water injection of a injection well and the dynamic index of a surrounding production well is high, it shows that the water flooding degree of the injection well to the production well is strong, the reservoir interwell connectivity is good, the water flow direction mainly points to the production well which is mainly affected by the injection well. If the grey correlation degree between the liquid production of a production well and the output signal of a surrounding production well is high, it shows that the connectivity between the production well is good, the interwell interference degree is strong, water flow direction occurs steering, the surrounding production well is mainly controlled by the production well, clarifying these problems can formulate the feasible development adjustment measures, that is the directions between injection and production wells in which is the increasing water injection is to increase oil production, which is the increasing injection is to increase water production (It indicates that the preponderant flow channel has formed ), which is the increasing of oil production and water production, and the directions between production wells in which should be to enhance liquid, and which should be to control liquid, thus it provides reliable basis for adjusting the injection-production relationship and liquid production structure and changing the liquid flow direction.

Establishment of inversion model

According to the above principle, Supposing there are n injection wells w₁,w₂…, w_n and m production wells O₁,O₂,…,O_m around a production well in system, eight correlations are established between the oil production, liquid production, water cut, Bottom Hole Flowing Pressure (BHP) of a production well and the water injection of corresponding injection well and the liquid production of surrounding production well, which are water-oil, waterliquid, water-water cut, water-BHP, liquid-oil, liquid-liquid, liquidwatercut, liquid-BHP, theirs correlation degrees are respectively calculated to construct an attribute matrix E:

$E=\begin{array}{c}\begin{array}{cccc}oil& liq& f_w& p_{wf}\end{array}\\ \begin{array}{c}{\text{w}}_1\\ ⋮\\ w_n\\ o_1\\ ⋮\\ o_m\end{array}\left(\begin{array}{cccc}{\gamma }_{11}& {\gamma }_{12}& {\gamma }_{13}& {\gamma }_{14}\\ ⋮& ⋮& ⋮& ⋮\\ {\gamma }_{n1}& {\gamma }_{n2}& {\gamma }_{n3}& {\gamma }_{n4}\\ {\gamma }_{n\text{+}11}& {\gamma }_{n\text{+}12}& {\gamma }_{n\text{+}13}& {\gamma }_{n\text{+}14}\\ ⋮& ⋮& ⋮& ⋮\\ {\gamma }_{n\text{+}m1}& {\gamma }_{n\text{+}m2}& {\gamma }_{n\text{+}m3}& {\gamma }_{n\text{+}m4}\end{array}\right)\end{array}\text{ (1)}$

A comprehensive correlation matrix is calculated and obtained through comprehensively combining with the weight matrix Q of oil production, liquid production, water cut and BHP, that is the inversion model of the interwell dynamic connectivity coefficient T between the surrounding production well, injection well and center production well:

$T=E\otimes Q^T=\begin{array}{c}{w}_1\\ ⋮\\ w_n\\ o_1\\ ⋮\\ o_m\end{array}\left(\begin{array}{c}{T}_1\\ ⋮\\ T_n\\ T_{n\text{+}1}\\ ⋮\\ T_{n\text{+}m}\end{array}\right)\text{ (2)}$

In the formula, the weight matrix Q = (0.3419, 0.2503, 0.3253, 0.0826).

The correlation degree γ in the matrix E is solved by using the weighted grey correlation model based on the grey entropy optimization. Supposing the oil production or liquid production, water injection and so on as the system time sequence:

Where, X₀ is the main behavior sequence, X_i is the comparison sequence in system. For ρ^€(0,1), there is

$\gamma (x_0(k),x_i(k))=\frac{\underset{i}{\min }\underset{k}{\min }\left|x_0(k)-x_i(k)\right|+\rho \underset{i}{\max }\underset{k}{\max }\left|x_0(k)-x_i(k)\right|}{\left|x_0(k)-x_i(k)\right|+\rho \underset{i}{\max }\underset{k}{\max }\left|x_0(k)-x_i(k)\right|}\text{ (4)}$

$\gamma (X_0,X_i)={\displaystyle \sum _{k=1}^n{\omega }_k\gamma (x_0(k),x_i(k))}\text{ (5)}$

γ(x₀(k),x_i(k)) is called as grey correlation coefficient, γ(X₀,X_i) is the weighted grey correlation degree between X₀ and X_i. Where, ρ is the resolution coefficient is equal to 0.5; ω_k is the weight of point?, ${\displaystyle \sum _{k=1}^n{\omega }_k=1(0<{\omega }_k<1)}$ω_kIn order to solve the model parameter ?k, the grey entropy analysis method is used to determine the weight of correlation coefficient [19].

is the model parameter to be determined.

2 Solution of model parameters

In order to solve the model parameter ω_k, the grey entropy analysis method is used to determine the weight of correlation coefficient [19].

The specific process is as follows.

Map : R_j → P_j

Definition 1, calling the mapping:

$p_k=\frac{{\omega }_k\gamma (x_0(k),x_i(k))}{{\displaystyle \sum _{k=1}^n{\omega }_k\gamma (x_0(k),x_i(k))}}\text{ (6)}$

Above formula is the distribution mapping of the weighted grey correlation coefficient, the mapping ?_? is the distribution density of the weighted grey correlation coefficient, and meets the ${\displaystyle \sum _{k=1}^n{p}_k=1}$

Definition 2, calling function:

$H_{\otimes }(R_i)=-{\displaystyle \sum _{k=1}^n{p}_k\ln p_k}\text{ (7)}$

Above formula is the weighted grey correlation entropy of X_i, any drives ?_? to equally change will make the correlation entropy H_⊗ (R_i) increase.

Considering the influence of the comparison sequence on the main behavior sequence should be remain stable, that is the weighted correlation coefficient should maintain balanced, ?_? should maintain balanced, so there is:

$\begin{array}{l}\max H_{\otimes }(R_i)=-{\displaystyle \sum _{k=1}^n{p}_k\ln p_k}\text{ (8)}\\ s.t.p_k\ge 0\\ s.t.{\displaystyle \sum _{k=1}^n{p}_k=1}\end{array}$

For the extremum problem of above function, the weight vector is obtained through constructing the Lagrange function and operating matrix under the constraint condition of grey correlation entropy maximization:

Ω = Г_-1 b (9)

where,

$\Gamma =\left[\begin{array}{ccccc}{\gamma }_1& -{\gamma }_2& & & \\ & \gamma {}_2& -{\gamma }_3& & \\ & & \ddots & & \\ & & & {\gamma }_{n-1}& {\gamma }_n\\ 1& 1& 1& 1& 1\end{array}\right]$$\Omega =\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ ⋮\\ {\omega }_{n-1}\\ {\omega }_n\end{array}\right]$$b=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]\text{ (10)}$

The model with higher resolution can well control the influence of fluctuation of the partial correlation coefficient on overall correlation. In view of the advantages of the model can accurately calculate the weight ω_k, and then inverse the reservoir interwell dynamic connectivity.

Example Analysis

The G20-39 block in Daqing LaSaXing oilfield was selected to apply the above model. This block mainly develops PI reservoir group, and there are 13 sedimentary units. The main reservoir sand body distribution is striped and sheet like, and non-essential reservoir sand body distribution is narrow stripe, scattered and poorly developed. The block was put into operation in 1983, it applied the four-spot water flooding pattern, and well spacing was 350 meters. Since 1999 the block has entered into extra high water cut stage, the production decreasing magnitude is large, the water cut is rising rapidly, it is urgent need to adjust the current water injection scheme, and select the applicable measure for injection well and production well, thus, it is very important to carry out the interwell dynamic connectivity research. The interwell dynamic connectivity in the block was inversed according to its computation steps.

Understanding of interwell dynamic connectivity

The first thing is to understand the interwell connectivity relationship, the connectivity degree can be determined through the correlation degree value between injection well and production well in the each injection-production system. According to the evaluation standard definition of reservoir dynamic grey correlation degree in LaSaXing oilfield, if the correlation degree T is greater than or equal to 0.8, the connectivity is good; if the correlation degree T is between 0.6 and 0.8, the connectivity is little good; if the correlation degree T is less than or equal to 0.6, the connectivity is poor. The model was used to analyze the interwell correlation degree respectively between the monthly water injection of injection well and monthly oil production, monthly liquid production, monthly water cut, BHP of surrounding production well, respectively between the monthly liquid production and monthly oil production, monthly liquid production, monthly water cut, bottom hole flowing pressure of surrounding production well during 2013 in the G20-39 block, by which could determine the connectivity between injection well and production well, and between production well. Seen from the (Table 1) and (Figure 1), the results show that the connectivity degree between injection well and the surrounding production well are not uniform. The correlation degree analysis results are in good agreement with the actual connectivity, which prove that the inversion analysis is effective and accurate. Seen from the results, the interwell connectivities in the G20-39 block belong to the little good class.

Table 1: Correlation degree analysis result of injection-production well system in G20-39 block.

  

    
Injection well
    
Production
      
well
    
water-oil
    
water-liquid
    
water-water cut
    
water-BHP
    
correlation degree T
  
  

    
G20-41
    
G20-39
    
0.749
    
0.827
    
0.878
    
0.756
    
0.811
  
  

    
G22-48
    
0.791
    
0.802
    
0.845
    
0.728
    
0.806
  
  

    
G22-41
    
0.79
    
0.782
    
0.754
    
0.685
    
0.768
  
  

    
G18-41
    
0.763
    
0.75
    
0.744
    
0.694
    
0.748
  
  

    
G16-39
    
G103
    
0.759
    
0.818
    
0.869
    
0.735
    
0.808
  
  

    
G18-41
    
0.699
    
0.743
    
0.744
    
0.697
    
0.725
  
  

    
G24-43
    
G22-41
    
0.733
    
0.751
    
0.752
    
0.714
    
0.742
  
  

    
G26-45
    
0.772
    
0.821
    
0.854
    
0.732
    
0.808
  
  

    
G22-48
    
0.602
    
0.667
    
0.676
    
0.641
    
0.646
  
  

    
G24-41
    
0.718
    
0.744
    
0.746
    
0.685
    
0.731
  
  

    
G26-41
    
G26-43
    
0.648
    
0.592
    
0.582
    
0.528
    
0.603
  
  

    
G28-41
    
0.683
    
0.711
    
0.716
    
0.669
    
0.700
  
  

    
G24-41
    
0.649
    
0.731
    
0.747
    
0.675
    
0.704
  
  

    
G18-37
    
G20-39
    
0.592
    
0.629
    
0.631
    
0.557
    
0.611
  
  

    
G103
    
0.716
    
0.726
    
0.727
    
0.674
    
0.719
  
  

    
G18-35
    
0.738
    
0.751
    
0.713
    
0.701
    
0.730
  

Table 1:  Correlation degree analysis result of injection-production well system in G20-39 block.

Close

Figure 1: The connectivity map between injection well and production well in G20-39 block.

    

    

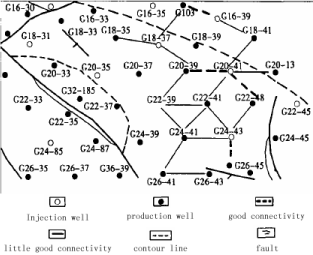
    Figure 1:  The connectivity map between injection well and production well
in G20-39 block.
    
    

Close

Adjustment measure and effect analysis

According to the correlation degree between injection well and the production well around the first line, the interwell connectivity and the water direction of well were determined, the large correlation degree was the main water direction, and the small correlation degree was the secondary water direction. On this basis, the corresponding profile control, water plugging, fracturing and other adjustment measures were taken.

According to the correlation degree results, the water injection schemes of water wells in the G20-39 block were adjusted. Seen from (Table 2), the water injection schemes of 5 well times and 4 layers were adjusted, the daily injection allocation was reduced from 180 m³/d to 160 m³/d, and the daily real injection was reduced from 180 m³/d to 163 m³/d. Among them, the real reduction water of 3 well times and 3 layers was 59 m³, the actual enhance water of 2 well times was 42 m³.

Table 2: Adjustment table of water injection scheme.

  

    
Item
    
Wellname
    
Adjustment time
    
Adjustment layer
    
Daily injection allocation
    
Daily real injection
  
  

    
Old scheme /m3
    
New scheme /m3
    
Difference/m3
    
Old scheme /m3
    
New scheme /m3
    
Difference /m3
  
  

    
Reduced water
    
G20-41
    
2013-06
    
PI3-4
    
50
    
20
    
-30
    
48
    
23
    
-25
  
  

    
G16-39
    
2013-09
    
PI4
    
40
    
20
    
-20
    
36
    
22
    
-14
  
  

    
G24-43
    
2013-05
    
PI6 and below
    
40
    
20
    
-20
    
44
    
24
    
-20
  
  

    
Subtotal
    
130
    
60
    
-70
    
128
    
69
    
-59
  
  

    
Enhanced water
    
G26-41
    
2013-09
    
Whole well
    
50
    
70
    
20
    
52
    
65
    
13
  
  

    
G18-37
    
2013-07
    
PI5
    
Stop
    
30
    
30
    
0
    
29
    
29
  
  

    
Subtotal
    
50
    
100
    
50
    
52
    
94
    
42
  
  

    
Total
    
180
    
160
    
-20
    
180
    
163
    
-17
  

Table 2:  Adjustment table of water injection scheme.

Close

Through implementing the adjustment scheme, the surrounding connected wells achieved a good development effect. Seen from the statistical results of 6 connected wells without measures in (Table 3), the decreasing magnitude had slowed down, and the rising rate of water cut had been effectively controlled.

Table 3: Dynamic change of connected wells without measures.

  

    
Date
    
Daily liquid production
      
/t
    
Daily oil production
      
/t
    
Decreasing magnitude /%
    
Daily water production /m3
    
Water cut/%
    
Water cut rising/%
    
BHP/MPa
  
  

    
2011-12
    
206
    
16.0
    
/
    
190.0
    
92.2
    
/
    
3.38
  
  

    
2012-12
    
196
    
11.4
    
28.8
    
184.6
    
94.2
    
2.0
    
3.71
  
  

    
2013-12
    
176
    
9.9
    
13.2
    
166.1
    
94.4
    
0.2
    
3.79
  

Table 3:  Dynamic change of connected wells without measures.

Close

In addition, according to the understanding of interwell connectivity, the water plugging measures of 2 production wells in the G20-39 block were taken. Seen from the results in (Tables 4 & 5), Fluid production were controlled obviously, oil production increased, and water cut and BHP decreased significantly, achieved a good development effect. These adjustment measures effect further verified the correctness of the interwell dynamic connectivity inversion method.

Table 4: Adjustment scheme of production well.

  

    
Production
      
well
    
Connected injection
      
well
    
Correlation coefficient
    
Date
    
Layer
    
Measure
  
  

    
Water-liquid
    
Water-oil
    
Water-water cut
    
Water-BHP
  
  

    
G20-39
    
G20-41
    
0.797
    
0.745
    
0.849
    
0.736
    
2014-02
    
PI6-7
    
water plugging
  
  

    
G26-44
    
G24-43
    
0.801
    
0.758
    
0.863
    
0.741
    
2014-02
    
PI7
    
water plugging
  

Table 4:  Adjustment scheme of production well.

Close

Table 5: Contrast effect of before and after measures of production well.

  

    
Production
      
well
    
Before water plugging (2013-12)
    
After water plugging (2014-03)
  
  

    
Daily liquid
      
production
      
/t
    
Daily oil
      
production
      
/t
    
Water cut
      
/%
    
BHP
      
/MPa
    
Daily liquid
      
production
      
/t
    
Daily oil
      
production
      
/t
    
Water cut
      
/%
    
BHP
      
/MPa
  
  

    
G20-39
    
61
    
3
    
94.8
    
6.01
    
31
    
4
    
86
    
3.12
  
  

    
G26-44
    
65
    
3
    
95.3
    
8.38
    
29
    
3
    
90.2
    
2.95
  
  

    
Total
    
126
    
6
    
95.2
    
7.20
    
60
    
7
    
88.3
    
3.04
  

Table 5:  Contrast effect of before and after measures of production well.

Close

Conclusion

(1) The inversion model of reservoir interwell dynamic connectivity is established based on the system analysis method, and gives the solution method of the model parameters, physical meaning of the model is clear, can effectively characterize the reservoir interwell dynamic connectivity.

(2) The inversion results of interwell dynamic connectivity in the G20-39 block show that the connectivity degree between injection well and the surrounding production well are not uniform, and the correlation degree analysis results are in good agreement with the actual connectivity.

(3) According to the inversion results of interwell dynamic connectivity, the corresponding profile control, water plugging, fracturing and other adjustment measures of injection and production well in the G20-39 block were taken, achieved a good development effect, which shows that the inversion result of interwell dynamic connectivity is consistent with the actual situation of the reservoir by the established method, this method can quantitatively characterize the reservoir interwell dynamic connectivity, and provide the foundation for LaSaXing oilfield to implement the adjustment measures at extra high water cut stage.

References

1. Hird KB, Dubrule O. Quantification of reservoir connectivity for reservoir description applications [R]. SPE 30571. 1995.
2. Yousef AA, Jensen JL, Lake LW. Integrated Interpretation of Interwell Connectivity Using Injection and Production Fluctuations [J]. Mathematical Geosciences. 2009; 41: 81-102.
3. Wen ZG, Zhu D, Li YQ. Oil layer connectivity in the sixth block of Gudong Oilfield, the evidence from gas chromatography fingerprint technique [J]. Petroleum Exploration and Development. 2004; 31: 82-83.
4. Zhang Z, Chen MQ, Gao YL. Estimation of the connectivity between oil wells and water injection wells in low-permeability reservoir using tracer detection techniques [J]. Journal of Xi' a Shiyou University: Natural Science Edition. 2006; 21: 48-49.
5. Liao HW, Wang C, Zuo DR. Applying transient testing to the judgment of inter-well connectivity[J]. Petroleum Exploration and Development. 2002; 29: 87-89.
6. Yang J, Chen Q,Li JL, Liu ZC. Interwell-connectivity analysis for fracture-vug reservoirs in the block-4 of Tahe oilfield, Tarim Basin [J]. Oil & gas geology. 2012; 33: 484-489.
7. Guo Kl, Zou L. Analyzing Inter-well Connectivity of Low-permeability Reservoirs with Pulse-testing Method [J]. Journal of Yangtze University (Natural Science Edition). 2007; 4: 39-41.
8. Demiryurek U, Banaei-Kashanin F, Shahabi C, Wilkinson FG. Neural-Network based Sensitivity Analysis for Injector-Producer Relationship Identification [C]. SPE 112124. 2008.
9. Heffer K, KJ, Fox, RJ, McGill, CA. Novel Techniques Show Links between Reservoir Flow Directionality, Earth Stress, Fault Structure and Geo mechanical Changes in Mature Water floods [J]. SPEJ. 1997; 2: 91-98.
10. Refunjol BT, Lake LW. Reservoir characterization based on tracer response and rank analysis of production and injection rates in reservoir characterization-recent advances [J]. AAPG Bulletin. 1999; 18: 198-201.
11. Albertoni A, Lake LW. Inferring Interwell Connectivity Only from Well-Rate Fluctuations in Waterfloods [J]. SPE-83381-PA. 2003: 6-16.
12. Dinh A, Tiab D. Inferring Interwell Connectivity from Well Bottom hole-Pressure Fluctuations in Waterfloods [J]. SPEREE. 2008; 874-881.
13. Sayarpour M, Kabir CS, Lake LW. Field Applications of Capacitance-Resistive Models in Waterfloods [C]. SPE-114983-PA. 2008.
14. Yousef AA, Gentil PH, Jensen JL, Lake L. A Capacitance Model to Infer Interwell Connectivity from Production and Injection Rate Fluctuations. SPEREE. 2006; 630-646.
15. Feilong L, Jerry M, Nejad A. Forecasting injector-producer relationships from production and injection rates using an extend kalman filter [R]. SPE 110520. 2009; 4: 653-664.
16. Zhai D, Mendel M, Liu FA. New method for Continual Forecasting of Interwell Connectivity in Waterfloods Using an Extended Kalman Filter [C]. SPE 121393. 2009.
17. Wang ZG, Zhang JC, Song KP, Huang XL, Zhang XH. Analyze interwell communication by rate correlation [J]. Special oil and gas reservoirs. 2011; 18: 91-93.
18. LIU Shi J,Peng XD, LI J. A Method of Inverting the Dynamic Connectivity between the Injection and Production Wells Based on Production Data [J]. Science Technology and Engineering. 2013; 13: 145-148.
19. Wang ZX, Dang YG, Cao MX. Weighted degree of grey incidence based on optimized entropy [J]. Systems Engineering and Electronics. 2010; 32: 774-776.

Download PDF

Citation: Wen H, Sun N, Liu Y, Lu J and Li B. A New Quantitative Inversion Method for Reservoir Interwell Dynamic Connectivity at Extra High Water Cut Stage. Austin J Hydrol. 2015; 2(1): 1015. ISSN : 2380-0763

Home

Journal Scope

Online First

Current Issue

Editorial Board

Instruction for Authors

Submit Your Article

Contact Us