Research Article
Austin J Nanomed Nanotechnol.2014;2(2): 1013.
Cluster model expanded to C-nanostructures: Fullerenes, tubes, graphenes and their buds
Francisco Torrens, Gloria Castellano
1Institute for Molecular Science, University of Valencia, Spain
2Faculty of Veterinary and Experimental Sciences, Valencia Catholic University, Spain
*Corresponding author: : Francisco Torrens, Institute for Molecular Science, University of Valencia, Building Institutes Paterna, P. O. Box 22085, E-46071 Valencia, Spain
Received: January 02, 2014; Accepted: January 23, 2014; Published: January 30, 2014
Abstract
The existence of nanographene (GR) and GR-fullerene bud (GR-BUD) in cluster form is discussed in organic solvents. Theories are developed based on columnlet, bundlet and droplet models describing size-distribution functions. The phenomena present a unified explanation in columnlet model, in which free energy of GR involved in cluster comes from its volume, proportional to number of molecules n in cluster. Columnlet model enables describing distribution function of GR stacks by size. From purely geometrical considerations, columnlet (GR/GR-BUD), bundlet [single-wall carbon nanotube (SWNT) (CNT) (NT) and NT-fullerene bud (NT-BUD)] and droplet (fullerene) models predict dissimilar behaviours. Interaction-energy parameters of GR/GR-BUD are taken from C60. An NT-BUD behaviour or further is expected. Solubility decays with temperature result smaller for GR/GR-BUD than SWNT/NT-BUD than C60, in agreement with lesser numbers of units in clusters. Discrepancy between experimental data of the heat of solution of fullerenes, CNT/NT-BUDs and GR/GR-BUDs is ascribed to sharp concentration dependence of the heat of solution. Diffusion coefficient drops with temperature result greater for GR/GR-BUD than SWNT/NT-BUD than C60, corresponding to lesser number of units in clusters. Aggregates (C60)13, SWNT/NT-BUD7 and GR/GR-BUD3 are representative of droplet, bundlet and columnlet models.
Keywords: Solubility of graphene-fullerene bud; Columnlet cluster model; Bundlet cluster model; Droplet cluster model; Nanobud; Fullerene
Introduction
Nanoparticles interest arose from shape-dependent physical properties of nanoscale materials [1,2]. Single-wall C-nanocones (SWNCs) (CNCs) allowed curved-structures nucleation/growth suggesting pentagon role that, introduced into nanographene (GR) via extraction of a 60° sector, forms a cone leaf. Pentagons in SWNC apex are analogues of single-wall C-nanotube (SWNT) (CNT) tip topology. Classes of positive-curvature CNCs [3-5] /Clar theory [6-10] were analyzed. Ends of SWNTs predicted electronic states related to GR topological defects [11]. Resonant peaks in density of states appeared in SWNTs [12] /multiple-wall CNTs (MWNTs) [13]. SWNCs with discrete opening angles θ = 19°, 39°, 60°, 85° and 113° in pyrolytic C were explained by cone wall model of wrapped GR sheets, where geometrical requirement for seamless connection accounted for semi-discrete character [14]. Total disclinations are multiples of 60° for P≥0 pentagons in SWNC apices. From symmetry/Euler theorem five SWNC types are obtained from continuous GR sheet for P = 1-5: sin(θ/2) = 1 - P/6, leading to flat discs and caped SWNTs matching to P = 0 and 6, respectively; most abundant SWNC (P = 5) is nanohorn (SWNH). Configurations exist for given cone angle depending on pentagon arrangement: isolated pentagon rule led to somers more stable than grouped ones [15]; others derived from ab initio calculations [16]. Functionalization of SWNCs with NH4+ improved solubility [17] that was achieved by skeleton [18-20]/cone-end [21] functionalization and supramolecular p-p stackings [22-24] with pyrenes/porphyrins. An MNDO computation of BN substitutions in C60 showed analogous B30N30[25]. Substitution in Cdiamond by alternating B/N provided BN-cubic [26]. BN-hexagonal (h) resembles Cgraphite since fused planar six-membered B3N3 rings; however, interlayer B-N exist. BN nanotubes were visualized [27-29]. BN-h was proposed [30]. BN nanocones were observed [31-33] /calculated [34-39]; most abundant ones present 240/300° disclinations. Junction BN/AlN [40] /BC2N nanotubes [41] were computed. Other layered materials are: WS2, etc. [42-46]. Pyrolytic nano BxCyNz shows C/BN domains; compound provides materials useful as nanocomposites (NCs)/semiconductor devices enhanced towards oxidation [47-49]. CNTs are inert/difficult to integrate into NCs/electronics.
C-NanoBuds ™ (NT-BUDs, fullerene-functionalized SWNTs) were synthesized [50]; all are semiconductors [51]. GR sparked potential to be ingredient of devices (e.g., single molecule gas sensors, ballistic transistors, spintronic) [52]. It was called mother of all graphitic forms because it can be wrapped into fullerenes, rolled into CNTs and stacked into graphite [53]. It consists of hexagonal arrangement of C-atoms in two-dimensional (2D) honeycomb crystals. It differs from most conventional 3D materials. Basic GR is semimetal/zero-gap semiconductor. Zigzag-edges nature imposes localization of electron density with maximum at the border C-atoms, leading to formation of flat conduction/valence bands near Fermi level. Localization states are spin polarized and in case of ordering electron spin along zigzag edges, GR is established in anti/ferromagnetic phase. The former breaks GR sublatice symmetry that changes its band structure and opens a gap. GR/CNTs show third-order nonlinerity. Electronic properties of semiconductor monolayers are better than the bulk, spawning efforts to create functionalized monolayers of other bonded crystal structures. Higher carrier mobility is achieved via ultra-thin topologies but terminating monolayers with ligands for specific applications, ultra-thin materials are made more sensitive than the bulk for sensors. Solvent selection was analyzed [54-56]. Coronado group examined multifunctional hybrid nanocomposites based on CNTs/chemically modified GR [57-59]. Other 2D materials were analyzed [60-66]. Some GR-fullerene nanobuds (GR-BUDs) [67] are calculated magnetic [68].
In earlier publications SWNT [69-74] /(BC2N/BN-)SWNC [75-78] bundlet, GR columnlet [79] cluster models, Sc/GR clusters polarizability and GR1/2-cation interactions [80] were presented. A class of phenomena accompanying solution behaviour is analyzed from a unique point of view taking into account cluster formation. Different structures with delocalized electrons in droplet/bundlet/columnlet models are examined. Based on droplet/bundlet models, GR/GR-BUD columnlet is examined. The aim of the present report is to perform a comparative study of fullerene, SWNT/NT-BUD and GR/GR-BUD. The following section describes the computational method. The next two sections present/discuss results. Finally, the last section summarizes our conclusions.
Computational method
Aggregation changes thermodynamic parameters that displays phase equilibrium and changes solubility. Columnlet is valid when GR sheet number in cluster n << 1. In saturated solution, chemical potentials per sheet for dissolved substance, crystal and clusters match. Cluster free energy depends on its volume, proportional to cluster sheet number n [81]. Our model assumes that clusters present columnlet shape. Gibbs energy Gn for n-sized cluster is:
where G1 and G2 are responsible for contribution to Gibbs energy of molecules placed inside volume and on surface of cluster, respectively, and correspond to formation energies An and -B. The chemical potential μn of a cluster of size n is:
where T is absolute temperature and Cn, concentration of n-sized cluster. With (1) it results:
where G1 and G2 are expressed in temperature units. In saturated sheet solution, cluster-size distribution function is determined via equilibrium condition linking clusters of specified size with solid phase, which corresponds to equality between chemical potentials for sheets incorporated into clusters of any size and crystal, resulting in the expression for the distribution function in a saturated solution:
where A is equilibrium difference between sheet interaction energies with its surroundings in solid phase and cluster volume, B, similarly on cluster surface and gn, statistical weight of n-sized cluster. One neglects gn(n,T) dependences in comparison with exponential (4), which normalization:
requires A < 0, and C is solubility in relative units. As n << 1, normalization (5) results:
where is g n cluster statistical weight averaged over n that makes major contribution to integral (6) and C0, sheet molar fraction. The A, B and C0 were taken from C60 in hexane/toluene/CS2 (A = 320K, B = 970K, C0 = 5•10-8). Correction takes into account packing efficiencies of C60/sheet:
and (sheet) andwhere ηsph = π/3(2)1/2 and ηcyl = π/2(3)1/2 are spheres (facecentred cubic, FCC) and cylinder packing efficiencies, respectively. Distribution-function dependences on concentration/temperature lead to sheet thermodynamic/kinetic parameters. For unsaturated solution, distribution function is obtained by clusters equilibrium condition. From Eq. (4) distribution function vs. concentration is:
where λ depends on concentration and is determined by normalization condition:
where C0 defines absolute concentration: C0 = 10-4mol•L-1 is found requiring saturation in Eq. (9). The formation energy of n-sized cluster results:
Using the distribution function one obtains the heat of solution per mole of dissolved sheet:
where NA is the Avogadro number and λ depends on solution total concentration by normalization condition (9). The solute diffusion coefficient results:
where D0 is the diffusion coefficient of a unit that was taken equal to that of C60 in toluene D0 = 10-9m2•s-1; Eqs. (1)-(12) are modelled in a home-built program available from authors. A droplet cluster model of C60 is proposed following modified Eqs. (1')-(12'):
A bundlet cluster model of SWNT and NT-BUD is proposed following customized Eqs. (1'')-(12''):
Calculation results
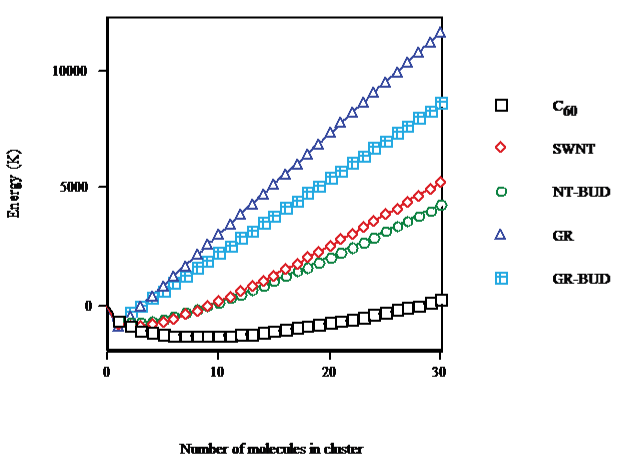
The equilibrium difference between the Gibbs free energies of interaction of an SWNT with its surroundings in solid phase, and cluster volume or on surface (cf. Figure. 1) shows that on going from C60 (droplet) to SWNT (bundlet) the minimum is less marked (68% of C60), causing a lesser number of units in SWNT (nmin ≈ 2) than in C60 clusters (≈8) and a longer abscissa in C60 (nabs ≈ 28) than in SWNT (≈9). Thinner NT-BUD bundles (bundlet) result less stable while wider ones appear more stable than SWNT packages. The minimum of NT-BUD appears 55% of C60. The minimum of GR (columnlet, 67%) is similar to SWNT but with fewer units (≈1) and shorter abscissa (nabs ≈ 3). Shorter GR-BUD stackings (columnlet) result less stable while longer ones appear more stable than GR columns. The minimum of GR-BUD (49% of C60) is alike NT-BUD.
Figure 1: C60/SWNT/NT-BUD/GR/GR-BUD interaction energy with surroundings in cluster volume/surface.
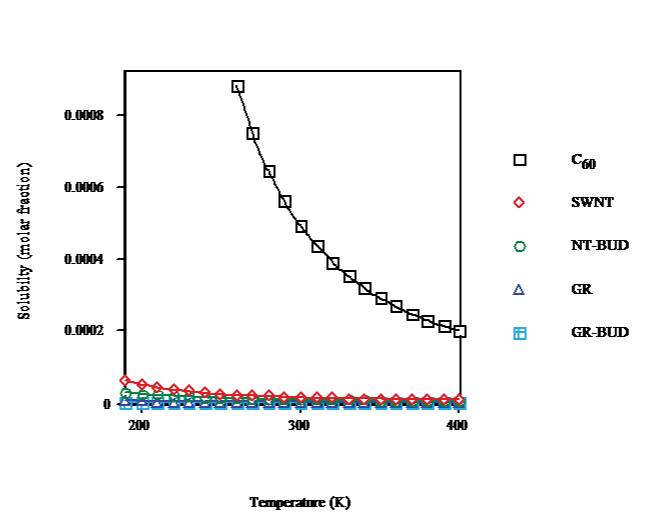
The solubility of SWNT/NT-BUD and GR/GR-BUD vs.temperature (cf. Figure. 2) shows a solubility decay because of cluster formation. At T ≈ 260K, C60-FCC presents a phase transition to simple cubic (SC). The solubility drops with temperature result less marked for SWNT/NT-BUD and even GR/GR-BUD, in agreement with lesser numbers of units in clusters (Figure. 1). At T = 260K from C60 (droplet) to SWNT, NT-BUD (bundlet), GR and GR-BUD (columnlet) the solubility (Figure. 2) decreases to 3%, 2%, 0.3% and 0.1% of C60, respectively.
Figure 2: Temperature dependence of solubility of C60/SWNT/NT-BUD/GR/ GR-BUD.
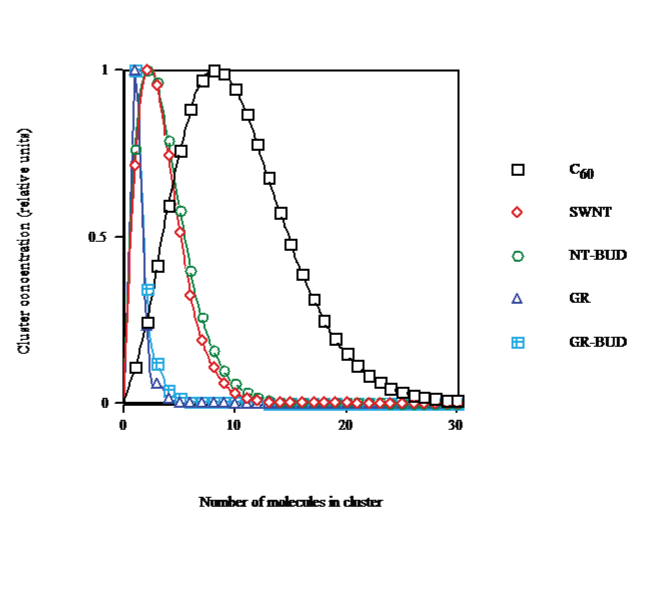
The cluster distribution function by size in CS2, calculated for saturation concentration at solvent temperature T = 298.15K (cf. Figure. 3), shows that on going from C60 (droplet) to SWNT (bundlet) the maximum aggregate size decays from nmax &asymp 8 to &asymp2 and spreading is narrowed, in agreement with lesser number of units in clusters (Figure. 1). The dispersal of NT-BUDs (bundlet) is somewhat enlarged to wider bundles with respect to SWNT. The dissemination of GRs (columnlet) is strongly narrowed in concordance with the fewest units (nmax &asymp 1). The scattering of GR-BUDs (columnlet) is rather increased to longer stacks with regard to GR.
Figure 3: Cluster distribution saturated in CS2 at 298.15K of C60/SWNT/NTBUD/ GR/GR-BUD.
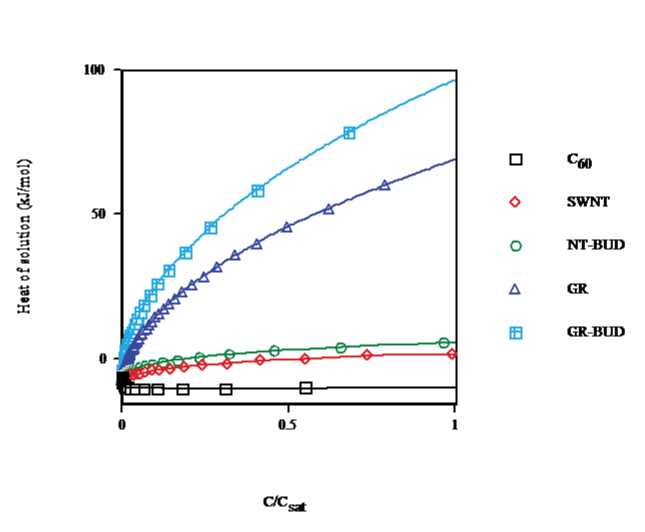
The concentration dependence for the heat of solution in toluene, benzene and CS2 calculated at solvent temperature T = 298.15K (cf. Figure. 4) shows that for C60 (droplet), on going from C < 0.1% of saturated (<n> &asymp 1) to C = 15% (<n> &asymp 7) the heat of solution decays by 73%. In turn, for SWNT (bundlet) the heat of solution rises by 54% in the same range in agreement with a lesser number of units in clusters (Figs. 1 and 3). Moreover, in NT-BUD (bundlet), GR and GR-BUD (columnlet) the heat of solution increases by 98%, 392% and 680%, respectively. The discrepancy between experimental data for the heat of solution of fullerenes, CNT/NT-BUDs and GR/GRBUDs s ascribed to the sharp concentration dependence for the heat of solution.
Figure 4: Heat of solution vs. concentration of C60/SWNT/NT-BUD/GR/GRBUD in toluene/benzene/CS2 at 298.15K.
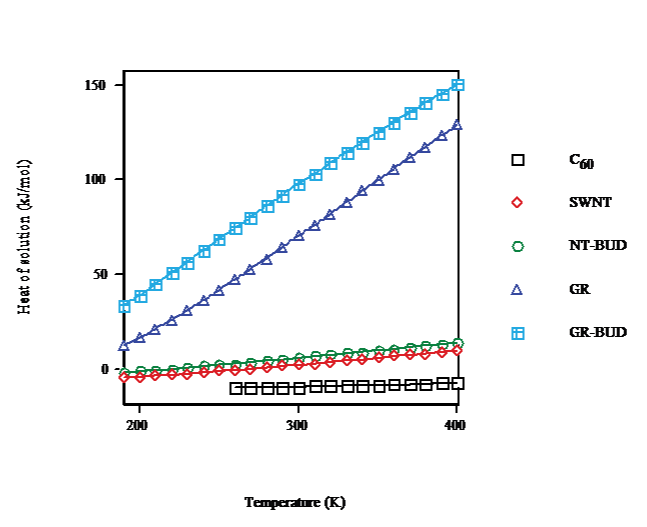
In the temperature dependence for the heat of solution in toluene, benzene and CS2 calculated for saturation concentration (cf. Figure. 5) C60 results are plotted for T > 260K after FCC/SC transition. For C60 (droplet) on going from T = 260K to T = 400K the heat of solution rises 2.7kJ·mol-1. The heat of solution of SWNT (bundlet) increases 10.4kJ·mol-1 in the same range and becomes endergonic. For NTBUD (bundlet) the heat of solution augments 11.3kJ·mol-1 similarly endergonic. Moreover, GR and GR-BUD (columnlet) heats of solution enlarge 82 and 76kJ·mol-1, respectively, likewise endergonic.
Figure 5: Heat of solution vs. temperature of C60/SWNT/NT-BUD/GR/GRBUD in toluene/benzene/CS2 for saturation.
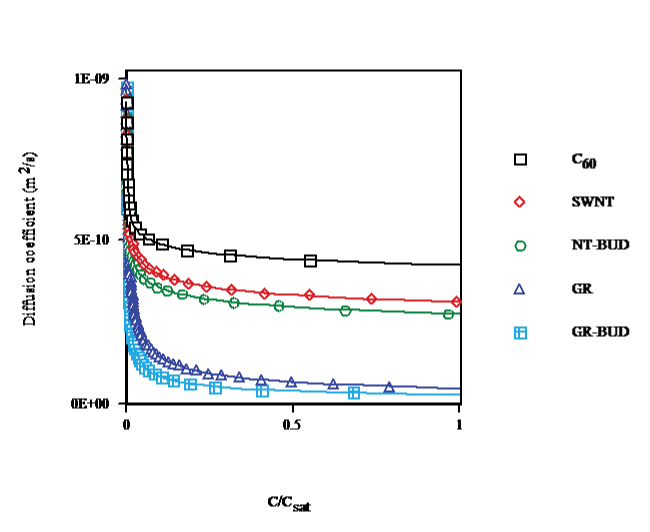
The diffusion coefficient vs. concentration in toluene at T = 298.15K (cf. Figure. 6) shows that cluster formation, close to saturation, decreases the diffusion coefficients by 56%, 69%, 73%, 95% and 97% for C60 (droplet), SWNT, NT-BUD (bundlet), GR and GR-BUD (columnlet), respectively, compared with (C60)1. Diffusion coefficients of SWNT, NT-BUD, GR and GR-BUD decay by 29%, 37%, 88% and 93% contrasted with (C60)n in agreement with lesser number of units in clusters.
Figure 6: Diffusion coefficient vs. concentration of C60/SWNT/NT-BUD/GR/GR-BUD in toluene at 298.15K.
Discussion
For a long time and, because of the fact that some theoretical works established that the long-range crystalline order was impossible in a strictly 2D material, GR was considered as only a reference structure that is found in the origin of other type of stable structures with which one is more familiarized, e.g., CNTs, fullerenes or simply Cgraphite itself [82]. Not by the fact that it was considered as a hypothetical material, it left of being in the mind of some researchers. The first and practically unique intentions of obtaining GR were based on chemical exfoliation where Cgraphite, adequately intercalated, could present considerably separated GR sheets. The compound so formed resulted, however, of scarce interest.
From purely geometrical considerations the columnlet (GR/GRBUD), bundlet (SWNT/NT-BUD) and droplet (fullerene) cluster models predict different behaviours. (1) Spheres (droplet) pack in three dimensions (3D), while cylinders (bundlet) do equivalently to circles in 2D and sheets (columnlet) stack against 1D. The C60 clusters can be greater than SWNT/NT-BUD bundles than GR/GR-BUD stacks, because of C60 > SWNT/NT-BUD > GR/GR-BUD additional curvatures and dimensions. (2) The co-ordination numbers are: CNspheres = 12, CNcylinders = 6 and CNsheets = 2. As surface affects energy [Eqs. (10), (10') and (10'')] on changing the number of atoms the clusters should present discontinuities in areas and stabilities, especially about the corresponding co-ordination numbers. Consequently a discontinuity is expected between closed (C60)13 and open (C60)14 (droplet); the same happens between stopped up SWNT/NT-BUD7 and ajar SWNT/NT-BUD8 (bundlet), and connecting congested GR/GR-BUD3 and unlocked GR/GR-BUD4 (columnlet), which different sizes are in concordance with C60 > SWNT/NT-BUD > GR/GR-BUD extra curvatures and dimensions. (3) Smaller clusters are of the least consideration in columnlet, bundlet and droplet models because all three approaches are valid when n » 1 unit. (4) It has not escaped our notice that aggregates near (C60)13, SWNT/NT-BUD7 and GR/GRBUD3 could be representative of the droplet, bundlet and columnlet models, respectively, with different sizes in agreement with C60 > SWNT/NT-BUD > GR/GR-BUD added curvatures and dimensions. However, all our calculations were performed with the whole size distribution. (5) Because spherical (2D-curved) C60 is more reactive than cylindrical (1D-bended) SWNTs than sheet (straight) GR, a greater dispersion in the results of C60 cluster size (n ≠ 13) is expected, with regard to lesser reactive SWNTs that are waited more uniform in SWNTn (n ~ 7) and least reactive GRs that are anticipated more consistent in GRn (n ≈ 3). In addition C60 is more soluble than SWNTs than GR in organic solvents. (6) The GR is strongly influenced by the materials it comes into contact with, whether solid, liquid or gas. (7) Strictly 2D (single layer) GR is rarely pristine since it contains a number of impurities, C or foreign ad-atoms, vacancies, etc., and the finite crystalline size and support-related effects, e.g., conformality, wrinkles, etc. For a group of potential applications the presence of those defects provides interesting properties related to the spin phenomena, for advanced nanoelectronics and to make possible the attachment of specific molecules. (8) In the investigation at the atomic scale of the impact that atomic defects have on the structural, electronic and magnetic properties of GR layers grown on different materials the pure bidimensionality of GR gives to these defects a critical role. (9) The study of the coupling of GR with its local environment is absolutely critical to be able to integrate it in tomorrow's electronic devices. (10) The atomically thin single-crystal membranes offer ample scope for fundamental research and new technologies, whereas the observed corrugations in the third dimension may provide subtle reasons for the stability of 2D crystals.
The microscopic dimensional considerations above present macroscopic effects. In a linear chain, for a linear model the square fluctuation is proportional to the distance because the amplitude of the fluctuation rises with the squared remoteness. It is because of thiscircumstance that one should attribute the origin of the qualitative distinction that exists between the solid and liquid states. In a liquid,the coherence is conserved at only long distances while naturally the neighbouring atoms preferably form the arrangements of minimalenergy. In the 1D case, the difference between solid and liquid will be only quantitative and instead of a well-determined fusion point there will be a continuum passing.
Conclusions
From the discussion of the present results the following conclusions can be drawn.
- The nanoworld structural diversity is a consequence of its quantum nature. Several criteria reduced the analysis to a manageable number of magnitudes, viz. closeness, curvature, dimension and efficiency. Our non-computationally intensive approach, i.e., object clustering plus propertyprediction, assessed reliability. Type, dimensions and producer selection of fullerenes, nanotubes and graphenes must be chosen to ensure the transfer of methods developed between laboratories. Our interaction energy parameters for nanobuds are taken from C60. For nanotube bud an C60/tube intermediate behaviour was expected. However, nanotubebud properties result closer to tubes. Thinner nanotube-bud bundles appear less stable but wider ones are more stable than tube packages.
- Association energy parameters of nanographene are obtained from C60. A nanotube-bud behaviour or further was expected. For Cgraphene nanobud an C60/Cgraphene in-between behaviour as anticipated. Notwithstanding, nanobud features appear closer to Cgraphene. Shorter nanobud stacks result less stable but longer ones appear more stable than Cgraphene columns. The solubility decays with temperature result smaller for Cgraphene/bud than nanotube/bud than C60, in agreement with lesser numbers of units in clusters. The discrepancy between experimental data for the heat of solution of fullerenes, nanotubes, graphenes and their buds is ascribed to the sharp concentration dependence for the heat of solution. The diffusion coefficient drops with temperature result greater for Cgraphene/bud than nanotube/bud than C60, corresponding to lesser number of units in aggregates.
- Some systems are dominated by the isolated pentagon rule, some others are not. Further work will explore similar nanostructures nature: generalization to systems more complex; e.g., a way of bypassing weak homonuclear bonding exists in closed BxNx (involving replacement of 5-membered by 4-ring B2N2 with heteroatom alternation), BN/AlN tubes/heterojunctions, silicene, germanene and carbine. The C-nanostructures are more controllable while heterostructures present richer behaviour, especially for transtition-metal compounds, showing lubricant and electronic uses.
Acknowledgments
The authors want to dedicate this manuscript to Dr. Luis Serrano- Andrés, who was greatly interested in this research and would have loved to see its conclusion.
References
- Faraday M. The Bakerian Lecture: Experimental relations of gold (and other metals) to light. Philos Trans R Soc London. 1857; 147: 145-181.
- Murphy CJ, Thompson LB, Alkilany AM, Sisco PN, Boulos SP, Sivapalan ST, et al. The many faces of gold nanorods. J Phys Chem Lett. 2010; 1: 2867-2875.
- Balaban AT, Klein DJ, Liu X. Graphitic cones. Carbon. 1994; 32: 357-359.
- Klein DJ. Topo-combinatoric categorization of quasi local graphitic defects. Phys Chem Chem Phys. 2002; 4: 2099-2110.
- Klein DJ, Balaban AT . The eight classes of positive-curvature graphitic nanocones. J Chem Inf Model. 2006; 46: 307-320.
- Klein DJ. Aromaticity via Kekule structures and conjugated circuits. J Chem Educ. 1992; 69: 691-694.
- Misra A, Klein DJ, Morikawa T . Clar theory for molecular benzenoids. J Phys Chem A. 2009; 113: 1151-1158.
- Misra A, Schmalz TG, Klein DJ . Clar theory for radical benzenoids. J Chem Inf Model. 2009; 49: 2670-2676.
- Balaban AT, Klein DJ. Claromatic carbon nanostructures. J Phys Chem C. 2009; 113: 19123-19133.
- Klein DJ, Balaban AT. Clarology for conjugated carbon nano structures: Molecules, polymers, graphene, defected graphene, fractal benzenoids, fullerenes, nano tubes, nano cones, nano tori, etc. Open Org Chem J. 2011; 5: 27-61.
- Tamura R, Tsukada M . Electronic states of the cap structure in the carbon nanotube. Phys Rev B Condens Matter. 1995; 52: 6015-6026.
- Kim P, Odom TW, Huang J L, Lieber CM. Electronic density of states of atomically resolved single-walled carbon nanotubes: Van Hove singularities and end states. Phys Rev Lett. 1999; 82: 1225-1228.
- Carroll DL, Redlich P, Ajayan PM, Charlier J C, Blase X, de Vita A, Car R. Electronic structure and localized states at carbon nanotube tips. Phys Rev Lett. 1997; 78: 2811-2814.
- Krishnan A, Dujardin E, Treacy MMJ, Hugdahl J, Lynum S, Ebbesen TW. Photoisomerization in dendrimers by harvesting of low-energy photons. Nature (London). 1997; 388: 451-454.
- Kroto HW. The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70. Nature (London). 1987; 329: 529-531.
- Han J, Jaffe R. Energetics and geometries of carbon nanocone tips. J Chem Phys. 1998; 108: 2817-2823.
- Tagmatarchis N, Maigné A, Yudasaka M, Iijima S . Functionalization of carbon nanohorns with azomethine ylides: towards solubility enhancement and electron-transfer processes. Small. 2006; 2: 490-494.
- Pagona G, Sandanayaka ASD, Araki Y, Fan J, Tagmatarchis N, Charalambidis G, et al. Covalent functionalization of carbon nanohorns with porphyrins: Nanohybrid formation and photoinduced electron and energy transfer. Adv Funct Mater. 2007; 17: 1705-1711.
- Cioffi C, Campidelli S, Brunetti FG, Meneghetti M, Prato M . Functionalisation of carbon nanohorns. Chem Commun (Camb). 2006; : 2129-2131.
- Cioffi C, Campidelli S, Sooambar C, Marcaccio M, Marcolongo G, Meneghetti M, Paolucci et al. Synthesis, characterization, and photoinduced electron transfer in functionalized single wall carbon nanohorns. J Am Chem Soc. 2007; 129: 3938-3945.
- Pagona G, Fan J, Tagmatarchis N, Yudasaka M, Iijima S . Cone-end functionalization of carbon nanohorns. Chem Mater. 2006; 18: 3918-3920.
- Zhu J, Kase D, Shiba K, Kasuya D, Yudasaka M, Iijima S et al. Binary nanomaterials based on nanocarbons: A case for probing carbon nanohorns' biorecognition properties. Nanoletters. 2003; 3: 1033-1036.
- Pagona G, Sandanayaka AS, Araki Y, Fan J, Tagmatarchis N . Electronic interplay on illuminated aqueous carbon nanohorn-porphyrin ensembles. J Phys Chem B. 2006; 110: 20729-20732.
- Pagona G, Fan J, Maigne A, Yudasaka M, Iijima S, Tagmatarchis N. Aqueous carbon nanohorn-pyrene-porphyrin nanoensembles: Controlling charge-transfer interactions. Diamond Relat Mater. 2007; 16: 1150-1153.
- Xia X, Jelski DA, Bowser JR, George TF. MNDO study of boron-nitrogen analogues of buckminsterfullerene. J Am Chem Soc. 1992; 114: 6493-6496.
- Silaghi-Dumitrescu I, Haiduc I, Sowerby DB. Fully inorganic (carbon-free) fullerenes? The boron-nitrogen case. Inorg Chem. 1993; 32: 3755-3758.
- Hamilton EJ, Dolan SE, Mann CM, Colijn HO, McDonald CA . Preparation of amorphous boron nitride and its conversion to a turbostratic, tubular form. Science. 1993; 260: 659-661.
- Hamilton EJM, Dolan SE, Mann CM, Colijn HO, Shore SG. Preparation of amorphous boron nitride from the reaction of haloborazines with alkali metals and formation of a novel tubular morphology by thermal annealing. Chem Mater. 1995; 7: 111-117.
- Loiseau A, Willaime F, Demoncy N, Hug G, Pascard H . Boron nitride nanotubes with reduced numbers of layers synthesized by arc discharge. Phys Rev Lett. 1996; 76: 4737-4740.
- Rubio A, Corkill JL, Cohen ML . Theory of graphitic boron nitride nanotubes. Phys Rev B Condens Matter. 1994; 49: 5081-5084.
- Bourgeois L, Bando Y, Shinozaki S, Kurashima K, Sato T . Boron nitride cones: structure determination by transmission electron microscopy. Acta Crystallogr A. 1999; 55: 168-177.
- Bourgeois L, Bando Y, Han WQ, Sato T. Structure of boron nitride nanoscale cones: Ordered stacking of 240° and 300° disclinations. Phys Rev B. 2000; 61: 7686-7691.
- Terauchi M, Tanaka M, Suzuki K, Ogino A, Kimura K. Production of zigzag-type BN nanotubes and BN cones by thermal annealing. Chem Phys Lett. 2000; 324: 359-364.
- Mota R, Machado M, Piquini P. Structural and electronic properties of 240° nanocones. Phys Status Solidi C. 2003; 0: 799-802.
- Machado M, Piquini P, Mota R. Energetics and electronic properties of BN nanocones with pentagonal rings at their apexes. Eur Phys J D. 2003; 23: 91-93.
- Machado M, Piquini P, Mota R. Electronic properties of selected BN nanocones. Mater Charact. 2003; 50: 179-182.
- Machado M, Mota R, Piquini P. Electronic properties of BN nanocones under electric fields. Microelectron J. 2003; 34: 545-547.
- Machado M, Piquini P, Mota R. Charge distributions in BN nanocones: Electric field and tip termination effects. Chem Phys Lett. 2004; 392: 428-432.
- Machado M, Piquini P, Mota R . The influence of the tip structure and the electric field on BN nanocones. Nanotechnology. 2005; 16: 302-306.
- Thesing LA, Piquini P, Kar T. Theoretical investigation on the stability and properties of III-nitride nanotubes: BN-AlN junction. Nanotechnology. 2006; 17: 1637-1641.
- Miyamoto Y, Rubio A, Cohen ML, Louie SG . Chiral tubules of hexagonal BC2N. Phys Rev B Condens Matter. 1994; 50: 4976-4979.
- Tenne R, Margulis L, Genut M, Hodes G. Polyhedral and cylindrical structures of tungsten disulphide. Nature. 1992; 360: 444-446.
- Margulis L, Salitra G, Tenne R, Talianker M. Nested fullerene-like structures. Nature. 1993; 365: 113-114.
- Wang QH, Kalantar-Zadeh K, Kis A, Coleman JN, Strano MS . Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat Nanotechnol. 2012; 7: 699-712.
- Weng-Sieh Z, Cherrey K, Chopra NG, Blase X, Miyamoto Y . Synthesis of BxCyNz nanotubules. Phys Rev B Condens Matter. 1995; 51: 11229-11232.
- Chopra NG, Luyken RJ, Cherrey K, Crespi VH, Cohen ML . Boron nitride nanotubes. Science. 1995; 269: 966-967.
- Terrones M, Benito AM, Manteca-Diego C, Hsu WK, Osman OI, Hare JP, et al. Pyrolytically grown BxCyNz nanomaterials: Nanofibres and nanotubes. Chem Phys Lett. 1996; 257: 576-582.
- Kohler-Redlich P, Terrones M, Manteca-Diego C, Hsu WK, Terrones H, Rühle M, et al. Stable BC2N nanostructures: Low-temperature production of segregated C/BN layered materials. Chem Phys Lett. 1999; 310: 459-465.
- Madden JD . Materials science. Stiffer than steel. Science. 2009; 323: 1571-1572.
- Nasibulin AG, Pikhitsa PV, Jiang H, Brown DP, Krasheninnikov AV . A novel hybrid carbon material. Nat Nanotechnol. 2007; 2: 156-161.
- Wu X, Zeng XC . First-principles study of a carbon nanobud. ACS Nano. 2008; 2: 1459-1465.
- Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y . Electric field effect in atomically thin carbon films. Science. 2004; 306: 666-669.
- Geim AK, Novoselov KS . The rise of graphene. Nat Mater. 2007; 6: 183-191.
- Hernandez Y, Nicolosi V, Lotya M, Blighe FM, Sun Z . High-yield production of graphene by liquid-phase exfoliation of graphite. Nat Nanotechnol. 2008; 3: 563-568.
- Khan U, O'Neill A, Lotya M, De S, Coleman JN . High-concentration solvent exfoliation of graphene. Small. 2010; 6: 864-871.
- Zhang X, Coleman AC, Katsonis N, Browne WR, van Wees BJ . Dispersion of graphene in ethanol using a simple solvent exchange method. Chem Commun (Camb). 2010; 46: 7539-7541.
- Bosch-Navarro C, Coronado E, Martí-Gastaldo C, Sánchez-Royo JF, Gómez MG . Influence of the pH on the synthesis of reduced graphene oxide under hydrothermal conditions. Nanoscale. 2012; 4: 3977-3982.
- Bosch-Navarro C, Coronado E, Martí-Gastaldo C. Controllable coverage of chemically modified graphene sheets with gold nanoparticles by thermal treatment of graphite oxide with N,N dimethylformamide. Carbon. 2013; 54: 201-207.
- Bosch-Navarro C, Busolo F, Coronado E, Duan Y, Martí-Gastaldo C, Prima-Garcia H. Influence of the covalent grafting of organic radicals to graphene on its magnetoresistance. J Mater Chem C. 2013; 1: 4590-4598.
- Coronado E, Galán-Mascarós JR, Martí-Gastaldo C, Ribera A. Insertion of magnetic bimetallic oxalate complexes into layered double hydroxides. Chem Mater. 2006; 18: 6112-6114.
- Gadet V, Mallah T, Castro I, Verdaguer M, Veillet P. High-Tc molecular-based magnets: A ferromagnetic bimatallic chromium(III)-nickel(II) cyanide with Tc = 90K. J Am Chem Soc. 1992; 114: 9213-9214.
- Coronado E, Martí-Gastaldo C, Navarro-Moratalla E, Ribera A, Blundell SJ . Coexistence of superconductivity and magnetism by chemical design. Nat Chem. 2010; 2: 1031-1036.
- Fang L, Wang Y, Zou PY, Tang L, Xu Z, Chen H, et al. Fabrication and superconductivity of NaxTaS2 crystals. Phys Rev B. 2005; 72: 14534-1-8.
- Coronado E, Martí-Gastaldo C, Navarro-Moratalla E, Burzurí E, Camón A . Hybrid magnetic/superconducting materials obtained by insertion of a single-molecule magnet into TaSâ‚‚ layers. Adv Mater. 2011; 23: 5021-5026.
- Abellán G, Carrasco JA, Coronado E . Room temperature magnetism in layered double hydroxides due to magnetic nanoparticles. Inorg Chem. 2013; 52: 7828-7830.
- Novoselov KS, Jiang D, Schedin F, Booth TJ, Khotkevich VV . Two-dimensional atomic crystals. Proc Natl Acad Sci U S A. 2005; 102: 10451-10453.
- Wu X, Zeng XC . Periodic graphene nanobuds. Nano Lett. 2009; 9: 250-256.
- Wang M, Li CM . Magnetic properties of all-carbon graphene-fullerene nanobuds. Phys Chem Chem Phys. 2011; 13: 5945-5951.
- Torrens F, Castellano G. Cluster origin of the solubility of single-wall carbon nanotubes. Comput Lett. 2005; 1: 331-336.
- Torrens F, Castellano G. Cluster nature of the solvation features of single-wall carbon nanotubes. Curr Res Nanotechn. 2007; 1: 1-29.
- Torrens F, Castellano G. Effect of packing on the cluster nature of C nanotubes: An information entropy analysis. Microelectron J. 2007; 38: 1109-1122.
- Torrens F, Castellano G. Cluster origin of the transfer phenomena of single-wall carbon nanotubes. J Comput Theor Nanosci. 2007; 4: 588-603.
- Torrens F, Castellano G. Asymptotic analysis of coagulation-fragmentation equations of carbon nanotube clusters. Nanoscale Res Lett. 2007; 2: 337-349.
- Torrens F, Castellano G . (Co-)solvent selection for single-wall carbon nanotubes: best solvents, acids, superacids and guest-host inclusion complexes. Nanoscale. 2011; 3: 2494-2510.
- Torrens F, Castellano G. Cluster nature of the solvent features of single-wall carbon nanohorns. Int J Quantum Chem. 2010; 110: 563-570.
- Torrens F, Castellano G. Bundlet model for single-wall carbon nanotubes, nanocones and nanohorns. Int J Chemoinf Chem Eng. 2012; 2: 48-98.
- Torrens F, Castellano G. Bundlet model of single-wall carbon, BC2N and BN nanotubes, cones and horns in organic solvents. J Nanomater Mol Nanotech. 2013; 2: 1000107-1-9.
- Torrens F, Castellano G. Solvent features of cluster single-wall C, BC2N and BN nanotubes, cones and horns. Microelectron Eng. 2013; 108: 127-133.
- Torrens F, Castellano G . C-nanostructures cluster models in organic solvents: Fullerenes, tubes, buds and graphenes. J Chem Chem Eng. 2013; 7: 1026-1035.
- Torrens F, Castellano G (in press) Elementary polarizability of Sc/fullerene/graphene aggregates and di/graphene-cation interactions. J Nanomater Mol Nanotech.
- Bezmel'nitsyn VN, Eletskii AV, Okun' MV. Fullerenes in solutions. Physics-Uspekhi. 1998; 41: 1091-1114.
- Peierls R. Quelques propriétés typiques des corps solides. Ann Inst Henri Poincaré. 1935; 5: 177-222.