Computational Models in Neuroscience: How real are they? A Critical Review of Status and Suggestions

    

    

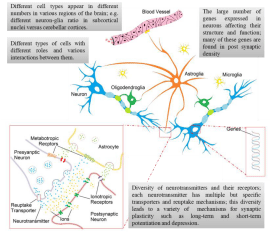
    Figure 1:  A schematic diagram of some of the important aspects of the nervous system that have been considered in modeling, however not addressed properly
including different cell types (neuronal and glial) and their numbers in different areas of the brain, diversity of neurotransmitters and their transporters and receptors
and various gene expressions in neurons.
Cells: Numbers, Types, and Ratios.
    
    

The nervous system is a huge complex network comprising of different cells, with different shapes and sizes that play diverse roles in its function. The human brain is unique in its several characteristics and comprises of over 86 billion neurons with approximately the same number of non-neuronal cells, called glia [14-16]. These neurons are connected to each other through 100 to 500 trillion synapses [17]. Other primate’s brain, such as owl monkey, capuchin monkey, chimpanzee and gorilla also include billions to tens of billions of neurons [15,18]. Modeling studies have an obvious limitation as data from individual cells and also different cell types of human brain is not available due to experimental limitations (even if it was available, we would not know how to process and interpret this huge amount of data). On the other hand, in large network models of different brain areas, these studies drastically downscale the size of the network due to computational limitations which may affect the reliability of the results of such models. For example, the downscaling has been mentioned to be of great importance in interpreting the results of computational models of neurogenesis and its role in learning and memory as the size of the network (number of computational units) has a major effect on network capacity in learning and memory [19].

Additionally, models of the nervous system usually consider a single type of cell or interactions of two or three relevant types of cells. However, as mentioned earlier, in reality, the nervous system comprised of extensive and complex networks of various types of neurons, interneurons and glial cells. Especially, in this regard, considering the active role of astroglia in various neuronal functions and synaptic plasticity, neuronal models without considering neuronglia interactions pose major limitations in understanding the neurobiological facts at the cellular level [1,20,21]. Interestingly, employing astrocytes, even in Artificial Neural Network, or Artificial Neuron- Glia Networks, improves the performance of the network [21].

There are interspecies variations of neuronal and glial number, function and structure [22]. For instance, the ratio of cells, such as neuron verses glia, differs in a high proportion across species [23]. In Caenorhabditis elegans there are 302 neurons and only 56 glial and associated support cells [24], while in leech, a typical ganglion is composed of 25 to 30 neurons and only one astrocyte [23]. In addition, astrocytes and neurons are represented in a ratio of 1:3 in the cortex of lower mammals such as rats and mice while in the human cerebral cortex, there are 1.4 astrocytes for every neuron [25]. Modeling studies usually fail to address these differences which are of great importance due to lack of a systematic approach for correlating data from different species [13]. Additionally, the ratio of different cell types and their connections are different in, and specific to various regions of the brain. In the human brain, the glia to neuron ratio in subcortical nuclei can be as high as 17:1 in the thalamus [26] compared to the relatively small combined number of glial cells reported for the cerebral [27] and cerebellar cortices [28]. These differences in the ratio of neuron and glia in different regions of the brain have also been reported in animals such as mice [29] and rats [30]. However, modeling studies sometimes do not specify the part or specific region of the brain to which the model with the fixed ratios applies. For instance, some studies proposed a model for neuronastrocyte network [31,32], however, failed to explain which part of human brain they were modeled, although the ratio of Neuron verses Glia is different in various regions of brain [33].

Synapses, Neurotransmitters and Receptors

Neural networks are complex structures including a large number of synapses. For example, a CA1 pyramidal cell in rat hippocampus receives around 30,000 excitatory and 1,700 inhibitory inputs [34] with different ratios of excitatory versus inhibitory synapses in different areas of soma, axon and dendrites [35]. These structural differences are thought to affect the functional aspects of pyramidal neurons, especially the synaptic integration [35]. Moreover, the number of these connections is not invariant and changes due to neural branching and synaptogenesis [36-39]. Also, variable is the strength of these synapses because of variations in the level of plasticity at individual synapses. Various mechanisms and types of synaptic plasticity have been thoroughly studied such as long-term and short-term potentiation and depression [40,41]. Moreover, the activity dependence of synapses, either depressed or facilitated during continuous activity, has been shown to play an important role in functionality of various neuronal microcircuits, especially in neocortex and spinal cord. This activity dependence is itself subjected to modulation by some neurotransmitters such as serotonin by a process called meta-modulation [42]. The structural changes in synapses have also been investigated through the morphological changes and reorganization of postsynaptic density (PD), the localized area under the postsynaptic membrane containing several proteins. It has been suggested that the reorganization of PD is the underlying cause for long-term potentiation and depression and may even have some role in synaptogenesis [43,44]. Different roles of PD proteins in the structure and function of synapses have resulted in linking various neurological disorders such as autism and schizophrenia to their mutations and dysfunctions [44,45]. Moreover, neurons can also make synapses upon themselves, called autapse. These feedback circuits that are, for example, present in about 80% of cortical pyramidal neurons, have been reported to play some role in maintaining activity and controlling the precision of spike timing in neurons [46,47]. Several modeling studies have investigated the function of autapse in neuronal activity and have shown its role in information regulation and firing pattern transition [47,48].

These variations in number, structural complexity and strength of synapses are thought to be the underlying mechanisms of learning and memory [39-41,49]. All these factors added to the already existing complexity of modeling of neural networks. Application of random variables for connections within the models of neural network has been employed to handle the variations in numbers and plasticity of synapses [2], however, experimental results of neuroscience research show that the topology of brain network is much more complex and statistically far from random networks [50]. Furthermore, these network models of different regions of the brain not only include a fixed number of synapses, but also employ a single phenomenological model -black box model -of a specific mechanism for synaptic plasticity (usually Spike-Time-Dependent-Plasticity (STDP)) for the whole network [51-53]. However, neurophysiological observations clearly show the existence of several types of plasticity mechanisms even within different layers of the same region of the brain [54] which leads to limited applicability of STDP when employed as a unifying framework for the synaptic plasticity [55]. Moreover, the widespread classic STDP model, including its simplified dependence on timing of spikes in a pair of pre and post synaptic neurons fails to explain a wide range of experimental observations related to the dependence of plasticity on frequency, voltage, dendritic location, etc. [56]. At the same time, due to the lack of needed technology for detailed monitoring of molecular basis for synaptic plasticity, some biophysical models have been constructed for a specific type of synaptic plasticity such as short-term plasticity [57], N-Methyl-DAspartate (NMDA) receptor dependent plasticity [58], etc., in order to provide some insight into underlying interactions of different compartments within the synapses. However, these limited though realistic biophysical models have not been used in network models of brain function because of the huge amount of computational effort they impose.

Regarding chemical synapses, the diversity of neurotransmitters and their receptor subtypes involved in various aspects of neuronal function is very high. Specific populations of neurons synthesize particular neurotransmitter and express its receptors. So far more than one hundred molecules have been identified that function as neurotransmitters in the human brain. These neurotransmitters can be classified based on various criteria such as size - small-molecule neurotransmitters and neuropeptides, or kind of post-synaptic effect -excitatory and inhibitory [59]. Furthermore, each neurotransmitter is usually associated with several ionotropic and/or metabotropic receptors, resulting in an even greater number of receptors within the brain [60]. For example: Dopaminergic neurons synthesize dopamine and express their receptors while there are five subtypes of dopamine receptors in mammals with different excitatory and/or inhibitory effects [61]. Neurotransmitter serotonin has more than fourteen types of receptors present in the central nervous system [62]. Moreover, every neurotransmitter has its own transporter system, inactivation and reuptake mechanism that is specific to it and influences its functional aspect. For instance, glutamate, as the most prominent and main excitatory neurotransmitter of the human brain is synthesized (by two different mechanisms), transported to synaptic cleft (by at least three different transporters) and then removed from the synaptic cleft (by five different transporters) in a series of events called glutamate-glutamine cycle [59]. The same process of synthesis, transportation and reuptake is different for Gamma-Aminobutyric Acid (GABA) as the main inhibitory neurotransmitter of brain [59]. Although a lot of modeling studies have included different neurotransmitters and their receptors [58,63-65], these studies usually do not consider the various aspects of the neurotransmission such as different types of neurotransmitters and different transporter systems and receptor subtypes for each neurotransmitter.

Genetic Considerations

Neurons, on average, express more than 14000 genes [66]. Many of these genes are exclusively expressed in different types of neurons and in different regions of the brain, while some are specific for the proteins found in post synaptic density [67-69]. Even neurons of the same type that appear to be morphologically similar show marked differences in patterns of gene expression [70]. Additionally, a similar trend of gene expression is seen in astroglial cells [71].

The important role of genes in structural development and therefore function of brain neural networks, calls for neural modeling at the molecular and gene level [72]. During the past decade, Computational Neurogenetics models [72] have been introduced that incorporate interactions between genes and their effect on neuronal functions and brain activity at the network level. In a series of studies, this approach was used for several inquiries such as the effect of a specific gene knockout on gene regulatory network and therefore network dynamics [73], and more recently for employing accurate low level molecular models of synaptic transmission and introducing probabilistic computational neurogenetic models [74]. An interesting observation among these modeling studies is that due to complex interactions between genes, deletion or mutation of a single gene may alter the whole network activity in such a way that it cannot be modeled by simple manipulation of high level neuronal parameters as the functional outcome of that genetic variation [73]. These observations show the importance of cellular and subcellular mechanisms on functional aspects of networks of neurons that are usually left out as insignificant or used with little details in modeling studies.

Neurological Diseases

One of the main applications of computational neuroscience has been in the modeling of neurological disorders such as psychiatric disorders, epilepsy, Parkinson’s disease and movement disorders, Huntington’s disease, Alzheimer’s disease, thalamocortical dysrhythmia, lesions and injuries, etc. [75-79]. There are some features that make modeling and simulation studies a valuable alternative in nervous system disease research, such as being inexpensive and free of ethical issues [76]. However, neural models of brain malfunctions mostly provide symbolic descriptions of different behaviors and do not capture the subjective experience which is of great importance in neuropsychiatric disorders [12,76]. Also, the nervous system is not structurally or functionally isolated of other systems such as endocrine and immune systems. Similarly, in several disorders of the nervous system, more than one system is involved in the etiology and pathogenesis, such as multiple sclerosis, epilepsy, amyotrophic lateral sclerosis, etc.

Some examples of neuronal models with their drawbacks and limitations are provided in (Table 1).

Table 1: Examples of models based on different cell types and their limitations.

  

    
Cell type Considered in Model 
    
Comment / Limitation 
    
Reference 
  
  

    
Neuron 
    
Although capable of producing a wide range of behaviors, model’s    parameters lack biophysical relevance and applicability [7].
    
[80]
  
  

    
This model incorporates a “threshold integrator” for two neurons    connected by a functional synapse that only considers frequency-dependent    plasticity.
    
[81]
  
  

    
A large-scale spiking network model of the cerebellum including    conductance-based, Leaky Integrate and Fire (LIF)* model specifically for    representation of the passage of time; However, irrelevant types of neurons    such as basket and stellate cells were omitted.
    
[82]
  
  

    
Glia 
    
A Biophysically realistic model for intracellular Ca2+ wave in glial    network; however, it does not consider any mechanism for regenerative release    of ATP [83].
    
[84]
  
  

    
Neuron and  Glia 
    
Although incorporating a detailed biophysical model for astrocyte, the    neuron model is a phenomenological one, namely Leaky Integrate and Fire (LIF)    model.
    
[3]
  
  

    
Neuron and  Interneuron 
    
Realistic simulation of firing of 22 Types of excitatory and    inhibitory cells of thalamocortical system using the basic Izhikevich neuron    model [80]. However, the model lacks calibration or validation in the    presence of multiple and diverse input signals.
    
[85]
  
  

    
“Point neuron” models including 4-Types of cells (2 neurons and 2    inter-neurons) in a network model of dentate gyrus; Only considers some    specific connections between these cells based on the objective of the study    and disregards others without biophysical relevance.
    
[2]
  
  

    
Neuron, Interneuron and Astrocyte 
    
A biophysically realistic model for calcium dynamics in astrocyte along    with Hodgkin-Huxley (HH) Type** models for neuron (pyramidal) and    interneuron; However, it does not consider the specific geometry of the network    and therefore the spatial propagation of signals and corresponding time    delays.
    
[31]
  
  

    
*LIF is a resistor-capacitor model    with a resetting mechanism of spiking events and a delay for refractory    period. 
      
**HH-Type model includes a    capacitance model of the cell membrane and voltage-dependent currents of    various ions. 
      
 
  

Table 1:  Examples of models based on different cell types and their limitations.

Close

Issues with Terminology Used in Modeling Studies

At the end of this section we will briefly comment on a few examples of neuroscience terminology used in modeling studies. Within the framework of computational modeling studies, the interdisciplinary nature of neuroscience also demonstrates the requirement for collaboration among theorists and experimentalists from various related fields for the purpose of the model being both computationally and physiologically plausible and therefore of use in real biological arena. In this regard, it is notable that some modeling studies have used terminologies that differ from core neuroscience literature and in many instances create confusion for the reader. Some of these terms are obsolete and are rarely used in current neuroscience literature. One example is inappropriate use of biological terminology such as synaptic space [86] or extra synaptic space [87] these are obsolete and incorrect terms, instead of synaptic cleft as an established term in neuroscience [88]. Another example is the use of term glion instead of glial cell [20]. Additionally, ‘glia’ is commonly used for astroglial cells, while it is a general term that encompasses astroglia, microglia, oligodendroglia and other non-neuronal cells of the nervous system. Also, the frequently used incorrect expression tripartite synapses for the connection between presynaptic and postsynaptic neurons and astrocyte [89,90] in modeling studies is not an established terminology used in neuroscience literature.

Modeling Perspective

One of the main aspects of any modeling study is its abstraction level. Different modeling studies incorporate different levels of biological details in their models that determine its general scope [19,91]. In this section, various advantages and disadvantages of abstract and detailed models are discussed. Specifically, within this framework, the multilevel modeling approach that has been successfully employed in some studies is investigated. Also discussed, is the biological correspondence as the major requirement of any modeling study.

Abstraction Level

Black box models, mostly provide an input-output relationship of the system. In spite of their common application in neuronal function modeling, these are certainly a major limitation on the role and impact of models used in the simulation of nervous system function. These simple phenomenological models with low level of details are computationally plausible and easier to analyze [19] and even show great performance in reproducing neuronal activity recorded in experiments [11]. However, these models do not consider various aspects of neuronal, glial, synaptic and network functions. Considering the high level of simplification in these models, an explicit correspondence between model parameters and physical variables is missing. Therefore, these models usually fail to give a useful explanation of the inner interconnections of the variables that are needed for the understanding of the modeled system [92-94].

On the other hand, detailed biophysical models incorporate several measurable physiological variables and therefore can provide good insights into the cellular and sub-cellular mechanisms involved in neuronal dynamics. In practice, these models’ ability in providing insights into the low-level molecular mechanisms of biological phenomena of interest, accompanied by full detailed knowledge and control of the experiment [76], makes them a valuable alternative in the study of the nervous system especially in neurological disorders research. However, these detailed models usually suffer from high dimensionality that can reduce the explanatory aspect of such models regarding the overall dynamical state of the neural system [95]. Furthermore, employing these biophysical models for constructing realistic large network models of whole brain or even specific brain areas requires an extremely large amount of computational resources which are only accessible to specific research centers around the world. In this regard, development of realistic large scale models of the nervous system is the main purpose of one of the multinational major projects launched in Europe in the field of Neuroscience, Human Brian Project (HBP) [96]. HBP has recently reported an in silico reconstruction of the neocortical microcircuitry of the rat brain as the most detailed model of less than a third of cubic millimeter piece of excitable brain tissue to date, containing about 30,000 neurons and 37 million synapses [97]. While the reconstruction did not include many important details such as glia, multiple receptor types, neuromodulation and plasticity, it simulated some of the experimental observations of the brain [97]. However, this project that was ongoing for 10 years and involved a huge amount of funding and computational effort came under criticism for it’s over simplification, limited applicability and even justification necessary for reproducing the reported outcomes [98]. Additionally, an earlier study with much less funding and resources used a 2.5 million neuron model of whole brain with about one billion connections and explored the underlying neuronal mechanisms at several levels for cognitive functions with comparable results [99].

An alternative approach that has been successfully employed to bring together the analytical power of phenomenological models with biophysical descriptive power of detailed models is the multilevel modeling approach in which different models corresponding to different levels, from sub-cellular to whole brain or organism, are constructed for the same phenomenon [95,100]. In order to overcome the limitation of two mentioned levels of modeling, these across-scale models attempt to recognize the relationship between parameters at different levels and their correspondence to existing biological variables. For instance, across-level modeling approach has been extensively incorporated in linking the decline in dopaminergic modulation to age-related increase in neural noise and decrease in the distinctiveness of cortical representations [4]. Another example is the successful application of models of spreading depression from a seizure generating area of brain and linking it to biophysical variables of additional increase in extracellular potassium concentration, indicating pathological process (activation) and potassium buffering indicating the recovery process (inhibition) [101]. Although a systematic method for deriving these multi-level models is still missing, these models can specifically help the integrative capacity of computational models in linking multimodel data, i.e. observations at different levels of organization by experiments (see Figure 2) which has been identified as one of the main challenges of the modern neuroscience [13,102]. This can be of great use in neurological disorders research also as most of these diseases include pathophysiological effects -from genes to behavior -that are usually too complicated to be unified in a single conceptual framework; for example, the specific application of computational models to understand the underlying mechanism of drug-resistant epileptic seizures [103]. Actually, this integrative approach to unifying multilevel data is also attracting an increasing amount of interest in other fields of life sciences [104]. Furthermore, this across-scale approach is more compatible with the widely available computational resources to the researchers in this field.

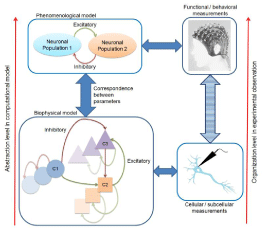
Figure 2: Multi-level method for computational modeling of nervous system. This method integrates experimental observations obtained from different organizational levels (sub-cellular to behavioral) in a unified framework.

    

    

    Figure 2:  Multi-level method for computational modeling of nervous system. This method integrates experimental observations obtained from different organizational
levels (sub-cellular to behavioral) in a unified framework.
    
    

Close

Biological Correspondence

For the model to be applicable, it should be in close correspondence with experimental observations considering its biological plausibility and validation [100,105]. As to biological plausibility, it is noteworthy that usually these models can mimic the experimental measurements in a broad range of values of their parameters that may or may not be in agreement with corresponding physiological values and therefore have biological relevance [91]. For instance, large variations of maximum conductance of voltage-gated currents in a conductancebased model of a single neuron has shown to result in the same state of activity of silent, tonic or bursting [106]. Furthermore, in order to validate the model, it should be used to make experimentally testable predictions and hypotheses; as otherwise, the generalizability of the model (within its specific scope of application corresponding to experimental findings) becomes questionable (see Figure 3). An example is the application of computational models to predict the needed continuous background inhibitory synaptic drive and the excitation by parallel fibers to Purkinje cells for producing a highly irregular simple spike firing seen in vivo that was also confirmed in experimental recordings [107].

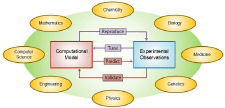
Figure 3: Computational models requirements regarding their correspondence to experimental observations and their multidisciplinary nature that calls for collaborations between experts from various fields, some of which are shown in the figure. Each model should be able to reproduce experimental recordings at some level assured that its parameters fall into physiological range. Also, for validation, the model should be used for experimentally testable predictions.

    

    

    Figure 3:  Computational models requirements regarding their correspondence
to experimental observations and their multidisciplinary nature that calls
for collaborations between experts from various fields, some of which are
shown in the figure. Each model should be able to reproduce experimental
recordings at some level assured that its parameters fall into physiological
range. Also, for validation, the model should be used for experimentally
testable predictions.
    
    

Close

One of the main issues of modern neuroscience that has been specifically addressed in some worldwide projects such as Brain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiative in the US is the technological limitations regarding experimental access to different cell types and subtypes and also dynamic monitoring of neural activity in large scale networks [108]. The predictive power of computational model can play a very important role in guiding the experiments in search for the key parameters in order to make them cost-effective considering the huge number of variables to be considered alongside the limited resources available, and also the expensive nature of experiments [13]. For instance, to investigate neurogenesis, computational models can help in solving the problem of developing behavioral tasks that specifically address the functional role of neurogenesis [19].

Within the framework of computational modeling studies, the interdisciplinary nature of neuroscience also demonstrates the requirement for collaboration among theorists and experimentalists from various related fields [109] (see Figure 3). A main issue in this area could be the different style of thinking among computational modelers, neurologists and experts from other disciplines. This necessitates a transdisciplinary approach from all the parties in expanding their knowledge about each other’s specific methodology [76]. In this regard, neurodynamics has been suggested as a common language that allows both computational and experimental examinations leading to a common framework for linking various behavioral, neural and molecular processes [110]. Obviously, acquiring thorough knowledge in various fields from mathematics and computer science to chemistry and medicine is simply beyond the competence of a single individual or even a few for that matter, and calls for a much higher level of collaboration as can be seen in a number of national and international projects such as BRAIN Initiative in the US and HBP in EU [13,97,108].

Concluding Remarks

So far, different aspects of the computational models of biological and modeling perspectives have been discussed. These are summarized in Figure 4. Additionally, a list of questions addressing some basic considerations regarding the scope and applicability of a model is given in (Table 2).

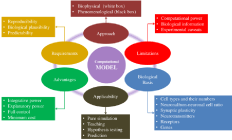
Figure 4: Different aspects of computational neuronal models.

    

    

    Figure 4:  Different aspects of computational neuronal models.
    
    

Close

Table 2: A self-evaluative approach for computational modeling in neuroscience.

  

    
Question / Comment 
  
  

    
1 
    
What are the    objectives of designing the model?
  
  

    
2 
    
What are the types    of cells considered in the model?
  
  

    
3 
    
Which type of    modeling approach is used? White box, black box, or gray box?
  
  

    
4 
    
How many variables    are considered in the model?
  
  

    
5 
    
What are the    functional aspects considered in the model?
  
  

    
6 
    
What is the applied    aspect of the model?
  
  

    
7 
    
What are the    limitations of the model?
  
  

    
8 
    
Is the model good    enough for teaching neuroscience?
  
  

    
9 
    
Is the model just a    simulation?
  
  

    
10 
    
Is there any    predictability accompanied by the model?
  

Table 2:  A self-evaluative approach for computational modeling in neuroscience.

Close

Every model is basically an oversimplification of the reality and no matter how much detail is considered in a model, it will never be a perfect representation of the reality -That is why they are called models [76,100]. In addition, rapid and continuous advancements in the fields of biology and neuroscience lead to discovery of new processes and mechanisms that are then translated into new variables and these then have to be incorporated in the new models to be as near to the reality of the nervous system at different levels. Considering the limited computational power and experimental access, a key feature of any modeling study is the process of leaving out so called unnecessary details [95], which turns out to be a very difficult task in the modeling of the nervous system, considering its multidisciplinary nature. For instance, in computational models of neurological disorders, inappropriate selection of minimal neuronal models can lead to convergence problems, i.e., failure of model in producing pathological effects, which in turn can lead to misleading interpretations [12,76,100]. Development and application of the physiologically justified process of simplification can solve various problems and enhance applicability [111]. However, there is no absolute right level to the extent of details that can be included in a model [106]. Consideration to the intended application, available computational resources and experimental observations in employing a specific level of abstraction are usually taken as a necessary prerequisite for the modeling study of neuronal function [7,112].

Despite all the scientific and technological progress, computational neuroscience is in its early stages of mostly gathering data rather real modeling of the nervous system. Thus, expecting or claiming general one-size-fit-all models seems highly unrealistic at this stage [113]. In reality, diversity and emerging complexity of the nervous system makes it almost impossible to derive such a single universal model in any aspect or level. Studies on single neurological disorders such as epilepsy verify that no such model exists that can cover different types of even a single disease [63,105]. This is the reason why most of the network models of the brain are inspirations of biophysical realism resulting in qualitative explanations of experimental observations, rather quantitative predictions of measurable variables [76]. However, this doesn’t imply that scientists do not explore available resources for more biophysically realistic models. Actually, due to the high complexity of brain dynamics, computational models based on neurobiological principles can play an important role towards incorporating biological details in whole brain models which seems almost impossible in a conceptual framework [13]. As mentioned earlier, considering the limitations of widely accessible computational and experimental power, multilevel modeling can play an effective role in providing some insight into underlying biophysical mechanisms that result in specific high level activity of the brain. This approach can lead to the needed shift from pure reproductions of neuronal activities by models, towards the application of these models for testing the available hypotheses on underlying mechanisms or experimental observations [104,114]. Specially, this is of great importance in modeling studies of neurological disease, if any, future application of these models in the diagnosis and treatment of those diseases is intended. This rare, not to say unique, quality of computational modeling in integrating structural, functional and dynamical properties in nervous system makes it a powerful tool in the area of neuroscience [105,109]. A number of international neuroscience projects have impressively expanded the computational and experimental borders. It is expected that in future, these projects will improve the applicability of modeling studies in neuroscience as well as their projection of highly complex biological reality of the human brain [112].

Acknowledgments

The authors thank Hossein Hassanpoor for his help in preparing the earlier version of the manuscript.

References

1. Nadkarni S, Jung P, Levine H. "Astrocytes optimize the synaptic transmission of information". PLOS Computational Biology. 2008; 4.
2. Myers E, Scharfman HE. "A role for hilar cells in pattern separation in the dentate gyrus: A computational approach". Hippocampus. 2009; 19: 321-337.
3. Wade JJ, McDaid LJ, Harkin J, Crunelli V, Kelso JA. "Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: A multiple modeling approach". PLoS One, vol. 6, no. 12, article e29445, 2011.
4. Li SC, Lindenberger U, Sikström S. "Aging cognition: From neuromodulation to representation". Trends in Cognitive Sciences. 2001; 5: 479-486.
5. Hewett T. "Teaching students to model neural circuits and neural networks using an electronic spreadsheet simulator". Behavior Research Methods, Instruments, & Computers. 1985; 17: 339-344.
6. Fred Wolf, Engelken R, Puelma-Touzel M, Weidinger JD, Neef A. "Dynamical models of cortical circuits". Current Opinion in Neurobiology. 2014; 25: 228-236.
7. Izhikevich EM. Which model to use for cortical spiking neurons? IEEE Transactions on Neural Networks. 2004; 15: 1063-1070.
8. Jolivet R, Kobayashi R, Rauch A, Naud R, Shinomoto S, Gerstner W. "A benchmark test for a quantitative assessment of simple neuron models". Journal of Neuroscience Methods. 2008; 169: 417-424.
9. Jolivet R, Roth A, Schurmann F, Gerstner W, Senn W. "Special issue on quantitative neuron modeling". Biological Cybernetics. 2008; 99: 237-239.
10. Jolivet R, Schurmann F, Berger TK, Naud R, Gerstner W, Roth A. "The quantitative single-neuron modeling competition". Biological Cybernetics. 2008; 99: 417-426.
11. Gerstner W, Naud R. Neuroscience. How good are neuron models? Science. 2009. 326: 379-380.
12. Huys QJ, Moutoussis M, Williams J. Are computational models of any use to psychiatry? Neural Networks. 2011; 24: 544-551.
13. Markram H. "Seven challenges for neuroscience". Functional Neurology. 2013; 28: 145-151.
14. Azevedo FA, Carvalho LR, Grinberg LT, et al. "Equal numbers of neuronal and non-neuronal cells make the human brain an isometrically scaled-up primate brain". Journal of Comparative Neurology. 2009; 513: 532-541.
15. Herculano-Houzel S. "The remarkable, yet not extraordinary, human brain as a scaled-up primate brain and its associated cost". Proc. Natl. Acad. Sci. USA. 2012; 109: 10661-10668.
16. Mattson MP. "Superior pattern processing is the essence of the evolved human brain". Frontiers in Neuroscience. 2014; 8: 265.
17. Drachman DA. Do we have brain to spare? Neurology. 2005; 64: 2004-2005.
18. Herculano-Houzel. "The human brain in numbers: A linearly scaled-up primate brain". Frontiers in Human Neuroscience. 2009; 3: 31.
19. Aimone JB, Gage FH. "Modeling new neuron function: A history of using computational neuroscience to study adult neurogenesis". European Journal of Neuroscience. 2011; 33:1160-1169.
20. Postnov DE, Ryazanova LS, Sosnovtseva OV. "Functional modeling of neural-glial interaction". Biosystems. 2007; 89: 84-91.
21. Porto-Pazos, Veiguela N, Mesejo P, et al. "Artificial astrocytes improve neural network performance". PLoS One. 2011; 6: e19109.
22. De Felipe J, Alonso-Nanclares L, Arellano JI. "Microstructure of the neocortex: Comparative aspects". Journal of Neurocytology. 2002; 31: 299-316.
23. Nedergaard M, Ransom B, Goldman SA. "New roles for astrocytes: Redefining the functional architecture of the brain". Trends in Neurosciences. 2003; 26: 523-530.
24. Sulston JE, Schierenberg E, White JG, Thomson JN. "The embryonic cell lineage of the nematode Caenorhabditis elegans". Developmental Biology. 1983; 100: 64-119.
25. Bass NH, Hess HH, Pope A, Thalheimer C. "Quantitative cytoarchitectonic distribution of neurons, glia, and DNa in rat cerebral cortex". Journal of Comparative Neurology. 1971; 143: 481-490.
26. Pakkenberg, Gundersen HJ. "Total number of neurons and glial cells in human brain nuclei estimated by the disector and the fractionator". Journal of Microscopy. 1988; 150: 1-20.
27. Pelvig P, Pakkenberg H, Stark AK, Pakkenberg B. "Neocortical glial cell numbers in human brains". Neurobiology of Aging. 2008; 29: 1754-1762.
28. Sherwood C, Stimpson CD, Raghanti MA, et al. "Evolution of increased glia-neuron ratios in the human frontal cortex". Proceedings of the National Academy of Sciences USA. 2006; 103: 13606-13611.
29. Grosche, Grosche J, Tackenberg M, et al. "Versatile and simple approach to determine astrocyte territories in mouse neocortex and hippocampus". PLoS One. 2013; 8: e69143.
30. Amenta, Bronzetti E, Sabbatini M, Vega JA. "Astrocyte changes in aging cerebral cortex and hippocampus: a quantitative immunohistochemical study". Microscopy Research and Technique. 1998; 43: 29-33.
31. Di Garbo. "Dynamics of a minimal neural model consisting of an astrocyte, a neuron, and an interneuron". Journal of Biological Physics. 2009; 35: 361-382.
32. Reato, Cammarota M, Parra LC, Carmignoto G. "Computational model of neuron-astrocyte interactions during focal seizure generation". Frontiers in Computational Neuroscience. 2012; 6.
33. Andersen BB, Korbo L, Pakkenberg B. "A quantitative study of the human cerebellum with unbiased stereological techniques". Journal of Comparative Neurology. 1992; 326: 549-560.
34. Megias M, Emri Z, Freund TF, Gulyas AI. "Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells". Neuroscience. 2001; 102: 527-540.
35. Spruston N. "Pyramidal neurons: Dendritic structure and synaptic integration". Nature Reviews Neuroscience. 2008; 9: 206-221.
36. Moser MB. Making more synapses: A way to store information? Cellular and Molecular Life Sciences. 1999; 55: 593-600.
37. Maguire, Gadian DG, Johnsrude IS, et al. "Navigation-related structural change in the hippocampi of taxi drivers". Proceedings of the National Academy of Sciences USA. 2000; 97: 4398-4403.
38. Acebes, Ferrus A. "Increasing the number of synapses modifies olfactory perception in Drosophila". The Journal of Neuroscience. 2001; 21: 6264-6273.
39. Majewska K, Newton JR, Sur M. "Remodeling of synaptic structure in sensory cortical areas in vivo". The Journal of Neuroscience. 2006; 26: 3021-3029.
40. Martin SJ, Grimwood PD, Morris RG. "Synaptic plasticity and memory: An evaluation of the hypothesis". Annual Review of Neuroscience. 2000; 23: 649-711.
41. Mayford M, Siegelbaum SA, Kandel ER. "Synapses and memory storage". Cold Spring Harbor Perspectives in Biology. 2012; 4: a005751.
42. Silberberg, Grillner S, LeBeau FE, Maex R, Markram H. "Synaptic pathways in neural microcircuits". Trends in Neurosciences. 2005; 28: 541-551.
43. Walikonis RS, Jensen ON, Mann M, Provance DW, Mercer JA Jr., Kennedy MB. "Identification of proteins in the postsynaptic density fraction by mass spectrometry". The Journal of Neuroscience. 2000; 20: 4069-4080;
44. De Bartolomeis, Latte G, Tomasetti C, Iasevoli F. "Glutamatergic postsynaptic density protein dysfunctions in synaptic plasticity and dendritic spines morphology: Relevance to schizophrenia and other behavioral disorders pathophysiology, and implications for novel therapeutic approaches". Molecular Neurobiology. 2014; 49: 484-511.
45. Pinto, Pagnamenta AT, Klei L, et al. "Functional impact of global rare copy number variation in autism spectrum disorders". Nature. 2010; 466: 368-372.
46. Bekkers JM. "Synaptic transmission: Functional autapses in the cortex". Current Biology. 2003; 13: 433-435,
47. Wang, Wang L, Chen Y. "Effect of autaptic activity on the response of a Hodgkin-Huxley neuron". Chaos. 2014; 24: 3.
48. Wang, Ma J, Chen Y, Chen Y. "Effect of an autapse on the firing pattern transition in a bursting neuron". Communications in Nonlinear Science and Numerical Simulation. 2014; 19: 3242-3254.
49. Leuner, Falduto J, Shors TJ. "Associative memory formation increases the observation of dendritic spines in the hippocampus". The Journal of Neuroscience. 2003; 23: 659-665.
50. McDonnell MD, Ward LM. "Small modifications to network topology can induce stochastic bistable spiking dynamics in a balanced cortical model". PLoS One. 2014; 9: 4.
51. Eguchi, Neymotin SA, Stringer SM. "Color opponent receptive fields self-organize in a biophysical model of visual cortex via spike-timing dependent plasticity." Frontiers in Neural Circuits. 2014; 8: 16,
52. Pyka M, Cheng S. "Pattern association and consolidation emerges from connectivity properties between cortex and hippocampus". PLoS One. 2014; 9: e85016.
53. Sinha, Ledbetter NM, Barbour DL. "Spike-timing computation properties of a feed-forward neural network model". Frontiers in Computational Neuroscience. 2014; 8: 5.
54. Abbott LF, Nelson SB. "Synaptic plasticity: taming the beast". Nature Neuroscience. 3: 1178-1183, 2000.
55. Lisman, Spruston N. "Questions about STDP as a General Model of Synaptic Plasticity". Frontiers in Synaptic Neuroscience. 2010; 2: 140.
56. Clopath, Gerstner W. "Voltage and Spike Timing Interact in STDP-A Unified Model". Frontiers in Synaptic Neuroscience. 2010; 2: 25.
57. Dutta Roy R, Stefan MI, Rosenmund C. "Biophysical properties of presynaptic short-term plasticity in hippocampal neurons: insights from electrophysiology, imaging and mechanistic models". Frontiers in Cellular Neuroscience. 2014; 8:141.
58. He Y, Kulasiri D, Samarasinghe S. "Systems biology of synaptic plasticity: A review on N-methyl-D-aspartate receptor mediated biochemical pathways and related mathematical models". Biosystems. 2014; 122: 7-18.
59. Purves, Augustine GJ, Fitzpatrick D, et al. Neuroscience, Sinauer Associates, Sunderland. 2012.
60. Watling. The Sigma-RBI Handbook of Receptor Classification and Signal Transduction, Sigma, Natick. 2001.
61. Bentivoglio M, Morelli M, Dunnett SB, Bentivoglio M, Björklund A, Hökfelt T, e tal. "Chapter-I The organization and circuits of mesencephalic dopaminergic neurons and the distribution of dopamine receptors in the brain". In Handbook of Chemical Neuroanatomy. Elsevier. 2005; 1-107.
62. Nichols E, Nichols CD. "Serotonin receptors". Chemical Reviews. 2008; 108: 1614-1641.
63. Bouwman M, Suffczynski P, Lopes da Silva FH, Maris E, van Rijn CM. "GABAergic mechanisms in absence epilepsy: A computational model of absence epilepsy simulating spike and wave discharges after vigabatrin in WAG/Rij rats," European Journal of Neuroscience. 2007; 25: 2783-2790.
64. Shevtsova NA, Manzke T, Molkov YI, et al. "Computational modeling of 5-HT receptor-mediated reorganization of the brainstem respiratory network". European Journal of Neuroscience. 2011; 34: 1276-1291.
65. Di Garbo, Barbi M, Chillemi S. The role of glutamatercic and GABAergic synapses on the dynamics of neural networks: How they impact the transition to seizure? Neurocomputing. 2013; 114: 15-23.
66. Stansberg, Vik-Mo AO, Holdhus R, et al. "Gene expression profiles in rat brain disclose CNS signature genes and regional patterns of functional specialisation". BMC Genomics. 2007; 8: 94.
67. Guilmatre, Huguet G, Delorme R, Bourgeron T. "The emerging role of SHANK genes in neuropsychiatric disorders". Developmental Neurobiology. 2014; 74: 113-122.
68. Henry M, Hohmann JG. "High-resolution gene expression atlases for adult and developing mouse brain and spinal cord". Mammalian Genome. 2012; 23: 539-549.
69. Shen H, Overly CC, Jones AR. "The Allen Human Brain Atlas: Comprehensive gene expression mapping of the human brain". Trends in Neurosciences. 2012; 35: 711-714.
70. Eberwine, Yeh H, Miyashiro K, et al. "Analysis of gene expression in single live neurons". Proceedings of the National Academy of Sciences USA. 1992; 89: 3010-3014.
71. Stahlberg, Andersson D, Aurelius J, et al. "Defining cell populations with single-cell gene expression profiling: Correlations and identification of astrocyte subpopulations". Nucleic Acids Research. 2011; 39: e24.
72. Kasabov N, Benuskova L. "Computational Neurogenetics". Journal of Computational and Theoretical Nanoscience. 2004; 1: 47-61.
73. Benuskova, Kasabov N. "Modeling brain dynamics using computational neurogenetic approach". Cognitive Neurodynamics. 2008; 2: 319-334.
74. Kasabov K, Schliebs R, Kojima H. "Probabilistic Computational Neurogenetic Modeling: From Cognitive Systems to Alzheimer's disease". IEEE Tran.sactions on Autonomous Mental Development. 2011; 3: 300-311.
75. Contreras-Vidal J. "Computer Modeling in Basal Ganglia Disorders". In Atypical Parkinsonian Disorders, Litvan I, Ed. 2005; 95-109.
76. Duch W. "Computational models of dementia and neurological problems". Methods in Molecular Biology. 2007; 401: 305-336.
77. Henning Proske, Jeanmonod D, Verschure PF. "A computational model of thalamocortical dysrhythmia". European Journal of Neuroscience. 2011; 33: 1281-1290.
78. Rubin, McIntyre CC, Turner RS, Wichmann T. "Basal ganglia activity patterns in parkinsonism and computational modeling of their downstream effects". European Journal of Neuroscience. 2012; 36: 2213-2228.
79. Montague PR, Dolan RJ, Friston KJ, Dayan P. "Computational psychiatry". Trends in Cognitive Sciences. 2012; 16: 72-80.
80. Izhikevich M. "Simple model of spiking neurons". IEEE Transactions on Neural Networks. 2003; 14: 1569-1572.
81. Prokin S, Kazantsev VB. "Analysis of pulsed-signal transmission in a system of interacting neural oscillators with frequency-dependent connections". Radiophysics and Quantum Electronics. 2012; 54: 763-772.
82. Yamazaki T, Tanaka S. "A spiking network model for passage-of-time representation in the cerebellum". European Journal of Neuroscience. 2007; 26: 2279-2292.
83. Edwards R, Gibson WG. "A model for Ca2+ waves in networks of glial cells incorporating both intercellular and extracellular communication pathways". Journal of Theoretical Biology. 2010; 263: 45-58.
84. Iacobas, Suadicani SO, Spray DC, Scemes E. "A stochastic two-dimensional model of intercellular Ca2+ wave spread in glia". Biophysical Journal. 2006; 90: 24-41.
85. Izhikevich M, Edelman GM. "Large-scale model of mammalian thalamocortical systems". Proceedings of the National Academy of Sciences USA. 2008; 105: 3593-3598.
86. Tang, Luo JM, Ma J. "Information transmission in a neuron-astrocyte coupled model". PLoS One. 2013; 8.
87. Garris PA, Ciolkowski EL, Pastore P, Wightman RM. "Efflux of dopamine from the synaptic cleft in the nucleus accumbens of the rat brain". The Journal of Neuroscience. 1994; 14: 6084-6093.
88. Kandel ER, Schwartz JH, Jessell TM. Principles of neural science. McGraw-Hill, New York. 2000.
89. Araque, Parpura V, Sanzgiri RP, Haydon PG. "Tripartite synapses: glia, the unacknowledged partner". Trends in Neurosciences. 1999; 22: 208-215.
90. Perea G, Navarrete M, Araque A. "Tripartite synapses: Astrocytes process and control synaptic information". Trends in Neurosciences. 2009; 32: 421-431.
91. Herz V, Gollisch T, Machens CK, Jaeger D. "Modeling single-neuron dynamics and computations: A balance of detail and abstraction". Science. 2006; 314: 80-85.
92. Tu JV. "Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes". Journal of Clinical Epidemiology. 1996; 49: 1225-1231.
93. Olden JD, Jackson DA. "Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks". Ecological Modelling. 2002; 154: 135-150.
94. Previdi. "Identification of black-box nonlinear models for lower limb movement control using functional electrical stimulation". Control Engineering Practice. 2002; 10: 91-99.
95. Lytton WW. "Computer modelling of epilepsy". Nature Reviews Neuroscience. 2008; 9: 626-637.
96. D'Angelo E, Solinas S, Garrido J, et al. "Realistic modeling of neurons and networks: Towards brain simulation". Functional Neurology. 2013; 28: 153-166.
97. Markram, Muller E, Ramaswamy S, et al. "Reconstruction and Simulation of Neocortical Microcircuitry". Cell. 2015; 163: 456-492.
98. Kai. "Rat brain-or a smidgeon of it -is modeled in a computer". 2015.
99. Eliasmith, Stewart TC, Choo X, et al. "A Large-Scale Model of the Functioning Brain". Science. 2012; 338: 1202-1205.
100. Wendling, Bartolomei F, Mina F, Huneau C, Benquet P. "Interictal spikes, fast ripples and seizures in partial epilepsies-combining multi-level computational models with experimental data". European Journal of Neuroscience. 2012; 36: 2164-2177.
101. Zandt J, Ten Haken B, van Putten MJ, Dahlem MA. "How does spreading depression spread? Physiology and modeling". Reviews in the Neurosciences. 2015; 26: 183-198.
102. Corradi, Porro I, Schenone A, et al. "A repository based on a dynamically extensible data model supporting multidisciplinary research in neuroscience". BMC Medical Informatics and Decision Making. 2012; 12: 115.
103. Stefanescu RA, Shivakeshavan RG, Talathi SS. "Computational models of epilepsy". Seizure. 2012; 21: 748-759.
104. Huang T, Chen L, Zheng M. "Integrated analysis of multiscale large-scale biological data for investigating human disease". BioMed Research International. 2015.
105. Wendling. "Computational models of epileptic activity: A bridge between observation and pathophysiological interpretation". Expert Review of Neurotherapeutics. 2008; 8: 889-896.
106. Goldman S, Golowasch J, Marder E, Abbott LF. "Global structure, robustness, and modulation of neuronal models". The Journal of Neuroscience. 2001; 21: 5229-5238.
107. Erik De Schutter. "Using realistic models to study synaptic integration in cerebellar Purkinje cells". Reviews in the Neurosciences. 1999; 10: 233-245.
108. Jorgenson LA, Newsome WT, Anderson DJ, et al. "The BRAIN Initiative: Developing technology to catalyse neuroscience discovery". Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2015; 370.
109. Kotter R. "Trends in European computational neuroscience". Reviews in the Neurosciences. 1999; 10: 175-179.
110. Duch W, Dobosz K, Mikolajewski D. Autism and ADHD-Two Ends of the Same Spectrum? In Neural Information Processing, Lee M, Hirose A, Hou ZG, Kil R, et al. Springer Berlin Heidelberg. 2013; 623-630.
111. Postnova S, Finke C, Huber M, Voigt K, Braun H. "Conductance-Based Models for the Evaluation of Brain Functions, Disorders, and Drug Effects". In Biosimulation in Biomedical Research, Health Care and Drug Development, Mosekilde E, Sosnovtseva O, Rostami-Hodjegan A. Springer Vienna. 2012; 97-132.
112. Huang ZJ, Luo L. "NEUROSCIENCE. It takes the world to understand the brain". Science. 2015: 350: 42-44.
113. Krioukov. "Brain theory". Frontiers in Computational Neuroscience. 2014; 8.
114. Volman V, Bazhenov M, Sejnowski TJ. "Computational models of neuron-astrocyte interaction in epilepsy". Frontiers in Computational Neuroscience. 2012; 6.

Download PDF

Citation: Mohamad ASK and Reza M. Computational Models in Neuroscience: How real are they? A Critical Review of Status and Suggestions. Austin Neurol & Neurosci. 2016; 1(2): 1008.

Home

Journal Scope

Online First

Current Issue

Editorial Board

Instruction for Authors

Submit Your Article

Contact Us