Janus Emulsions of Bertholletia Excelsa Oil and Silicone Oil

Special Article - Micro Fluidics

Austin J Anal Pharm Chem. 2015;2(3): 1041.

Janus Emulsions of Bertholletia Excelsa Oil and Silicone Oil

Leonardi GR1,2, Silva MM¹, Monteiro e Silva SA², Perrechil FA¹ and Friberg SE³*

1Institute for Environmental, Chemical and Pharmaceutical Sciences, Federal University of São Paulo, UNIFESP, Diadema, Brazil

2Medicine Department - Federal University of São Paulo – UNIFESP, São Paulo, Brazil

3Ugelstad Laboratory, NTNU, Norway

*Corresponding author: Friberg SE, Ugelstad Laboratory, USA.

Received: April 12, 2015; Accepted: May 04, 2015; Published: May 05, 2015

Abstract

Janus emulsions of Bertholletia Excelsa oil and silicone oil in water were prepared in batch by high energy emulsification and their destabilization studied by observing the creaming and final separation of the two oils. The creaming was shown to be characteristic of a flocculated emulsion in accordance with the optical microscope image of a concentrated emulsion, but with few drop-drop contacts. During the creaming process the Janus drops suffered coalescence, but retained the Janus topology till the final stage after more than a month of storage, at which time the two oils set off separation into two bulk liquids. The unexpected stability of the topology per se indicated a more general importance of Janus emulsions than hitherto recognized and prompted a calculation to compare the relative free energy reduction during the coalescence versus the increase during the separation of the two oils. The latter energy change was significantly superior and was concluded to be an essential factor for the stability of the Janus topology.

Keywords: Emulsions; Janus topology; Coalescence free energy; Interfacial free energy; Cerberus emulsions

Introduction

Among the many emulsion varieties [1], multiple emulsions [2, 3] early found wide spread applications [4] within foods [5], drugs and cosmetics [6]. One reason for the interest in double emulsions rests with the potential to combine beneficial properties of different oils, e.g. improving the feel of cosmetics by adding silicon oil to vegetable oil formulations [7,8]. Amongst other benefits may be mentioned taking advantage of the separate compartment structure by isolating mutually sensitive compounds or reducing the dissolution rate of specific compounds [9]. The formulation of double emulsions was for a long time focusing on solving the stability problems [3,10,11]: a focus that was meaningfully altered with the introduction of the microfluidics method [12] with its subsequent novel applications [13,14].

In the microfluidics process Janus emulsions and more complex formulations were prepared [15,16] under conditions close to equilibrium. As a consequence, the correlation between the drop topology and the interfacial thermodynamics at the contact line became of interest with several comprehensive investigations [17,18,19,20]. With the fundamentals clarified as well as a large number of advanced applications introduced, the framework for the field appeared defined and the future development predictable, taking into consideration the limitation to small volumes of the microfluidics method.

However, recent publications [21,22,23] appear to substantially enlarge the field of Janus emulsion applications. It was shown that well defined Janus emulsions could also be prepared in a batch process, allowing Janus emulsion applications also into the commodities area [24]. The discovery prompted extended thermodynamic investigations into Janus emulsion topology, revealing a selective inversion of a Janus drop to change the Janus emulsion of a vegetable oil/silicone (VO/SO) oil in an aqueous solution from the original (SO + VO)/W to an (SO + W)/VO configuration [25,26,27].

With these recent developments, the potential appears realistic for an extension of the Janus emulsion concept also into personal care and pharmaceutical formulations and with this contribution the authors introduce a Janus emulsion of silicone oil (SO) with a Brazilian vegetable oil from Bertholletia Excelsa. This oil has, as many other vegetable oils from Brazil, a number of beneficial properties [28,29,30] and the authors felt the need for an introductory investigation into the fundamentals of preparing Janus emulsions from a selected Brazilian vegetable oil combined with a silicone. The results indicate a more wide spread importance of Janus emulsions and with this contribution we introduce the basic conditions for such an emulsion, built on a silicone oil and the vegetable oil from Bertholletia Excelsa.

Experimental Materials

The materials used to prepare the systems were polydimethylsiloxane polymer, 100 centistokes (silicone fluid Xiameter® PMX-200), SO, kindly donated by Dow Corning (USA), Bertholletia Excelsa oil, VO, kindly donated by MAPRIC (Brazil), polyoxyethylene sorbitan monooleate (Tween 80) acquired from Synth (Brazil), and distilled water.

Janus emulsion preparation

Janus emulsions were prepared by first mixing vegetable oil (VO) and, silicone oil (SO). To this mixture was gradually added an aqueous phase with Tween 80 (Aq) to form the final composition in weight fractions, VO 0.08, SO 0.32, Tween 80 0.06 and water 0.54. The emulsions were mixed for 5 min on Vortex Mixer AP 56 (Phoenix Luferco, Brazil). The test tubes were sealed with a plastic cap to avoid water evaporation.

Microscopy

Aliquots of each sample were removed for microscopy observation and photographs were recorded until 40 days. A small sample of each emulsion placed on a microscopy slide, Bioslide, 26 × 76 mm, one set under a cover glass, 18 × 18 mm and a second group observed without cover in an optical microscope model Primo Star (Zeiss, Germany) with a yellow coded objective EPIPLAN 10×/0.2.

Results

The outcome of the experiments on the emulsions of a composition according the section 2.2, will be presented in the following order. The first section follows the creaming of the emulsions by photos of the emulsion test tubes versus time and, secondly, optical microscopy images are shown of the emulsions. The optical microscopy images offer direct information about the essential aspect of the Janus emulsions, the topology of the drops. However, the value of such material is limited without knowledge about the emulsion “stability”, i.e. the rate of creaming and flocculation/ coalescence and a qualitative account of the creaming process will first be given, Figure 1.

Figure 1: Photos of the emulsion test tubes after different times at rest.

    

    
    

    

    Figure 1:  Photos of the emulsion test tubes after different times at rest.

Emulsion creaming

The destabilization route of emulsions includes two main and partially dependent processes; drop/drop interactions in the form of flocculation/coalescence and, in parallel, creaming/sedimentation. In addition, Ostwald ripening plays a role for emulsions with significant stability [9]. Figure 1 presents a macroscopic view of the emulsion destabilization.

The results in Figure 1 illustrate one factor in the destabilization process of the emulsion; the creaming, while the additional processes require further information. However, even this partial material enables some essential knowledge about a Janus emulsion to be attained and a reflection on essential earlier contributions is useful. The creaming of traditional single-oil emulsion creaming was early comprehensively investigated by Dickinson et al [31] as well as by Chanami and McClements [32]. The results in the latter publication are of special interest for the present contribution, because of the difference in the creaming profiles between non-flocculated and flocculated emulsions. In the former, the backscattering develops into a gradual increase of the scattering intensity with the height of the emulsion layer, while for the latter emulsions, the profile is square with a defined transition point from depleted to increased scattering. The present results show a definite pattern of the latter, i.e. the emulsion is gradually and evenly depleted of drops to a certain height of the emulsion. The final layer dimensions in Figure 1 were used to estimate the volume fraction of the oil drops in the upper layer of the figure assuming the lower layer to consist of the aqueous solution only. It gave a final volume fraction of dispersed phase approximately equal to 0.74, equivalent to a weight fraction of 0.73, taking the lower density of the oils in consideration [29]. An emulsion with this large fraction of oil is with necessity is highly crowded and the microscopy images in the following section will provide information about the packing of the oil drops as well as of their topology.

Optical microscopy

As indicated by the estimated oil volume fraction in the earlier section the emulsion layer, Figure 1, shows a highly crowded dispersion, Figure 2A. The image also confirms an earlier finding that optical microscopy of Janus emulsion drop is strongly dependent on the effect of the cover glass on the sample [33]. The close packed irregular pattern observed in the sample with no cover glass, Figure 2A, is changed to an image of mostly well-defined Janus drops, but with varied oil volume ratio, after the application of a cover glass.

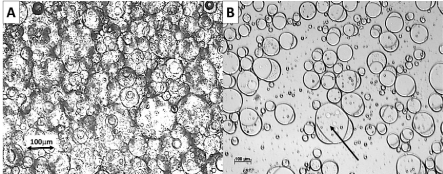
Figure 2: Optical microscopy images of the emulsion. Composition in weight fractions: Bertholletia Excelsa oil 0.08, Silicone oil 0.32, Tween 80 0.06 and water 0.54. A: no cover glass; B: cover glass

    

    
    

    

    Figure 2:  Optical microscopy images of the emulsion. Composition in weight
fractions: Bertholletia Excelsa oil 0.08, Silicone oil 0.32, Tween 80 0.06 and
water 0.54.
A: no cover glass; B: cover glass

The sample with no cover glass shows a broad spectrum of close packed combination drops with different sizes, Figure 2A. In fact, each drop is in contact with a large number of adjacent drops, but without visible mutual distortion from the spherical shape. The overall pattern is one of a number of large (diameter ≈ 100μm) of SO drops surrounded by a larger number of smaller (diameter 10 - 30μm) VO drops in an irregular arrangement; certainly not of well-defined Janus drops. This set of circumstances is radically changed after the sample has been sheared during the application of the cover glass [33]. The volume fraction of dispersed phase from Figure 1 equals 0.74, and it would be tempting to identify it as due to hexagonal close packing of equally sized solid spheres with a volume fraction of dispersed particles of π/3√2 [34], but this number is for equally sized spheres. The close packing of spheres of different size shows significantly greater values [35], as is the case for a packing with less a number of adjacent spheres in contact, when the void fraction may increase to as high as 0.9445 [34]. Hence, the value of a packing fraction of 0.74 per se, the densest packing of non-frictional solid spheres, cannot be used for the final interpretation of the condition of the present emulsion, while the present results are for a top layer in an emulsion after creaming.

The image after applying a cover glass, Figure 2B, shows Janus drops with varied volume fraction of VO, but all with similar angles at the contact line. It is essential to realize that the projection of the drop provides information about the angles at the contact line first after recalculation [36]. It would be of interest to use Figure 2B to measure the angles β and δ, Figure 3. However, the focus of the contribution is the time dependent behavior of the emulsions and the angles will be analyzed first under the Discussion section. The remaining part of the narrative, instead, will first and foremost focus on the essential problem at hand; the time dependent behavior of the samples; the creaming process.

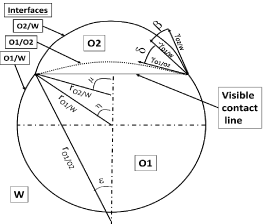
Figure 3: The angles and dimensions of a Janus drop.

    

    
    

    

    Figure 3:  The angles and dimensions of a Janus drop.

A qualitative evaluation of the process is possible after a comparison of the information from the images in Figures 1 and 2A. The emulsion, immediately after preparation, forms a flocculated system of multi-disperse drops with a low number of contact points to adjacent drops, Figure 2A. Such a poly-disperse system allows diffusion of creaming drops [31, 32] until a critical volume fraction of drops is reached [37], when the diffusion coefficient reaches zero. The recent publication [37] shows that number in the range 0.57- 0.61; a credible number for the emulsion drop packing after short creaming times, Figure 1. Hence, the square shape of the turbidity versus emulsion height in Figure 1 is plausibly explained by assuming the initial creaming of the emulsion to cause an arrest of the mobility of the drops. The initial volume fraction is significantly lower than 0.74, but higher than 0.41. In the beginning, the layer is still rather open and would allow the inclusion of the smaller drops left in the aqueous layer. This interpretation is certainly tentative and additional information will be obtained from the microscope images of samples after storage, Figure 4. For comparison, the images are from samples with cover glass and without.

Figure 4: Microscopy photos of the emulsion layer after different times at rest. A: No cover glass; B: Cover glass

    

    
    

    

    Figure 4:  Microscopy photos of the emulsion layer after different times at
rest.
A: No cover glass; B: Cover glass

The general trend of the images from covered and uncovered samples do agree. The image after storage for one hour shows a more close packed arrangement including more drops of smaller size than for the freshly prepared emulsion. After prolonged storage for 40 days there are an increased number of large drops. Both these feature lend measured support of the earlier tentative conclusion with the following summation of three successive processes at work. The initial creaming predominantly moves large drops towards the upper layer, because of the strong dependence on the drop radius of the creaming rate [31,32]. At a certain concentration of drops in the emulsion layer they become virtually immobilized [37] into a random close packing at a comparatively low volume fraction; still significantly far from the ultimate close packing. This arrangement of large drops, 0hr, Figure 4, admits smaller drops to penetrate into the voids of the layer, 1hr, Figure 4 in the second stage of the process. Prolonged storage changes the dynamics into the third stage. Now, the destabilization by coalescence becomes more significant and larger drops are found.

Additionally, Figure 4 leaves information, which carries substantial weight for the main theme of the investigation. The microscopy images for 40 days storage show a reduced number of small drops, due to coalescence. However, among the newly formed drops virtually all have the Janus topology, i.e. there is effectively no separation of the two oils into separate drops. Tentatively, the interfacial free energy is of a magnitude to retain the Janus topology and the interfacial free energies for relevant topologies will be analyzed in the Discussion section.

Discussion

The specific information gained from the experiments will be analyzed, but, prior to any such examination, it is truly essential to emphasize the fact that the Janus emulsions per se indicate a solution to the long and ardent efforts to stabilize dual emulsions using the classical approach [3,10,11]. The Janus emulsions offer a simpler solution to this essential problem and a rapid development is anticipated within the area in question. The present contribution offers specific information about the creaming process in a concentrated Janus emulsion with limited stability against this process. The results from the creaming process, Figures 1 and 4, offer useful material to evaluate the mechanism of final coalescence, whose interpretation cogently leads to the second aspect, which is concerned with the crucial intrinsic stability of the Janus topology per se. The first attribute, the creaming process as such, has been given a primary evaluation under the Results section and will not be further assessed. However, the second characteristic, the potential effect of the Janus topology interfacial free energy on the flocculation/coalescence destabilization process deserves an examination as to its fundamentals. The central factor for this analysis is the interfacial free energy difference between two mechanisms in the coalescence process. Two Janus drops may either coalesce to a single Janus drop, or the coalescence may result in two or more separate single drops of Bertholletia Excelsa and silicone oil. The first indication of the mechanism is offered by the microscopy photos at later stages in the process, Figure 4. Virtually, no drops of a single oil were found in the images or during the direct visual observation of the sample in the microscope and an equitable conclusion would be that the difference in interfacial energy between the two scenarios is sufficient to prevent the oils in the Janus drop to form separate drops. Such a conclusion would be confirmed or questioned depended on free energy calculations, based on the numbers for the interfacial tensions. Unfortunately, for the present emulsions, the numbers for the interfacial tensions at the actual surfactant concentration could not obtained at a consistent accuracy to be sufficient for a precise analysis. Instead, a graphic evaluation of a typical optical microscopy photo, Figure 4A, is introduced as a means to attain the necessary information.

The method is both simple and rapid, Figure 5, and can be made by someone with no special skills that would require a period of training. Nonetheless, a necessary qualification is to draw attention to the mandatory condition for the correct interpretation of the geometry; a straight contact line in the photo, Figure 5A. Conversely, the correction of the drop profile [36] is truly miniscule in the present case; of the order 10-6, and the picture was used for the subsequent analysis.

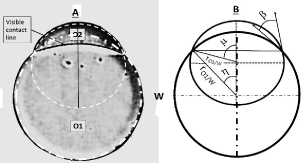
Figure 5: The model system used for calculating the energy difference during coalescence (See text) A. Micro-photo of a Janus drop from the emulsion, B. Drawing with features, directly available from image A.

    

    
    

    

    Figure 5:  The model system used for calculating the energy difference during
coalescence (See text)
A. Micro-photo of a Janus drop from the emulsion,
B. Drawing with features, directly available from image A.

The photo in Figure 5A, was supplemented by projections in dashed white lines of the complete spheres of O1 and O2, in order to extract available information from the photo with equitable accuracy. The following information was found of dimensions and angles; β = 25°, η = 40.9°, μ= η + β = 65.93°[26] and rO2/W = sinη/sinμ = 0.7175. The assumption of rO1/W =1 and γO1/W = 1 was made to make the numbers dimensionless. The numbers are utilized to calculate the all-inclusive drop topology from the different equilibria, based on the equilibrium at the contact line

1 = (γO2/W)cosβ + (γO1/O2)cosδ

(γO2/W)sinβ= (γO1/O2 )sinδ [2]

Pressure equilibrium at O1/W and O2/W interfaces from the pressure difference over a spherical interface; ΔP = 2γ/r

1 = γO1/O2/rO1/O2 + γO2/W/rO2/W [3]

The number of equations is not sufficient to solve for all the remaining variables and a numerical approach was, instead, chosen. In its primary step tanδ versus γO2/W was established from the equilibrium at the contact line.

tanδ = (γO2/W)sinβ/(1 - (γO2/W)cosβ) =

0.4226γO2/W/(1 - 0.9063 γO2/W) [4]

from which δ versus γO2/W is obtained. Subsequently, the trigonometric functions of δ were employed to calculate γO1/O2 andrO1/ O2 versus γO2/W. (The numbers are available from the senior author at stic30kan@gmail.com)

Finally, γO2/W was plotted against the pressure difference over the interfaces O1/O2, ΔP, Figure 6.

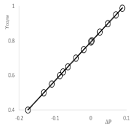
Figure 6: The pressure difference, P, over the interface O1/O2 versus the γO2/W

    

    
    

    

    Figure 6:  The pressure difference, P, over the interface O1/O2 versus the
γO2/W.

The empirical equation for the line is

γO2/W = 2.2375ΔP + 0.794 (R² = 1) [5]

i.e. the γO2/W = 0.794 for the emulsion drop in Figure 5.

Remaining essentials were computed; δ = 53. 0°, γO1/O2 = 0.420, rO1/ O2 = -3.125 and ε = η - δ = -12.1°, i.e. the pressures are virtually equal in the O1 and O2 caps, within the accuracy of the basic numbers.

The information about the topology of the Janus drop is now sufficient (with the necessary qualification of uncertain accuracy) for an evaluation of the relative importance of the interfacial energies for the retained Janus topology during coalescence. The relevant energies involved in the comparison are the energy gain during coalescence of two Janus drops, forming either a larger Janus drop or two separate spherical drops of O1 and O2. The alternative; forming a multiple of separate drops, is obviously less favorable and is not considered.

The surface free energies to be compared are the following. Two Janus drops of the dimensions of the model system coalesce, and a length scale increase of 21/3 and an increase of the areas by 22/3 is assumed. The Janus drop (rO1/W = 1) area of a sphere cap equals 2πrh with hO1/W = 1 + cosη, hO2/W = rO2/W(1 - cosμ) and hO1/O2 = -rO1/O2(1 - cosε) and the reduction of free energy for the coalescence of two drops to a single one equals 19.4. The volume of a cap VC = 4πh²(3r – h)/3 and free interfacial energy of the separated drops equals (4π)1/332/3(VO1 2/3 + VO2 2/3). The interfacial free energy of the single Janus drop is less than that of two separate drops by 28.4, a number significantly in excess of the energy gain during the coalescence (Numbers available from the senior author at stic30kan@gmail.com).

The numbers, although only from one selected example, manifestly demonstrate the weight of the interfacial free energy of the Janus drop for the long term stability of such emulsions.

The conclusions from the results of the model drop calculations can now be reflected against the observations of the images on the microscope photographs, Figure 4, which shows no presence of single-oil drops. Furthermore, even if such images were visible, it is necessary to attain, which of these images is exposing only the cap of one oil to the observer, due to specific orientation of the Janus drops. The probability of such an occurrence may be estimated as proportional to the fraction to which half the combined sphere contains any part of the cap in question. An exact calculation of this probability depends on both rO1/W as wells rO2/W and will not be performed. For the present case, assume the two radii as equal and the probability depends only on the distance of the visible contact line from the top of the sphere, h, giving a probability of P = h/r. In the model drop, Figure 5, h = 0.24 and the virtual absence of singleoil drops strongly supports a conclusion that the emulsion drops in the last stages retain the Janus topology. The remarkable intrinsic stability of the Janus topology is an interesting feature and its more general importance will be investigated in future general research.

Conclusions

  • Janus emulsions were prepared from a Brazilian vegetable oil of the Bertholletia Excelsa nut combined with silicone oil.
  • The microscopy image of the Janus drops was used to calculate the interfacial thermodynamics of the drops.
  • The experimental results showed the interfacial free energy of the drop to of a magnitude have a significant effect on the emulsion coalescence process.
  • The results confirmed that the earlier stability problems with dual oil emulsions may be substantially alleviated by formulation using Janus drops.

Acknowledgments

The authors wish to thank CNPq(Conselho Nacional de Desenvolvimento Científico e Tecnológico) for financial support. The senior author is grateful to the Ugelstad Laboratory, Trondheim, NO for support.

References

  1. J Sjoblom. (Ed.). Emulsion and Emulsion Stability, 2nd Ed., CRC Press LLC, Boca Raton, FL, 2006.
  2. TF Tadros. Colloids aspects of cosmetic formulations with particular reference to polymeric surfactants, in T F Tadros (Ed). Colloids in Cosmetics and Personal Care, Viley-Vch Verlag Wernheim DE. 2008; 1 – 34.
  3. A Aserin. Multiple emulsions: technology and applications: John Wiley & Sons New Jersey (2008).
  4. S Mataumoto, W. Kang. Formation and applications of multiple emulsions. J. Dispersion Sci. Technol. 1989; 10: 455-482.
  5. E Dickinson. Double Emulsions Stabilized by Food Biopolymers. Food Biophysics. 2011; 6: 1-11.
  6. ME Carlotti, M. Gallarate, S. Sapino, E. Ugazio, S. Morel. W/O/W multiple emulsions for dermatological and cosmetic use, obtained with ethylene oxide free emulsifiers. J. Dispersion Sci. Technol. 2005; 26: 183-192.
  7. A-L Girboux, E. Courbon. Enhancing the feel of vegetable oils with silicone. Cosmet. Toiletries. 2008; 49-50, 52-54, 56.
  8. T O'Lenick, T O'Lenick. Altering organic oils with silicones. Household Pers. Care Today. 2011; 72-75.
  9. F Leal-Calderon, V Schmitt, J Bibette. Emulsion science: basic principles. Springer. 2007; 173-199.
  10. Kanouni M, Rosano HL, Naouli N. Preparation of a stable double emulsion (W1/O/W2): role of the interfacial films on the stability of the system. Adv Colloid Interface Sci. 2002; 99: 229-254.
  11. JS Sander, AR Studart, L Isa, PA Rühs, P Fischer. Stabilization mechanism of double emulsions made by microfluidics. Soft Matter. 2012; 8: 11471-11477.
  12. T Nisisako, S Okushima, T. Torii. Controlled formulation of monodisperse double emulsions in a multiple- phase microfluidic system. Soft Matter. 2005; 1: 23-27.
  13. Wang JT, Wang J, Han JJ. Fabrication of advanced particles and particle-based materials assisted by droplet-based microfluidics. Small. 2011; 7: 1728-1754.
  14. AR Abate, DA Weitz, C-H Chen, EM Terentjev, D Lee. Microfluidic assembly of magnetic hydrogel particles with uniformly anisotropic structure. Adv. Mater. 2009; 21: 3201-3204.
  15. RK Shah et al. Designer emulsions using microfluidics. Materials Today. 2008; 11: 18-27.
  16. Chu LY, Utada AS, Shah RK, Kim JW, Weitz DA. Controllable monodisperse multiple emulsions. Angew Chem Int Ed Engl. 2007; 46: 8970-8974.
  17. Pannacci N, Bruus H, Bartolo D, Etchart I, Lockhart T, Hennequin Y, et al. Equilibrium and nonequilibrium states in microfluidic double emulsions. Phys Rev Lett. 2008; 101: 164502.
  18. J Guzowski, PM Korczyk, S Jakiela, P Garstecki. The structure and stability of multiple micro- droplets. Soft Matter. 2012; 8: 7269-7278.
  19. MJ Neeson, DYC Chan, RF Tabor, F Grieser, RR Dagastine. Compound sessile drops. Soft Matter. 2012; 8: 11042-11050.
  20. Asai M, Cacciuto A, Kumar SK. Quantitative analogy between polymer-grafted nanoparticles and patchy particles. Soft Matter. 2015; 11: 793-797.
  21. Hasinovic H, Friberg SE, Rong G. A one-step process to a Janus emulsion. J Colloid Interface Sci. 2011; 354: 424-426.
  22. Hasinovic H, Friberg SE. One-step inversion process to a Janus emulsion with two mutually insoluble oils. Langmuir. 2011; 27: 6584-6588.
  23. Ge L, Shao W, Lu S, Guo R. Droplet topology control of Janus emulsion prepared in one-step high energy mixing. Soft Matter. 2014; 10: 4498-4505.
  24. Ge L, Lu S, Guo R. Janus emulsions formed with a polymerizable monomer, silicone oil, and Tween 80 aqueous solution. J Colloid Interface Sci. 2014; 423: 108-112.
  25. Friberg SE, Kovach I, Koetz J. Equilibrium topology and partial inversion of Janus drops: a numerical analysis. Chemphyschem. 2013; 14: 3772-3776.
  26. Friberg SE. Selective emulsion inversion in an equilibrium Janus drop. 1. Unlimited space. J Colloid Interface Sci. 2014; 416: 167-171.
  27. GR Leonardi, FA Perrechil, LP Silveira, HO Brunca, SE Friberg. Silicone/vegetable oil Janus emulsion. Topological stability versus interfacial tensions and relative oil volumes. J. Colloid Interface Sci., Ahead of Print. 2014.
  28. M Athar, SM Nasir. Taxonomic perspective of plant species yielding vegetable oils used in cosmetics and skin care products. Afr. J. Biotechnol. 2005; 4: 36-44.
  29. VQ Neto et al. Brazil nut (Bertholletiaexcelsa HBK) seed kernel oil: Characterization and thermal stability. Rev. Biol. Farm. 2009; 3: 33-42.
  30. M Martins, AM Klusczcovski, VM Scussel. In vitro activity of the Brazil nut (Bertholletiaexcelsa H.B.K.) oil in aflatoxigenic strains of Aspergillusparasiticus. Eur. Food Res. Technol. 2014; 239: 687-693.
  31. Dickinson E, Golding M, Povey MJW. Creaming and Flocculation of Oil-in-Water Emulsions Containing Sodium Caseinate J Colloid Interface Sci. 1997; 185: 515-529.
  32. Chanamai R, McClements DJ. Creaming Stability of Flocculated Monodisperse Oil-in-Water Emulsions. J Colloid Interface Sci. 2000; 225: 214-218.
  33. H. Hasinovic, C. Boggs, S.E. Friberg, I. Kovach, J. Koetz. Janus Emulsions from a One-Step Process; Optical Microscopy Images. J. Dispersion Sci. Technol. 2014; 35: 613-618.
  34. M. Gardner, "Packing Spheres." Ch. 10. In: The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, W. W. Norton, New York, 2001, 128-136.
  35. Desmond KW, Weeks ER. Influence of particle size distribution on random close packing of spheres. Phys Rev E Stat Nonlin Soft Matter Phys. 2014; 90: 022204.
  36. FA Perechil, GR Leonardi, SE Friberg. Optical microscopy and surface thermodynamics of Janus emulsions, In: Microscopy Advances in scientific research and education Vol. 2 A. Mendez-Vila, ed. Formatex, Bayadoz, SP. 2014; 1036-1042.
  37. Zaccarelli E, Liddle SM, Poon WC. On polydispersity and the hard sphere glass transition. Soft Matter. 2015; 11: 324-330.

Citation: Leonardi GR, Silva MM, Monteiro e Silva SA, Perrechil FA and Friberg SE. Janus Emulsions of Bertholletia Excelsa Oil and Silicone Oil. Austin J Anal Pharm Chem. 2015;2(3): 1041. ISSN:2381-8913