A Route Map Proposal as the Topological Equivalent of the Ladder Design (65000 Years Ago) at La Pasiega Cave

Special Article - Civilization

Austin Anthropol. 2019; 3(2): 1011.

A Route Map Proposal as the Topological Equivalent of the Ladder Design (65000 Years Ago) at La Pasiega Cave

J. C. Flores*

Facultad de Ciencias, Universidad de Tarapacá, Casilla 7-D, Arica-Chile

*Corresponding author: Flores JC, Facultad de Ciencias, Universidad de Tarapacá, Casilla 7-D, Arica- Chile

Received: November 28, 2019; Accepted: December 17, 2019; Published: December 24, 2019

Abstract

The ladder design in the La Pasiega cave (Spain) possesses geometrical, entropic and mathematical properties of practical relevance. The approximate 5:3:9 ratio of its enclosed spaces seems correlated with walking areas within the cave. The schema’s compositional strokes are directionally inclined mainly at angles of 0o and 90o with a proportion of 7% and 20% respectively. Moreover, the prolific strokes within that defined interval suggest that the author was right-handed. The ladder five-node schema with three enclosed areas seems topologically equivalent to a virtual route map inside the cave. This conceivable scheme, created perhaps 65,000 years ago, still can yield valuable topographical information on paths inside the cave. Additionally, the full panel contains other designs or figures related to other epochs, nevertheless, the ladder entropyinformation is smaller than the rest, and consequently, it is more precise.

Keywords: Design in a cave; Topographic information; Archaeology; Topologic equivalences

Introduction

The Cave of La Pasiega, located in Cantabria, Spain, contains a ladder-shaped design among other draws (Panel 78, Hall XI, Gallery C; see Figure 1) and recently attributed to Neanderthals with a date of origin that preceded the advent of modern humans (Homo sapiens) by at least 20,000 years in the region [1]. Nevertheless, at the moment, it remains a controversial topic [2,3]. Debates on Neanderthals “complex” symbolic capacities have been intense [4,5,6], however, the hypothetical subject of this paper only focuses on the possible topographical abilities of the author of the ladder. Namely, I modestly conjecture a conceptual topographic ability of the author of the mentioned design.

Figure 1: Henri Breuil’s drawing (1913) of Panel 78 in the La Pasiega cave in Cantabria, Spain. The original “ladder” design found in the cave was apparently painted before the advent of modern humans. Actual photographs of the design can be found in the Web. The ladder encloses three spaces (top, middle and bottom) in an approximate ratio of 5:3:9. This study considers the statistical, geometrical and informational aspect only of the ladder. In general, figures have different dates; nevertheless, the ladder seems more ancient.

    

    
    

    

    Figure 1: Henri Breuil’s drawing (1913) of Panel 78 in the La Pasiega cave
in Cantabria, Spain. The original “ladder” design found in the cave was
apparently painted before the advent of modern humans. Actual photographs
of the design can be found in the Web. The ladder encloses three spaces (top,
middle and bottom) in an approximate ratio of 5:3:9. This study considers the
statistical, geometrical and informational aspect only of the ladder. In general,
figures have different dates; nevertheless, the ladder seems more ancient.

Additionally, a longstanding debate has centered on the question of whether or not Neanderthals and Modern Humans are different species. Moreover, there is considerable controversy regarding the factors that led to the disappearance of Neanderthals [7-12]. However, these debates are not appropriate to this discussion. As mentioned before, the focal topic here is only the potential significance of the ladder design. An underlying assumption in this work is that Breuil’s drawing, shown in Figure 1, is an accurate representation of the original panel, containing the ladder-shaped, found in the mentioned cave.

Related to the rest of the panel, the animal figures in the board were added years after the ladder was inscribed. The series of dots with relative area-variance of 44% have, to the best of my knowledge, an unclear sense (approximately 150, distributed within three respective groups comprising 17, 46, and 87 dots). The lower “triangle” or inverted “tunnel entrance” likewise possesses an unclear significance to me.

Ladder’s Geometrical Properties

The ladder design has measurable geometric and mathematic properties. For instance, the ratio of the three enclosed areas, extending from the up to the bottom portion, is approximately 5:3:9.

Moreover, as the twenty bars histogram depicted in Figure 2(a) shows, the main directionalities of the “brushstrokes” are at 0o and 90o angles (Image-J software) with a percentage of 7% and almost 20% respectively.

Figure 2: (a) Amount f of stroke directionalities on the ladder. Directionalities mainly are between 0o and 90o angles (red frame). The inset graphic (b) corresponds to the directionalities of the entire panel (Figure 1) showing that there are less privileged directions than the ladder or, equivalently, the full panel has major entropy (i.e., the ladder has more precise information). (b) Shows a histogram with the directionalities of the full panel. It is smoother than the ladder because there are more curved designs. As mentioned, the maximal strokes in the ladder (Figure 2(a)) are at 90o corresponding almost to 20% of the total, whereas in the entire panel (Figure 2(b)), the maximal strokes also at 90o reach only 6%. Consequently, the ladder contains more specific directions than the full panel.

    

    
    

    

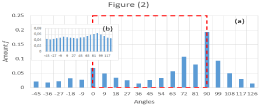
    Figure 2: (a) Amount f of stroke directionalities on the ladder. Directionalities
mainly are between 0o and 90o angles (red frame). The inset graphic (b)
corresponds to the directionalities of the entire panel (Figure 1) showing that
there are less privileged directions than the ladder or, equivalently, the full
panel has major entropy (i.e., the ladder has more precise information). (b)
Shows a histogram with the directionalities of the full panel. It is smoother
than the ladder because there are more curved designs. As mentioned, the
maximal strokes in the ladder (Figure 2(a)) are at 90o corresponding almost
to 20% of the total, whereas in the entire panel (Figure 2(b)), the maximal
strokes also at 90o reach only 6%. Consequently, the ladder contains more
specific directions than the full panel.

The ladder strokes, or traits, are not fully symmetric around 0o or 90o. In fact, traits are more frequent between 0o-90o (43%) than in the complementary range (30%) and indicating that the author was possibly right-handed.

Additionally, as occur for painting [13], entropy-information can be associated with histograms like Figure (2). It is not the focus in this work; nevertheless, the entropy associated with the ladder (Figure 2 (a)) is smaller than the entropy associated with the full panel (Figure 2 (b)). In this way, from the information theory standpoint, the ladder contains more precise information than the whole group.

A Topological Equivalent: A Route Map Proposal

The ladder shape in Figure 1 contains, in my view, still more practical information than provided in the above section. I suggest that it entails a schema for performing permissible actions or restricting approaches in the cave. In other words, it defines routes into the cavern. Figure 3(a) shows a schematic drawing of the cave (black font, https://en.wikipedia.org/wiki/Cave_of_La_Pasiega) with a virtual superimposed route map (red font, author suggestion). The black font schema contains three main obstacles (wall-rocks) every one forming around, necessarily, routes or passages. Other barriers are smaller and not designated in the figure.

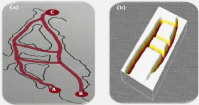
Figure 3: (a) A topographical depiction of the cave in La Pasiega (black font) with a virtual superimposed route map (red font) that is topologically equivalent to the ladder design. The full panel is located approximately at point A in the cave. Point C indicates the entrance to other tunnels, with an approximate distance of 25 meters between points A and C. Point B is spatially opposite to point A in the area of ample walking space. (b) A full schematic depiction of the ladder shown in Fig. 1 as a three-dimensional corridor and topologically equivalent to the virtual map (red font).

    

    
    

    

    Figure 3: (a) A topographical depiction of the cave in La Pasiega (black
font) with a virtual superimposed route map (red font) that is topologically
equivalent to the ladder design. The full panel is located approximately at
point A in the cave. Point C indicates the entrance to other tunnels, with
an approximate distance of 25 meters between points A and C. Point B is
spatially opposite to point A in the area of ample walking space. (b) A full
schematic depiction of the ladder shown in Fig. 1 as a three-dimensional
corridor and topologically equivalent to the virtual map (red font).

The ladder design and the virtual route map are topologically equivalent: each with five nodes and three enclosed areas (Figure 3a&b). Additionally, the 5:3:9 area-ratio mentioned previously corresponds approximately to walking spaces within each region of the cave.

Finally, the original design found in the cave is located roughly at point A in Figure 3(a) and, possibly, correlated with an entrance to the cavern.

Conclusion

The ladder-shaped design found in La Pasiega cave has various mathematical and geometrical properties. As suggested in this work, it corresponds to a signal of practical relevance (information).

The schema reveals a distribution of compositional strokes or traits with directionalities mainly at the 0o and 90o angles. The asymmetrical details around these two directional inclinations (Figure 2) suggest that the ladder’s composer was right-handed.

On my view, the ladder is topologically equivalent to a virtual main-route map within the cave (Figure 3). Consequently, if my view is right, the author of that schema possessed topographical abilities with social implications. Namely, a 65000 years old species with anthropological sense [14,15]. In fact, several works are devoted to joint mathematical aspect with social behaviors [14-25].

In brief, with some risk, I propose that the ladder design at La Pasiega cave contains the following info:

• The ratio of the spaces enclosed by the ladder (5:3:9) is possibly related to walking areas.

• Corridors or passages description. They are topologically equivalents to a map in the cave.

• Presumably point A, where the ladder was drawn (Figure (3)), is related to a cave-entrance at that epoch.

• Ladder Information-entropy is smaller than the full panel. Accordingly, the ladder contains more precise information.

Acknowledgement

Helpful discussions related to left or right-handed prehistoric painters were carried-out with Rodolfo Contreras Neira (Museo Augusto Capdeville, Taltal, Chile).

References

  1. Hoffmann DL, Standish CD, García-Diez M, Pettitt PB, Milton JA, Zilhão J, et al. U-Th dating of carbonate crusts reveals Neanderthal origin of Iberian cave art. Science. 2018; 359: 912-915.
  2. Pearce DG, Bonneau A. Trouble on the dating scene. Nat Ecol Evol. 2018; 2: 925-926.
  3. Hoffmann DL, Standish CD, García-Diez M, Pike AWG, Pettitt PB, Angelucci DE, et al. Dates for Neanderthal art and symbolic behavior are reliable. Nat Eco Evol. 2018; 2: 1044-1045.
  4. Appenzeller T. Old Masters. Nature. 2013; 497: 302-304.
  5. Ruebens K, McPherron SJP, Hublin JJ. On the local Mousterian origin of the Chatelperronian: Integrating typo-technological, chronostratigraphic and contextual data. J Hum Evol. 2015; 86: 55-91.
  6. Mellars P. Neanderthal symbolism and ornament manufacture: The bursting of a bubble?. P Natl Acad. Sci. 2010; 107: 20147-20148.
  7. Herrera KJ, Somarelli JA, Lowery RK, Herrera RJ. To what extent did Neanderthals and modern humans interact?. Biol Rev. 2009; 84: 245-257.
  8. Villa P, Roebroeks W. Neandertal demise: An archaeological analysis of the modern human superiority complex. PLOS ONE. 2014; 9: e96424.
  9. Jimenez-Espejo FJ, Martinez-Ruiz F, Finlayson C, et al. Climate forcing and Neanderthal extinction in southern Iberia: Insights from a multiproxy marine record. Quaternary Sci. Rev. 2007; 26: 836-852.
  10. Flores JC. Diffusion coefficient of modern humans outcompeting Neanderthals. J Theor Biol. 2011; 280: 189-190.
  11. Golovanova LV. Significance of ecological factors in the middle to upper Paleolithic transition. Curr. Anthropol. 2010; 51: 655-691.
  12. Roberts MF, Bricher SE. Modeling the disappearance of the Neanderthals using principles of population dynamics and ecology. Journal of archaeological Sciences. 2018; 100: 16-31.
  13. Flores JC. Entropy signature for cracks networks in old paintings: Saturation prospectus. Entropy. 2018; 20: 772.
  14. Grigolini P. Transition from biology to anthropology: A theoretical challenge. Austin Anthropology. 2019; 3: 1004.
  15. Marincovic S, Lazic D, Tomic I, Boljanovic J. The biological and social survival of humanity. A Review. Austin Anthropology. 2019; 3: 1005.
  16. Murray JD. Mathematical biology I: An introduction. Springer. 2002.
  17. Murray JD. Mathematical biology II: An introduction. Springer. 2002.
  18. Cantrell RS, Cosner C. Spatial ecology via Reaction-diffuions equations. Wiley. 2003.
  19. Vespignani A. Modelling dynamical process in complex technical systems. Nat Phys. 2012; 8: 32-39.
  20. Boccara N. Modeling Complex Systems. Second edition. Springer. Berlin. 2010.
  21. Lakshmanan M, Rajasekar S. Nonlinear Dynamics: Integrability, Chaos and Patterns. Springer. Berlin. 2003.
  22. Deloubrière O, Hilhorst HJ, Taüber UC. Multispecies pair annihilation reactions. Phys. Rev Lett. 2002; 89: 250601.
  23. Hilhorst HJ, Washenberger MJ, Taüber UC. Symmetries and species segregation in diffusion-limited pair annihilation. J Stat Mech. P10002. 2004.
  24. Roman C, Davydovych V. Non-linear Reaction-Diffusion systems. Springer. 2017.
  25. Valverde S, Ohse S, Turalska M, West BJ, Garcia-Ojalvo J. Structural determinants of criticality in biological networks. Front. Physiol. 2015; 6; 127.

Citation: Flores JC. A Route Map Proposal as the Topological Equivalent of the Ladder Design (65000 Years Ago) at La Pasiega Cave. Austin Anthropol. 2019; 3(2): 1011.