
Research Article
Austin Biochem. 2017; 2(1): 1010.
Density Function Theory and Hartree-Fock Study on the Electronic Structure of β-Sitosterol
Joginipelli S¹, Melapu VK¹ and Darsey J²*
¹Department of Computer Science, Jackson State University, USA
²Department of Chemistry, University of Arkansas at Little Rock, USA
*Corresponding author: Darsey J, Department of Chemistry, University of Arkansas at Little Rock, 2801 South University Avenue, Little Rock, AR, 72204, USA
Received: January 24, 2017; Accepted: May 17, 2017; Published: May 24, 2017
Abstract
In this study, a comparative Density Functional Theory (DFT) and Hartree- Fock (HF) calculations were preformed to understand the dynamic behaviour and bioactivity of β-Sitosterol (beta-Sitosterol) to gain insights about its electronic structural properties, and reactivity. This research article deals with theoretical study of structural and electronic properties such as Highest Occupied Molecular Orbitals (HOMO) and Lowest Unoccupied Molecular Orbitals (LUMO), molecular structure, energy surfaces, orbital energies, energy gap, electron affinity, ionization potential, vibrational spectra, of β-Sitosterol; a well-known natural product from medicinal plants. HOMO, LUMO of β-Sitosterol were generated and interpreted with Density Functional Theory (DFT) and Hartree-Fock (HF) calculations following full structure optimization. HOMO, LUMO generated with DFT and HF calculations were compared and a detailed visualization of orbitals and their energies were presented. Contour plots and energy maps were also generated, analyzed and interpreted for potential activity. The similarities and differences between the DFT and HF calculations for β-Sitosterol were studied and highlighted. Thermodynamic calculations were performed with the DFT methods using B3LYP/6-31G: PM3 level of theory.
Keywords: β-Sitosterol; Quantum mechanical calculations; ab-initio; Density Function Theory (DFT); Highest Occupied Molecular Orbitals (HOMO); Lowest Unoccupied Molecular Orbitals (LUMO); B3LYP; 6-31G; Hartree-Fock (HF)
Abbreviations
DFT: Density Functional Theory; HOMO: Highest Occupied Molecular Orbitals; LUMO: Lowest Unoccupied Molecular Orbitals; HF: Hartree-Fock
Introduction & Background
Throughout the ages, humans have relied on nature for their basic needs such as food, shelter, clothing, and medicines [1]. Due to the natural ability of plants to synthesize a wide variety of compounds, they have traditionally been used as source of medicines to cure a variety of ailments and to prevent disease. Countries with ancient civilization such as India, China, and Egypt historically used plants as remedies for various conditions and ailments [2]. Although many approved and clinical-trial drugs have been derived from natural products, the last 20 years has shifted the emphasis from natural products to less expensive synthetic products [3]. Many of these compounds have served as predecessors for modern drug therapies [3]. Advances in medicinal chemistry, in combination with multidisciplinary research, have expanded our understanding regarding the specifics of individual chemical constituents. Armed with this information, it has become possible to analyze and evaluate the active principles in natural products and plants that possess better drug properties, less toxicity, and better pharmacokinetics [4].
Chemical constituents such as β-Sitosterol, Sitosterol, Stigmasterol, Tectoquinone, Kaempferol, and Lygiodinolide found in Lygodium flexuosum plant have been linked to the prevention and delaying onset of symptoms Alzheimer’s disease. β-Sitosterol is one of the several phytosterols found in Lygodium flexuosum plant and is an anabolic precursor of Boldenone steroid. Lygodium flexuosum plant has high content of β-Sitosterol and the plant extract is used in the treatment of Alzheimer’s disease [5]. Phytosterols are a subgroup of the steroids, and are important class of bio-organic molecules widespread in plants, animals, marines and fungi. Pharmaceutical products and certain food materials have these compounds and are generally recognized as safe without undesirable side effects. Among phytosterols, β-Sitosterol is usually used for heart diseases, hypercholesterolemia, modulating immune system, prevention of cancer, as well as relieving symptoms of rheumatoid arthritis, tuberculosis, cervical cancer, and benign prostate hyperplasia. Due to the diverse biological activities β-Sitosterol was considered as one of the most important natural product that need to be analyzed to confirm its efficacy and safety [6]. β-Sitosterol was chosen to perform Quantum Mechanical calculations to gain insights about reactivity and electronic structural properties and β-Sitosterol molecule used in this study is not purified from Lygodium flexuosum plant. Quantum Mechanics (QM) stands out as a powerful computational approach to characterize the structure, dynamics, and reactivity of bio-molecules [7]. QM calculations to identify potent inhibitors are extremely attractive approaches mainly because of high accuracy (relative) to estimate structural properties [8]. The increasing popularity of quantum mechanical methods in Computer Aided Drug Design (CADD) is not just a consequence of growing computational power, but is due to the first principle nature of QM that provides highest accuracy [8]. Over the last two decades powerful molecular modeling tools have been developed that are capable of accurately predicting structural energetics, reactivity’s, and other electronic properties of molecules. These developments are due to dramatic increases in computer speed and design of efficient quantum chemical algorithms [9]. Quantum Mechanical studies particularly DFT and HF studies can evaluate a vast range of structural, chemical, optical, spectroscopic, elastic, vibrational and thermodynamic phenomena. The ability of DFT and HF calculations to predict structure-property relationships have improved and revolutionized experimental studies [10]. DFT and ab-initio quantum chemistry has become an essential tool in the study of atoms, molecules and complex systems. The underlying technology in DFT and HF study is providing a computational solution of the electronic Schrodinger equation; given the position of atomic nuclei and total number of electrons in the system, DFT and HF calculations will calculate the electronic energy, electron density, HOMO (Highest Occupied Molecular Orbitals), LUMO (Lowest Unoccupied Molecular Orbitals), electrostatic potential maps and other properties [11]. Graphical models from quantum mechanical studies, electrostatic potential maps, HOMO (Highest Occupied Molecular Orbitals), and LUMO (Lowest Unoccupied Molecular Orbitals) maps have proven of considerable value not only to rationalize trends in molecular structure, stability, chemical reactivity, and selectivity, but also as tools with which to carry out chemical investigations [12]. Electrons and their distribution in molecular orbitals are considered the most important factor to determine the reactivity of the molecule. For example, p surface of benzene with high electron density indicate electrophilic attack that occurs on Benzene at p face [12]. Chirality of potential drug molecules is essential to current pharmaceutical development process [13]. The physiological effects of different enantiomers are not often equivalent; in some cases, they have different physiological effects [13]. Sometimes two enantiomers of the same compound can be used to treat two separate medical conditions. For example, the (R, R) enantiomer of Ritalin is used to treat Attention Deficit Disorder (ADD) while the (S, S) enantiomer is an antidepressant [13]. Ab-initio quantum mechanical calculations including Density Functional Theory (DFT) calculations are computationally intensive but regarded as the most accurate approaches to theoretically calculate the structural properties of molecules [11].Quantum mechanical studies of chemical constituents from medicinal plants will provide insights into electronic structural properties, electron density, molecular orbitals, vibrational spectra, and chirality of the molecule.
The classes Density Functional Theory (DFT) formalism introduced by Hohenber, Kohn, and Sham in mid 1960’s is based on the idea of replacing complicated N-electron wave function with simpler 1-electron charge density in electronic structural calculations of the ground stationary states [14]. In this study, theoretical DFT calculations were performed on β-Sitosterol to gain insights into electronic structural properties. Density Function Theory is presently useful tool for extracting electronic energy states of molecules and is considered as one of the useful tools in quantum chemistry to calculate electronic structural properties. The electronic strucutral properties calculated with DFT is combination with B3LYP hybrid functional and the 6-31G basis set has been shown to provide accurate energies for excited states [14].
Materials and Methods
Quantum mechanical calculations
The molecular geometries of β-Sitosterol in their ground and excited states were optimized using the Gaussian 09 program package. DFT calculations were performed with optimized structures using B3LYP exchange correlation functional and 6-31G basis set. The calculations were used to evaluate electronic structural properties, chemical reactivity, and selectivity of molecules. Calculations were performed on the University of Arkansas at Little Rock (UALR) High Performance Computer Cluster servers; Argon, Erbium, and Boron using Gaussian 09 program [15]. DFT calculations were performed with 6-31G basis set and HOMO (Highest Occupied Molecular Orbitals), LUMO (Lowest Unoccupied Molecular Orbitals), density, electrostatic potential, Laplacian, and spin density cube files for surfaces were generated. The graphical models generated for HOMO and LUMO were visualized with Gauss-View 5 program [16]. Abinitio level calculations were performed with HF method, used to solve the time-independent Schrodinger equation for a multi-electron atom or molecule using 6-31G basis set. Calculations to calculate the total energy and dipole moment were also performed. The output file generated from Gaussian09 was used to visualize the electron density, electrostatic potential map, and HOMO, LUMO orbitals using GaussView5. The results of β-Sitosterol were visualized with Gauss view and were presented to analyze and interpret the potential medicinal activity.
By using HOMO and LUMO energy values for a molecule, chemical potential, electronegativity and chemical hardness can be calculated as follows [17]
Chemical Potential of the molecule given by
μ = (EHOMO + ELUMO) / 2
Chemical hardness of the molecule is given by
η = (ELUMO - EHOMO) / 2
Electronegativity of the molecule is given by
Χ = - (EHOMO + ELUMO) / 2
Results and Discussion
Quantum mechanical calculations for β-Sitosterol were carried out using the DFT method at the B3LYP/6-31G level of approximation. The optimized structure parameters of β-Sitosterol allowing the relaxation of all parameters, the calculations converge to optimized geometries, which correspond to the true energy minima, as revealed by the lack of imaginary frequencies in the vibrational mode. Quantum mechanical studies such as DFT and HF calculations were performed on chemical constituents obtained from Lygodium flexuosum with emphasis on β-Sitosterol. The HOMO, LUMO orbitals, mapped surfaces, contour plots, electro static potential surfaces, were calculated. Global chemical reactivity indices of all phytochemicals obtained were also compiled and archived. The calculated global chemical reactivity indices for each chemical compound include the HOMO, LUMO, energy gap, ionization potential, electron affinity, electro negativity, electrochemical potential, hardness, softness, electrophilicity in eV, total energy in A.U units, and dipole moment in Debye units. Frontier molecular orbital theory of explaining HOMO and LUMO surfaces was visualized with Gauss-view program using DFT calculations. Chemical structures of β-Sitosterol obtained from Lygodium flexuosum plant was shown with Gaussview. Figure 1 shows β-Sitosterol optimized chemical structure. From the structure, β-Sitosterol appears non-planar in the middle, all the energy contributions are positive and dominant contributions are due to dihedral, Van der waals, and angle interactions. The remaining contributions are relatively small. There is only one double bond in β-Sitosterol molecule, located in the middle of the ring. The c=c double bond is 1.34 Å, whereas the C-C single bonds vary between 1.48 and 1.55 Å. There is one oxygen atom in the present system; the C-O single bond length is 1.41 Å. C-H bonds are almost the same, ~1.11 Å, and the O-H bond is ~0.95 Å.
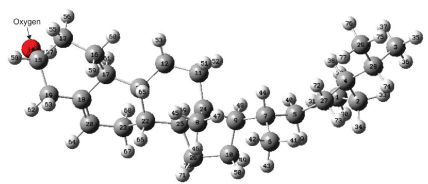
Figure 1: Chemical structure of β-Sitosterol, Ball and stick model with labels
of optimized structure Red: Oxygen; dark gray: Carbon; light gray: hydrogen
atoms.
Molecular orbitals with DFT and Hartree-Fock calculations
HOMO, LUMO orbitals were visualized and the energy gap was also calculated for each chemical constituent. HOMO and LUMO orbitals for β-Sitosterol were visualized using DFT and ab-initio calculations shown in (Figures 2, 3, 4, and 5) respectively. The frontier orbitals, HOMO and LUMO, determine the way the molecule interacts with receptors. The frontier orbital gap helps to characterize the chemical reactivity and kinetic stability of chemical structure. A molecule with larger orbital gap is more polarized in having a more reactive component. HOMO of β-Sitosterol with DFT calculations (Figure 2) is found over the whole molecule, HOMO obtained from ab-initio shows high reactivity on the rings (Figure 3), LUMO orbitals with DFT are located over the entire molecule (Figure 4) whereas the LUMO’s with ab-initio are present at the peripheral part of the side chain of the chemical structure (Figure 5). HOMO and LUMO energy difference has been calculated as ~6.8 eV. The HOMO-LUMO energy gap shows kinetic stability of the molecule; large gap indicate difficulty in adding electrons to high LUMO and remove electrons from a deep HOMO. The calculated dipole moment of the molecule is ~2.5 debye units. The dipole moment comparable to polar molecules and is considered as polar molecule.
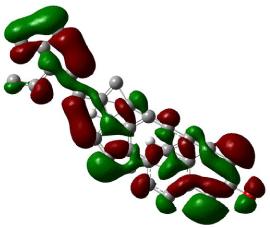
Figure 2: The isosurface of HOMO orbitals of β-stiosterol generated with DFT
method using B3LYP/6-31G level of approximation using Gaussian 09, and
visualized with Gauss view. The HOMO isosurface of β-Sitosterol consists
of green and red; green represents positive isosurface and red represents
negative isosurface.
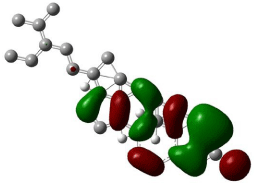
Figure 3: The isosurface of HOMO orbitals of β-Stiosterol generated with
Hartree-Fock calculations using Gaussian 09, and visualized with Gauss
view. The HOMO isosurface of β-Sitosterol consists of green and red; green
represents positive isosurface and red represents negative isosurface.
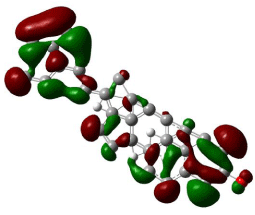
Figure 4: The isosurface of LUMO orbitals of β-stiosterol generated with DFT
method using B3LYP/6-31G level of approximation using Gaussian 09, and
visualized with Gauss view. The HOMO isosurface of β-Sitosterol consists
of green and red; green represents positive isosurface and red represents
negative isosurface.
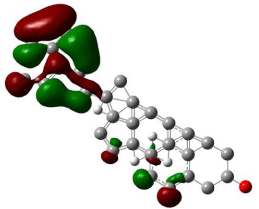
Figure 5: The isosurface of LUMO orbitals of β-stiosterol generated with
Hartree-Fock calculations using Gaussian 09, and visualized with Gauss
view. The HOMO isosurface of β-Sitosterol consists of green and red; green
represents positive isosurface and red represents negative isosurface.
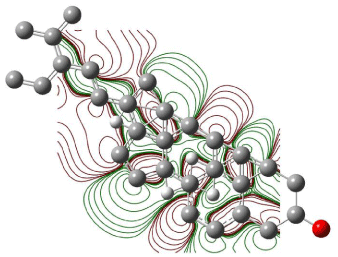
Figure 6: Contour plot of HOMO orbitals of β-Sitosterol.
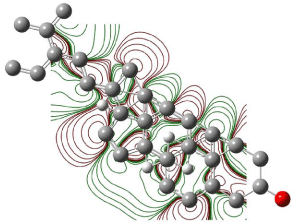
Figure 7: Contour plot of LUMO orbitals of β-Sitosterol.
Energy gaps and contour plots of β-Sitosterol
Excitation energies and oscillator strengths were calculated, three excitation states were explored, and excitation energies for excited state one calculated to be 0.0459 eV, for excited state two 0.3294 eV, and for excited state three 0.4185 eV. Geometry optimization was also performed for all the chemical constituents. The HOMO-LUMO energy gap was also explored. HOMO orbital 94 energy was 0.21156 eV and LUMO orbital 93 energy was 0.23226 eV. Figure 6 shows the contour plot of β-Sitosterol.
β-Sitosterol has stretching frequencies higher than the corresponding bending frequency, i.e., it is easier to bend a bond than to stretch or compress. Bonds to hydrogen have higher stretching frequencies than those with heavier atoms. Double bonds have higher stretching frequencies than the single bonds, as well as hashed and wedged bonds.
The electronegative lines form a closed contour that clearly indicates the total flux passing between these curves is not equal to zero. For any nucleophilic substitution, an amount of energy equal to shielded potential energy surface is required. Figures 6 & 7 show the contour plots of HOMO and LUMO orbitals of β-Sitosterol. There is no closed contour observed in the contour maps of HOMO and LUMO (Figures 6 and 7) around oxygen indicating a nucleophilic substitution reaction can occur at the site.
The mapped surfaces of β-Sitosterol HOMO, LUMO orbitals with DFT, and HF calculations shown in (Figures 8, 9, 10 and 11) respectively. Electrostatic potentials were mapped on the surface and colour coded to represent high and low electrostatic energies (Blue and green represents high electrostatic potential energies). The mapped surfaces HOMO and LUMO orbitals of β-Sitosterol covered the entire molecule based on DFT calculations as shown in (Figures 8 and 9), whereas the mapped surfaces of HOMO’s was concentrated on the rings and on the oxygen (Figure 10), and reactive surfaces were concentrated on the side chain of LUMO’s (Figure 11) based on HF calculations.
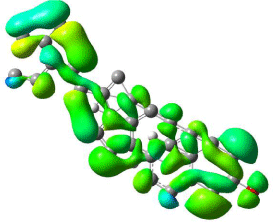
Figure 8: Mapped HOMO orbital surface of β-Sitosterol using DFT
calculations. High electrostatic energy surface shown in green.
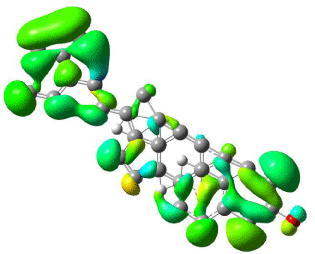
Figure 9: Mapped LUMO orbital surface of β-Sitosterol using DFT method
using B3LYP/6-31G level of approximation. High electrostatic energy surface
shown in green colour.
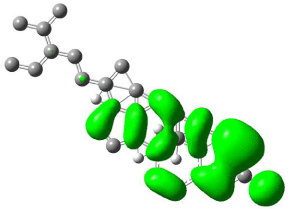
Figure 10: Mapped HOMO orbital surface of β-Sitosterol using Hartree-Fock
calculations. High electrostatic energy surface shown in green.
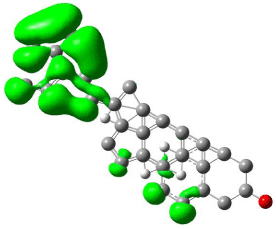
Figure 11: Mapped LUMO orbital surface of β-Sitosterol using Hartree-Fock
calculations. High electrostatic energy surface shown in green.
Conclusion
In present work, we have used density functional theory and Hartree-Fock methods to investigate the geometries and electronic structural properties of β-Sitosterol. Geometric parameters, vibrational frequencies, frontier molecular orbitals, molecular electrostatic potential plots and surfaces of β-Sitosterol were calculated using the DFT method at the B3LYP/6-31G level. The lower frontier orbital gaps show that β-Sitosterol have less kinetic stability and can be termed as highly reactive molecule. However, the higher value of dipole moment shows that it is highly polar. DFT and HF calculations on each chemical constituent from medicinal plants provided insights into the reactivity, excitation energy, total energy, dipole moment, and vibrational spectra of the molecules. DFT calculations with B3LYP/6-31G and geometry optimization revealed molecular geometry and steric repulsions β-Sitosterol of molecule. Ab-initio calculations using the HF/6-31G method gave optimized geometries for each conformer. HOMO and LUMO orbitals for chemical constituent with their orbital gap have been calculated and explored for reactivity. Contour plots were also explored to learn the nucleophilicity and electrophilic substitution reactions for the chemical compound. The molecular geometry of β-Sitosterol produced with HF and DFT methods with the HF method yielding better results when compared to the DFT method. Most of the calculated geometrical parameters increased in the order of HF, B3LYP, reflecting the correlation strength of the individual theories. Good results with HF indicates the applicability of HF method to large-scale applications for vibrational analysis of similar molecules.
Acknowledgement
This project was supported by grants from the National Center for Research Resources (5P20RR016460-11) and the National Institute of General Medical Sciences (8 P20 GM103429-11) from the National Institutes of Health. Also the Center for Molecular Design and Development (CMDD) at the University of Arkansas at Little Rock (UALR) provided molecular modeling software and high performance computers.
References
- Gurib-Fakim A. Medicinal plants: Traditions of yesterday and drugs of tomorrow. Molecular Aspects of Medicine. 2006; 27: 1-93.
- Sharma SC, SA Ahmad. Traditional medicinal plants: ancient and modern approach. Ancient Science of Life. 1992; 12: 197-200.
- Gerwick WH, BS Moore. Lessons from the past and charting the future of marine natural products drug discovery and chemical biology. Chemical Biology. 2012; 19: 85-98.
- Ntie-Kang F, Lifongo LL, Mbah JA, Owono LC, Megnassan E, Mbaze LM, et al. In silico drug metabolism and pharmacokinetic profiles of natural products from medicinal plants in the Congo basin. In Silico Pharmacology. 2013; 1: 12.
- Ros MM, Sterk SS, Verhagen H, Stalenhoef AF, de Jong N. Phytosterol consumption and the anabolic steroid boldenone in humans: a hypothesis piloted. Food Addit Contam. 2007; 24: 679-684.
- Ju YH, Clausen LM, Allred KF, Almada AL, Helferich WG. β-Sitosterol, β-Sitosterol Glucoside, and a Mixture of β-Sitosterol and β-Sitosterol Glucoside Modulate the Growth of Estrogen-Responsive Breast Cancer Cells In Vitro and in Ovariectomized Athymic Mice. The Journal of Nutrition. 2004; 134: 1145-1151.
- Peters MB, K Raha, KM Merz. Quantum mechanics in structure-based drug design. Curr Opin Drug Discovery and Development. 2006; 9: 370- 379.
- Liao C, Sitzmann M, Pugliese A, Nicklaus MC. Software and resources for computational medicinal chemistry. Future medicinal chemistry. 2011; 3: 1057-1085.
- Menikarachchi LC, Gascon JA. QM/MM approaches in medicinal chemistry research. Current Topics in Medicinal Chemisty. 2010; 10: 46- 54.
- Hasnip PJ, Refson K, Probert MIJ, Yates JR, Clark SJ, Pickard CJ. Density functional theory in the solid state. Philosophical transactions of the Royal Society a Mathematical, physical, and engineering sciences. 2014; 372: 20130270.
- Friesner RA. Ab initio quantum chemistry: Methodology and applications. Proceedings of the National Academy of Sciences of the United States of America. 2005; 102: 6648-6653.
- Hehre WJ. A Guide to Molecular Mechanics and Quantum Chemical Calculations. Wave function Inc. 2003.
- Nguyen LA, H He, C Pham-Huy. Chiral Drugs: An Overview. International Journal of Biomedical Science: IJBS. 2006; 2: 85-100.
- Huix-Rotllant, Casida ME. Progress in Time-Dependent Density- Functional Theory. Annual Review of Physical Chemistry. 2012; 63: 287- 323.
- Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J.R.Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT. 2009.
- GaussView, Version 5, Roy Dennington, Todd Keith and John Millam, Semichem Inc. Shawnee Mission KS. 2009.
- Pearson RG. Absolute electronegativity and hardness correlated with molecular orbital theory. Proceedings of Natural Academic Sciences. 1986; 83: 8440-8441.