Bactericidal and Therapeutic Effects of Pure Non-Pasteurized Honey on Mycobacterium avium Subspecies Paratuberculosis

Over the last decade there has been increasing enthusiasm for optical methods of probing and controlling excitable tissues, including optogenetics, optical uncaging, and infrared neural stimulation. Each of these methods has respective advantages and disadvantages that make them well suited for different applications. We have focused on the application of pulsed infrared light as a spatially-precise, noncontact, and artifact-free form of neural control [1]. We have shown that the pulsed temperature transients induced by spatially confined infrared pulses are capable of both eliciting and inhibiting action potential propagation [1,2]. We also showed that sub-threshold infrared and electrical stimulation can be combined to evoke a neural response [3,4]. While the complete mechanism of infrared induced activation is yet to be elucidated and a comprehensive model is still lacking, previous studies showed that a thermally-mediated change in electrical capacitance of the plasma membrane plays a key role [5]. Here we offer a plausible, simplified explanation for how infraredinduced temperature transients are applied towards both hybrid electro-optical stimulation and infrared inhibition.

Previous studies indicate that any model of interactions between infrared light and neural tissue must account for the induced temperature rise [5,6]. At its most basic level, this includes accounting for temperature changes in the Hodgkin-Huxley (HH) model of action potential initiation and propagation [7]. The HH model introduced gating variables to express the time and voltage dependence of the ionic conductances in the squid giant axon. The equation for the potassium conductance is:

where (conductance/cm²) is a constant and n is the dimensionless gating variable ranging from 0 to 1 that indicates the portion of molecules in a certain position (e.g. inside of the membrane). Similarly, the sodium conductance is given by:

where m is the portion of hypothetical activating molecules on the inside of the membrane and h is the proportion of activating molecules on the outside. Each gating variable is time, voltage and temperature dependent, and is modeled by:

where α_n and β_n are the opening and closing rates of the gates and k is a thermal coefficient(8). Equation (3) is also used to model the other gating variables (i.e. m and h). Frankenhaeuser and Huxley extended the original HH equations to myelinated fibers, which involved slight variations to equations (1) and (2), as well as the addition of a delayed non-specific ionic current, i_P, and its gating variable p [8,9].

The thermal coefficient, k, in equation (3) determines the acceleration of the opening and closing rates for each gate as the temperature deviates from a predetermined baseline [8]. k is determined by

Where T is the actual temperature and Q₁₀ is a constant used to quantify rate acceleration for a 10 °C increase in temperature. Hodgkin et al. found that a Q₁₀of 3 would allow for comparisons across temperature [10]. However, a Q₁₀ of 3 will not simulate an action potential in mammalian axons at 37 °C. Thus, accurate simulations matching empirical results require distinct temperature coefficients for each α and β [8,11]. To model empirical results accurately, the temperature coefficients for the n, h and p rate constants are all close to 3, while the m rate constants are approximately half that. Thus, as the nerve temperature increases, the rates of sodium inactivation (h) and potassium activation (n) overtake the rate of sodium activation (m). This results in an action potential that is either faster and weaker, or completely and reversibly blocked [12,13].

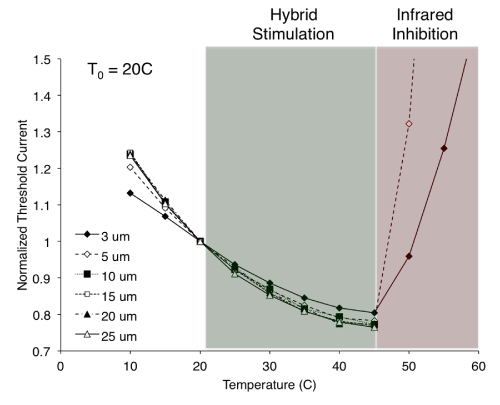
Understanding how this increase in temperature (as induced by a laser pulse) both enhances and inhibits the nerve’s response to electrical stimulation requires a closer look at the relationship between nerve temperature and the threshold electrical current for stimulation. Figure 1 shows the results of modeling simulations investigating how electrical stimulation threshold changes with temperature for various nerve fiber diameters. NEURON software (version 7.2) was used to model the myelinated Xenopuslaevis sciatic nerve and simulate the response to an extracellular electrical point stimulus [11,14]. The temperature of the node of Ranvier directlybeneath the electrical stimulus was adjusted independent of all other nodes and internodes to reflect the temperature change resulting from an ideally targeted infrared pulse [11]. Temperature coefficients were the same as those used by Mou et al. [11]. When the temperature of the node was increased to 45 °C (with T₀ = 20 °C), the threshold current for an electrically initiated action potential occurring at that node was reduced by up to ~20%. Hybrid electro-optical stimulation as we previously demonstrated is likely the result of this temperature increase [3,4,15]. In those studies, the electrical stimulation threshold was first found at baseline temperature (T₀) and then subsequently reduced to 90% of threshold. Providing a concurrent increase in nerve temperature via infrared laser exposure reduces the requisite current for stimulation, thus achieving hybrid activation with a previously sub-threshold electrical stimulus. However, if laser exposure is such that the node temperature surpasses a certain threshold (45 °C for these modeling studies), electrically initiated axonal activation will be blocked. Above 45°C, axons ≥ 10 μm in diameter were unable to elicit a propagating action potential at currents many times greater than threshold at T0. Axons ≤ 5 µm in diameter were still able to elicit propagating responses, though they required currents that were often much greater than at T₀. These results are in agreement with those presented by Mou et al. showing that larger diameter fibers (or higher stimulus currents) allowed for lower blocking temperatures [11]. This phenomenon offers an explanation for the inhibitory results we showed previously [2,4]. Thus there appears to be a critical infrared (or otherwise) induced temperature that divides the nerve’s response into two regimes: below the critical temperature the electrical stimulation threshold is reduced to produce hybrid electro-optical stimulation; above the critical temperature the axonal initiation of action potentials is inhibited.

Figure 1: A critical temperature divides an axon’s response to electrical stimulation. Simulations reveal that below the critical temperature (green shaded region), electrical stimulation threshold is reduced compared to baseline nerve temperature (T0 = 20 °C). This provides an explanation for hybrid electro-optical stimulation, whereby pulses of infrared light delivered concurrently with electrical stimulation create transient increases in nerve temperature and achieve neural activation with electrical currents that are less than what is required at baseline nerve temperature. Above the critical temperature (red shaded region), stimulation threshold currents for small diameter fibers are greatly increased, while larger diameter fibers are unable to evoke any response. This reflects infrared inhibition, where electrically initiated axonal activation is reversibly blocked by laser-induced transient increases in nerve temperature. Not shown are the normalized threshold  currents at 55 °C for the 5 μm axon (2.55) and at 60 °C for the 3 and 5 μm axons (1.63 and 3.99, respectively).