X-Ray Fan-Beam Luminescence Tomography

Review Article

X-Ray Fan-Beam Luminescence Tomography

Wenxiang Cong and Ge Wang*

Biomedical Imaging Center, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, USA

*Corresponding author: Ge Wang, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, 110 8th Street, Troy, New York 12180, USA.

Received: June 10, 2014; Accepted: October 10, 2014; Published: October 10, 2014

Citation: Cong W and Wang G. X-Ray Fan-Beam Luminescence Tomography. Austin J Biomed Eng. 2014;1(5): 1024. ISSN: 2381-9081.

Abstract

Nanophosphors emit near-infrared (NIR) light upon x-ray excitation, and can be functionalized as probes for in vivo molecular imaging. X-ray luminescence imaging maps a distribution of nanophosphors for diagnostic and therapeutic purposes. In this paper, we propose an x-ray fan-beam luminescence tomography approach to quantify a spatial distribution of molecular probes. A practical system is designed for x-ray fan-beam luminescence imaging in which an x-ray tube is collimated into a fan-beam of x-rays to excite nanophosphors on a cross-section through an object. The excited nanophosphors emit NIR light to be detected on the external surface of the object. The measured NIR light signal (2D) is used to reconstruct nanophosphors distribution on the cross-section (2D) of the object. In this imaging mode, the dimensionality of measurable data matches to that of the distribution of nanophosphors being excited, allowing an accurate and reliable image reconstruction. Numerical experiments are performed to demonstrate the feasibility and merits of the proposed approach.

Keyword: Optical molecular imaging; Nanophosphor imaging; Image reconstruction; Compressive sensing

Introduction

Nanoparticles are typically smaller than several hundred nanometers in size, comparable to large biological molecules. Nanoparticles offer various possibilities to develop new therapeutic and diagnostic tools. Biomolecules can be conjugated to nanoparticles through surface functional groups, such as targeting ligands for cell specific binding. With dimensions on the nanoscale, nanoparticles can go through microvasculature and across various biological barriers to reach biological targets [1, 2]. While nanoparticle-based therapeutic systems can effectively deliver drugs to disease sites, molecular imaging provides spatial and temporal information of molecular targets [3].

The nanoparticles as optical probes are important for in vivo molecular imaging to visualize biological processes at molecular and cellular levels in living systems [4,5]. Nanophosphors are light-emitting materials with stable optical properties, and emit near-infrared (NIR) luminescence light upon x-ray excitation. Recent results suggest that lanthanide-doped nanoparticles absorb x-ray radiation and emit in the visible to near infrared spectrum via a down-conversion mechanism, making them a potentially valuable agent for in vivo imaging studies. A series of Gd3+ and Eu3+compositions in lanthanide fluorides were employed to optimize the emission from Eu3+ upon x-ray excitation [6]. Using the nanophosphors, x-ray luminescence computed tomography (XLCT) was recently proposed using an x-ray pencil beam excitation in the first generation CT scanning mode [7,8]. Through selective excitation with a pencil x-ray beam, XLCT can perform in vivo tomographic imaging on a region of interest (ROI). The classic CT methods can be applied to reconstruct an image, with spatial resolution defined by the x-ray pencil beam aperture. This x-ray stimulated luminescence imaging scheme acquire information about tissue anatomy and nanophosphor probes in one scan. The use of x-ray excitation also eliminates autofluorescence in optical fluorescence imaging, and the straight line propagation of x-rays in a biological object has a localized and deep probing capability. However, this imaging mode is similar to a conventional first generation CT scan, needs long data acquisition time, and has a limitation for most preclinical applications. To enhance the scanning efficiency, a cone beam x-ray luminescence computed tomography strategy was proposed [9]. In the cone beam imaging mode, x-rays illuminate a whole object to stimulate all the nanophosphors in an object, and a CCD camera acquires luminescent signal on the surface of the object. Clearly, this cone beam mode significantly reduces scanning time. However, it does not sufficiently utilize x-ray based source localization for image reconstruction. In this paper, we propose an x-ray fan-beam luminescence tomographic imaging method to reconstruct light-emitting nanophosphors slice by slice. Our method can achieve fast data acquisition and reliable image reconstruction at the same time.

Imaging Methodology

Imaging system

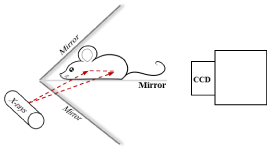
Nanophosphors can be functionalized as probes, which are introduced into a biological object such as a small animal for in vivo molecular imaging [3]. When an x-ray irradiates the object, the nanophosphors are excited to emit Near-Infrared (NIR) light. An imaging system is here designed to acquire the light signal on the external surface of the object for image reconstruction of nanophosphors. The system consists of a common x-ray tube, a highly sensitivity EMCCD camera, two mirrors at a right angle, and stages. A mouse is prostrate on a transparent mirror positioned between the two mirrors. The mirror setup is intended to expand the field of view of the camera by acquiring two views of the mouse simultaneously. The EMCCD camera is mounted on a horizontal linear stage on an optical table to change the focal plane without manipulating the lens. The x-ray tube sends a fan-beam of x-rays towards the mouse, to excite a cross-section of the animal. The x-ray tube is on a motorized vertical linear stage to excite a different cross-section as needed. The system is controlled by a custom-made LabVIEW program. The whole system is housed within a light tight box constructed with aluminum posts and aluminum panels painted matte black to minimize light reflection. The top-level system design is shown in Figure 1. The acquired NIR light signals on the external surface of the object form a two dimensional dataset, which are used to reconstruct an excited cross-section of the animal. Importantly, the dimensionality of measurable data matches to that of the image of excited nanophosphors to be reconstructed, allowing an accurate and reliable imaging performance.

Light transport model

The x-rays coming from the x-ray tube are collimated to a fan-beam using a lead collimator. Nanoparticle emission relies on the x-ray intensity distribution. By the Lambert-Beer law, the intensity distribution of the x-rays on a cross-section in the animal can be computed as

X (r) = X_{0} \exp (- \int_{0}^{| r - r_{0} |} μ (r_{0} + t \cdot \frac{r - r_{0}}{| r - r_{0} |}) d t) (1)

where r₀ is an x-ray source position, X₀ the incident x-ray intensity, μ the linear attenuation coefficient of the imaging object which can be computed from an attenuation-based computed tomography (CT) scan, and r locates on the cross section of a region of interest (ROI) in the animal, which is determined by the x-ray fan-beam.

The surface of an animal is well represented in a finite element mesh. The measured data can be mapped to surface elements and converted to photon fluence rates using an interpolation method. The cross section can be discretized using spatial triangular elements on each of which a variable is assigned to reflect nanophosphor emission. The element size is related to spatial resolution of image reconstruction. The photon fluence rate at each surface element is contributed from potential light sources, nanophosphor emission, and x-ray flux. The photon fluence rate recorded by each detector element is a linear combinations of nanophosphor emissions from all the elements on the cross section. Optical radiative transport equation (RTE) or Monte Carlo simulation (MC) can accurately trace photon propagation in a biological object [10]. Thus, a linear equation system can be established to describe the relationship between photon fluence rates at surface elements and the photon emissions at spatial elements on the cross-section of the animal [11,12]:

Φ = A \cdot S (2)

where Φ is a vector of the photon fluence rates at surface elements obtained from measurement, S a vector of light source intensities on spatial elements on the cross-section, and A the system matrix, its each column vector consists of photon fluence rates on surface elements contributed by the nanophosphors emission at a corresponding spatial element on the cross-section. Nanoparticle emission depends on the nanophosphor concentration ρ(r), x-ray intensity X(r), and light yield ε which is defined as the quantum yield per unit nanophosphor concentration and can be experimentally determined [13]:

S (r) = ε X (r) ρ (r) (3)

From Eq. (2-3), we have a linear equation system with respect to the nanophosphor concentration distribution ρ(r):

A \cdot (ε X \cdot ρ) = Φ (4)

Image reconstruction

Since the measured data are corrupted by noise, it is not practical to directly solve the system Eq. (4). The nanophosphor concentration distribution ρ can be effectively reconstructed using an optimization method. In terms of the biological characteristics encountered in the pre-clinical applications, nanoparticles are selective, often attached to certain types of cells, and accumulate to specific spots in the tissue, forming a sparse distribution. Hence, a compressive sensing (CS) reconstruction technique can be applied to achieve an accurate and stable solution from far less data [14]. With CS, we can convert the reconstruction problem to the following l₁ norm minimization problem:

\begin{matrix} \begin{matrix} \min i m u m & {‖ ρ ‖}_{1} \end{matrix} \\ \begin{matrix} s u b j e c t & \begin{matrix} t o & A \cdot (ε X \cdot ρ) = Φ \end{matrix} \end{matrix} \\ ρ \geq 0 \end{matrix} (5)

The presence of the l₁ term is used to induce the solution sparsity. This optimization problem Eq. (5) can be transformed to an unconstraint optimization using am interior-point method. Then, the preconditioned conjugate gradients (PCG) algorithm is used to compute the search direction for truncated Newton iterations. This strategy can efficiently solve large-scale sparse problems with a million variables in a few tens of minutes on a PC [15].

Numerical Experiments

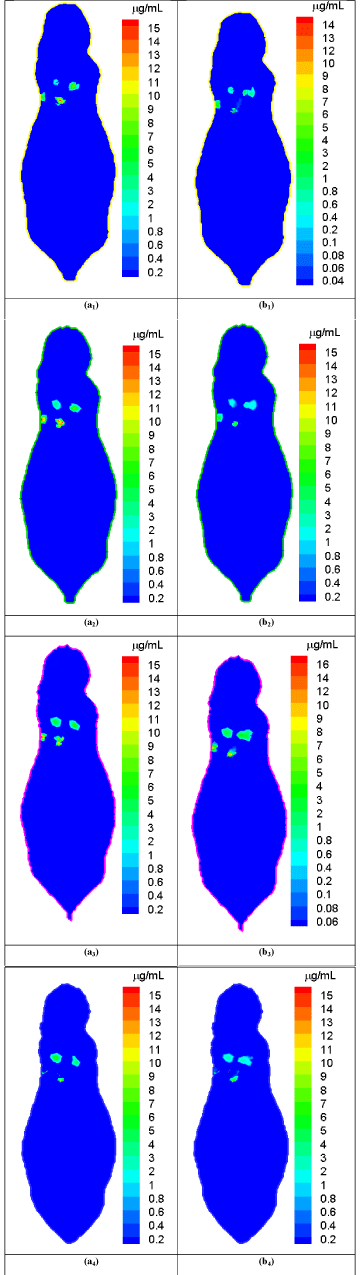
We performed representative numerical tests to evaluate the proposed approach with a digital mouse phantom. The mouse phantom was established from CT slices of a mouse using Amira (Amira 4.0, Mercury Computer Systems, Inc. Chelmsford, MA, USA) [16]. The phantom was discretized into 306773 triangular elements, 58244 nodes, 32324 surface elements [17]. Biologically relevant optical parameters were assigned to the phantom: absorption coefficient μ_a=0.02mm^-1, scattering coefficient μ_s=15mm^-1, and anisotropy parameter g=0.9. An x-ray tube was operated at 50 keV and 5 mA and collimated into a fan beam of a 1.5mm thickness. The nanophosphors distributed in the mouse lung region with different concentrations from 8.0μg/mL to 16.0μg/mL, and accumulated at four locations centered at (17.0 32.5 11.5), (21.0 37.0 11.5), (22.0 32.0 11.5), and (26.0 36.0 11.5) respectively. We used a Monte Carlo simulator to simulate NIR light propagation, and recorded NIR light intensities at surface elements of the phantom. The acquired NIR data was corrupted by Poisson noise to simulate practical conditions. The proposed reconstruction method was employed to reconstruct the nanophosphor concentration distribution from the NIR dataset. We selected cross-sections at the transverse positions of 11mm, 11.5mm, 12mm, and 12.5mm in the mouse phantom and respectively reconstructed the nanophosphor distributions. Figure 2 shows the comparisons between the true and reconstructed nanophosphor concentration distributions on the cross-sections at the transverse positions of 11mm, 11.5mm, 12mm, and 12.5mm in the mouse, respectively. The reconstructed images were in excellent agreement with the truth. The relative error $\frac{1}{N u m (k | ρ_{k}^{t} > ε)} \sum_{ρ_{k}^{t} > ε} \frac{ρ_{k}^{r} - ρ_{k}^{t}}{ρ_{k}^{t}}$ was used to quantify the reconstruction accuracy, where ρ^t_k and ρ^r_k are the true and reconstructed concentrations on the k-th mesh element, respectively, ε is a background noise level with a value of 0.1μg/mL, and $N u m (k | ρ_{k}^{t} > ε)$ the number of elements in the set ${k : | ρ_{k}^{t} > ε}$ The relative errors of the reconstructed images are &l25%.

Discussions and Conclusion

We have proposed a practical x-ray fan-beam luminescence imaging system and a reconstruction method to quantify a concentration distribution of nanophosphors in a biological object. The simulation results have demonstrated the feasibility and potential of the proposed approach. This x-ray fan-beam luminescence imaging mode performs the image reconstruction of nanophosphors slice by slice, efficiently utilizing the x-ray characteristics of straight line propagation in a biological object. It is underlined that our approach allows the best dimensionality match between measured data and excited voxels (2D-to-2D), while the pencil beam and cone-beam scanning modes are not in a good balance (2D-to-1D and 2D-to-3D respectively), allowing an accurate and reliable image reconstruction. As a result, an optimal balance between accuracy and efficiency is achieved with our approach, outperforming the popular bioluminescence and fluorescence tomography methods. The x-ray fan-beam luminescence tomographic imaging modality may find pre-clinical applications in monitoring drug delivery, assessing cancer therapy and other applications. Further in vivo experiments will be reported in the future.

References

Figure 1

X-ray fan-beam luminescence tomography system diagram.

Figure 2

Comparison between the true and reconstructed nanophosphor distributions.

(a₁)-(a₄) are the true nanophosphor concentration distributions on the transverse positions of 11mm, 11.5mm, 12mm, and 12.5mm in the mouse, respectively. (b₁)-(b₄) are the reconstructed nanophosphor concentration distributionson the transverse positions of 11mm, 11.5mm, 12mm, and 12.5mm in the mouse, respectively

Imaging Methodology

Numerical Experiments

Discussions and Conclusion

References

Review Article