Ao Yuan; Xiaogang Zhong; George E Bonney

Research Article

Austin Biom and Biostat. 2014;1(1): 7.

A Likelihood Model for Linkage Analysis of Genetic Traits

Ao Yuan¹*, Xiaogang Zhong¹ and George E Bonney²

¹Department of Biostatistics, Bioinformatics and Biomathematics, Georgetown University, USA

²National Human Genome Center, Howard University, USA

*Corresponding author: Ao Yuan, Department of Biostatistics, Bioinformatics and Biomathematics, Georgetown University, Washington, DC 20057, USA.

Received: August 18, 2014; Accepted: September 09, 2014; Published: September 22, 2014

Abstract

Linkage analysis is one of the major approaches for genetic studies of human diseases, for mapping putative genes or studying relationships between loci. Many of the existing methods use identity by descent data, or a particular familial structure, which may not be fully available in some practices. Here we propose a likelihood model for linkage analysis with pedigrees, along with segregation and regressive analysis. Without requiring identity by descent data, this model can be used for both quantitative and qualitative traits to study trait-trait linkage with/without observed genotypes, or trait-marker linkage with observed marker genotype, which include sib pair analysis as a special case. This model is applied to a real data example for illustration.

Keywords: Gamet; Gene loci; Linkage; Recombinant fraction

Introduction

The advances in biotechnology have led to the identification of more and more disease genes without the knowledge of the biochemical nature of the diseases. Linkage analysis is one of the most commonly used approaches for mapping human disease genes, which is often the first step to identify the chromosomal location of them, and may followed by various diagnosis and ultimately therapeutic treatment for these diseases. There are numerous methods, parametric, nonparametric and semi-parametric, for link- age/ association analysis [1-6]. Furthermore Kruglyak et al. [7] proposed a unified multipoint approach, Hor- vath et al. [8] considered family based approach for this problem, Sung et al. [9] suggested a multipoint analysis using Markov chain Monte Carlo algorithm. Many of them use the Identity by Descent (IBD) data, or require some particular familial structure such as infected relative pairs or extreme discordant sib pairs. But in practices IBD data cannot be uniquely determined or not fully available, and particular familial structure are difficult to collect, while marker genotyping data are commonly available. Many of these models are not for the study of trait-trait genetic relationship; some of them use only part of the data information, for example the squared trait value difference. Although robust, the nonparametric model-free methods may suffer potential loss of efficiency since they do not use knowledge of traits generating mechanism. In addition, complex traits are often affected by covariates such as sex, age, race and environmental factors. Here we consider a simple likelihood model for linkage analysis for pedigrees, along with segregation and covariates analysis based on the likelihood principle. This model can be used to study trait-trait linkage with/without observed genotypes, or trait-marker linkage with observed marker genotype, which include sib pair analysis as a special case. Using this model as an illustration, we analyze a set of nuclear family data to reveal the genetic connection of two traits which are known have close phenotypic relationships. Some possible extension of future work is discussed.

Methods

We describe the method for quantitative traits and nuclear family, the cases for qualitative traits or combined traits are similar, the general pedigree case can be analyzed by breaking it into nuclear families. Let y_f, y_m and y_o be d-dimensional observations of the father, mother and off spring respectively, where

y_{f} = {(y_{f, 1}, .., y_{f, d})}^{T}, y_{m} = {(y_{m, 1}, .., y_{m, d})}^{T},

y_{o} = {(y_{1}, .., y_{n})}^{T}, y_{j} = {(y_{j, 1}, .., y_{j, d})}^{T}, (j = 1, ..., n)

and n is the number of sibs in the nuclear family. Denote y = (y_f, y_m, y_o)^T and its underlying random variable by Y = (Y_f, Y_m, Y_o)^T. Let L₁ and L₂ be the two loci under consideration for linkage analysis, we assume there are two alleles at each locus, with a₁|b₁ for L₁ and a₂ |b₂ for L₂. We code the genotype at each locus as 0, 1 and 2 for b|b, a|b (b|a) and a|a respectively, r be the recombinant fraction - the probability that a gamet is recombinant, n be the sib size for the family. Let g_fi, g_mi and g_ji be the genotypes of father mother and the j-th sib at locus i (i = 1, 2), p_1i and p_2i be the proportion of the corresponding genotype at locus i. Let p_ij be the proportion of the haplotype

(\frac{g_{i}}{g_{j}}), (i, j = 0, 1, 2), g_{f} = (\frac{g_{f 1}}{g_{f 2}})

g_{m} = (\frac{g_{m 1}}{g_{m 2}}), g_{j} = (\frac{g_{j 1}}{g_{j 2}}), T (g_{j} | g_{f}, g_{m})

be the transmission probability of the sibs genotype given those of the parents. Note that there are 9 possible composite genotypes at the two loci for each individual. Consider the multivariate model and the notations as in Yuan and Bonney [10], assume unknown phase, the likelihood for a given nuclear family can be written as

L (y) = \sum_{g_{f}} P (g_{f}) f (y_{f} | g_{f}) \sum_{g_{m}} P (g_{m}) f (y_{m} | y_{f}, g_{f}, g_{m}) K (g_{f}, g_{m})

\times \prod_{j = 1}^{n} \sum_{g_{j}} T (g_{j} | g_{f}, g_{m}) f (y_{j} {| y_{f}, g_{f}, y_{m}, g_{m}, g}_{j})

where, each summation is over all the genotypes of that individual at the two loci, in its general form with un observed genotypes at both loci, and T_{(gj |gf , gm)} is the transmission probability for the case of unknown phase. In model (1) the conditional densities f (y_f |g_f), f (y_m|y_f, g_f, g_m) and f (y_j |y_f, g_f, y_m, g_m, g_j) can be any general densities. Latter on for easy of exposition and convenience of application, we will assume that f_{(yf |gf)} is the d-dimensional normal density with mean

μ_{f} = \sum_{i = 1}^{9} β_{i} χ (g_{f} = i) + β x_{f}

and variance matrix Σ_f, where the Χ(g_f = i) denote the event that the father's composite genotype if of type i, β's are d-dimensional vector of parameters and x_f is the covariates matrix for the father; in the same manner, f_{(ym|yf , gf , gm)} is the conditional normal density with mean

μ_{m} + Ω_{p} \sum_{f}^{- 1} (y_{f} - μ_{f})

where

μ_{m} = \sum_{i = 1}^{9} β_{i} χ (g_{m} = i) + β x_{m}

and variance matrix $Σ_{m} - Ω_{p} Σ_{f}^{- 1} Ω_{p}$ and Σ_m is the variance matrix of mother alone and Ω_p is the between-parents correlation matrix. Furthermore, we take K_{(g_f,g_m)} as the K-function as in Yuan and Bonney [10] which is an adjustment factor for the product of the penetrance of the sibs given the parents genotypes and f_{(yj|yf, gf, ym, gm, gj)} is the conditional normal density function with mean

μ_{j} + Ω_{s p} \sum_{p}^{- 1} (y_{p} - μ_{p})

where Ω_sp=(Ω_sf,Ω_sm) is the sib-parents correlation matrix which is composed of the sib-father and sib-mother blocks of correlation matrices,

\sum_{p} = (\begin{matrix} Σ_{f} & Ω_{p} \\ Ω_{p} & Σ_{m} \end{matrix}), y_{p} = (\begin{matrix} y_{f} \\ y_{m} \end{matrix}), μ_{p} = (\begin{matrix} μ_{f} \\ μ_{m} \end{matrix})

and variance matrix $Σ_{s} - Ω_{s p} Σ_{p}^{- 1} Ω_{s p}$ . Note that although we use the same coding for the two loci, but f₁=0 and f₂=0 do not mean the same gene at the two loci. The specification of the joint genotype proportion p_ij's and the transmission probabilities T_{(gj|gf, gm)} is put expression (10) latter, and its values are given in Table II.

Note in model (1), typically there are many zero components of the transmission probability T_{(gj|gf, gm)}, so that it will be more efficient to evaluate T_{(gj|gf, gm)} first, if its non-zero then compute the penetrances for the family members, otherwise ignore the computation for that combination of genotypes. The T_{(gj|gf, gm)}'s are functions of the recombination fraction r. When the phase is known, (1) should be modified as

L (y) = \sum_{g_{f}} P (g_{f}) f (y_{f} | g_{f}) \sum_{g_{m}} P (g_{m}) f (y_{m} | y_{f}, g_{f}, g_{m}) K (g_{f}, g_{m})

\times \prod_{j = 1}^{n} \sum_{g_{j}} T_{1} (g_{j} | g_{f}, g_{m}; h (g_{j}, g_{f}, g_{m})) f (y_{j} | y_{f}, g_{f}, y_{m}, g_{m}, g_{j}) (2)

where T_{1(gj|gf,gm; h(gj,gf,gm))} is the transmission probability for the give phase configuration h_{(gj, gf, gm)} of (gj|gf, gm). So (1) is can be rewritten as

L (y) = \sum_{g_{f}} P (g_{f}) f (y_{f} | g_{f}) \sum_{g_{m}} P (g_{m}) f (y_{m} | y_{f}, g_{f}, g_{m}) K (g_{f}, g_{m})

\times \sum_{h (g_{j}, g_{f}, g_{m})} P (h (g_{j}, g_{f}, g_{m})) \prod_{j = 1}^{n} \sum_{g_{j}} T_{1} (g_{j} | g_{f}, g_{m}, h (g_{j}, g_{f}, g_{m})) f (y_{j} | y_{f}, g_{f}, y_{m}, g_{m}, g_{j})

where Σ_h(gj,gf,gm) is summation across all different phase configurations h_{(gj, gf, gm)}s of (gj, gf, gm), and ?(h(_{gj, gf, gm})) is the probability of configuration h_{(gj, gf, gm)}. The number of different phase configurations of (gj, gf, gm) depends on the number of heterozygote's in it. Note here we have two loci, each locus has two genotypes, and the genotypes of the parents are assumed independent, as common in the literature. If there are k (0 ≤ k ≤ 6) heterogygotes in (gj, gf, gm), then there are 2k different phase configurations, and each has probability P (h_{(gj, gf, gm)})=1/2k. This method needs to enlist all the different phase configurations, since different triple (gj, gf, gm) may have different number of phase configurations, this method will not be easy in terms of programming. A more convenient way in programming is to treat each genotype as heterozygote, and sum over all the 26=64 phase configurations each with probability 1/64. Although this way will have some redundant computations, but is a general procedure, it does not require to enlist the phase configurations for each triple (gj, gf, gm), and so is easy to programming. The values of T_{(gj|gf, gm)} are given in Table II in the Appendix, for all possible composite genotypes of (gj, gf, gm). This is a general procedure for programming without the knowledge of the phase configuration for each triple.

Linkage between trait loci

For simplicity, we only consider the case of two phenotypes controlled by their own loci with unobserved genotypes at both loci.

Linkage between trait and marker loci

Suppose the data y is controlled by one locus with unobserved genotype, and we have the genotype g₂ of y at the marker locus, a common assumption is that, g₂ has no epistatic interaction with y, i.e. g and y has no direct connection, but g2 has relationship with the unobserved genotype of y, and phase unknown. In this case (1) becomes

L (y) = \sum_{g_{f 1}} P (g_{f}) f (y_{f} | g_{f}) \sum_{g_{m 1}} P (g_{m}) f (y_{m} | y_{f}, g_{f}, g_{m}) K (g_{f 1}, g_{m 1})

\times \prod_{j = 1}^{n} \sum_{g_{f 1}} T (g_{j} | g_{f}, g_{m}) f (y_{j} | y_{f}, g_{f}, y_{m}, g_{m}, g_{j}) (3)

here the summation is only for all the genotypes at the trait locus.

Point analysis

One way of multi-point linkage analysis is to perform 3-point analysis step by step across the segment span the multipoint. Here we use our model to address the 3-point analysis. In this problem, we have two markers and an unknown disease locus, which may lie between the two markers or outside the interval between them. We assume that the case is unknown, while the model is similar when the phase is known. Again, we only need to specify the likelihood for one family. The composite genotypes are g_f = (g_f1, g_f2, g_f3) for the father, gm= (gm1, gm2, gm3) for the mother, and gj= (gj1, gj2, gj3) for the j-th sib. We assume the first and second genotypes in the composite genotype of each individual are the observed genotypes at markers 1 and 2, the third marker gj3 is the unobserved disease genotype, assuming marker g_j1 is located at the left side of marker g_j2 on the chromosome. Since we have three loci, there are three recombination fractions for the three pair wise loci. Denote r₁ as the recombination fraction between marker 1 and the disease marker, r₂ as that between marker 2 and the disease, r3 as that between the first two markers, and T(g_j1, g_j2, g_j3|g_f1, g_f2, g_f3); (g_m1, g_m2, g_m3)) the 3-point transmission probability, which is a function of (r₁, r₂, r₃). In this case, (3) is rewritten as

Appendix A:

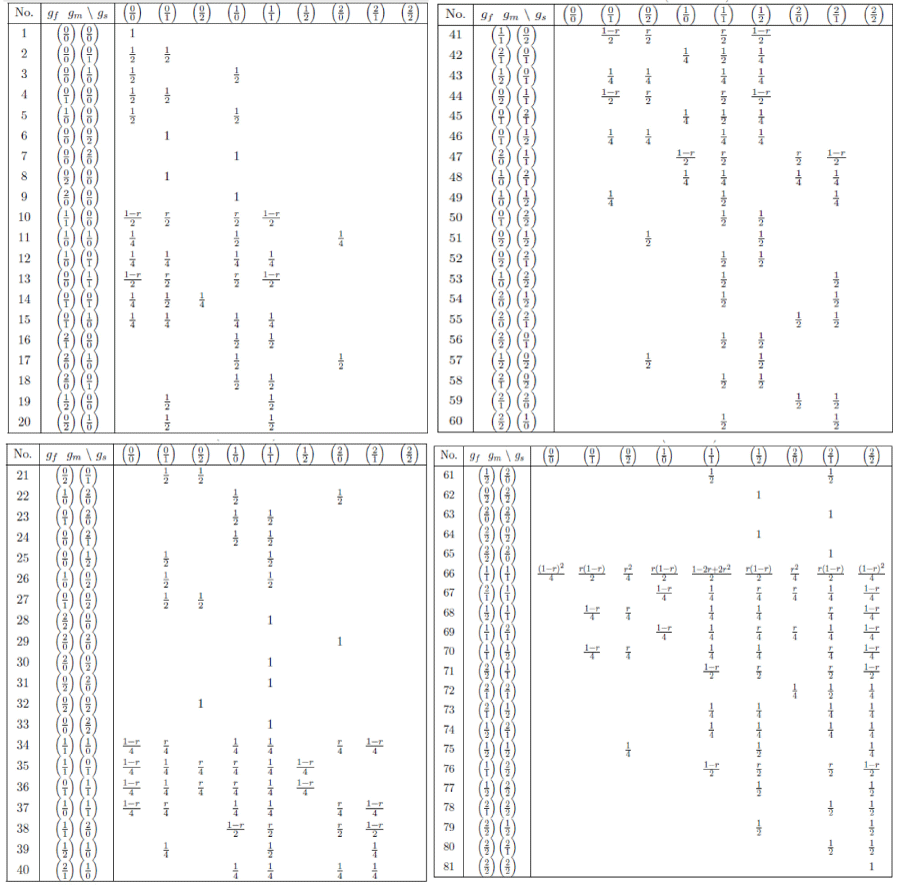
Appendix A

    
    
    Appendix A

L (y) = \sum_{g_{f_{3}}} P (g_{f}) f (y_{f} | g_{f}) \sum_{g_{m_{3}}} P (g_{m}) f (y_{m} | y_{f}, g_{f}, g_{m}) K (g_{f_{3}}, g_{m_{3}})

\times \prod_{j = 1}^{n} \sum_{g_{j_{3}}} T (g_{j_{1}}, g_{j_{2}}, g_{j_{3}} | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) f (y_{j} | y_{f}, g_{f}, y_{m}, g_{m}, g_{j}) (4)

Note in this model, although f (.|.) has the same form as in model (1), but the mean μ's has 27 coefficients for all the possible different 3-point composite genotypes, instead of 9. In equation (4) the key is the specification of the 3-point transmission probability. Note that the three recombination fractions are not independent. During meiosis, when there is a cross-over at marker 1, and no cross-over at the other two loci, then there is a recombination event between marker 1 and the disease marker, it is also a recombination event between marker 1 and marker 2; however if there is also a cross-over at marker 2, then there is no recombination event between marker 1 and marker 2. If we consider all the possibilities of crossovers at the 3 markers, the relationships of r₁, r₂ and r₃, and the combinatory outcomes of the 3-point gametes can be complicated. In this case a complete Table of all the 3-poin transmission probabilities as in Table II will have 729x27 entries. So it is impractical to list all such probabilities. One may use Haldane's model (Lange 1997, p110) for the specification, but this model is not easy to implement into software. Observe that

T (g_{j_{1}}, g_{j_{2}}, g_{j_{3}} | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) = \frac{P (g_{j_{1}}, g_{j_{2}}, g_{j_{3}}; g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}})}{P (g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}})}

= \frac{P (g_{j_{1}}, g_{j_{2}} | g_{j_{3}}; g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) P (g_{j_{3}}; | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}})}{P (g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}})}

= P (g_{j_{1}}, g_{j_{2}} | g_{j_{3}}; g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) P (g_{j_{3}}; | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}})

= P (g_{j_{1}}, g_{j_{2}} | g_{f_{1}}, g_{f_{2}}; g_{m_{1}}, g_{m_{2}}) P (g_{j_{3}} | g_{f_{3}}; g_{m_{3}}) = T_{3} (g_{j_{1}}, g_{j_{2}} | g_{f_{1}}, g_{f_{2}}; g_{m_{1}}, g_{m_{2}}) P (g_{j_{3}} | g_{f_{3}}, g_{m_{3}})

Similarly,

T (g_{j_{1}}, g_{j_{2}}, g_{j_{3}} | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) = T_{2} (g_{j_{2}}, g_{j_{3}} | g_{f_{2}}, g_{f_{3}}; g_{m_{2}}, g_{m_{3}}) P (g_{j_{1}} | g_{f_{1}}, g_{m_{1}})

and

T (g_{j_{1}}, g_{j_{2}}, g_{j_{3}} | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) = T_{1} (g_{j_{1}}, g_{j_{3}} | g_{f_{1}}, g_{f_{3}}; g_{m_{1}}, g_{m_{3}}) P (g_{j_{2}} | g_{f_{2}}, g_{m_{2}})

Where Ti (•|•) is a function of ri and its values are given in Table II, just replace r there by r_i (i = 1, 2, 3). The values of P (g_j|g_f, g_m) are given in Table III for convenience. So we specify the 3-point transmission probability as

T (g_{j_{1}}, g_{j_{2}}, g_{j_{3}} | g_{f_{1}}, g_{f_{2}}, g_{f_{3}}; g_{m_{1}}, g_{m_{2}}, g_{m_{3}}) = \frac{1}{3} (T_{1} (g_{j_{1}}, g_{j_{3}} | g_{f_{1}}, g_{f_{3}}; g_{m_{1}}, g_{m_{3}}) P (g_{j_{2}} | g_{f_{2}}, g_{m_{2}})

+ T_{2} (g_{j_{2}}, g_{j_{3}} | g_{f_{2}}, g_{f_{3}}; g_{m_{2}}, g_{m_{3}}) P (g_{j_{1}} | g_{f_{1}}, g_{m_{1}}) + T_{3} (g_{j_{1}}, g_{j_{2}} | g_{f_{1}}, g_{f_{2}}; g_{m_{1}}, g_{m_{2}}) P (g_{j_{3}} | g_{f_{3}}, g_{m_{3}}))

Finally, the MLE (r^₁, r^₂, r^₃) of (r₁, r₂, r₃) is computed. If r^₁ = max {r^₁, r^₂, r^₃}, the disease locus is more likely lies on the right side of marker 2; if r^₂ = max {r^₁, r^₂, r^₃}, the disease locus is more likely lies on the left side of marker 1; If r^₃ = max {r^₁, r^₂, r^₃}, the disease locus is more likely lies between markers 1 and 2.

Multi-point analysis

In genome wide linkage analysis, there are often hundreds of markers to be considered. Instead one marker at a time, it is known that analyzing all the makers together will enhance the power. Let k be the total number of markers under consideration, there are k (k - 1)/2 pair wise recombination's fractions r_ijs. It is difficult to estimated all the recombination's in a model, and it is unnecessary, but usually the map distances of the markers are known, so the recombination fractions among the markers can be estimated automatically using map functions, for example the Hadane function or Kosamby function. If we know actually all the particular marker positions on the chromosome, their recombination's fractions then can be determined. So if we let r_0j be the recombination fraction between the disease locus and the locus of marker j, which are the only unknown recombination fractions to be estimated, we assume that the other r_ijs (i, j ? 0) are known. As far as we know, usually the markers are from haplotype blocks, different blocks are weakly dependent, and the markers within the same block are strongly dependent, but not perfectly dependent. For some blocks, only one marker is typed, while in some other blocks there are more than one marker. Then a likelihood using all the traits as in equation (4) will be impractical as it will involve too many parameters. Instead, we may consider the likelihood only use the observed marker composite genotypes. Let r = (r_01,...,r_0k), (g_f0, g_m0, g_j0) be the unobserved genotypes of (father, mother, sib), g_f= (g_f0, g_f1,...,g_fk) be the composite genotype of the father, g_m = (g_m0, g_m1, ...,g_mk) be that of the mother, and g_j = (g_j0, g_j1,...,g_jk) be that of the j-th sib. The likelihood for one family is

Table 1: Linkage Results on chromosome 4 for ntth1.




  
    SNP 
    Marker Name
    Map Distance(cM)
    Allele 
    Lodscore
  
  
    84
    tsc1276837
    34.24 
    2 
    1.75 
  
  
    146
    tsc0526379
    52.99 
    1 
    1.92 
  
  
    148
    tsc0045058
    53.26 
    1 
    3.35 
  
  
    159
    tsc0527513
    55.57 
    2 
    1.93 
  
  
    295
    tsc1213381
    85.42 
    2 
    2.22 
  
  
    319
    tsc0055068
    89.31 
    2 
    3.03 
  
  
    714
    tsc0051777
    172.86 
    2 
    2.57



Table 1:  Linkage Results on chromosome 4 for ntth1.

L (r) = \sum_{g_{f_{0}}} P (g_{f}) \sum_{g_{m_{0}}} P (g_{m}) \prod_{j = 1}^{n} \sum_{g_{j_{0}}} T (g_{j} | g_{f}, g_{m}) (5)

Then the problems are how to specify P (g_f) and how to specify T (g_j|g_f, g_m)? For the transmission probability, Haldane's model (Lange [11]) is not easy to use, since it requires the recombination status among the markers, which are always unknown with the phases. Let T_rs = T_rs (g_jr, g_js|g_fr, g_fs; g_mr, g_ms) be the transmission probability at marker loci (r, s), we can specify the transmission as in the three point case, as

T (g_{j} | g_{f}, g_{m}) = \frac{1}{k} {\begin{matrix} T_{0, 1} T_{2, 3} T_{4, 5} ... T_{k - 1, k} + T_{0, 2} T_{1, 3} T_{4, 5} ... T_{k - 1, k} + ... + T_{0, k} T_{1, 2} T_{3, 4} ... T_{k - 2, k - 1}; \\ T_{0, 1} T_{2, 3} T_{4, 5} ... T_{k - 2, k - 1} P (g_{j_{k}} | g_{f_{k}}, g_{m_{k}}) + T_{0, 2} T_{1, 3} T_{4, 5} ... T_{k - 2, k - 1} P (g_{j_{k}} | g_{f_{k}}, g_{m_{k}}) \end{matrix}

{\begin{matrix} i f \begin{array}{r}  \end{array} k = 2 l - 1; \\ \begin{array}{r} + ... + T_{0, k} T_{1, 2} T_{3, 4} ... T_{k - 3, k - 2} P (g_{j_{k - 1}} | g_{f_{k - 1}}, g_{m_{k - 1}}); & \begin{array}{r} i f & k = 2 l . \end{array} \end{array} \end{matrix} ()

For r ? 0, the T_r,s 's are given in Table II, with r replaced by r_rs; P (g_j|g_f, g_m) is the corresponding one-locus transmission probability at the unpaired left-over locus. Once P (g_f) (and so P (g_f)) is specified, T (g_j|g_f, g_m) in equation (6) is a quadratic function of r. It can be applied to any nuclear family design.

The method in Liang et al.[12] is also simple, but it requires to known the trans- mitted allele status of father and mother at each loci, which are sometimes uncertain, or can only be inferred with 1/2 probability. Also this method applies to only to the case-parent trio design.

Specification of the haplotype and the transmission probabilities

Specification of the haplotype probability: A simple way is to assume linkage equilibrium between the two loci and set

P(g)=P(g1)P(g2)      (7)

However this assumption is inappropriate with the presence of linkage [13-15]. When dealing with Linkage Disequilibrium (LD), we usually need to consider all possible gametic disequilibrium within the haplotype [16], which will be very complicated for three or more alleles. With model (1) and (2), we can define the LD parameter as

δ = P (g) - P (g 1) P (g 2) (8)

In case of Hardy-Weinberg Disequilibrium (HWD), let f be the common HWD parameter [17,18] at the two loci, at each locus

p_{k k} : = P (A_{k} A_{k}) = p_{k}^{2} + p_{k} (1 | - p_{k}) f, p_{k l} : = P (A_{k} A_{l}) = p_{k} p_{l} (1 - f), k \neq l,

we have

P (g) = p_{i j}^{1} p_{k l}^{2} + δ (9)

Where $p_{i j}^{1} = P (a_{i} a_{j})$ is the genotype probability at the trait locus and $p_{k j}^{2} = P (A_{k} A_{l})$ is the probability at the marker, and both of them satisfy the above HWD specification.

Specification of the transmission probability: Let r be recombinant fraction - the probability that a given sib's genotype is a recombinant of those of his/her parents'. 0 ≤ r ≤ 1/2, r = 0 corresponds to complete linkage of the two loci, r = 1/2 corresponds to no linkage (Sham [19]). For the two-allele two loci case, there are 3⁶ = 729 possible values of T (g_s|g_f, g_m), but only a few different ones and many zeros. If the genotypes are ordered, let g_s = g_sf||g_sm, where g_sf be the paternal gamete and g_sm the maternal gamete, we have (Lange 1997).

T (g_{s} | g_{f}, g_{m}) = T (g_{s f} | g_{f}) T (g_{s m} | g_{m}) .

Given $g_{f} = (\frac{a ‖ b}{A ‖ B})$ we list all the non-zero values of $T (\cdot | (\frac{a ‖ b}{A ‖ B}))$ , with various settings of g_sf, as the following

T (\cdot | (\frac{a ‖ b}{A ‖ B})) = {\begin{array}{r} (\frac{a}{A}), & \begin{array}{r} \begin{matrix} a = b & & A = B; \end{matrix} \end{array} \\ 1 \\ (\frac{a}{A}) & (\frac{b}{A}), \begin{matrix} a \neq b & & A = B; \end{matrix} \\ \frac{1}{2} & \frac{1}{2} \\ (\frac{a}{A}) & (\frac{a}{B}), \begin{matrix} a = b & & A \neq B; \end{matrix} \\ \frac{1}{2} & \frac{1}{2} \\ (\frac{a}{A}) & \begin{matrix} (\frac{b}{B}) & (\frac{a}{B}) & (\frac{b}{A}), \begin{matrix} a \neq b & & A \neq B; \end{matrix} \end{matrix} \\ \frac{1 - r}{2} & \begin{matrix} \frac{1 - r}{2} & \frac{r}{2} & \frac{r}{2} \end{matrix} \end{array} (10)

the values of T (g_sm|g_m) are the same.

Using (10) and the product T (g_sf|g_f) T (g_sm|g_m) we can get all the transmission probabilities in allelic representation for each sib genotype g_sf|g_sm.

We list all the non-zero values of the transmission probabilities in numerical notation in Table II in Appendix A. All the 81 combinations of parent's genotypes are given in the second column, all those 9 for the sib given in the first row. An illustration of the computation of the entries in the table using (10) or directly by hand is given in the Appendix B.

Table II: (f_m, leptin) = (X_g, sex, age).




  
    ? 
     
     
  
  
    �_0,1 
    11.682(2.855) 
    11.659(2.904) 
  
  
    �_0,2 
    -2.146(0.464) 
    -2.292(0.464) 
  
  
    a_1,1
    2.527(0.574) 
    2.591(0.480) 
  
  
    a_2,1
    1.430(0.670) 
    1.639(0.550) 
  
  
    �_2,1
    12.929(1.024) 
    12.913(1.024) 
  
  
    �_2,2
    19.558(1.192) 
    19.531(1.192) 
  
  
    �_3,1 
    0.211(0.032) 
    0.210(0.032) 
  
  
    �_3,2
    0.202(0.037) 
    0.202(0.037) 
  
  
     
    212.630(12.225) 
    212.575(12.245) 
  
  
     
    289.787(16.109) 
    289.785(16.132) 
  
  
    ?_w
    0.636(0.023) 
    0.636(0.023) 
  
  
    ?_b[1,1]
    0.262(0.047) 
    0.262(0.047) 
  
  
    ?_b[1,2]
    0.242(0.038) 
    0.242(0.038) 
  
  
    ?_b[2,2]
    0.264(0.042) 
    0.264(0.042) 
  
  
    qA₁
    0.736(0.313) 
    0.738(0.325) 
  
  
    qA₂
    0.757(0.609) 
    0.753(0.610) 
  
  
    r
    0.500 
    0.000 
  
  
    loglike 
    -4505.583996 
    -4505.559749



Table II:  (f_m, leptin) = (X_g, sex, age).

Application

We analyze the data set released by the Gegetic Analysis Workshop14 using the pro- posed method. Recently, evidence has been found to relate alcoholism to genetic factors [20-22]. The Collaborative Study on the Genetics of Alcoholism (COGA) is a program to study this phenomenon extensively. The data set contains multiple phenotypes and genome wide scans from 229 families and 1490 individuals, in which 720 of them have incomplete/missing observations. Each individual has 20 records, among which the first 5 are i.d. or categorical, most of the other variables are continuous traits, including fat mass (fm) and leptin. We break the data into nuclear families. Sibs with missing response(s)/covariate(s) are deleted from the data, parents with missing response(s)/covariate(s) are kept in order for tracking down the family structure.

We first study the genetic association of electrophysiological measures related to alcoholism focusing on the NTTH phenotypes and the 786 Affymetrix SNPs on chromo- some 4. This chromosome has been shown to be involved in NTTH phenotypes in some previous studies.

There are four NTTH quantitative phenotypes: ntth1, ntth2, ntth3 and ntth4. Typically for this problem, one may perform a linkage analysis to pinpoint the highly spurious region, but this is computationally intensive and time consuming. In this dataset, the number of SNPs is large. For chromosome 4 alone there are 786 SNPs. We did a two- stage analysis. The first stage is an association analysis, in which we regressed the trait on age, sex, and the SNPs, one at a time, across all the 786 SNPs on chromosome 4. This will analyze the statistical association between the phenotypes and the SNPs, which will provide us the phenotypes/SNPs with significant association for the next stage analysis. In the second stage, a formal linkage analysis was performed using model (1) on the SNPs selected from the first stage. After the two-stage analysis, we found ntth1 has strong linkage to some SNPs, while the trait linkage for ntth2-httn4 is not significant. The results on ntth1 for those SNPs with significant linkage are presented in Table I.

From this table, we find strong linkage in four regions: SNPs tsc0045058, tsc1213381, tsc0055068 and tsc0051777 at chromosome positions 148, 295, 319 and 714, with map distances 53.26, 85.42, 89.31 and 172.86cM; and moderate linkage in three regions: tsc1276837, tsc0526379 and tsc0527513 at positions 84, 146 and 159, with map distances 34.24, 52.99 and 55.57 cM.

Next we test the hypothesis of no linkage between the loci and the trait. It is known that fat mass and leptin are closely related phenotypically, we are interested in the genotypic relationship between them, and assume they are controlled by their own gene loci, with sex and age as covariates. Without genotype data at both loci, the parameters of interest include the effects of the covariates, the unobserved genotypes, of their allele proportions and the recombination fraction between the two loci. Let ? be the vector of all the parameters in the model, ?ˆ be its M.L.E. from the mixture model. Consider the application of model (1) with the haplotype probability given by (5). Let H0 be the hypothesis that there is no linkage between the two trait loci, i.e. H0: r = 0.5. The results are shown in Table 2 below, where ?ˆ and ?ˆ0 are the m.l.e. of ? under the full model and H0 respectively (in brackets are the estimated standard deviations). In this case the hull hypothesis is r = 0.5 lies on the boundary of the parameter, instead of the standard likelihood ratio test, the 2 times log-likelihood ratio statistic in this case is asymptotically a 0.5:0.5 mixture of $χ_{0}^{2} and χ_{1}^{2}$

[Self and Liang, 1987], which in our case is 0.485 with an approximate P-value of 0.2. Thus the hypothesis H0 of no genetic linkage between fat mass and leptin is rejected at a high significance level (Table 2).

-2 log-likelihood ratio = 0.48494, with a P-value≈0.2 under the 0.5:0.5 mixture of $χ_{0}^{2} and χ_{1}^{2}$

Discussion

We have considered a simple likelihood model to study linkage between traits and between trait and marker loci, without requiring IBD data as most linkage studies do, thus makes it easy to use for both the quantitative and qualitative traits. The hypothesis of no linkage can be tested by the standard likelihood ratio under this model. The model is applicable to pedigree, nuclear family or sib pairs, along with segregation and regressive analysis. Using this model to the GWA14 data, we find strong genetic linkage between ntth1 at some SNP loci.

The usual linkage analysis is based on the assumption of linkage equilibrium between loci, which is inappropriate. Some other approaches with combined linkage and linkage disequilibrium [4,15,23], this will yield more information. The disequilibrium may be specified as in (7) or some other measures as reviewed by Devlin and Risch [24]. But LD may be affected by many factors, such as mutation, drift, selection, population stratification or admixture, etc., which create difficulties in LD analysis. Our method can also be extended to this case along with Hardy-Weinberg disequilibrium, as in Wright [17] and Cockerham [18] and to different likelihood formulations, or even to semi-parametric and nonparametric models. We can also incorporate the multipoint marker information into the model to increase its power. Although we only presented the model for the two-allele case at each locus, this model cab be extended to multiple allele case, while the corresponding transmission matrix to that in Appendix A will be a real challenge. For two loci with k₁ and k₂ alleles each, one needs to compute a (n₁n₂)² x n₁n₂ transmission matrix, where n_i = k_i (k_i + 1)/2 is the number of genotypes at the i-th locus. This can be partially resolved by a stepwise procedure; we can cut the loci to two alleles at each step, and then select the sections with stronger linkage for next step.

There is a trade-off between the effectiveness and robustness of methods. The non- parametric and semi-parametric models are in general robust since they require no or little model assumptions, but they may suffer from potential loss of efficiency by the same reason.

References

Download PDF

Citation: Yuan A, Zhong X and Bonney GE. A Likelihood Model for Linkage Analysis of Genetic Traits. Austin Biom and Biostat. 2014;1(1): 7. ISSN: 2378-9840

Instruction for Authors

Submit Your Article