
Research Article
Austin Biom and Biostat. 2015;2(1): 1014.
Refining Evaluation Methodology on TNM Stage System: Assessment on HPV-Related Oropharyngeal Cancer
Xu W1,2*, Shen XW1, Su J¹, O’Sullivan B3,4 and Huang SH³
¹Department of Biostatistics, Princess Margaret Cancer Center, Canada
²Dalla Lana School of Public Health, University of Toronto, Canada
³Department of Radiation Oncology, Princess Margaret Cancer Centre, Canada
4Ontario Cancer Institute, University Health Network, Canada
*Corresponding author: Xu W, Department of Biostatistics, Princess Margaret Cancer Center, Dalla Lana School of Public Health, University of Toronto, 10-512, 610 University Ave, Toronto, ON M5G 2M9, Canada.
Received: March 16, 2015; Accepted: March 27, 2015; Published: April 08, 2015
Abstract
TNM stage is important in treatment decision-making and outcome predicting. The existing Oropharyngeal Cancer (OPC) TNM stages have not made distinction of the two sub sites of HPV+ and HPV- diseases. Besides that, the current TNM stage grouping is generally derived based on literature review and clinical understanding of the disease processes. It is important to have quantitative assessment on the prognostic ability and stability of the TNM stage on HPV-related OPC patients. The current stage evaluation criteria use non-parametric methods and assess the stage performance on limited time points. Even though the current stage systems were mostly developed based on retrospective data, these evaluation criteria don’t consider the important clinical confounders. We developed novel criteria to assess performance of the TNM stage grouping schemes based on parametric modeling adjusting on important clinical factors. These criteria evaluate the TNM stage grouping scheme in five different measures: hazard consistency, hazard discrimination, explained variation, likelihood difference, and balance. The novel criteria were applied to evaluate newly developed TNM stage grouping schemes on HPV+ OPC patients and a few existing TNM stage grouping schemes. The new HPV+ OPC TNM stage outperforms all existing schemes on prognosis and stability.
Keywords: TNM stages; Evaluation criteria; Parametric model; Head and Neck Cancer; Prognosis
Introduction and Background
T (extent of the primary tumor), N (absence or presence and extent of regional lymph node metastasis) and M (absence or presence of distant metastasis) are three components to describe the anatomical tumor extent. In clinic, the TNM categories are combined to classify patients into stage groups with similar survival performance. TNM staging system plays an important role in treatment decision-making and outcome predicting. The most widely used TNM stage grouping scheme is proposed by the Union of International Cancer Control (UICC) and American Joint Committee on Cancer (AJCC) [1].
The TNM staging system is revised periodically to reflect changes in outcomes (generally based on overall survival) as a result of better defining anatomic disease extent from new imaging modalities, improved therapeutic efficacy, and increasing knowledge about tumor biology. The performance of any new staging on outcome prediction should be evaluated objectively.
The commonly used evaluation criteria for TNM stage grouping is proposed by Groome et al. [2] including hazard consistency, hazard discrimination, outcome prediction, and balance. However, most of the current TNM stage systems were developed based on retrospective data; these evaluation criteria don’t consider the potential clinical confounders, especially treatment, that may strongly affect the survival outcomes. Ignoring the important clinical factors in the development and evaluation of stage grouping systems may lower the accuracy of distinguishing risk groups [3]. Furthermore, the existing criteria use non-parametric methods to evaluation hazard consistency and hazard discrimination based on limited time points (monthly rate over 5 years). The use of complete time to event information is needed for the performance evaluation to improve efficiency and accuracy.
We introduced new criteria to assess performance of the TNM stage grouping schemes based on parametric modeling adjusting for important clinical factors, using HPV-driven (HPV+) Oropharyngeal Cancer (OPC), as an example. HPV+ OPC, a fast emerging disease entity, is different from traditional smoking/alcohol related OPC in many ways. Many studies have shown that HPV+ OPC patients tend to have better survival and lower recurrence rates compared to HPV- OPC patients [4-6]. Currently for OPC, UICC/AJCC stage grouping scheme has not made distinction of these two diseases and is derived from the historical data that are comprised of mainly HPVOPC patients. Other existing stage grouping schemes were proposed to improve the prognostic ability of UICC/AJCC, but still paying little attention on the distinction between HPV+ and HPV- OPC patients [7-12]. Takes et al. [13] discussed about the shortcomings of the current TNM classification system (UICC/AJCC) within head and neck cancer and suggested to improve and expand current TNM system based on tumor, patient and environment-related factors.
In the present study, we firstly applied Recursive Partitioning Analysis (RPA) model in non-metastatic HPV+ OPC patients treated in our institution to derive a new stage grouping scheme using the same TNM classification. Then, we applied both the current and the new criteria on the newly developed TNM stage grouping scheme and a few existing TNM stage grouping schemes including UICC/ AJCC 7th edition [14], TANIS, Synderman, Hart, Berg, Kiricuta, and Hall [7-12]. We also evaluated the performance of the new criteria using bootstrap algorithm and multiple imputations as validation.
Methods
Refined TNM stage grouping for HPV+ OPC
After institutional Ethic Board approval, a retrospective review was conducted for 573 newly diagnosed p16 confirmed HPV+ OPC treated in our institution during January 2000 to December 2010. Patients whose p16 status was unknown or who had metastatic disease at presentation were excluded. T- and N-classification was based on UICC/AJCC TNM 7th edition for OPC [1,15]. Median follow up was 3.82 years.
To derive new TNM stage groupings for HPV+ OPC, RPA method was explored using Overall Survival (OS) as outcome endpoint. A new stage scheme was derived using ordinal T- (T1/T2/ T3/T4) and N- (N0/N1/N2a/N2b/N2c/N3) categories objectively. The RPA algorithm is based on the optimized binary partition of T or N categories. It results in subgroups with relatively homogeneous survival performance. The derived stages were termed RPA-stages [16]. The performance of the newly derived TNM stage grouping schemes is evaluated against the following existing TNM stage grouping schemes which were developed for head and neck cancers:
UICC/AJCC 7th edition: It was derived based on clinical understanding of the disease processes, with an interest in maintaining the same scheme across as many head and neck cancer sites as possible. It has been widely used in most head and neck cancer sites now.
The TANIS scheme: It was proposed by Jones et al. [7] as an easyto- remember approach. It was developed based on the observations that, in head and neck cancers, the corresponding T and N categories yield similar prognostic effects and that those effects were linear, thereby allowing the T and N integers to be summed and generating the TANIS-7 scheme. The investigators showed that three TANIS groupings (TANIS-3): 1-3, 4, and 5-7 discriminated better than UICC/AJCC in their study population.
The snyderman scheme: Snyderman and Wagner [8] derived another staging scheme from the TANIS scheme by identifying optimal groupings based on visual examination of the TANIS survival curves. They derived the scheme based on a population consisted of 186 cases of oral cavity carcinoma treated with primary surgery and they used disease-free survival as primary outcome of interest.
Hart scheme: Hart et al. [9] developed a scheme from an analysis of disease-specific survival in 640 OPC cases. A stepwise backward elimination model was applied to determine stage groupings.
Kiricuta scheme: Kiricuta [10] later introduced a scheme with some modification to the one proposed by Hart.
Berg scheme: The scheme proposed by Berg [11] was based on observed survival rates and compared with UICC/AJCC by assessing the degree of discrimination among survival curves.
Hall scheme: Groome and Hall [12] proposed a scheme, which further separated N2 category into N2a and N2bc in the design of the stage grouping.
We compared the TNM stage group schemes of UICC/AJCC 7th edition, TANIS, Synderman, Hart, Kiricuta, Berg, Hall, and the newly derived stage grouping schemes (RPA-staging scheme). An overview of the T and N category combinations and distributions within each of these schemes is provided on Figure 1. We refer to a subgroup as the patients with a specific combination of T and N categories and group as the combination of subgroups within a stage grouping scheme. The terms classification, scheme and system are used interchangeably.
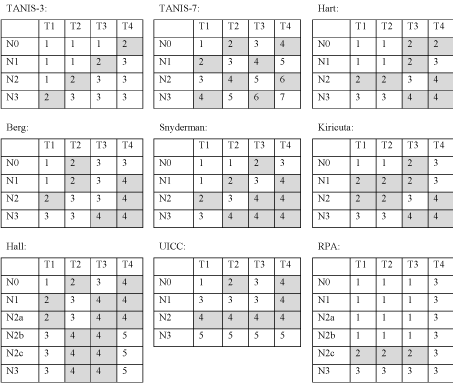
Figure 1: Schematic showing stage grouping schemes.
Existing criteria for evaluation of schemes
Groome et al. [2] proposed four criteria to evaluate prognostic ability of existing stage grouping schemes. “Hazard Consistency” addresses the issue of the homogeneity of the patients within each subgroup for all stage groups. They calculated a weighted average of the survival difference between each stage grouping for a given scheme and the subgroups that make up that grouping, where the weights were based on the amount of person time contributed by the subgroups (Equation 1).
(1)
In Equation 1, ptti refers to the person time at time ti for the whole population, while ptg,ti refers to the person time at time ti for the subgroup g. sg,ti refers to the survival probability at time ti for the subgroup g, while sg,ti refers to the survival probability at time ti for stage group G, where the subgroup g belongs to the stage group G. Monthly time points over five years were used in this calculation, and there were 20 subgroups in total (combination of T1/T2/T3/T4, and N0/N1/N2a/N2bc/N3). This measure can be directly interpreted as the average survival rate difference between the subgroups and the groups for a given staging scheme. Lower scores indicate better consistency between subgroups that make up the groups and groups themselves.
“Hazard Discrimination” addresses the question of the heterogeneity of patients between each adjacent stage group. It was measured by evaluating how evenly the group survival curves are spaced and how large a survival rate difference they span over the entire observation period (in this case, 60 months) (Equation 2).
(2)
Similar to the measurement of hazard consistency, monthly data of five years were used in this calculation and NG refers to the number of stage groups within a given scheme. The evenness of the survival curves was measured as the ratio of the product terms of the observed space between adjacent curves and the optimal spacing obtained when the curves are equidistant. The span of the survival curves was measured by accumulating the survival distances between the highest and lowest curves for a given scheme along time. Averaging these two measurements gives a summary score for hazard discrimination ranging from 0 to 1 with a higher score indicating better discrimination between survival curves.
“Outcome Prediction” was measured in two ways. First, the percent of the variance in the survival rates explained by each stage grouping scheme (PVE) was calculated using V2 previously defined by Schemper [17]. This approach allows the use of censored data to address cure prediction [2]. Second, the accuracy of the predictions of survival and death was estimated by “slope”, which was calculated by subtracting the mean probability of cure assigned to those who (in hindsight) were cured, from the mean probability of cure assigned to those who were not cured [18, 19]. This analysis assumes survival at 3 years captures all who were and were not cured. It used 3-year diseasefree survival probability as the surrogate for prediction of cure. This measurement requires non-censored follow-up, therefore patients who died of other causes within 3 years and those whose follow-up did not reach 3 years had to be excluded from the calculation. For both measurements, a higher score indicates better prediction power of the scheme.
“Balance” was quantified by computing the sum of the absolute differences between the observed proportions of cases in each group compared with the expected if an equal number of patients were in each (Equation 3).
(3)
In Equation 3, C refers to the number of total cases in the study population; while cG refers to the number of cases within stage group G. NG refers to the number of stage groups within a given scheme. This score expresses the average deviance from a balanced distribution of cases with a higher score indicating worse scheme.
The actual score for each criterion for each of the scheme was normalized and then summarized by using a weighted sum of the component scores, which puts equal weights on hazard consistency, hazard discrimination, PVE and slope, with less weight on balance as it is of more statistical than clinical relevance. Finally, stage grouping schemes were ranked based on the summary scores with the lowest summary score ranking first.
New evaluation criteria
Currently, the evaluation methodology proposed by Groome et al. [2] was acknowledged to be the standard for the testing and reporting of prognostic stage grouping schemes in head and neck oncology [20]. However, there are some limitations in this method. First, since current staging systems were mostly developed based on historical data, indicating that clinical factors, especially treatment, may strongly affect the survival outcome, the evaluation criteria should not ignore these potential clinical factors. With such consideration, we proposed new criteria for evaluating performance of current stage grouping schemes. We applied parametric approach to evaluate hazard consistency and hazard discrimination by using the likelihood ratio statistics from multivariate Cox proportional hazards regression model [21] with multiple adjusted clinical covariates. Second, the criterion of “outcome prediction” was evaluated in two different ways (Explained Variation and “Slope”) in Groome’s criteria. In the calculation of “slope”, patients who were censored or dead before 3 years follow-up were excluded from the analysis, which may introduce a bias in the evaluation of prediction power. In our new scheme, we used the percent of the variance in the survival rates explained by a given grouping scheme to evaluate the prediction ability. Furthermore, limited time points (monthly rate over 5 years) were used in both “Hazard Consistency” and “Hazard Discrimination” calculation. We proposed to use the complete follow up information for the evaluation.
Our new scheme was based on five evaluation criteria including hazard consistency, hazard discrimination, likelihood difference, explained variance, and balance. Preliminary analysis was conducted separately for HPV+ and HPV- cohort to determine key clinical predictors for overall survival.
Hazard consistency: We compared the log-likelihood statistic of the following two models:
(1) Cox proportional hazards model for overall survival, adjusted for significant clinical variables from preliminary analysis and an indicator variable for each of the 24 TN subgroups;
(2) Cox proportional hazards model for overall survival, adjusted for significant clinical variables from preliminary analysis and an indicator variable for each of the stage groups of a given scheme
Breslow’s method [22] (Equation 4) was used for the estimation of likelihood function since it is the most efficient method when there are no ties on event times. Likelihood ratio test was used to compare model (1) and (2). Asymptotically, the test statistic (-2 times the difference of log-likelihood of the two models) is distributed as a chi-squared random variable, with degrees of freedom equal to the difference in the number of parameters between the two models.
(4)
In Equation 4, t1 < t2 < … < tk denote the k distinct, ordered event times. Ri denote risk set just before the ith ordered event time ti. β is the vector of model parameters, while Zj(t) denote the vector of covariates for the jth individual at time t. di denote the number of event at time ti. Since there are no ties on event times for our dataset, di = 1 for all i, Equation 4 can be simplified to
Since different schemes may have different number of stage groups, the score of hazard consistency was then calculated by normalizing the likelihood ratio test statistic for each scheme (Equation 5), therefore allowing the direct comparison of schemes.
(5)
In Equation 5, L1 and L2 denote the likelihood of model 1 and 2 respectively. NG is the number of stage groups for the scheme. By normalizing the test statistic, the score of hazard consistency approximately follows a chi-square distribution with 1 degree of freedom. The score can be interpreted as how well can the stage groups represent subgroups, with a lower score indicating better hazard consistency.
Hazard discrimination: We compared the log-likelihood statistic of the following two models:
(2) Cox proportional hazard model for overall survival, adjusted for significant clinical variables from preliminary analysis and an indicator variable for each of the stage groups of a given scheme;
(3) Cox proportional hazard model for overall survival, adjusted for significant clinical variables from preliminary analysis and a continuous variable representing the stage groups for a given scheme
Similar to hazard consistency, Breslow’s estimation of likelihood was applied and likelihood ratio test was used to compare model (2) and (3). The score of hazard discrimination was then calculated by normalizing the likelihood ratio test statistic for each scheme (Equation 6).
(6)
A smaller score indicates a better linear trend in log hazard ratio from the lowest stage group to the highest stage group. We used this score to measure hazard discrimination since it is analogous to the first part of “hazard discrimination” score under the existing evaluation criteria, where the scheme with better hazard discrimination was expected to have evenly spaced survival curves.
Explained variation: The proportion of the variation of censored survival times explained by a given proportional hazards model was measured by V, which is proposed by Schemper and Henderson [23]. While the existing criteria used V2 [17] and did not adjusted for clinical factors [2,17]. In the recent PVE measurement, V has improved the handling of censoring and used mean absolute deviation between the predicted survival from Cox model and the true status of the observations as a measure of prediction error [23]. Explained Variation is calculated by
(7)
D(T) and Dx(T) are the overall measures of marginal and conditional predictive accuracy.
(8)
In this paper, the PVE measurement has been calculated adjusting for the important clinical variables.
Likelihood difference: (2) Cox proportional hazard model for overall survival, adjusted for significant clinical variables from preliminary analysis and an indicator variable for each of the stage groups of a given scheme;
(4) Cox proportional hazard model for overall survival, only contains significant clinical variables from preliminary analysis
Analogously, we used a parametric approach to evaluate this score in our new criteria, where we compare the model with only an indicator variable for each stage grouping of a given scheme, to the null model with no covariates. This measurement is to assess the improvement of fit of the model with stage grouping and clinical factors comparing to the model only contains clinical factors. This score of likelihood difference was then calculated based on the likelihood ratio test statistic for each scheme (Equation 9).
(9)
Both Explained Variation and Likelihood Difference can be used to evaluate outcome prediction of the stage scheme [17].
Balance: Finally, “Balance” was evaluated in the same way as before (Equation 3).
The actual score for each criterion for each of the scheme was normalized and then summarized by using the sum of the component scores, which puts equal weight on all five measurements. The stage grouping schemes were then ranked within the summary scores with the lowest summary score ranking first. Given the fact that the criterion of “balance” may be of less importance clinically, we also tried different weighting methods for this criteria.
Validation
Bootstrap validation: Bootstrap method was implemented as an approach to internally validate the results and evaluate the robustness of our new criteria. Theoretically, bootstrapping is a statistical method for assigning accuracy measures to sample estimates [24]. The basic idea of bootstrapping is that inference about a population can be modeled by resampling the sample data and performing inference on the resampled datasets. The bootstrap resamples can be treated as the “population” and hence the quality of inference from resampled data to the real sample is measurable.
Based on the original data set, 1000 bootstrap samples data sets were generated using sampling with replacement algorithm. For each of these bootstrap data sets, we applied our new criteria on each of the grouping scheme and calculate the summarized scores and ranks. Overall, 1000 summarized scores and ranks were created. To summarize the result, the average summarized score was reported as the bootstrap score and the bootstrap rank was calculated based on the bootstrap score. We also reported the proportion of being ranked at top choices for each scheme.
Multiple Imputation validation: Additional validation was performed using multiple imputations on patients with unknown HPV status. First, we construct the imputation model using the 810 patients with known HPV status (573 HPV+ and 237 HPV- patients). The imputation model was used to predict HPV status by logistic regression method using significant clinical factors [25]. Multiple imputations were applied on the 298 patients with unknown HPV status. The imputed HPV positive patients were used to validate the stage performance. The evaluation scores are standardized and averaged over the imputed data sets before ranking the stage methods.
Results
The summary statistics of the HPV+, HPV-, and HPV unknown subgroups were presented in Table 1. Kaplan-Meier curves for existing scheme were presented in Figure 2 and Figure 3. For HPV+ OPC cohort (Figure 2), only Kiricuta scheme shows a correct risk ordering, where the risk is increasing as the level of stages goes up from I to IV. All other existing schemes have incorrect risk ordering and cannot separate different stages very well. On the contrary, curves for all existing schemes in HPV- OPC cohort (Figure 3) are well separated with correct risk ordering. This observation can be explained by the fact that UICC/AJCC was developed mainly based on the HPV- OPC cohort and all other schemes aimed to improve UICC/AJCC.
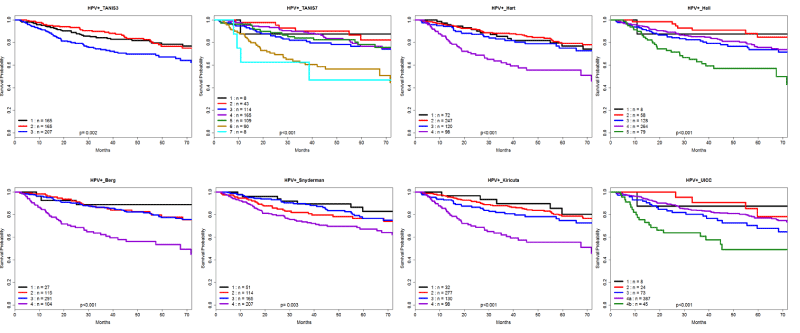
Figure 2: Kaplan-Meier curves of overall survival for existing schemes (HPV+ OPC cohort).
HPV-positive
HPV-negative
HPV unknown
Total case No.
573
237
298
Age (median)
57.8
65.6
58.4
Gender (male)
454 (79%)
171 (72%)
232 (78%)
Smoking pack-years (median)
40
15
25
Stage III-IV
540 (94%)
198 (84)
266 (89%)
Treatment (CRT)
285 (50%)
61 (26%)
101 (34%)
Subsite Tontil/BOT
541 (94%)
169 (71%)
245 (82%)
N2b-N3
399 (70%)
124 (52%)
169 (57%)
T1-T3
469 (82%)
166 (70%)
236 (79%)
Alcohol non-drinker/light/Moderate
442 (77%)
113 (48%)
196 (66%)
Table 1: Characteristics of Oropharyngeal Cancer Patients Treated in 2000- 2010.
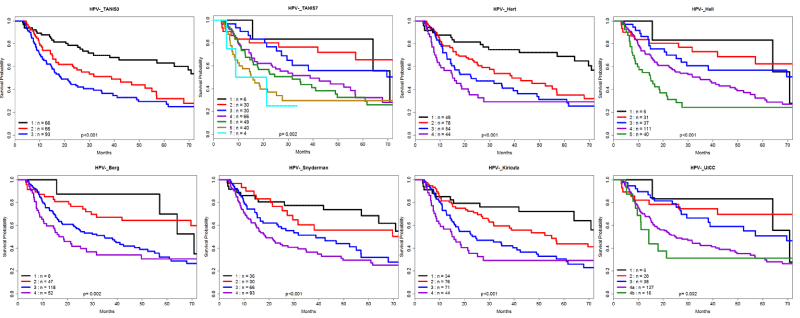
Figure 3: Kaplan-Meier curves of overall survival for existing schemes (HPV- OPC cohort).
Since all the existing stage grouping schemes work well on HPVOPC cohort, we focused our analysis on HPV+ OPC cohort and developed the new stage grouping scheme for HPV+ OPC cohort. Eight existing schemes and the new schemes were evaluated under both existing and new evaluation criteria (Figure 4).
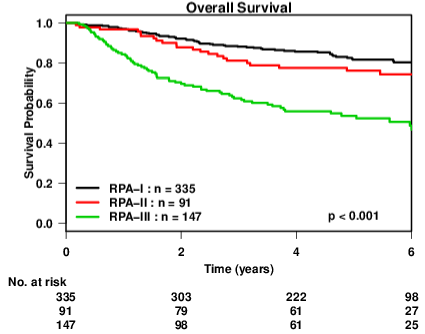
Figure 4: Kaplan-Meier curves of overall survival for new RPA scheme
(HPV+ OPC cohort).
Evaluation of schemes under existing criteria
Table 2 presents the standardized, weighted scores for each criterion along with the summary score and rankings. The higher the score, the worse a scheme performed. The overall evaluation under Existing Criteria ranked TANIS7 as the top one which has the best performance in Hazard Discrimination (Table 2). RPA stage ranked second, with the best performance in Hazard Consistency, Explained Variation and Slope. UICC/AJCC did worst with lowest Hazard consistency, Explained Variation, Slope and Balance. However, the existing criterion of hazard discrimination did not take into consideration the risk ordering (i.e. higher risk for subjects with higher stage level); therefore TANIS7 with well separated survival curves but a wrong risk ordering ranked first under this criterion.
Performance Evaluation Using Existing Criteria
RPA
Kiricuta
TANIS3
Hart
TANIS7
Snyderman
Hall
Berg
UICC
Hazard Consistency
0.04
0.05
0.07
0.05
0.05
0.07
0.06
0.05
0.08
Score
0.00
0.57
1.59
0.69
0.49
1.47
0.89
0.69
2.00
Rank
1
3
8
4
2
7
6
5
9
Hazard Discrimination
0.46
0.44
0.49
0.42
2.85
1.62
1.26
0.25
0.57
Score
1.84
1.85
1.81
1.87
0.00
0.95
1.22
2.00
1.75
Rank
6
7
5
8
1
2
3
9
4
Explained Variation
11.63
9.57
4.78
7.56
7.56
4.34
6.19
7.09
0.81
Score
0.00
0.38
1.27
0.75
0.75
1.35
1.01
0.84
2.00
Rank
1
2
7
4
3
8
6
5
9
Slope
0.11
0.10
0.04
0.10
0.10
0.04
0.08
0.10
0.01
Score
0.00
0.08
1.26
0.13
0.16
1.23
0.57
0.08
2.00
Rank
1
3
8
4
5
7
6
2
9
Balance
0.37
0.46
0.32
0.37
0.66
0.54
0.67
0.63
1.10
Score
0.07
0.18
0.00
0.06
0.44
0.28
0.44
0.40
1.00
Rank
3
4
1
2
7
5
8
6
9
Overall Score
1.88
2.75
4.66
3.03
1.17
3.84
3.12
3.35
6.25
Overall Rank
2
3
8
4
1
7
5
6
9
Table 2: Consistency, discrimination, variation explained, slope and balance scores and ranks for each scheme.
Evaluation of schemes under new criteria
Hazard consistency: The difference on model-fitting statistic between the model using stage groups proposed by scheme and the model using all 24 TN subgroups ranged from a low of 0.98 for the RPA scheme (Table 3), demonstrating the best hazard consistency, to a high of 3.48 for the UICC/AJCC, demonstrating the worst consistency.
Hazard discrimination: The hazard discrimination measure varied from a low of 0.28 for UICC to a high of 5.21 for Berg (the worst scheme by this criterion) (Table 3). RPA ranked 4th out of 9 schemes, with a score of 0.71.
Explained variation: After important clinical factors being taken into account, RPA was still the best scheme for predicting the hazard associated with HPV+ OPC, with 19.04% of the variance in survival explained. UICC/AJCC scheme did worst, with 11.50% of the variance explained.
Likelihood difference: The likelihood difference measure ranged from 2.31 for UICC/AJCC (the worst scheme) to 27.99 for RPA (the best scheme).
Balance: The score of “Balance” was the same as that under the existing criteria. TANIS3 did best in splitting the patient population into evenly sized groups, with a deviation score of 0.32. RPA stage performance third with score at 0.37. UICC/AJCC did worst at 1.10.
Summary scores: Table 3 also presents the standardized, weighted scores for each criterion along with the summary score and rankings. The higher the score, the worse a scheme performed. Overall, RPA stage ranked first, with the best performance in Hazard consistency, Explained Variation, Likelihood Difference, and the third best performance in Balance. Its score of 0.16 was followed by Kiricuta at 1.01. UICC/AJCC did worst with a score of 3.00, and it ranked worth in four of the five measurements.
Bootstrap result of scheme evaluation under new criteria
To assess the robustness of the assessment, we applied the new criteria on 1000 bootstrap samples generated based on our population. Average raw scores of each criterion and the average standardized scores for each stage grouping scheme were reported in Table 4. The overall scores were calculated by summing up the standardized scores of the five criteria. We also reported the percentage of times in which the scheme was ranked first or second.
Performance Evaluation Using Internal Validation by Bootstrap Algorithm
RPA
Kiricuta
TANIS3
Hart
TANIS7
Snyderman
Hall
Berg
UICC
Hazard Consistency
2.22
2.52
3.86
2.64
2.67
3.94
3.22
2.39
4.73
Score
0.07
0.18
0.68
0.23
0.24
0.71
0.44
0.13
1.00
Rank
2.22
2.91
7.12
3.92
3.92
7.73
5.84
2.37
8.97
Hazard Discrimination
1.89
3.42
1.13
5.04
4.07
1.30
3.10
6.17
1.37
Score
0.23
0.44
0.12
0.67
0.59
0.15
0.43
0.84
0.19
Rank
4.16
6.30
3.27
8.17
7.65
3.99
6.43
8.95
4.08
Explained Variation
18.45
16.98
13.58
15.71
15.60
13.27
14.50
15.41
11.18
Score
0.03
0.21
0.64
0.37
0.38
0.68
0.52
0.42
0.94
Rank
1.49
2.37
6.75
4.19
4.27
7.27
5.77
4.37
8.47
Likelihood Difference
28.83
17.96
11.65
17.18
9.82
8.53
10.77
18.87
3.27
Score
0.00
0.42
0.67
0.45
0.74
0.79
0.70
0.38
1.00
Rank
1.03
2.93
5.67
3.69
6.70
7.46
6.02
2.52
8.98
Balance
0.38
0.48
0.32
0.37
0.68
0.55
0.68
0.63
1.09
Score
0.10
0.23
0.03
0.10
0.48
0.31
0.48
0.43
1.00
Rank
2.34
4.13
1.64
2.21
7.24
4.77
7.37
6.30
9.00
Overall Score
0.42
1.16
1.49
1.40
1.87
1.91
1.96
1.80
3.16
Overall Rank
1
2
4
3
6
7
8
5
9
% Rank = 1
883
81
6
19
2
0
0
9
0
% Rank = 2
52
605
115
142
12
0
6
68
0
Table 4: Scores and ranks for each scheme under new criteria (based on 1000 bootstrap replications).
RPA ranked first with an overall score of 0.42 and the best performance in Hazard consistency, Explained Variation, and Likelihood Difference. It was ranked first in 883 out of 1000 replications and ranked second 52 times. UICC/AJCC ranked the last, indicating its worst performance under this new evaluation criteria. Overall, the bootstrap evolution confirmed the conclusion shown in Table 3.
Performance Evaluation Using New Criteria
RPA
Kiricuta
TANIS3
Hart
TANIS7
Snyderman
Hall
Berg
UICC
Hazard Consistency
0.98
1.26
2.60
1.38
1.48
2.66
1.99
1.15
3.48
Score
0.00
0.12
0.65
0.16
0.20
0.67
0.41
0.07
1.00
Rank
1
3
7
4
5
8
6
2
9
Hazard Discrimination
0.71
2.27
0.30
3.92
2.72
0.41
1.97
5.21
0.28
Score
0.09
0.41
0.01
0.74
0.50
0.03
0.34
1.00
0.00
Rank
4
6
2
8
7
3
5
9
1
Explained Variation
19.04
17.61
14.11
16.26
16.08
13.78
15.02
15.93
11.50
Score
0.00
0.19
0.65
0.37
0.39
0.70
0.53
0.41
1.00
Rank
1
2
7
3
4
8
6
5
9
Likelihood Difference
27.99
17.06
10.95
16.27
8.56
7.74
9.67
17.83
2.31
Score
0.00
0.43
0.66
0.46
0.76
0.79
0.71
0.40
1.00
Rank
1
3
5
4
7
8
6
2
9
Balance
0.37
0.46
0.32
0.37
0.66
0.54
0.67
0.63
1.10
Score
0.07
0.18
0.00
0.06
0.44
0.28
0.44
0.40
1.00
Rank
3
4
1
2
7
5
8
6
9
Overall Score
0.16
1.01
1.31
1.37
1.71
1.72
1.82
1.88
3.00
Overall Rank
1
2
3
4
5
6
7
8
9
Table 3: Scores and ranks for each scheme under new criteria.
Multiple imputation results
Besides that validation using bootstrap datasets, we applied multiple imputation using the 298 HPV unknown patients. Based on logistic regression model, we constructed the imputation model using significant HPV related clinical factors such as age (continuous), gender, sub site (Tontil/BOT vs. others), smoke Pack-Year (PY) (<=10 PY vs. >10 PY), N (N0-N2a vs. N2b-N3), T (T1-T3 vs. T4ab), and alcohol drinking (ex-drinker/heavy/unknown vs. non-drinker/ light/Moderate. The predictive ability of the imputation model is high (AUC=0.825). The imputation model was applied on the HPV unknown data to predict HPV+ status. The overall scores were calculated by summing up the standardized scores of the five criteria in Table 5. The overall rank of the multiple imputations results was also provided based on the overall score.
Performance Evaluation Using Multiple Imputations
RPA
Kiricuta
TANIS3
Hart
TANIS7
Snyderman
Hall
Berg
UICC
Hazard Consistency
1.10
1.11
1.25
1.27
1.06
1.27
0.95
1.18
1.39
Score
0.28
0.28
0.64
0.67
0.25
0.68
0.00
0.57
0.86
Rank
3.40
3.20
6.00
7.00
3.40
7.00
1.00
6.40
7.60
Hazard Discrimination
0.56
0.52
0.38
0.48
0.97
0.62
0.93
0.21
1.22
Score
0.39
0.35
0.26
0.25
0.71
0.35
0.58
0.09
0.71
Rank
4.40
4.40
4.20
4.00
7.20
5.00
6.20
2.20
7.40
Explained Variation
15.11
16.45
15.32
15.37
16.72
15.42
17.49
16.18
13.84
Score
0.68
0.21
0.62
0.54
0.21
0.54
0.02
0.48
0.79
Rank
7.40
3.20
6.40
5.60
3.00
6.00
1.60
5.00
6.80
Likelihood Difference
9.03
6.27
7.38
5.23
3.86
5.26
5.76
5.82
4.41
Score
0.00
0.51
0.31
0.71
0.96
0.70
0.61
0.60
0.85
Rank
1.00
3.40
2.20
6.00
8.60
6.00
5.20
5.60
7.00
Balance
0.27
0.41
0.30
0.28
0.68
0.53
0.71
0.62
1.05
Score
0.04
0.21
0.07
0.05
0.54
0.36
0.58
0.48
1.00
Rank
1.80
4.20
2.00
2.20
6.80
4.80
8.00
6.20
9.00
Overall Score
1.05
1.20
1.44
1.60
2.09
2.01
1.47
1.68
3.38
Overall Rank
1
2
3
5
8
7
4
6
9
Table 5: Scores and ranks for each scheme under new criteria (based on multiple imputations on unknown HPV status).
RPA stage ranked first with an overall score of 1.05 and the best performance in Explained Variation, Likelihood Difference, and Balance. UICC/AJCC ranked the last, indicating its worst performance which is consistent to the bootstrap validation results.
Discussion
All existing stage grouping schemes do not take the effects of important clinical factors (e.g. treatment) into consideration in the development process, although their development are all based on historical data. Based on this observation, we proposed new criteria to evaluate performances of different schemes, with key clinical factors adjusted in the evaluation process. Given the fact that within HPV+ OPC cohort, all existing stage schemes have incorrect risk ordering and cannot separate different stages very well, we proposed a new stage grouping schemes, which was shown to have superior performance over all existing schemes.
The assumptions underlying the use of the UICC/AJCC scheme in head and neck cancer are that the groups consist of patients with similar disease severity and that the differences in severity among the groups are meaningful. We have shown that, for HPV+ oropharynx cancer, these assumptions do not hold. For both existing and new criteria, UICC/AJCC did worst among all schemes.
By presenting the results for each measurement separately, the researchers can focus on the property that is most relevant to their specific research purpose. Based on our scoring system, within the HPV+ cohort, RPA stage scheme performed better than the rest, and the results were verified using bootstrap validation algorithm and multiple imputations. We also tried different weightings on each measurement (e.g. gave less weight to the “Balance” score) and obtained consistent conclusion, where RPA stage was still the best scheme and UICC/AJCC was ranked last (results not shown).
All the existing stage grouping schemes were developed based on historical data, where important clinical factors like treatment and smoking behavior have huge impact on the survival outcome that cannot be ignored. Therefore, we incorporated those key factors into the new criteria and applied the parametric approach to evaluate stage grouping schemes by using the likelihood ratio statistic from Cox proportional hazards model. Besides that, it also improves the existing criteria from other aspects. First, in the new criteria, we measured the predictive ability of a certain grouping scheme by using the percent of the variance in the hazard rates explained by a given grouping scheme, and the likelihood difference between the model with and without grouping scheme. The “Slope” measurement was removed because it largely depends on the follow-up time of patients and those who were censored or dead before 3 years followup must be excluded from the analysis, which introduces bias in the evaluation. Second, in addressing hazard discrimination, the existing criteria measures how evenly the group survival curves are spaced and how large a survival rate difference they span. However, it does not take into consideration the correct risk ordering, which means a scheme with well separated survival curves but a wrong risk ordering may get a high score on this criterion. It is shown from the Kaplan- Meier curves that the risk ordering of most existing stage grouping schemes is not correct for HPV+ OPC cohort; therefore the existing measurement on hazard discrimination is not appropriate. In the new criteria, we used the parametric approach to measure the risk discrimination and difference between groups within a given scheme. This method gives schemes with correct risk ordering higher scores than those with incorrect ordering. Furthermore, the current criteria were based on the non-parametric modeling using only monthly rate, the new criteria use parametric evaluation and takes into according all the follow up information of the survival outcomes to provide more precise evaluation on the grouping schemes.
For the TNM grouping schemes, some were developed based on clinical understanding of the disease processes (i.e. UICC/AJCC); the others were developed based on historical observations including the newly developed schemes. However, a single disease cohort may have sample variation and causes biased scheme selection by chance. Our bootstrap procedure and multiple imputations provided convincing validation to the robustness of the scheme performance. It also demonstrated the robustness of new evaluation criteria.
Summary Statement
It is worth to point out that HPV+ and HPV- OPC cohort are fundamentally different in the survival performance, therefore it is recommended to develop a new stage grouping scheme for HPV+ cohort as a separate disease site. Currently, UICC/AJCC is derived mainly based on HPV- OPC patients, and other existing schemes aim to improve the prognostic ability of UICC/AJCC, but without paying enough attention on the distinction between the two HPV cohorts. The new stage grouping scheme we proposed was designed based on HPV+ OPC cohort, and we have shown that this new scheme outperforms all existing grouping schemes; the results are robust within the datasets under bootstrap validation and multiple imputations.
Our findings need to be further validated in additional research since the patient population basis as well as the treatment practice may differ across different clinics. Ideally, the new scheme can outperform UICC/AJCC in head and neck cancer sub sites of lip, oral cavity, and oropharynx, hypopharynx, larynx and paranasal sinuses. However, as many studies have demonstrated [4-6], HPV+ OPC cohort has much better survival performance than HPV- OPC cohort, which may lead to the conclusion that no one scheme will serve both types of OPC.
Current stage grouping system only provides classification from the anatomic perspective and does not take into account tumorrelated factors or patient-related factors, which have significant prognostic value. As more and more studies recognized the importance of non-anatomic factors, how to incorporate them into the current system has become the main challenge. Admittedly, key prognostic factors for different disease sub sites are usually different. Therefore, it is not easy to propose a uniform grouping system with non-anatomic factors included for all sites. Further research may focus on developing new algorithms to construct prognostic models or prognostic nomograms, which will include both the anatomic and non-anatomic information.
In conclusion, no existing stage grouping scheme has good prognostic value in HPV+ OPC cohort. Therefore, we proposed the new scheme and it outperformed all existing schemes under the new criteria which incorporate non-anatomic information. In future research, we should aim to develop a prognostic system including non-anatomic factors as a companion to the current stage grouping scheme, which relies solely on anatomic information. The improvements made on the prognostic system will not only benefit clinical and research practice, but more importantly, will benefit the patients.
References
- Edge SB, Compton CC. The American Joint Committee on Cancer: the 7th edition of the AJCC cancer staging manual and the future of TNM. Ann Surg Oncol. 2010; 17: 1471-1474.
- Groome PA, Schulze K, Boysen M, Hall SF, Mackillop WJ. A comparison of published head and neck stage groupings in carcinomas of the oral cavity. Head Neck. 2001; 23: 613-624.
- O’Sullivan B, Shah JP. Head and Neck Cancer Staging and Prognosis: Perspectives of the UICC and the AJCC. Head and Neck Cancer. 2011; 135-155.
- Benson E, Li R, Eisele D, Fakhry C. The clinical impact of HPV tumor status upon head and neck squamous cell carcinomas. Oral Oncol. 2014; 50: 565-574.
- Rautava J, Kuuskoski J, Syrjanen K, Grenman R, Syrjanen S. HPV genotypes and their prognostic significance in head and neck squamous cell carcinomas. J Clin Virol. 2012; 53: 116-120.
- O'Sullivan B, Huang SH, Siu LL, Waldron J, Zhao H, Perez-Ordonez B, et al. Deintensification Candidate Subgroups in Human Papillomavirus–Related Oropharyngeal Cancer According to Minimal Risk of Distant Metastasis. Journal of Clinical Oncology. 2013: 31: 543-550.
- Jones GW, Browman G, Goodyear M, Marcellus D, Hodson DI. Comparison of the addition of T and N integer scores with TNM stage groups in head and neck cancer. Head Neck. 1993; 15: 497-503.
- Snyderman CH, Wagner RL. Superiority of the T and N integer score (TANIS) staging system for squamous cell carcinoma of the oral cavity. Otolaryngol Head Neck Surg. 1995; 112: 691-694.
- Hart AA, Mak-Kregar S, Hilgers FJ, Levendag PC, Manni JJ, Spoelstra HA, et al. The importance of correct stage grouping in oncology. Results of a nationwide study of oropharyngeal carcinoma in The Netherlands. Cancer. 1995; 75: 2656-2662.
- Kiricuta IC. The importance of correct stage grouping in oncology. Results of a nationwide study of oropharyngeal carcinoma in The Netherlands. Cancer. 1996; 77: 587-590.
- Berg H. Die prognostische relevanz des TNM-systems fur oropharynxkarzinome. Tumordiagn Ther. 1992; 13: 171-177.
- Hall SF, Groome PA, Rothwell D, Dixon PF. Using TNM staging to predict survival in patients with squamous cell carcinoma of the head and neck. Head Neck. 1999; 21: 30-38.
- Takes RP, Rinaldo A, Silver CE, Piccirillo JF, Haigentz M, Suarez C, et al. Future of the TNM classification and staging system in head and neck cancer. Head Neck. 2010; 32: 1693-1711.
- Gunderson LL, Jessup JM, Sargent DJ, Greene FL, Stewart AK. Revised TN categorization for colon cancer based on national survival outcomes data. J Clin Oncol. 2010; 28: 264-271.
- Sobin L, Gospodarowicz M, Wittekind C. International Union Against Cancer: TNM Classification of Malignant Tumours (Wiley-Blackwell, Chichester, United Kingdom). 7th edition. 2010.
- 16. Huang SH, Xu W, Waldron J, Siu L, Shen X, Tong L, et al. Refining American Joint Committee on Cancer/Union for International Cancer Control TNM Stage and Prognostic Groups for Human Papillomavirus-Related Oropharyngeal Carcinomas. J Clin Oncol. 2015; 33: 836-845.
- Schemper M. The explained variation in proportional hazards regression. Biometrika. 1990; 77: 216-218.
- Yates JF. External correspondence: decomposition of the mean probability score. Org Behav Hum Perform 1982; 30: 132-156.
- Arkes HR, Dawson NV, Speroff T, Harrell FE, Alzola C, Phillips R, et al. The covariance decomposition of the probability score and its use in evaluating prognostic estimates. Support Investigators. Med Decis Making. 1995; 15: 120-131.
- Hall SF, Groome PA, Irish J, O'Sullivan B. TNM-based stage groupings in head and neck cancer: application in cancer of the hypopharynx. Head Neck. 2009; 31: 1-8.
- Cox DR. Regression models and life-tables. J R Stat Soc B. 1972; 34: 187-202.
- Breslow NE. Analysis of survival data under the proportional hazards model. International Statistical Review/Revue Internationale de Statistique. 1975: 45-57.
- Schemper M, Henderson R. Predictive accuracy and explained variation in Cox regression. Biometrics. 2000; 56: 249-255.
- Cheng A, Yeager M. Bootstrap resampling for voxel-wise variance analysis of three-dimensional density maps derived by image analysis of two-dimensional crystals. J Struct Biol. 2007; 158: 19-32.
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: John Wiley & Sons, Inc. 1987.