
Special Article - Biostatistics Theory and Methods
Austin Biom and Biostat. 2015;2(2): 1018.
The Application of Last Observation Carried Forward in the Persistent Binary Case
Jun He and Donna McClish*
Department of Biostatistics, Virginia Commonwealth University, USA
*Corresponding author: McClish, Department of Biostatistics, Virginia Commonwealth University,Virginia.
Received: June 01, 2015; Accepted: June 11, 2015; Published: June 19, 2015
Abstract
The main purpose of this research is to evaluate use of Last Observation Carried Forward (LOCF) as an imputation method when persistent binary outcomes are missing in a Randomized Controlled Trial. A simulation study was performed to evaluate the effect of equal event rates and equal/unequal dropout rates on Type I error. Properties of estimated event rates, treatment effect, and bias were also assessed. LOCF was also compared to two versions of complete case analysis - Complete1 (excluding all observations with missing data), and Complete2 (only carrying forward observations if the event is observed to occur). The results showed that 1) If the dropout rates were equal, the three analysis methods all had appropriate Type I error; 2) If the dropout rates were unequal, the Type I error was much greater than 0.05 in both LOCF and Complete2 analysis; 3) Regardless of dropout rates, the estimated mean event rate was underestimated in the LOCF analysis and overestimated in the Complete2 analysis, while Complete1 analysis had the closest estimated mean event rate to the true rate; 4) Compared to the study with no event at the first time point, the estimated mean event rate was underestimated less in the LOCF analysis and overestimated more in the Complete2 analysis when an event could occur at the first time point. LOCF analysis was applied to a mammogram dataset, where the LOCF method underestimated the final event rate.
Keywords: Last observation carry forward; Persistent binary data; Missing data; Estimated mean event rate; Type I error; Bias
Abbreviations
RCT: Randomized Clinical Trial; ITT: Intent to Treat; LOCF: Last Observation Carried Forward; WISER: Women Improving Screening through Education and Risk Assessment; HBM: Health Belief Model
Introduction
In a Randomized Clinical Trial (RCT), patients often drop out before a study is completed because of side effects, recovery, lack of improvement, unpleasant health problems, and other unknown factors, which results in missing data [1]. Intent to treat (ITT) analysis – used in analyzing clinical trial data – is based on the initial treatment plan, and intends to analyze data from all the observations, even if the patients drop out of the study. When there are missing data, following ITT requires some kind of imputation be used. Although there are many missing data imputation methods, such as Last Observation Carried Forward (LOCF) [2], replacement with mean [3], regression imputation [4], multiple imputation [5], and maximum likelihood [6], no single method is appropriate for all problems.
The focus in this paper will be on the LOCF imputation method applied to persistent binary cases. A persistent phenomenon is defined as an event that once it occurs at a time point, it will occur at all the following time points. One example of persistent binary outcomes occurred in the Women Improving Screening through Education and Risk Assessment (WISER) study [7]. To assess a simple tailored health promotion intervention, the participants were asked whether they had a mammogram since the start of the study. Once participants had a mammogram the event persists.
Almost all clinical trials face the problem of missing data. For example, in the WISER study, a nearly 40% dropout rate was observed. Then the question becomes how to analyze a dataset with missing data. LOCF assumes that after the point of dropout the last observed outcome is used in place of missing observations. For continuous outcomes, this method is not recommended because it introduces bias, and alters the mean and variance [8,9]. For binary data, the LOCF imputation method not only has poor frequency properties of estimators when missing values are due to dropout, but also causes inflated Type I error rates [10]. This method may also have poor performance in analyzing binary outcomes if the event is a persistent phenomenon.
The purpose of this paper is to evaluate the LOCF imputation method in situations of persistent binary outcomes. A simulation study is performed to examine the effect of dropout rates and type of dropout (random or associated with treatment arm) on Type I error for the LOCF method of analysis. At the same time, the results from LOCF are compared to two versions of complete case analysis: Complete1 (excluding all observations with missing data), and Complete2 (excluding the missing data when the event hasn’t been observed to occur, but carrying forward the observations if the event is observed to occur).
observed to occur). Section 2 describes the simulation. Section 3 presents results of the simulation, allowing a comparison of the three analysis methods. In section 4, these methods are applied to a real life example using the WISER study. Finally, we summarize the study, discuss the limitations, and mention future work.
Simulation and Methods
Assumptions and parameters in the simulation
Simulations are performed by assuming an RCT with two treatment arms (Control and Treatment), equal sample sizes and three time points (T1, T2, and T3). Two study scenarios are considered. In one, it was assumed that the study event could not have occurred at time one. This would be typical for a clinical trial where T1 is baseline (prior to treatment) and having the event would be exclusion to enrolling in the study. In the second scenario, the first measurement (T1) could be assessed after treatment and the event may or may not occur at that time. In both studies, it was assumed no missing data at T1, and an equal likelihood that the missing data would first occur at T2 or T3. The persisted event is assumed, meaning that the subject will continue to have the event at future time points once a subject has the event. Monotone missing is also assumed, which can be explained as once a subject has missing data at a time point all future time points will also be missing.
For the event rates, we assume no treatment effect (equal event rate), allowing the Type I error rate to be assessed. Both equal and unequal dropout rates are considered (Table 1). For the case of equal dropout rate, 9 scenarios are considered, represented by a range of low, moderate and high event rates (0.2, 0.5, and 0.8), and low, moderate and high dropout rates (10%, 25%, and 40%). In the case of unequal dropout rates, 18 scenarios are investigated. Since the effect of unequal dropout could be influenced by how different the dropout rates are, two scenarios corresponding to each average dropout rate are considered. For example, when the average dropout rate is 10%, dropout rates of 12.5% vs. 7.5% and 15% vs. 5% are used in the control group and the treatment group respectively. For each set of parameters, 2000 replications are used for estimation and testing.
No Treatment Effect Case
Parameter
Values (Group1, Group2)
Scenario
Total Scenario
With equal dropout rate
Event Rate (equal)
(0.2,0.2), (0.5, 0.5), (0.8, 0.8)
3
3x3=9
Dropout rate (equal)
(10%, 10%), (25%, 25%), (40%, 40%)
3
With unequal dropout rate
Event Rate (equal)
(0.2,0.2), (0.5, 0.5), (0.8, 0.8)
3
3x6=18
Dropout rate (unequal)
(12.5%, 7.5%), (15%, 5%)
6
(30%, 20%), (40%, 10%)
(45%, 35%), (60%, 20%)
Note: “Group1” and “Group2” represent Control and Treatment groups. Since event rates are equal, results are the same regardless of which is considered Group1.
Table 1: Parameters in Simulation.
Simulation of full dataset and missing dataset
SAS statistical software (version 9.4) was used to simulate data and perform statistical analyses. The simulation primarily used SAS Interactive Matrix Language.
The full dataset was simulated as follows. We assumed a sample size of 100 per group (which is large enough to detect a 20% difference in groups with power 80%). Based on the assumed true event rate, events at T3 were created according to a Bernoulli distribution. If at T3 no event was observed, the event could not have occurred at an earlier time point, so a no event marker was created for previous time points (T2 and T1). However, if at T3 an event was observed, the time of its first occurrence had to be determined. If the event could occur at T1, then its first occurrence must have been at T2 or T3; we assumed this was equally probable and used a Bernoulli random variable with probability 1/2 to assign first occurrence. Similarly, if the event could occur at T1, we assumed this was also equally probably and used a Bernoulli random variable with probability1/3 to determine the time of first occurrence.
Once the full dataset was generated in both groups, the possible missing outcome patterns were implemented. First, we determined which people would and would not have missing observations, using a Bernoulli random variable with parameter equal to the dropout rate. We also assumed that there was no dropout at T1, and that, for those who dropped out, the probability of dropping out at T2 and T3 would be equal. Therefore we would be able to know where the missing data started (which observation and which time point). Once the missing data was observed, we assumed monotone dropout. If dropout rate was random, equal dropout rate was assumed in Control and Treatment groups. If dropout rate was related to group, then unequal dropout rate was assumed.
According to different data imputation methods, LOCF dataset, Complete1 dataset, and Complete2 dataset were created. Again, the LOCF method replaces missing observations with the observation previous to the time point that the first missing observation appeared. The Complete1 method excludes all observations with missing data. For the Complete2 dataset, instead of excluding all the observations with missing data, if the event were observed at T2, but missing at T3, we assumed that the event also occurred and was observed at T3.
Methods and statistical analyses
The primary analysis focuses on testing for a treatment effect, which is the difference of event rates. The difference of estimated event rates between groups will be analyzed using the two sample proportion z-test.
where
RT is the event rate of the treatment group, and RC is the event rate of the control group, and R0 is the pooled event rate for the entire sample. NT is the number of subjects in the treatment group, and NC is the number of subjects in the control group. In the full dataset and LOCF dataset, NT=NC. In the two Complete data sets, the sample sizes are not equal because observations are deleted depending on the missing value pattern. Each replication will have a Z test statistic calculated. Since the null hypothesis is no treatment effect the number of times that the absolute value of Z exceeds Z0.05 (=1.96) over all replications will be counted. When the null hypothesis is true, the proportion will be the Type I error, which is expected to be around 5%.
The bias in the estimated treatment effect can be expressed as the difference between the estimated and the true treatment effect, where RC0 is the assumed true event rate in the control group, and RT0 is the assumed true event rate in the treatment group. Since this simulation assumes equal event rates (RC0- RT0=0), bias in the estimation of treatment effect is equal the estimated treatment difference
Results and Application
Equal dropout rate
Three event rates (0.2, 0.5, and 0.8) and equal dropout rates (10%, 25%, and 40%) were assumed. The results (Figure 1) showed that the mean event rate was underestimated when LOCF analysis was used but was overestimated using Complete2 analysis, while Complete1 analysis had estimated mean event rate very close to the true event rate. Since the pattern for each event rate under different dropout rates was the same, only the highest event rate (0.8) was presented. When the dropout rate increased, the amount of underestimation of the mean event rate increased when the LOCF was used. The results also showed that the underestimation for LOCF was large while the overestimation for Complete2 analysis was relatively small. Furthermore, it was interesting to see that the estimated mean event rate was less underestimated in the LOCF analysis and more overestimated in the Complete2 analysis in the case where the event might occur at T1 as compared to the case when no events occur at T1. For example, when the event rates are 0.8, and the event rate cannot occur at T1, dropout rates of 10%, 25%, and 40% lead to estimated mean event rates of 0.74, 0.65 and 0.56 for LOCF, but 0.80, 0.81 and 0.82 for Complete2 respectively. Yet when the event could occur at T1, the estimated mean event rates were 0.76, 0.70 and 0.64 for LOCF, but 0.81, 0.82 and 0.84 for Complete2.
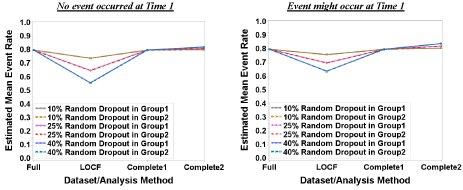
Figure 1: Estimated Mean Event Rate: Equal Event Rate (0.8) and Unequal Dropout Rate.
Even though the mean event rate was underestimated when LOCF was used and overestimated when Complete2 was used in general, the difference in rates between two groups was near zero in both analyses. The results showed that the bias was close to 0 (Table 2). (Table 3) showed the proportion of times that the test of significant difference between the two event rates was rejected. Since no treatment effect was assumed, a rejection rate of 5% was expected. The result also showed that all type I error rate estimates in the equal drop-out cases were within +/- 2% of the nominal 5% level.
Event Rate
Dropout Rate
Bias
No event occurred at T1
Event might occur at T1
LOCF
Complete1
Complete2
LOCF
Complete1
Complete2
20%
10%
0.002
0.002
0.002
0.002
0.002
0.002
25%
0.001
0.003
0.002
0.002
0.003
0.003
40%
0.002
0.004
0.003
0.002
0.004
0.002
50%
10%
0.002
0.003
0.002
0.003
0.003
0.003
25%
0.002
0.002
0.003
0.003
0.002
0.003
40%
0.003
0.003
0.003
0.002
0.003
0.003
80%
10%
0.000
0.001
0.001
0.000
0.001
0.001
25%
0.001
0.001
0.001
0.000
0.001
0.000
40%
0.002
0.001
0.001
0.002
0.001
0.001
Table 2: Bias: Equal Dropout Rate.
Event Rate
Dropout Rate
Type I error
No event occurred at T1
Event might occur at T1
Ave.
Gp1
Gp2
LOCF
Complete1
Complete2
LOCF
Complete1
Complete2
20%
10%
10
10
0.050
0.055
0.052
0.051
0.055
0.049
12.5
7.5
0.051
0.050
0.050
0.050
0.050
0.050
15
5
0.056
0.049
0.049
0.054
0.049
0.054
25%
25
25
0.046
0.046
0.048
0.049
0.046
0.050
30
20
0.058
0.049
0.053
0.052
0.049
0.060
40
10
0.128
0.047
0.064
0.085
0.047
0.104
40%
40
40
0.044
0.046
0.045
0.049
0.046
0.045
45
35
0.051
0.044
0.051
0.052
0.044
0.061
60
20
0.217
0.042
0.094
0.111
0.042
0.190
50%
10%
10
10
0.054
0.052
0.051
0.056
0.052
0.049
12.5
7.5
0.057
0.055
0.055
0.053
0.055
0.056
15
5
0.082
0.055
0.053
0.061
0.055
0.059
25%
25
25
0.053
0.052
0.050
0.057
0.052
0.054
30
20
0.087
0.051
0.054
0.066
0.051
0.054
40
10
0.361
0.047
0.066
0.187
0.047
0.114
40%
40
40
0.041
0.044
0.044
0.052
0.044
0.047
45
35
0.074
0.048
0.046
0.065
0.048
0.057
60
20
0.598
0.049
0.101
0.301
0.049
0.241
80%
10%
10
10
0.055
0.051
0.048
0.054
0.051
0.050
12.5
7.5
0.080
0.053
0.051
0.067
0.053
0.056
15
5
0.151
0.054
0.053
0.096
0.054
0.058
25%
25
25
0.047
0.054
0.050
0.055
0.054
0.053
30
20
0.145
0.050
0.050
0.098
0.050
0.055
40
10
0.761
0.048
0.059
0.468
0.048
0.086
40%
40
40
0.054
0.053
0.056
0.049
0.053
0.059
45
35
0.140
0.051
0.052
0.095
0.051
0.058
60
20
0.944
0.050
0.080
0.664
0.050
0.159
Note: “Ave.” represents average dropout rate. “Gp1” and “Gp2” represent Group1 and Group2. Since event rates are equal, results are the same regardless of which is considered the Control group.
Table 3: Type I Error: Equal and unequal dropout rates.
Unequal dropout rate
The mean event rates were estimated under the assumption of equal event rate (0.2, 0.5 or 0.8) and unequal dropout rate. Note that since event rates are equal, results are the same regardless of whether the dropout rate is higher in the Treatment or Control group, thus tables and figures simply refer to Group1 and Group 2. Similar to the results under the condition of equal dropout rate, mean event rates were underestimated using LOCF analysis and overestimated using Complete2 analysis; Complete1 analysis still had estimates of mean event rate close to the true rate (Figure 2). (Figure 3) displayed the bias in estimated treatment difference for equal event rates of 0.8 and unequal dropout rate. In LOCF and Complete2 analysis, for each equal event rate case the absolute bias increased as the difference between dropout rates increased under a fixed average dropout rate. For example, when no event can occur at T1, and the average dropout rate was 40%, the absolute bias with LOCF analysis increased from 0.058 to 0.241 as the dropout difference increased from 10% to 40%, while with Complete2 analysis the absolute bias increased from 0.01 to 0.038. It was interesting to see that under any fixed equal event rate and fixed difference of dropout rate the bias was stable in LOCF analysis (Figure 3a). For example, under the assumption of equal event rate of 0.8, if the dropout difference was 10%, regardless of average of dropout rates the absolute bias was 0.06. However, in Complete2 analysis instead of observing similar bias, we observed that under the same dropout difference the bias was slightly increased as the average dropout rate increased (Figure 3a). For instance, under the assumption of equal event rate of 0.8 and dropout difference of 10%, the bias increased from 0.006 to 0.007 to 0.01 as the average dropout rate increased from 10% to 25% to 40%. (Figure 3b) showed the same pattern as (Figure 3a).
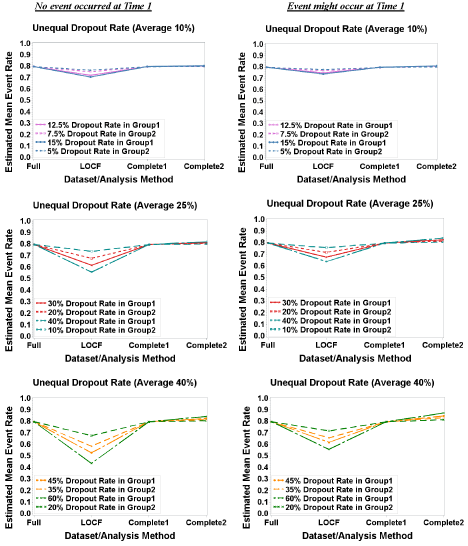
Figure 2: Estimated Mean Event Rate: Equal Event Rate (0.8) and Unequal Dropout Rate.
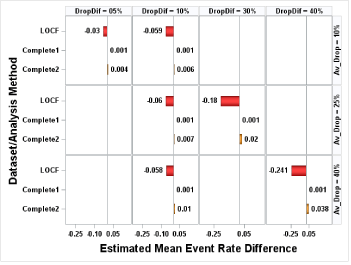
Figure 3a: No event occurred at Time 1.
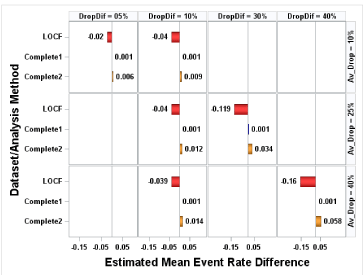
Figure 3b: Bias: Equal Event Rate (0.8) and Unequal Dropout Rate. Event
might occur at Time 1.
(Table 3) has the estimated Type I error rates. If the event rate was low (0.2) and dropout rate was very low (average 10%), the dropout rate did not have much effect on Type I error in each analysis, which was close to 0.05. In contrast to results for equal dropout rates, however, the Type I error in LOCF analysis increased when the difference of the dropout rates increased. When the equal event rate was 0.2 and dropout difference was 40%, the Type I error was 0.217 and it was 0.944, when equal event rate was 0.8 with 40% dropout difference. With an estimated Type I error rate as high as 0.944 (rather than the desired 0.05), LOCF analysis should not be used in cases of unequal dropout rates. Complete2 analysis also behaved poorly for higher event rate with bigger difference of dropout rate (Table 3). The Type I error of 0.101 was observed under equal event rate of 0.5 and dropout difference of 40%. This result was not as extreme as that of the LOCF analysis.
Application
In this section we illustrate the missing imputation methods using an example from a study of breast cancer screening - the WISER study [7]. The purpose of WISER was to assess whether a simple, tailored health promotion intervention would increase mammography screening rates. Subjects were randomly assigned to an Intervention group (449 participants) or a Control group (450 participants).Risk for breast cancer was assessed at baseline using the Gail Model [11]. The intervention group received, at baseline, recommendations tailored to their individual risk category, including information based on the Health Belief Model (HBM) such as barriers to mammography, the seriousness of breast cancer, and benefits of yearly mammograms. The control group only received general information about breast cancer prevention practices, but no individual recommendations, no HBM report, and no risk report. Subjects were followed at 1 month, 6 months and 18 months after randomization and intervention. They were asked at each follow-up time point if they had gotten a mammogram since enrolling in the study. The primary question was whether there was a difference of mammogram rates at the 18th month follow-up between intervention and control groups.
If subjects responded at all the follow-ups, analysis would be straightforward. Only a z-test was needed to be performed in analyzing the 18th months’ follow-up on mammogram. However, as is typical, there was missing data. The question became how to analyze data when the dataset was incomplete. Our simulation investigated 3 methods, which we applied here.
No mammogram was assumed at baseline. Occasionally a subject who did not respond at an earlier follow-up time point responded to a later follow-up. This violates the assumption of monotone dropout. For purposes of this paper, though, the data were altered to force the assumptions to hold by ignoring later responses (considering them to be missing). In addition to the self-reported mammography data, information was obtained from medical records and the health information system. It was assumed that if there was no report of a mammogram from self-report, medical records or the information system, and then no mammogram had been done. This was used to construct a gold standard or “full dataset”.
Participants in the WISER study were between 40 and 82 years old, with 56% under the age of 50. Half of the participants were Caucasian and 59% had at least some college education. The dropout rate in the control group increased from 21% at month 1 to 35% at month 6, and 41% at month 18, while in the intervention group the dropout rate was 17%, 37% and 43% at month 1, 6 and 18, respectively. It appeared reasonable to expect results to be similar to those presented in our simulation with equal dropout.
For analysis of the mammogram data, the final event rates were different in the four datasets (Table 4). At 18 months, in the full dataset 74.89% and 73.05% of the sample had a mammogram in the control group and the intervention group respectively - a scenario of equal event rate. In the LOCF analysis, the estimated mammogram rates (58.22% and 56.79% in the control group and the intervention group respectively) appeared to be underestimated. In the Complete2 analysis, much higher event rates (>84%) were observed in both groups. The sample sizes were decreased almost 40% in the Complete1 and Complete2 analyses (Table 4).
Full
LOCF
Complete1
Complete2
Con.
Int.
Con.
Int.
Con.
Int.
Con.
Int.
Analysis Sample Size
450
449
450
449
259
256
298
302
Event rate
74.9
73.0
58.2
56.8
86.1
81.6
87.9
84.4
Note: “Con.” represents Control group; “Int.” represents Intervention group.
Table 4: Analysis sample size and event rates (%).
The Z-test was performed for each analysis method to test if there was an intervention effect. None of the p-values of the test statistics were less than 0.05 (Table 5), so the null hypothesis could not be rejected, implying that we could not find evidence to show significant difference under a=0.05. Based on the simulation results when there was no treatment effect, while the actual event rates may be biased, the expected bias for treatment effect using LOCF, Complete1, and Complete2 should be close to 0, which could be ignored.
Z-test Statistic for Mammogram
Group
Full
LOCF
Complete1
Complete2
Event Rate Difference
0.0184
0.0143
0.0446
0.0348
Z-test Statistic
0.629
0.434
1.376
1.235
p-value (two-tailed)
0.529
0.664
0.169
0.217
Significance
No
No
No
No
Table 5: Analysis Results: Mammogram data.
In the mammogram data analysis, LOCF underestimated the final event rate, and Complete2 overestimated final event rate for mammography (assuming that the “full dataset” represents the truth). In this dataset, Complete1 also overestimated the final event rate and the estimated event rates in Complete1 and Complete2 analyses were very close. However, the previous simulation study showed that Complete1 tended to have estimates similar to the full dataset. One possible explanation for the conflict might be that the “full” dataset in the mammogram was probably not accurate. It was based on the assumption that if there were missing self-reported data, and no other sources (such as the chart or info systems) indicated that the subject had a mammogram, and then they did not have had a mammogram. Mammograms at an outside institution would not have been noted.
When the “full” dataset was used as a reference for the mammography data, it was reasonable to think that this was an application of the simulation study under the scenario of equal dropout rate and equal event rate. Even though the z-test in the LOCF analysis showed that there was no significant effect between the control group and the intervention group in this mammogram data analysis, it was not a good imputation method to analyze missing data because it also underestimated the individual event rates.
Discussion
This paper evaluated the application of the LOCF method with persistent binary data, assessing Type I error, estimated event rate, treatment effect, and bias. The simulation study showed that regardless of whether the dropout rate was equal or unequal, the mean event rate was underestimated using LOCF analysis, slightly overestimated using Complete2 analysis, and unbiased using Complete1 analysis. It was useful to try to understand why in LOCF analysis fewer events were observed at T3 than in the full dataset. Whether it was assumed that events could or could not occur at T1, if missing data occurred at T2, the outcome of no-event would be carried forward to T3. Therefore, we would observe lower event rates at T3 in LOCF analysis. Thus the phenomenon of underestimated mean event rate appeared in LOCF analysis, regardless of dropout rate. In Complete2 analysis, the missing data was excluded when the event hadn’t been observed to occur, but if the event was observed to occur, the data was kept and the observation was carried forward. Since it only excluded the entire missing observations with no event occurred in the last observation, Complete2 analysis had a higher percentage of events observed at the end of the study than the full dataset, which caused the mean event rate at T3 to be slightly overestimated. It was interesting to notice that compared to the situation when no events could occur at T1, the estimated mean event rate was underestimated less in LOCF analysis and overestimated more in Complete2 analysis when the an event could occur at T1.
The results also showed that neither LOCF analysis nor Complete2 analysis was a good choice for missing data imputation in the longitudinal binary data analysis due to poorly estimated event rates and the bias involved. If finding the treatment effect was the only interest, LOCF analysis could be used in the case of equal event rate and equal dropout rate. This was the only case that LOCF analysis showed proper Type I error around 0.05.But in practice we will not know whether event rates are equal. However, if we were interested in estimated mean event rates, Type I error, LOCF analysis and Complete2 analysis were both bad choices. Complete1 analysis seemed to behave well, but it was not practical. At the beginning of the study, we assumed that once the event happened, it persisted. Complete1 analysis excluded all the random missing observations, even though we observed the event in a previous time point. This action would likely not be considered appropriate by most users, although it gave the least biased results. Naturally, when we choose the method to analyze the data without formal imputation, we tend to use Complete2, which carried the event from the previous time point to the following time points if the observation was missed at this point. This method sounded logical, but unfortunately, it produced a somewhat biased result. Given that the analysis sample size of Complete2 is larger than Complete1, if mean squared error is important, though, the tradeoff between bias and variance may make Complete2 preferred after all.
Currently, in this simulation study, we only focused on random dropout and dropout related to treatment arm. If missing data was related to outcomes or event occurrence, the conclusion might be different. In the future, we might consider increasing the number of time points, or consider the time point that the first missing started to occur.
References
- Heyting A, Tolboom JT, Essers JG. Statistical handling of drop-outs in longitudinal clinical trials. Stat Med. 1992; 11: 2043-2061.
- Shao J, Zhong B. Last observation carry-forward and last observation analysis. Stat Med. 2003; 22: 2429-2441.
- Rubin LH, Witkiewitz K, Andre JS, Reilly S. Methods for Handling Missing Data in the Behavioral Neurosciences: Don't Throw the Baby Rat out with the Bath Water. J Undergrad Neurosci Educ. 2007; 5: A71-77.
- Schneiderman ED, Kowalski CJ, Willis SM. Regression imputation of missing values in longitudinal data sets. Int J Biomed Comput. 1993; 32: 121-133.
- Sterne JA, White IR, Carlin JB, Spratt M, Royston P, Kenward MG, et al. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009; 338: b2393.
- Menzel P, Stadler PF, Gorodkin J. max Alike: Maximum likelihood-based sequence reconstruction with application to improved primer design for unknown sequences. Bioinformatics. 2011; 27: 317-325.
- Bodurtha J, Quillin JM, Tracy KA, Borzelleca J, McClish D, Wilson DB, et al. Mammography screening after risk-tailored messages: The women improving screening through education and risk assessment (WISER) randomized, controlled trial. J Womens Health (Larchmt). 2009; 18: 41-47.
- Liu G, Gould AL. Comparison of alternative strategies for analysis of longitudinal trials with dropouts.J Biopharm Stat. 2002; 12: 207-226.
- Wood AM, White IR, Hillsdon M, Carpenter J. Comparison of imputation and modelling methods in the analysis of a physical activity trial with missing outcomes. Int J Epidemiol. 2005; 34: 89-99.
- Cook RJ, Zeng L, Yi GY. Marginal analysis of incomplete longitudinal binary data: a cautionary note on LOCF imputation. Biometrics. 2004; 60: 820-828.
- Tice JA, Cummings SR, Ziv E, Kerlikowske K. Mammographic breast density and the Gail model for breast cancer risk prediction in a screening population. Breast Cancer Res Treat. 2005; 94: 115-122.