
Special Article - Biostatistics Theory and Methods
Austin Biom and Biostat. 2015;2(3): 1023.
Outcome-Adaptive Allocation using Auxiliary and Primary Outcomes
Sinks S¹, Sabo RT²* and Mukhopadhyay N²
¹Office of Biostatistics, Center for Drug Evaluation and Research, Food and Drug Agency, USA
²Department of Biostatistics, Virginia Commonwealth University, USA
*Corresponding author: Sabo RT, Department of Biostatistics, Virginia Commonwealth University, 830 East Main Street, Richmond, VA 23298-0032, USA
Received: June 01, 2015; Accepted: June 11, 2015; Published: July 02, 2015
Abstract
Studies with delayed outcomes generally receive little benefit from adaptive allocation procedures. In this manuscript we present an optimal design for outcome-adaptive allocation by combining information from delayed primary outcomes and more quickly observed auxiliary outcomes. Bayesian methods are used to construct the joint distribution of these outcomes, which is used to estimate the components of the optimal allocation ratio. Simulation studies show this approach to be effective at achieving adaption even before the delayed outcome is observed.
Keywords: Randomization; Adaptive clinical trials; Study design; Bayesian methods
Introduction
Optimal response-adaptive allocation designs are intended to minimize the overall number of treatment failures observed in a trial. In cases with sufficient evidence of some treatment outperforming another, the allocation algorithm will increase the probability that subjects are allocated to the superior treatment. These designs thus can exhibit fewer treatment failures, then balanced designs [1].
In practice, some primary outcomes – such as survival or relapse – require months or years before they are observed. With these outcomes, there can be a delay in updating the allocation rate for the next patient or group of patients. However, the efficiency of the response adaptive design highly depends on the immediacy of observed data: if few primary end points are observed in early stages of the trial, adaptation will not occur. Bai et al. [2] have shown that moderately delayed responses will not affect asymptotic properties of the adaptive procedure under certain delay mechanisms, though there could be a higher risk of assigning more patients to some inferior treatment. If the rate at which outcomes are observed is too slow relative to the rate of patient accrual, then the benefits of adaptive allocation may not be realized.
In this paper, we introduce an adaptive allocation design that incorporates an auxiliary outcome that is positively correlated with the primary outcome yet is more quickly observed. Rather than use a second outcome as a surrogate or replacement of the primary outcome in the allocation algorithm, our procedure aggregates information from both the auxiliary and primary outcomes, based on the classical response adaptive design framework for binary data. The goals of this paper are to: 1) introduce a response adaptive design framework that simultaneously uses both primary and auxiliary outcomes, and 2) incorporate a bivariate beta distribution [3] as the prior distribution of correlated binomial data to account for dependence between the two outcomes. Relevant background is provided in the next Section, after which the methodological set-up and allocation algorithm are introduced. A simulation study comparing the joint approach with both balanced and optimal allocation is then presented, and the manuscript concludes with a brief discussion.
Materials and Methods
Background
The goal of classical response-adaptive procedures is to minimize the loss function given that the information level at each stage is constant [4]. This loss function contains the difference, in treatment success rates (θ=PA-PB, where PA and PB are the success rates for treatment A and B) and sample size (ni=nA,i+nB,A):
L(θ)=u(θ)nA,i+υ(θ)nB,i (1)
where nA,i and nB,i are the cumulative number of patients assigned to groups A and B at the ith stage of the study, υ(θ) is the loss for a patient allocated to treatment A, and υ(θ) is the loss for a patient allocated to treatment B. We also assume where and are the outcome variance in groups A and B, respectively, and K is some constant.
Patients are generally exposed to two risks in randomized trials: treatment failure and assignment to an inferior treatment. Let θ<0 indicate treatment A is inferior (pA<pB
) and θ>0 indicate treatment B is inferior theta;<0 indicate treatment A is inferior (). The treatment failure risks are described by υ(θ) and υ(θ). The function υ(θ) increases as θ decreases and υ(θ) increases as θ increases. The allocation ratio (nA,i/nB,i) determines the probability of assigning patients to the inferior treatment. The loss function, then integrates these two risks, and our goal is to minimize this loss function subject to the constant variability at each stage of the trial. Minimization of the equation (1) can be solved for the allocation ratio using the delta method (Appendix A.1), and the minimized allocation ratio is:Consequently, we need only model υ(θ)) and υ(θ) to realize some specific objective. For binary response trials, if υ(θ))=υ(θ)=1, the allocation ratio, which is the so-called Neyman allocation rule [5], which minimizes estimator variance. If υ(θ)=1-pA and υ(θ))=1-pB, the allocation ratio A B R = p p turns out to be the socalled optimal allocation ratio, which minimizes the expected number of treatment failures [1]. Loss functions υ(θ and υ(θ can be treated as functions of unknown parameter pA and pB, which can be estimated based on patient responses using a sequential estimation method. If our primary response is delayed, we may not have information to estimate υ(θ), υ(θ) and R appropriately.
Allocation ratio derivation with two outcomes
For treatments j=A or B, suppose Xj is an auxiliary outcome for treatment j and Yj is a primary outcome, where Xj and Yj both are binary variables. According to the observed outcome sequence, we denote PX,j as the “success” rate for the auxiliary outcome in treatment j, and PX,j as the success rate for the primary outcome. We assume that 1) PX,j and PX,j are random variables with some joint distribution, 2) the conditional random variables Xj|PX,j˜BIN(nX,j, PX,j) and Yj|Py,j˜BIN(nY,j,Py,j) are independent, where nX,i and nY,i are the number of observed auxiliary and primary outcomes, and 3) the association between Xjand YJ is explained through the association between PX,j and PX,j Thus, the posterior distribution of PX and PY (we remove the subscripts for simplicity) can be expressed as:As mentioned earlier, u(θ) and υ(θ) are positive functions that measure the risk of assigning patients to treatment A and B given primary efficacies (PY,A,PY,B). In addition, we also have auxiliary efficacies PX,A and PX,B, which offer some information about PY,A and PY,B, respectively, since they are associated. Therefore, it is reasonable to average u(θ) and υ(θ) over all possible sets of PY,A and PY,B given (PX,X,Y)A and (PX,X,Y)B. Based on the loss function (1) of the classical adaptive design framework, the loss function of the procedure using auxiliary and primary outcomes takes the following form:
L(θ)=E[u(θ)|(PX,X,Y)A, (PX,X,Y)B]nA,i +E[υ(θ)|(PX,X,Y)A, (PX,X,Y)B]nB,I (4) where nA,I and nB,i are the number of patients in treatment A and B at ith stage of the trial. The two conditional expectations in (4) can be calculated through the conditional posterior distribution from (3). The minimization of the function (4) is the same as that of the loss function (1) in classical response-adaptive design framework, since the conditional expectations are assumed to be known. Therefore, the allocation ratio is
Two-dimensional beta-binomial model
Martin and Vaeth [6] proposed a two-dimensional beta binomial distribution that can model the association between two count variables. We use a similar approach to model the association between the auxiliary and primary outcomes, which is done through modeling the dependence between their respective success rates. Olkin and Liu [3] derived a bivariate beta distribution from three marginal gamma distributions. We use this distribution as a prior for (PX,j,Py,j). Given the assumptions about the design, the joint distribution of (Xj,Y,j,PX,j,Py,j) is the product of the conditional distributions of Xj|PX,j and Y,j|Py,j and prior distribution of (PX,j,Py,j).
To simplify our notation, the following distributions are generalized to any (X,Y,PX,PY) given a specific treatment.
f(X,Y,PX,PY)=f(X,Y|PX,PY)*f(PX,PY|(α1,α2,β) (5)
Integrating with respect to PY, the joint distribution of (X,Y,PX) is:
*2F1(α1+α2+β;y+α2; α1+α2+β+n2;PX)
Where 2F1 is the Gaussian hyper geometric function. Therefore, the conditional distribution of PY given PX and the data (X,Y) is obtained through division:
f(PY| X,Y,PX)=f(X,Y,PX,PY)/f(X,Y,PX) (7)
As presented in the defined loss function, u(θ) and υ(θ) are functions of PY,A and PY,B. Also, we know that treatment A is independent from treatment B, which indicates the distributions for treatment A (f(X,Y,PX,PY)A) and for treatment B (f(X,Y,PX,PY)A) are independent. As long as we know the conditional distribution (f(PY|X,Y,PX)A) and (f(PY|X,Y,PX)B) for treatment A and B, we are able to calculate the conditional expectation from the loss function (4).
As we are interested only in optimal allocation, we focus solely on the case when u(θ)=1-PY,A and υ(θ) =1-PY,B, recalling that PY,j is the primary efficiency rate in the jth treatment. Then the loss function (4) is reduced to
L(θ)=(1-E[PY,A|( PX,X,Y)A])nA,i+(1-E[PY,B|( PX,X,Y)B])nB,i* (8)
The optimal allocation ratio can then be rewritten as
For a given treatment, the conditional expectation is a function of X,Y,PX with prior parameters (α1,α2,β) (Appendix A.2).
The expression on the right side of equation (9) is the Gauss continued function. The continued function of the Gauss hyper geometric function converges uniformly for 0<PX<1. Therefore, E[PY|X,Y,PX] is guaranteed to reside within the range (0,1). The correlation of X and Y is then proportional to the correlation of PX and PY and takes the following form (Appendix A.3):
Prior density selection
In the beta-binomial model, subject matter expertise can be used to provide some information to assess the probability of having a successful outcome, which then determines the mean or mode of the beta distribution. The sum (r) of a and β determines the variance of the beta distribution given some desired marginal mean. As r increases, the more compact and informative will be the prior distribution. The sum r indicates how confident we are on the expert advice or literature information, and r-2 is known as the effective sample size. If we lack confidence in the prior belief of success probability, we can weigh the data more by selecting a wide unimodal beta density function (i.e. by selecting low r).
For the bivariate beta distribution, we adopt the same logic in selecting the marginal densities, which follow beta distributions. It can be shown that the prior correlation of the Olkin and Liu [3] distribution is narrowly bounded when the marginal means are given, which may diminish the ability of the bivariate prior distribution to adequately model the association between success rates. According to Equation (10), the correlations of auxiliary and primary outcomes is approximately equal to the correlation of auxiliary and primary efficacy as (nx ,ny )» (α1,α2 ,β ) . Therefore, we intend to have a less informative prior by choosing r no greater than 15 when α1, α2 and β are greater than 1. As studied in Olkin and Liu [3], the bivariate beta distribution tends to have a bivariate normal density when α1,α2 and are large.
Estimation rule for allocation rate
Although the allocation rate depends on unknown parameters, we will apply the sequential sampling rule following the trend of optimal adaptive design to update the allocation rate. The prior parameters (α1,α2,β) reveal the knowledge about the correlation between the auxiliary and primary outcomes (X and Y) and efficacies of the outcomes (PX and PY) for a specific treatment. Based on clinician experience or pilot studies, we can determine an appropriate combination of (α1,α2,β) that satisfies and . Let (xk,yk) be the paired auxiliary and primary binary outcomes for the kth subject, and let Tk be that subject’s treatment indicator. Let Iyk indicate whether the primary response for the kth patient has become accessible when a new patient is enrolled in the study. Let F(○)i-1=F((x1,y1,Iy1,T1)…(xi-1,yi-1,Iyi-1,Ti-1)) be the history of the first i – 1 patients. Based on F(○)i-1, then we have the results listed in Table 1.
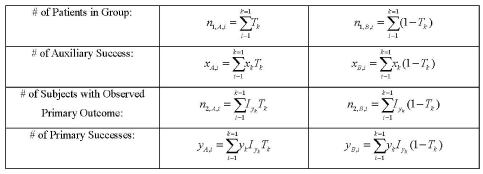
Table 1: Data calculations after ith patient are accrued.
Allocation algorithm
The first two steps in the algorithm for conducting the proposed adaptive design are (1) to set the initial allocation rate to 0.5 for the first patient, and (2) to update the auxiliary efficacy for treatment A and B with posterior means , and for the ith stage. These posterior means are weighted averages of the sample proportion and prior mean, and approximate the sample proportion as the sample size increases. Notice that the posterior distribution of the auxiliary outcome is given by the beta-binomial distribution.
The next step is (3) to calculate R* using, with respect to obtaining estimates of and both posterior means and sample estimates have disadvantages. Posterior variance estimates are functions of the posterior means and are computationally intensive, while sample variances might not be estimable in small sample sizes due to response delays, no events being observed, or patients clustering in one sample. As a compromise, the posterior conditional variance is used for i = k, and the empirical sample variance is used for i > k, where k is the minimum number of accrued patients after which the sample variance is available for both treatment groups. Steps (2) and (3) are then repeated, and randomization is terminated depending on some specified stopping criterion (final sample size achieved, early termination threshold exceeded, etc.).
Results and Discussion
Simulation study sampling methodology
In this simulation study, we are interested in modeling different clinical scenarios to see the performance of our bivariate allocation method compared with both optimal and balanced allocation. Specifically, we examine: 1) how different primary outcomes between treatment A and B affect simulation results, in terms of allocation proportions, the number of patients assigned to each treatment, error rate, number of treatment failures, and 2) how different auxiliary efficacies affect the simulation results.
In many situations, simulations are conducted separately for each method with a large number of repetitions, where each simulated data set represents a single trial. However, this approach could lead to scenarios where one or more of the approaches are exposed to more instances of rarely occurring samples than are other approaches. Thus, it may be more realistic to generate NA random observations from the treatment A population and NB random observations from treatment B population for each trial, where each method would then sample from the same pool of subjects. Suppose N is the total sample size of the clinical trial, then NA and NB should both be greater than N. Within a trial, three allocation methods will actually share the same sample pool to simulate from populations of treatment A and B, and the sample pool is regenerated after each trial. In this manner, we are able to reduce variation between the samples used by each method.
The sample size for balanced allocation is fixed in advance, while the sample size of the adaptive methods is allowed to adjust during the trial. The total sample size for each combination of parameters (discussed below) is selected to yield 90% power for a two-sided Z-test assuming balanced allocation; in cases with no true difference, sample sizes of 100 subjects per group were created. Correlated binomial responses are, sampled from a multinomial distribution given both auxiliary and primary efficacies with a specified correlation [7]; note that this correlation does not vary freely in the range (-1,1) due to restrictions of the joint probability distribution of auxiliary and primary outcomes. We assume the correlation between auxiliary and primary outcomes is fixed regardless of treatment effect.
Simulation settings
Optimal allocation utilizes the primary outcome to update the allocation ratio, which is calculated based on the sample proportions. As mentioned earlier, these sample estimates may not be estimable in early stages of the trial, when no variability exists in treatment responses or no primary responses are available. A lead-in is introduced to the simulation process for optimal allocation during which patients are assigned to treatments with equal probability.
Prior distributions take into account the uncertainty of PX and PY before observed data is considered. Recalling that auxiliary and primary efficacies (PX and PY) follow beta distributions, α1 and β are the shape and scale parameters for the auxiliary efficacy (PX), and α2 and β are the shape parameters for the primary efficacy (PY). We assume that the mean of each prior distribution is equal to some value (pX, pY), which gives us and . Given these two equations, the relationship among (α1, α2, β) can be determined, and with a known correlation between the PX and PY, the exact combination of α1, α2, β) can be found.
Our goal is to model scenarios where the primary outcome has a rare event rate and the auxiliary outcome has a moderate event rate. We thus select primary efficacies between PY∈[0.1,0.3], and auxiliary efficacies between PX∈[0.4,0.7]. Due to restrictions of the correlation in the bivariate beta distribution (see Discussion), we assume the correlation between auxiliary and primary outcomes is 0.5 in all cases. In order to incorporate delayed observations of the primary outcome, we assume the primary outcome for each subject is not observed until 30 additional subjects have accrued into the trial. Alternatively, we assume that the auxiliary outcome is immediately observed.
Simulation results
In what follows, we refer to our proposed method as the bivariate approach and the traditional optimal allocation method as the univariate approach. Table 2 presents the number of patients assigned to treatment B (the more effective treatment) for a given sample size. We first note that in cases of differences in treatment success rates, the bivariate approach accounting for auxiliary information assigns more subjects to the more effective treatment than does the univariate approach. With an effect size of 0.1 between the primary success rates (n = 526), the bivariate optimal method assigned approximately 50 more patients to treatment B than does balanced allocation, while the univariate optimal approach assigned approximately 42 more, which are 19% and 16% improvement over balanced allocation, respectively. When the effect size increases to 0.2 (n = 162), the bivariate approach, allocated on average 23 more patients to treatment B than balanced allocation (a 28% increase), while the univariate approach assigned only 14 more (a 17% increase). We also see that the two adaptive approaches perform similarly to balanced allocation when there is no difference in primary success rates, with the bivariate optimal approach performing similarly even when the auxiliary outcomes have different success rates between treatments.
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
Balance
526
0.1
0.2
0.4
0.7
313.4
304.8
263.5
0.4
0.6
312.2
304.4
262.8
0.5
0.7
312.1
305.0
263.0
0.5
0.6
313.6
305.4
263.2
0.6
0.6
313.0
305.0
263.1
0.4
0.7
104.0
95.4
80.9
0.4
0.6
104.7
96.0
81.1
162
0.1
0.3
0.5
0.7
104.0
95.5
81.1
0.5
0.6
104.8
95.2
80.8
0.6
0.6
104.9
95.4
81.6
0.4
0.6
99.7
99.9
100.3
200
0.3
0.3
0.6
0.5
100.8
100.1
99.8
0.5
0.5
100.0
100.3
99.8
0.7
0.5
97.1
99.9
100.0
Table 2: Summary Number of patients in group B (receiving more effective treatment).
In Table 3 we see the average number of treatment failures for each of the three allocation strategies. Both optimal allocation methods produced slightly fewer failures than balanced allocation, though the improvements were small due to the low success rates for the primary outcomes. In addition, the bivariate approach averaged nearly 1 fewer failure than the univariate approach when the effect size was 0.1 and nearly 2 fewer failures when the effect size was 0.2. While modest (especially compared to the reported standard deviations), this improvement shows that incorporating the more quickly realized auxiliary information in the manner described for the bivariate method can lead to real gains compared to the standard univariate approach. Table 4 shows the estimated empirical power and type-one error rates for each approach. Though the two optimal allocation approaches lead to imbalanced treatment groups, such imbalances did not affect either power or the level of the resulting hypothesis tests.
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
Balance
526
0.1
0.2
0.4
0.7
442.4 (8.6)
443.2 (8.5)
447.3 (7.9)
0.4
0.6
442.1 (8.6)
443.0 (8.5)
447.1 (8.2)
0.5
0.7
441.8 (8.5)
442.5 (8.4)
447.5 (8.1)
0.5
0.6
441.8 (8.9)
442.5 (8.8)
447.3 (8.1)
0.6
0.6
441.2 (8.6)
443.1 (8.7)
447.4 (8.3)
0.4
0.7
125.0 (5.6)
126.7 (5.6)
129.9 (5.0)
0.4
0.6
124.6 (5.5)
126.4 (5.6)
129.5 (5.1)
162
0.1
0.3
0.5
0.7
125.1 (5.4)
126.8 (5.4)
129.5 (5.0)
0.5
0.6
124.8 (5.4)
126.7 (5.3)
129.5 (5.2)
0.6
0.6
124.8 (5.5)
126.6 (5.4)
129.7 (5.2)
0.4
0.6
140.0 (6.8)
140.1 (6.8)
140.2 (6.8)
200
0.3
0.3
0.6
0.5
140.0 (6.4)
140.0 (6.4)
140.0 (6.4)
0.5
0.5
139.8 (6.4)
139.9 (6.3)
139.9 (6.3)
0.7
0.5
139.9 (6.5)
139.9 (6.5)
139.9 (6.4)
Table 3: Summary of Expected Number of Patient Failures (Standard Deviation).
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
Balance
526
0.1
0.2
0.4
0.7
0.92
0.91
0.91
0.4
0.6
0.90
0.92
0.89
0.5
0.7
0.90
0.89
0.92
0.5
0.6
0.91
0.91
0.90
0.6
0.6
0.90
0.90
0.88
0.4
0.7
0.91
0.91
0.91
0.4
0.6
0.91
0.92
0.91
162
0.1
0.3
0.5
0.7
0.90
0.90
0.91
0.5
0.6
0.92
0.92
0.91
0.6
0.6
0.91
0.91
0.91
0.4
0.6
0.06
0.06
0.06
200
0.3
0.3
0.6
0.5
0.05
0.05
0.05
0.5
0.5
0.05
0.05
0.04
0.7
0.5
0.04
0.04
0.05
Table 4: Summary of power/error rate.
Tables 5, 6 and 7 provide estimates of the allocation rates as well as a measure of their variability (Inter quartile Range, IQR) after 25%, 50% and 75% of patients have been accrued. In the low effect size (n = 526) and no difference (n = 200) cases after 25% of the trial has been concluded Table 4, we see that the bivariate and univariate methods have similar average allocation ratios and IQRs. Interestingly, in the large effect size case with a smaller total sample size (n = 162), we see that the univariate approach has not yet begun adapting, since few primary outcomes have been observed at this point. These results show that while the bivariate and univariate allocation approaches behave similarly after enough observations are in hand, the ability of the bivariate approach to begin the adaptation sooner is the determining factor in any gains it exhibits over the univariate approach. We see that the allocation ratios and their variability’s did not change much after 50% (Table 6) and 75% (Table 7) of the patients are accrued. At this point both the bivariate and univariate procedures allocate patients between treatments in almost identical manners, regardless of effect size.
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
526
0.1
0.2
0.4
0.7
0.41 (0.36, 0.45)
0.41 (0.37, 0.45)
0.4
0.6
0.41 (0.36, 0.46)
0.41 (0.36, 0.46)
0.5
0.7
0.41 (0.36, 0.46)
0.41 (0.37, 0.46)
0.5
0.6
0.41 (0.37, 0.45)
0.41 (0.37, 0.45)
0.6
0.6
0.41 (0.36, 0.45)
0.41 (0.37, 0.45)
0.4
0.7
0.34 (0.32, 0.37)
0.50 (0.50, 0.50)
0.4
0.6
0.33 (0.32, 0.36)
0.50 (0.50, 0.50)
162
0.1
0.3
0.5
0.7
0.33 (0.32, 0.37)
0.50 (0.50, 0.50)
0.5
0.6
0.33 (0.31, 0.36)
0.50 (0.50, 0.50)
0.6
0.6
0.33 (0.31, 0.35)
0.50 (0.50, 0.50)
0.4
0.6
0.50 (0.46, 0.54)
0.50 (0.45, 0.55)
200
0.3
0.3
0.6
0.5
0.50 (0.46, 0.54)
0.50 (0.45, 0.55)
0.5
0.5
0.50 (0.47, 0.53)
0.50 (0.45, 0.55)
0.7
0.5
0.51 (0.46, 0.55)
0.50 (0.45, 0.55)
Table 5: Summary of Allocation Rate (IQR) at the 25th percentile visit for treatment A.
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
526
0.1
0.2
0.4
0.7
0.41 (0.38, 0.44)
0.41 (0.38, 0.44)
0.4
0.6
0.41 (0.38, 0.44)
0.41 (0.38, 0.44)
0.5
0.7
0.41 (0.36, 0.44)
0.41 (0.38, 0.44)
0.5
0.6
0.41 (0.36, 0.44)
0.41 (0.38, 0.44)
0.6
0.6
0.41 (0.36, 0.44)
0.41 (0.38, 0.44)
0.4
0.7
0.35 (0.32, 0.41)
0.38 (0.32, 0.44)
0.4
0.6
0.35 (0.32, 0.41)
0.37 (0.32, 0.43)
162
0.1
0.3
0.5
0.7
0.36 (0.32, 0.41)
0.38 (0.32, 0.43)
0.5
0.6
0.36 (0.32, 0.41)
0.38 (0.32, 0.44)
0.6
0.6
0.36 (0.32, 0.41)
0.38 (0.32, 0.43)
0.4
0.6
0.50 (0.47, 0.53)
0.50 (0.47, 0.53)
200
0.3
0.3
0.6
0.5
0.50 (0.47, 0.53)
0.50 (0.47, 0.53)
0.5
0.5
0.50 (0.47, 0.53)
0.50 (0.47, 0.53)
0.7
0.5
0.51 (0.47, 0.53)
0.50 (0.47, 0.53)
Table 6: Summary of Allocation Rate (IQR) at the 50th percentile visit for treatment A.
Sample
Size
Primary
Auxiliary
Method
TRT A
TRT B
TRT A
TRT B
Bivariate
Univariate
526
0.1
0.2
0.4
0.7
0.41 (0.39, 0.43)
0.41 (0.39, 0.43)
0.4
0.6
0.41 (0.39, 0.43)
0.41 (0.39, 0.43)
0.5
0.7
0.41 (0.39, 0.43)
0.41 (0.39, 0.43)
0.5
0.6
0.42 (0.39, 0.44)
0.42 (0.39, 0.44)
0.6
0.6
0.41 (0.39, 0.44)
0.41 (0.39, 0.44)
0.4
0.7
0.36 (0.32, 0.40)
0.36 (0.31, 0.40)
0.4
0.6
0.36 (0.32, 0.40)
0.36 (0.31, 0.40)
162
0.1
0.3
0.5
0.7
0.36 (0.32, 0.40)
0.36 (0.32, 0.40)
0.5
0.6
0.36 (0.31, 0.40)
0.36 (0.32, 0.40)
0.6
0.6
0.36 (0.31, 0.40)
0.36 (0.32, 0.41)
0.4
0.6
0.50 (0.48, 0.52)
0.50 (0.48, 0.53)
200
0.3
0.3
0.6
0.5
0.50 (0.48, 0.52)
0.50 (0.47, 0.52)
0.5
0.5
0.50 (0.48, 0.52)
0.50 (0.48, 0.52)
0.7
0.5
0.50 (0.48, 0.52)
0.50 (0.48, 0.53)
Table 7: Summary of Allocation Rate (IQR) at the 75th percentile visit for treatment A.
Conclusion
In this manuscript we introduced an optimal allocation strategy for reducing binary treatment failures when the primary outcome is delayed in measurement. Our approach compliments the lagged primary outcome with a quickly observed auxiliary binary outcome, assuming that both outcomes are positively correlated. The information from both outcomes is combined using a Bayesian approach, where we use a bivariate beta prior to model the dependence between the success rates of the primary and auxiliary outcomes. We have shown the dependence between the rates to be proportional to the dependence between primary and auxiliary observations. This Bayesian approach also allows researchers to incorporate information from other sources, including results from previous studies, pilot data, or even hypotheses based on clinical expertise.
One limitation of the presented work is that we only considered trials with two groups. While optimal allocation designs exist for three-group trials [8], the allocation rations are more complex, and have not been expressed in closed form for any case greater than three groups [8,9]. Our focus was also solely upon binary outcomes. We have assumed that the auxiliary and primary outcomes are known to be positively correlated a priori. Hence we did not study scenarios where the correlation between the two outcomes was positive, but weak (we assumed a correlation of 0.5), where there was no correlation, or where the correlation was negative.
Natural extensions of this approach would be to account for more than two groups, and also to account for continuous outcomes, or even cases where primary and auxiliary outcomes are of different modeling types (e.g., continuous and discrete). The loss-function approach used in Sections 2 and 3 could be used again to find the bivariate optimal allocation ratio for cases of three or more treatment arms, as Jeon and Hu [8] derived the univariate optimal allocation ratio for minimizing treatment failures in trials with three arms and binary outcomes. A similar approach could be used to jointly model continuous primary and auxiliary outcomes, though incorporating the association between such outcomes with a bivariate normal distribution will be more straightforward than the current approach. Jointly modeling heterogeneous modeling types can follow the general outline provided here, though selecting a bivariate prior distribution may become more challenging.
The choice of modeling the association between primary and auxiliary outcomes through modeling the association between primary and auxiliary success rates with prior information was done for simplicity. We selected the bivariate beta distribution for this prior [3], though other distributions can certainly be used. An alternative approach would be to jointly model the outcomes in a way that directly incorporates their dependence, which would then allow separate prior elicitation for the marginal parameters of each outcome. In cases where we are interested in either different prior specification or in jointly modeling the outcomes, copula functions offer flexible alternatives.
Acknowledgement
We are grateful for the support and encouragement provided by Dr. Karl Peace. Services in support of the research project were generated by the VCU Massey Cancer Center Biostatistics Shared Resource, supported, in part, with funding from NIH-NCI Cancer Center Support Grant P30 CA016059.
References
- Rosenberger WF, Stallard N, Ivanova A, Harper CN, Ricks ML. Optimal adaptive designs for binary response trials. Biometrics. 2001; 57: 909-913.
- Bai ZD, Hu F, Rosenberger WF. Asymptotic properties of adaptive designs for clinical trials with delayed response. The Annals of Statistics. 2002; 30: 122-139.
- Olkin I, Liu R. A bivariate beta distribution. Statistics and Probability Letters. 2003; 62: 407-412.
- Jennison C, Turnball BW. Group Sequential Methods With Applications to Clinical Trials. Chapman and Hall/CRC. 2000.
- Melfi V, Page C. Variability in adaptive designs for estimation of success probabilities. Lecture Notes-Monograph Series. 1998; 34: 106-114.
- Martin BB, Vaeth M. The two-dimensional beta binomial distribution. Statistics and Probability Letters. 2011; 81: 884-891.
- Haynes ME, Sabo RT, Chaganty NR. Simulating dependent binary variables through multinomial sampling. Journal of Statistical Computation and Simulation. 2015; in press.
- Jeon Y, Hu F. Optimal adaptive designs for binary response trials with three treatments. Statistics in Biopharmaceutical Research. 2010; 2: 310-318.
- Tymofyeyev Y, Rosenberger WF, Hu F. Implementing optimal allocation in sequential binary response experiments. Journal of the American Statistical Association. 2007; 102: 224-234.