
Research Article
Austin Biom and Biostat. 2016; 3(1): 1032.
A Note on the Required Sample Size of Model-Based Dose-Finding Methods for Molecularly Targeted Agents
Sato H1*†, Hirakawa A2*† and Hamada C3
1Biostatistics Group, Center for Product Evaluation, Pharmaceuticals and Medical Devices Agency, Japan
2Statistical Analysis Section, Center for Advanced Medicine and Clinical Research, Nagoya University Hospital, Japan
3Department of Information and Computer Technology, Tokyo University of Science, Japan †These authors contributed equally to this work.
*Corresponding author: Sato H, Biostatistics Group, Center for Product Evaluation, Pharmaceuticals and Medical Devices Agency, 3-3-2 Kasumigaseki, Chiyodaku, Tokyo 100-0013, Japan
Received: November 07, 2016; Accepted: December 05, 2016; Published: December 14, 2016
Abstract
Some Molecularly Targeted Agents (MTAs) exhibit non-monotonic patterns in the dose-response relationships. Although many model-based dose-finding methods to account for such patterns have been proposed, the required sample size to determine the true Optimal Dose (OD) has not been adequately investigated. A little knowledge of the required sample size might potentially prevent wide-ranging application of model-based dose-finding methods in practice. In this study, we focus on three model-based dose-finding methods that accommodate non-monotonic patterns in the dose-efficacy relationship, and discuss the required sample sizes under various conditions, using simulation studies. We found that the selection rate of the true OD did not necessarily improve as the sample size increased. Based on the results of our simulation studies, we provide notes and guidelines on sample size determination when using model-based dose-finding methods for MTAs.
Keywords: Change-point model; Sample size; Dose-finding; Oncology; Phase I
Abbreviations
AR: Adaptive Randomization; CP: Change Point; CP method: dose-finding method proposed by Sato et al.; CRM: Continual Reassessment Method; MCMC: Markov Chain Monte Carlo; MTD: Maximum Tolerated Dose; MTAs: Molecularly Targeted Agents; OD: Optimal Dose; TC method: dose-finding method proposed by Thall and Cook; WMD: Weighted Mahalanobis Distance; WT method: dose-finding method proposed by Wages and Tait
Introduction
The objective of phase I oncology trials is generally to determine the Maximum Tolerated Dose (MTD). This is defined as the highest dose level that can be administered to patients with clinically acceptable toxicity. The dose-finding methods for determining the MTD are roughly categorized into two groups, model-based and rule-based methods. Rule-based methods, such as the 3+3 design, are widely used in practice, but the lack of statistical rationale and low accuracy of determining the true MTD are often problematic. Many model-based dose-finding methods, such as the Continual Reassessment Method (CRM) [1], assume that the probabilities of toxicity and efficacy of an agent increase monotonically as the dose of the agent increases; therefore, dose escalation or de-escalation is commonly based solely on toxicity outcome. Such methods outperform rule-based methods in many cases [2-4].
Some Molecularly Targeted Agents (MTAs) exhibit nonmonotonic patterns in dose-efficacy relationships. Therefore, the model-based dose-finding method based on the above-mentioned assumptions may not be reasonable for determining the Optimal Dose (OD) of MTAs. To account for non-monotonic patterns in the dose-efficacy relationships of MTAs, dose-finding methods that account for both toxicity and efficacy outcomes are required. Such methods generally determine the OD based on toxicity and efficacy outcomes. The OD is often considered to be the dose level with the maximum efficacy probability among the dose levels with toxicity probabilities lower than a pre-specified value (e.g., 30 or 40%), although the definition of the OD varies depending on the individual method proposed. Many researchers have developed dose-finding methods based on toxicity and efficacy outcomes for single-agent or two-agent combination phase I trials [5-11]. Thall and Cook [6] proposed using the Gumbel model [12] to capture the relationship between the bivariate binary toxicity and efficacy outcomes (termed the TC method). They used a quadratic model for the dose-efficacy relationship in order to consider a non-monotonic pattern. Wages and Tait [11] proposed using a power model for the binary efficacy and toxicity outcomes (termed the WT method). They assumed some class of working model for the efficacy outcome and used model selection techniques to allow greater flexibility in modeling the doseefficacy relationship. Recently, we developed a new dose-finding method using the Change-Point (CP) logistic model for single MTA trials (termed the CP method) [13]. Specifically, we developed a doseefficacy model, the parameters of which are allowed to change in the vicinity of the change point of the dose level, in order to address non-monotonic patterns of the dose-efficacy relationship. The change point is defined as the dose that maximizes the log-likelihood of the assumed dose-efficacy and dose-toxicity models.
Although many useful dose-finding methods have been proposed that account for non-monotonic patterns of the dose-efficacy relationship for MTAs, the required sample size for determining true the OD using these methods has not been adequately investigated. For instance, the selection rate for the true OD is generally evaluated using fixed sample sizes in simulation studies [6,11,13], but the required sample size to achieve the target selection rate for the true OD is not. Thus, little is known about the required sample size for the existing dose-finding methods for MTA. It is useful for investigators to provide the required sample sizes to use novel model-based dosefinding methods under various conditions (e.g., number of dose levels evaluated and prior distribution for model parameters). In this study, we focus on the three model-based dose-finding methods that can be used for MTA (i.e., the CP, TC, and WT methods), and discuss the required sample size to determine the true OD under various conditions, using simulation studies. Based on the results of the simulation studies, we provide notes and guidelines for determining the sample size for model-based dose-finding methods for MTAs.
This paper is organized as follows: in the next section, we provide an overview of the three dose-finding methods. The simulation studies are described in the third section, and we discuss the determination of the required sample size and provide guidelines for determining the sample size for model-based dose-finding methods for MTAs in the fourth section.
Dose-Finding Methods Used
An adaptive dose-finding method for a MTA using the Change-Point model (CP method)
Let YEi and YTi denote binary efficacy and toxicity outcomes for the ith of N patients, respectively. YEi(orYTi)= 1 indicates that efficacy (or toxicity) is observed, and YEi(orYTi) = 0 otherwise. Following Islam et al. [14], the joint probabilities for YEi and YTi are given in Table 1.
YTi
0
1
YEi
0
p00
p01
1-pE
1
p10
p11
pE
1-pT
pT
1
Table 1: The joint probabilities for YEi and YTi.
To model the toxicity outcomes, the bivariate joint probability function for YEi and YTi is factorized into the conditional probability of toxicity given an efficacy outcome Pr(YTi= k| YEi= j; k,j = 0,1) and the marginal probability of efficacy Pr(YEi= j; j = 0,1) as follows:
where
yi00 = (1-yEi)(1-yTi), j=0, k=0,
yi01 = (1-yEi)yTi, j=0, k=1,
yi10 = yEi(1-yTi), j=1, k=0, and
yi11 = yEiyTi, j=1, k=1.
The conditional probability functions of toxicity given each efficacy outcome are modeled by an ordinary logistic model, that is,
and
where xi={d1,…,dL} is an actual dose of the agent administered to the ith patient, θ0= {a0,β0} and θ1= {a1,β1} are unknown parameters for the models in Equations (2) and (3), respectively. Given the actual dose dl(l=1,…,L), we consider the standardized dose It should be noted that these conditional models are equal (i.e., θ0= θ1) under independence of efficacy and toxicity [14].
Next, we propose a CP logistic model for modeling the marginal probability function for efficacy, as follows:
where d* is the change point of the dose between and θE={aE,βE} and are unknown parameters.
For the current data of n patients Dn, we calculate the likelihoods under the assumptions of respectively, that is where In the Bayesian inference for θl, we assume that the prior distribution for each parameter f(θl) is an independent normal distribution, although other distributions can be used. For each Ln,l(l=1,…,L-1), the posterior distribution of θl is given by Using the Markov chain Monte Carlo (MCMC) method, we obtain the posterior mean ∧θ l for each θl.
Owing to the ease of use, we used the method of Rukhin [15] to determine the change point. Given the posterior mean, we determine the estimated change point ofthat provides the maximum value among,that is,
Dose allocation algorithm in the CP method: To stabilize the parameter estimations for θl and d* at an early stage of the trial, we incorporate the run-in period when the first cohort of patients is treated at the lowest dose level and escalate the dose level unless more than or equal to two of three patients in that cohort experience toxicity. A cohort consists of three patients throughout.
After the run-in period, we start the model-based dose-finding stage. Using the estimated change point ofand the corresponding posterior means of we calculate the posterior probabilities of efficacy and toxicity outcomes for each dose which are denoted asrespectively. To avoid allocating ineffective or severely toxic dose levels, we determine the set of acceptable doses based on these probabilities, as follows [6]:
where cE and cT are the respective critical values for the posterior probabilities of efficacy and toxicity outcomes, and dE and dT are fixed probability cutoffs. That is, we extract the doses that are expected to be effective and not severely toxic at a certain level.
Among the doses we select the dose that is allocated to the next cohort of patients based on the Weighted Mahalanobis Distance (WMD) proposed by Hirakawa [8]. We obtain the kth posterior samples, which are generated by the MCMC method, of the WMD of the outcome to the optimal point (1,0):
where
and wE and wT are the prespecified weight parameters for adjusting the trade-off between efficacy and toxicity, respectively. Denote the correlation coefficient described in Islam et al. [14].
The posterior mean of the WMD is given by averaging the posterior samples, that is,
The dose with the minimum value of among is allocated to the next cohort of patients. If there is no acceptable dose at an interim time point, then the trial is terminated at that time point and no dose is selected as the OD. Otherwise, we apply this algorithm until reaching the maximum sample size and then select the dose allocated to the next cohort of patients as the OD.
Dose-finding based on efficacy-toxicity trade-offs (TC method)
Thall and Cook [6] formulate the marginal probability of toxicity pT(d',θT) and efficacy pE(d',θE) as follows:
where θT=(μT,βT) and θE=(μE,βE,1,βE,2) are unknown parameters. They propose using a Gumbel model [12] in the form of:
pa,b=Pr(YE=a,YT=b|d',θ)
for a,b∈{0,1} and the association parameter Ψ. Thus, θ=(μT,βT,μE,βE,1,βE,2,Ψ).
Denoting the data for the first n patients in the trial as Dn, they calculate the likelihood Ln(Dn|θ). They assume each component θq of θ is normally distributed, with mean and standard deviation Let denote the vector of hyperparameters, with all prior covariance set equal to 0, and let φ(θ|ξ) denote the multivariate normal prior of θ. To compute posteriors, they numerically integrate Ln(Dn|θ)φ(θ|ξ) with respect to θ using the method of Monahan and Genz [16].
Dose-finding algorithm in the TC method: The first cohort is treated at the starting dose specified by the physician. They define the set of acceptable doses based on the probabilities shown in Equation (6). For each subsequent cohort, satisfies Equation (6), or if is the lowest untried dose above the starting dose and it satisfies Pr then
The dose-finding algorithm is based on explicit trade-offs between pE and pT. They construct a target efficacy-toxicity trade-off contour, C, by fitting a curve to target values of that the physician considers equally desirable. Once C is established, they use it to define the desirability of any pair of probabilities as follows. Draw a straight line, Line(q), from q to (1, 0), to find the point p where Line (q) intersects C. Calculate the Euclidean distances ρ(p) from p to (1, 0), and ρ(q) from q to (1, 0). To reflect the fact that values of q closer to (1, 0) are more desirable, they define the desirability of q to be D(q)=ρ(p)/ρ(q)-1.
If then the trial is terminated and no dose is selected. Otherwise, the dose that maximizes D(q) is selected among the doses subject to the constraint that no untried dose may be skipped when escalating. This algorithm is applied until the maximum sample size is reached.
Model-selecting dose-finding method (WT method)
Wages and Tait [11] formulate the marginal probability of toxicity where 0 < q1 < … < qL < 1 are standardized units (the skeleton) representing discrete dose levels dl, l=1,…,L. At the same time, they make use of some classes of working models and model selection techniques in order to allow for more flexibility in modeling the dose-efficacy relationship. They specify K = 2 × L - 1 working models; L unimodal skeletons, with nodes at each of the L doses, and L - 1 plateau skeletons, with nodes at each of the first L - 1 doses. For a particular skeleton, k; k=1,…,K, they model the marginal probability of efficacy for a class of working dose-efficacy models and ∈θ. Here, 0<p1k<…<pLk<1 is the skeleton of model k. Further, they account for any prior information concerning the plausibility of each model, and so introduce Pr(Modelk) such that
They estimate the parameters β and θ based on the Bayesian framework. For the current dataof n patients Dn, to estimate the parameter β, they calculate the likelihood L(β|Dn), and utilize a normal prior distribution g(β). For L(β|Dn), the posterior distribution of β is given by g(β|Dn)∝g(β)L(β|Dn). To estimate the parameter θ, the likelihood under model k is given by Lk(θ|Dn), and utilizes a normal prior h(θ). Given the set Dn and the likelihood, the posterior density for θ is given by hk(θ|Dn)∝h(θ)Lk(θ|Dn). This information can be used to establish posterior model probabilities given the data as
The prior model probabilities, Pr(Modelk), are updated with the efficacy data. Each time a new patient is to be enrolled, they choose a single skeleton, k*, with the largest posterior probability such that
k*=arg maxk PMP(Modelk), (15)
They then utilize to generate efficacy probability estimates at each dose. Beginning with the prior for θ and having included the jth subject, they can compute the posterior probability of a response for dl so that
Dose-finding algorithm in the WT method: Overall, each enrolled patient is allocated the dose estimated to be the most efficacious, among those with acceptable toxicity. In general, after n enrolled patients, they define the set of acceptable doses as
where øT is the maximum acceptable toxicity rate.
Early in the trial, they do not rely entirely on the maximization of estimated efficacy probabilities for guidance as to the most appropriate treatment but rather implement Adaptive Randomization (AR) to obtain broader information. Based on the estimated efficacy probabilities, for doses in An, a randomization probability Rl is calculated:
and the next patient or cohort of patients is randomized to dose dl with probability Rl. They rely on this randomization algorithm for the subset of nR patients. Further, the starting dose with a probability Rl is chosen based on the starting skeleton, k*, for efficacy.
Upon completion of the AR phase, the trial design switches to a maximization phase, in which maximized efficacy probability estimates guide allocation. Among the doses contained in An, they allocate the (n + 1) th patient cohort to the dose xn+1 according to the estimated efficacy probabilities, pE(dl), such that
If the stopping rules (the details can be found in Wages and Tait [11]) take effect at an interim time point, then the trial is terminated at that time point and no dose is selected as the OD. Otherwise, this algorithm is continued until the maximum sample size is reached.
Simulation Studies
Common settings for the three dose-finding methods
We considered two actual dose sets in a single-agent dosefinding trial: six actual doses dl={1,2,3,4,5,6} and four actual doses dl={1,2,3,4}. Given these actual doses, the standardized doses were for the six actual doses, and for the four actual doses [6]. The starting dose was set as the lowest dose
We investigated the ten different scenarios with respect to the true probabilities of efficacy and toxicity for the dose levels, (Table 2). The dose-efficacy and dosetoxicity relationships based on are shown in Figure 1. In each scenario, the conditional probabilities had to be specified and were calculated by substituting true into the following equations, although these are not shown in this paper:
Dose level
1
2
3
4
5
6
Scenario 1
pT,pE
0.05, 0.05
0.10, 0.20
0.15, 0.35
0.20, 0.50
0.25, 0.45
0.30, 0.40
WMD
4.50
2.14
1.54
1.23
1.37
1.53
Trade-off value
-0.22
-0.03
0.17
0.35
0.28
0.21
Scenario 2
pT,pE
0.05, 0.05
0.10, 0.15
0.15, 0.25
0.25, 0.60
0.45, 0.65
0.65, 0.70
WMD
4.50
2.52
1.90
1.11
1.30
1.66
Trade-off value
-0.22
-0.09
0.04
0.46
0.37
0.15
Scenario 3
,

0.05, 0.05
0.10, 0.25
0.15, 0.50
0.20, 0.45
0.25, 0.40
0.30, 0.35
WMD
4.50
1.87
1.18
1.33
1.48
1.66
Trade-off value
-0.22
0.04
0.36
0.29
0.22
0.15
Scenario 4
,

0.05, 0.05
0.15, 0.30
0.25, 0.55
0.35, 0.57
0.45, 0.59
0.55, 0.61
WMD
4.50
1.70
1.19
1.27
1.37
1.52
Trade-off value
-0.22
0.10
0.41
0.39
0.33
0.24
Scenario 5
pT,pE
0.05, 0.30
0.15, 0.70
0.25, 0.60
0.35, 0.50
0.45, 0.40
0.55, 0.30
WMD
1.62
0.86
1.11
1.38
1.70
2.10
Trade-off value
0.10
0.61
0.46
0.31
0.16
0.01
Scenario 6
pT,pE
0.05, 0.30
0.08, 0.68
0.22, 0.70
0.35, 0.72
0.55, 0.74
0.75, 0.76
WMD
1.62
0.82
0.94
1.08
1.38
1.96
Trade-off value
0.10
0.59
0.58
0.50
0.28
0.03
Scenario 7
,

0.05, 0.05
0.10, 0.30
0.15, 0.50
0.20, 0.80
WMD
4.50
1.66
1.18
0.79
Trade-off value
-0.22
0.10
0.36
0.69
Scenario 8
pT,pE
0.05, 0.05
0.10, 0.30
0.30, 0.55
0.80, 0.65
WMD
4.50
1.66
1.24
2.31
Trade-off value
-0.22
0.10
0.39
-0.04
Scenario 9
pT,pE
0.05, 0.25
0.15, 0.65
0.40, 0.50
0.65, 0.10
WMD
1.83
0.93
1.44
3.61
Trade-off value
0.04
0.55
0.29
-0.24
Scenario 10
pT,pE
0.05, 0.25
0.20, 0.65
0.50, 0.68
0.80, 0.71
WMD
1.83
0.99
1.35
2.26
Trade-off value
0.04
0.54
0.33
-0.03
Table 2: True values of (pT, pE), Weighted Mahalanobis Distance (WMD), and trade-off value for each dose level. The OD is shown in bold.
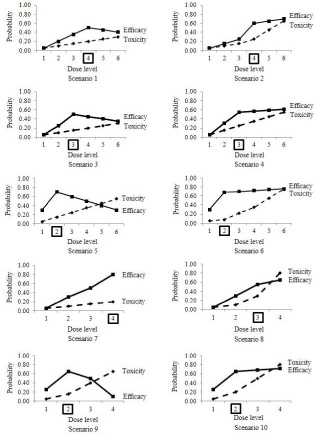
Figure 1: Ten simulation scenarios. The Optimal Dose (OD) is indicated by the dose level enclosed in a square.
Using the ten scenarios, we assessed the selection rates of the true OD given a sample size N of 36, 48, 60, and 72 for scenarios 1-6, and 24, 30, 36, and 42 for scenarios 7-10. The number of patients allocated to each dose level was set to 3. Each simulation study consisted of 1,000 trials.
Settings for the CP method
We used the PROC MCMC procedure in SAS, version 9.3 (SAS Institute Inc., Cary, NC, USA) to obtain the posterior distributions of parameters. The method for the specification of hyper parameters for the prior normal distribution
was described by Sato et al. [13]. We considered six sets of prior efficacy and toxicity probabilities of dose levels (Table 3) and a correlation coefficient of Ψ1=Ψ=0.20 (see Equation (9) in Sato et al. [13]) to generate the mean of the prior normal distribution for all hyper parameters for the prior normal distribution. The standard deviation values were commonly set to 3.0. Using these values, we evaluated the effects of the hyper parameters for the prior normal distribution (Table 4) on the selection rate for the true OD of the CP method.
Setting
d1
d2
d3
d4
d5
d6
1
(0.05, 0.05)
(0.10, 0.20)
(0.15, 0.35)
(0.20, 0.50)
(0.25, 0.55)
(0.30, 0.60)
2
(0.05, 0.30)
(0.10, 0.70)
(0.15, 0.60)
(0.20, 0.50)
(0.25, 0.40)
(0.30, 0.30)
3
(0.05, 0.05)
(0.10, 0.20)
(0.15, 0.35)
(0.20, 0.50)
(0.25, 0.65)
(0.30, 0.80)
4
(0.05, 0.05)
(0.15, 0.25)
(0.25, 0.40)
(0.35, 0.55)
5
(0.05, 0.30)
(0.15, 0.70)
(0.25, 0.50)
(0.35, 0.30)
6
(0.05, 0.05)
(0.15, 0.50)
(0.25, 0.55)
(0.35, 0.60)
Table 3: The prior toxicity and efficacy probabilities (q1,p1).
Prior setting
Mean
?








1
-2.191
0.936
-0.951
0.353
-0.599
2.114
-0.375
1.123
3.0
2
-2.662
1.800
-1.160
1.005
0.274
0.732
-0.833
0.546
3.0
3
-2.315
0.717
-0.983
0.298
-0.736
2.308
-0.736
2.308
3.0
4
-1.535
1.483
-0.554
0.630
-0.024
2.663
-0.410
2.107
3.0
5
-1.732
2.141
-0.604
1.416
1.834
2.445
0.006
-2.945
3.0
6
-1.700
0.603
-0.672
1.432
1.714
4.248
0.199
0.712
3.0
Table 4: Mean and standard deviation of the prior normal distribution in the CP method.
The weight parameters wE and wT for the WMD were set to 1.0. The value of the true WMD shown in Table 2 was obtained by substituting true into Equations (8) and (9), and into Equation (7). The critical values for the posterior probabilities of efficacy and toxicity cE and cT were set to 0.20 and 0.40, respectively, and fixed probability cutoffs dE and dT were both set to 0.10.
Settings for the TC method
We used the publically released software "EffTox" (version 4.0.12), downloaded from https://biostatistics.mdanderson.org/ SoftwareDownload/Default.aspx. Using the EffTox software, we achieved a fair comparison between the three methods (the details can be found in Sato et al. [13]). The hyper parameters of the prior distribution with respect to the model parameters were automatically calculated depending on prior efficacy and toxicity probabilities (Table 3) and effective sample size. Effective sample size was set to 0.90 based on the recommendation of the software developer. EffTox requires specification of a trade-off value, which was termed the "desirability parameter" in the original paper by Thall and Cook [6]. We set
to obtain the equalized Euclidean distance from the respective points on the trade-off contour to the point of (1, 0) and obtained the true trade-off value shown in Table 2 by inputting the true into the EffTox software. The critical values for the posterior probabilities of efficacy and toxicity cE and cT were set to 0.20 and 0.40, respectively, and fixed probability cutoffs dE and dT were both set to 0.10.
Settings for the WT method
We used the R code released at https://faculty.virginia. edu/model-based_dose-finding/Wages%20and%20Tait%20 R%20code. R to perform the WT method. We set the skeleton values for the marginal probability of toxicity q=(q1,q2,q3,q4,q5 ,q6)=(0.01,0.08,0.15,0.22,0.29,0.36) for scenarios 1-6, and q=(q1,q 2,q3,q4)=(0.05,0.15,0.25,0.35) for scenarios 7-10. In scenarios 1-6, we set eleven skeletons for the marginal probability of efficacy pk=(p1k,p2k,p3k,p4k,p5k,p6k), k=1,…,11 as follows:
p1=(0.60,0.50,0.40,0.30,0.20,0.10),
p2=(0.50,0.60,0.50,0.40,0.30,0.20),
p3=(0.40,0.50,0.60,0.50,0.40,0.30),
p4=(0.30,0.40,0.50,0.60,0.50,0.40),
p5=(0.20,0.30,0.40,0.50,0.60,0.50),
p6=(0.10,0.20,0.30,0.40,0.50,0.60),
p7=(0.20,0.30,0.40,0.50,0.60,0.60),
p8=(0.30,0.40,0.50,0.60,0.60,0.60),
p9=(0.40,0.50,0.60,0.60,0.60,0.60),
p10=(0.50,0.60,0.60,0.60,0.60,0.60), and
p11=(0.60,0.60,0.60,0.60,0.60,0.60).
Additionally, in scenarios 7-10, we set seven skeletons pk=(p1k,p2k,p3k,p4k), k=1,…,7 as follows:
p1=(0.60,0.45,0.30,0.15),
p2=(0.45,0.60,0.45,0.30),
p3=(0.30,0.45,0.60,0.45),
p4=(0.15,0.30,0.45,0.60),
p5=(0.30,0.45,0.60,0.60),
p6=(0.45,0.60,0.60,0.60), and
p7=(0.60,0.60,0.60,0.60).
We assumed that each of these models was equally likely and set Pr(Modelk)= 1/11 in scenarios 1-6, and Pr(Modelk)= 1/7 in scenarios 7-10. We set the normal prior distribution g(β) and h(θ) with mean0 and variance 1.34 as prior settings 1 and 4, with mean0 and variance 3 as prior settings 2 and 5, and with mean0 and variance 0.5 as prior settings 3 and 6. The size of the adaptive randomization phase was set equal to half of the maximum sample size. The critical values for the posterior probabilities of efficacy and toxicity cE and cT were set to 0.20 and 0.40, respectively.
Simulation results
Table 5 shows the selection rates for the true OD of each dosefinding method for each prior setting under scenarios 1-6 with six dose levels, which are displayed in Figure 2. As shown in Figure 2, the selection rates for true OD of the three methods were almost constant, irrespective of the prior settings. Across prior settings 1-3, the average increase in the selection rate for the true OD when the sample size was increased from 36 to 72 was 5.6%, -0.3%, and 4.5% for the CP, TC, and WT methods, respectively. In the TC and WT methods, the selection rate for the true OD decreased as the sample size increased in some cases. In scenario 2, in which the probabilities of toxicity and efficacy of an agent roughly and monotonically increase as the dose of the agent increases, the average increase in the selection rate for the true OD when the sample size was increased from 36 to 72 was 11.7%, 7.7%, and 8.0% for the CP, TC, and WT methods, respectively.
Prior setting 1
Prior setting 2
Prior setting 3
N
36
48
60
72
36
48
60
72
36
48
60
72
Scenario 1
CP
39
39
42
44
37
42
40
45
35
38
41
40
TC
9
7
5
5
10
7
7
7
9
8
5
4
WT
38
45
47
50
35
45
44
51
40
46
51
51
Scenario 2
CP
55
63
62
65
59
64
66
71
52
57
61
65
TC
44
51
50
53
52
56
58
62
47
50
46
51
WT
44
43
46
50
37
42
45
49
44
48
48
50
Scenario 3
CP
41
43
46
44
44
50
48
52
36
38
42
43
TC
2
2
2
2
5
4
3
3
3
2
2
1
WT
41
44
50
49
46
48
49
52
41
41
46
48
Scenario 4
CP
47
49
50
51
49
50
52
52
41
45
42
46
TC
25
22
24
23
28
26
29
26
24
25
21
23
WT
46
44
46
48
43
46
46
46
46
43
45
48
Scenario 5
CP
64
63
67
70
69
65
69
73
64
61
63
63
TC
24
23
26
24
25
28
28
26
24
24
25
24
WT
69
68
70
72
65
65
67
69
67
71
68
74
Scenario 6
CP
49
51
50
52
52
52
56
54
49
49
50
53
TC
13
12
11
11
14
14
14
11
13
11
11
10
WT
40
35
35
34
39
34
30
32
45
39
36
34
Table 5: The selection rate (%) of the true OD in Scenarios 1-6.
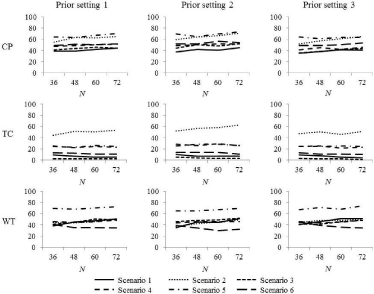
Figure 2: The selection rate of the true OD in scenarios 1-6.
Table 6 shows the selection rates for the true OD of each dosefinding method for each prior setting under scenarios 7-10 with four dose levels, which are displayed in Figure 3. The selection rate for the true OD of the three methods increased slightly as the sample size increased. Across prior settings 5-7, the average increase in the selection rate for the true OD when the sample size was increased from 24 to 42 was 5.3%, 7.3%, and 9.5% for the CP, TC, and WT methods, respectively. For all three methods, the magnitude of the increase in the selection rate for the true OD as the sample size increased was similar, irrespective of prior settings and scenarios 7-10.
Prior setting 4
Prior setting 5
Prior setting 6
N
24
30
36
42
24
30
36
42
24
30
36
42
Scenario 7
CP
82
83
84
87
62
62
63
68
74
74
77
75
TC
86
89
90
91
83
86
89
90
85
85
91
91
WT
64
65
69
74
59
61
64
69
66
71
75
80
Scenario 8
CP
74
77
82
82
74
74
76
79
83
78
91
80
TC
88
92
93
95
88
91
94
94
89
92
93
95
WT
71
75
78
82
65
69
73
78
75
78
83
84
Scenario 9
CP
72
74
77
78
79
80
82
84
76
78
78
81
TC
44
48
48
51
47
52
52
55
46
46
47
54
WT
79
83
87
89
77
83
86
88
80
86
87
88
Scenario 10
CP
74
77
82
84
78
83
85
85
77
83
83
85
TC
68
71
75
78
73
76
81
80
70
77
76
80
WT
73
73
77
77
73
75
76
78
72
76
77
81
Table 6: The selection rate (%) of the true OD in Scenarios 7-10.
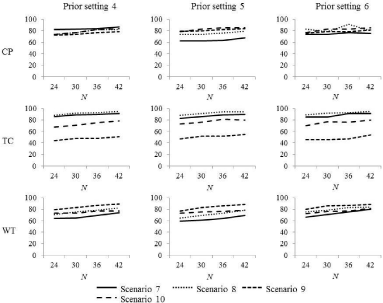
Figure 3: The selection rate of the true OD in scenarios 7-10.
Discussion
In this study, we assessed the relationship between the selection rate for the true OD and sample size in three model-based dosefinding methods that account for a non-monotonic pattern of doseefficacy curve, using simulation studies. According to the report of Le Tourneau et al. [17], the sample sizes used in phase I trials evaluating four and six dose levels are 20-30 and 40-50, respectively. We, therefore, evaluated the selection rate for the true OD of the three methods using sample sizes of 24-42 for the scenarios with four dose levels, and of 36-72 for the scenarios with six dose levels.
The simulation studies revealed several important findings with respect to the relationship between the selection rate for the true OD and sample size. First, the selection rate for the true OD did not substantially improve as the sample size increased when the number of dose levels was six, even if the sample size was doubled. The selection rate for the true OD in the best-performing method under each scenario was 50-70% at maximum when the sample size ranged from 36-72. This result may suggest that the model-based dose-finding methods we used in this study cannot capture the complex dose-efficacy and dose-toxicity curves using a sample size that is feasible for phase I trials. The development of new dose-finding methods is warranted in order to address this issue. Furthermore, such findings were also observed when the number of dose levels was five (result not shown).
Second, the selection rate for the true OD improved as the sample size increased when the number of dose levels was four. We could maintain the selection rate for the true OD at approximately 80% by using the best-performing method under each scenario in many cases. The best-performing method for selecting the true OD was the TC method in scenarios 7 and 8, the WT method in scenario 9, and the CP method in scenario 10; therefore, the performance of each method varied depending on the scenario. It is therefore important to carefully assume the possible dose-efficacy and dose-toxicity curves of the investigational MTA before beginning the trial.
Third, the prior distribution to be assumed for the model parameters of each method did not impact the above-mentioned findings. This would be a desirable operating characteristic of the model-based dose-finding method based on the Bayesian theorem, although it should be fine-tuned through a simulation study before conducting the trial, so that the dose-finding method used provides optimal performance for selecting the true OD in practice.
Conclusion
In conclusion, when planning the phase I dose-finding trial for a single MTA, we recommend attempting to reduce the number of dose levels, based on data available for the investigational MTA, such as pre-clinical data. When evaluating four dose levels of a single MTA, the three model-based dose-finding methods we evaluated in this study would provide better performance for selecting the true OD for the phase I trial, using a feasible sample size. However, to determine the OD among five or more dose levels, the operating characteristics of the dose-finding method should be carefully examined in a simulation study before beginning the trial.
Funding Statement
This work was partially supported by JSPS KAKENHI [Grant Number 15K15948] (Grant-in-Aid for Young Scientists B). The views expressed herein are the result of independent work and do not necessarily represent the views of the Pharmaceuticals and Medical Devices Agency.
References
- O'Quigley J, Pepe M, Fisher L. Continual reassessment method: a practical design for phase I clinical trials in cancer. Biometrics. 1990; 46: 33-48.
- Goodman SN, Zahurak ML, Piantadosi S. Some practical improvements in the continual reassessment method for phase I studies. Stat Med. 1995; 14: 1149-1161.
- Ahn C. An evaluation of phase I cancer clinical trial designs. Stat Med. 1998; 17: 1537-1549.
- Iasonos A, Wilton AS, Riedel ER, Seshan VE, Spriggs DR. A comprehensive comparison of the continual reassessment method to the standard 3+3 dose escalation scheme in phase I dose-finding studies. Clin Trials. 2008; 5: 465-477.
- Braun TM. The bivariate continual reassessment method: extending the CRM to phase I trials of two competing outcomes. Control Clin Trials. 2002; 23: 240-256.
- Thall PF, Cook JD. Dose-finding based on efficacy-toxicity trade-offs. Biometrics. 2004; 60: 684-693.
- Bekele BN, Shen Y. A Bayesian approach to jointly modeling toxicity and biomarker expression in a phase I/II dose-finding trial. Biometrics. 2005; 61: 344-354.
- Hirakawa A. An adaptive dose-finding approach for correlated bivariate binary and continuous outcomes in phase I oncology trials. StatMed. 2012; 31: 516-532.
- Asakawa T, Hamada C. A pragmatic dose-finding approach using short-term surrogate efficacy outcomes to evaluate binary efficacy and toxicity outcomes in phase I cancer clinical trials. Pharm Stat. 2013; 12: 315-327.
- Asakawa T, Hirakawa A, Hamada C. Bayesian model averaging continual reassessment method for bivariate binary efficacy and toxicity outcomes in phase I oncology trials. J Biopharm Stat. 2014; 24: 310-325.
- Wages NA, Tait C. Seamless phase I/II adaptive design for oncology trials of molecularly targeted agents. J Biopharm Stat. 2015; 25: 903-920.
- Murtaugh PA, Fisher LD. Bivariate binary models of efficacy and toxicity in dose-ranging trials. Commun Stat A-Theor. 1990; 19: 2003-2020.
- Sato H, Hirakawa A, Hamada C. An adaptive dose-finding method using a change-point model for molecularly targeted agents in phase I trials. Stat Med. 2016; 35: 4093-4109.
- Islam MA, Chowdhury RI, Briollais L. A bivariate binary model for testing dependence in outcomes. Bull Malaysian Math Sci Soc. 2012; 35: 845-858.
- Rukhin AL. Asymptotic behavior of estimators of the change-point in a binomial probability. J Appl StatSci. 1995; 1: 1-12.
- Monahan J, Genz A. Spherical-radial integration rules for Bayesian computation. J Am Stat Assoc. 1997; 92: 664-674.
- Le Tourneau C, Lee JJ, Siu LL. Dose escalation methods in phase I cancer clinical trials. J Natl Cancer Inst. 2009; 101: 708-720.