Modeling the Number of COVID-19 Confirmed Cases and Deaths in Puerto Rico: One-year Experience

Suarez EL; Reyes JC; Mattei H; Lopez-Cepero A; Perez CM

Research Article

Austin Biom and Biostat. 2021; 6(1): 1038.

Modeling the Number of COVID-19 Confirmed Cases and Deaths in Puerto Rico: One-year Experience

Suarez EL¹*, Reyes JC¹, Mattei H², Lopez-Cepero A³ and Perez CM¹

¹Department of Biostatistics and Epidemiology, Graduate School of Public Health, University of Puerto Rico, San Juan, Puerto Rico

²Department of Social Sciences, Graduate School of Public Health, University of Puerto Rico, San Juan, Puerto Rico

³Department of Nutrition, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, USA

*Corresponding author: Suarez EL, Department of Biostatistics and Epidemiology, Graduate school of Public Health, Medical Sciences Campus, University of Puerto Rico, P.O. Box 365067, San Juan, Puerto Rico 00936- 5067

Received: April 02, 2020; Accepted: April 23, 2021; Published: April 30, 2021

Abstract

Aims: To describe and project the number of COVID-19 cases and deaths reported in Puerto Rico, according to age and sex.

Methods: We used surveillance data from March 8, 2020 to March 13, 2021 to describe and predict, by age and sex, the number of cases and deaths in Puerto Rico using Generalized Additive Models. The statistical modeling was performed in R software using the mgcv package.

Results: The analytic sample consisted of 95,208 confirmed cases and 2,080 deaths reported by the Puerto Rico Department of Health until the second week of March 2021. The risk of COVID-19 infection was highest among adults aged 20-59 years, as compared with those younger than 20 years (RR_{20-39 vs. <20}: 2.35 [95% CI: 1.80-3.06] and (RR_20-59 _vs._<20: 2.30 [95% CI: 1.76-3.00]). However, the pattern in the risk of death showed an inverse relationship: the highest risk of death occurred in adults 60 years and over as compared with those younger than 60 years (RR_{≥80 vs. <60}: 22.4 [95% CI: 18.9-26.5] and (RR_{60-79 vs. <60}: 6.7 [95% CI: 5.6-7.9]). Although there were no significant differences in the risk of infection (p>0.1) by sex, males had a 70% (95% CI: 50-100%) greater risk of death than their female counterparts. The projected weekly number of confirmed cases of COVID-19 showed a downward trend; we expected approximately 510 confirmed cases of COVID-19 in the week ending March 27, 2021. Similarly, the projected weekly number of COVID-19 deaths showed a downward trend.

Conclusion: Future studies are needed to understand age and sex differences in COVID-19 infections and deaths. Increments in the number of COVID-19 cases in the short term are of great concern to justify more substantial preventive restrictions.

Keywords: COVID-19; Predictions; GAM; Puerto rico

Abbreviations

COVID-19: Coronavirus Disease 19; SARS-CoV-2: Severe Acute Respiratory Syndrome Coronavirus 2; RR: Relative Risk; CI: Confidence Interval; GAM: Generalized Additive Models; EDF: Effective Degrees of Freedom

Introduction

Coronavirus disease, COVID-19, is a highly infectious condition caused by the severe acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2). As of March 30, 2021, the COVID-19 pandemic has resulted in over 128 million confirmed cases globally, of which nearly 2.8 million patients have died [1]. The United States of America (USA) is the world’s hardest-hit country, reaching more than 30 million COVID-19 cases and more than 550,000 deaths. In Puerto Rico, an unincorporated territory of the USA, the first confirmed cases of COVID-19 were identified between March 9-13, 2020 [2]. As of March 16, 2021, 95,330 confirmed cases and 2,085 deaths had been reported by the Puerto Rico Department of Health [3]. This epidemic has worsened the ongoing crises (i.e., financial crisis and aftermath of Hurricanes Irma and María and ongoing earthquakes) by creating parallel pandemics that exacerbate socioeconomic standing and residents' health [4]. Poverty may also worsen these challenges, with rates exceeding 43% [5] and debilitating the healthcare infrastructure [6]. Moreover, individuals residing in Puerto Rico have a significant burden of chronic conditions (i.e., obesity and type 2 diabetes) [7,8], putting them at higher risk of COVID-19 complications.

The exponential growth of COVID-19 cases, which fluctuates according to government restrictions, warrants the need to assessing its real burden of COVID-19. This information is critical to ensure adequate medical care and public health resources and mitigate adverse disease outcomes. The high numbers of COVID-19 cases threaten to disrupt healthcare systems further, resulting in severe reductions in health service delivery to detect other diseases [9-11]. Statistical modeling represents an excellent tool to assess the number of future COVID-19 cases, spatial and temporal dynamics of the infection, and evaluate public health interventions' effects. Generalized Additive Models (GAM) can model complex non-linear relationships when there are many predictors. Thus, GAMs are ideal for studying COVID-19 cases and deaths to control the observed fluctuations due to government restrictions at different time points. Using surveillance data collected in Puerto Rico, the present study's objective was to project the number of COVID-19 cases and deaths at two-weeks and estimate the risks of infection and death by age and sex in this vulnerable population.

Materials and Methods

The data on COVID-19 cases and deaths were extracted from the Puerto Rico Health Department Surveillance System, including age, sex, and municipality of residence [12]. People who were not residents in Puerto Rico at the time of infection or death or who had incomplete demographic data were excluded from analyses. The historical period to describe and project the weekly confirmed COVID-19 cases and deaths started on the week ending March 14, 2020 (week 11) and finished on week ending March 13, 2021 (week 63). The data was summarized by epidemiologic week that begins on a Sunday and ends on a Saturday.

To reach the aims of this study, we initially assumed that the weekly number of confirmed COVID-19 cases followed a Poisson distribution [13]; thus, the basic model for the projections was based on the following expression:

log(µ_i) = log(P_i) + Sex_j + Age_k + f(t)

where:

μ_i indicates the expected number of confirmed COVID-19 cases in the i-th week.

P_i indicates the estimated population in the i-th week.

log(P_i) is an offset parameter.

Sex_j indicates the sex effect when males are compared to females.

Age_k indicates the age effect when k-th group is compared with the reference age group.

f(t) indicates a function of t (unit of time measured in weeks), which is a nonparametric function.

To obtain weekly population estimates for the analysis period, we interpolated the annual population estimates by age, sex, and municipality produced by the US Census (2020) for Puerto Rico with a cubic Hermite piecewise interpolation using the STATA command pchipolate [14]. Since the most recent estimate available was for July 1, 2019, we projected the total population to July 1, 2021, assuming the average population change observed two years before Hurricane María (2015 to 2017) would resume in 2019. The age and sex projected populations were obtained by maintaining their distributions and applying them to the projected population.

The purpose of f(t) in GAM is to control the trend and periodicity of a characteristic of interest (seasonality). GAM is a type of regression spline because it could divide the predictors' range of values into different regions, which are identified by different cut points called knots. The parameter estimation in GAM is based on minimizing the following expression:

λ is a non-constant or tuning parameter.

When using GAM, the assumption of linearity between predictors and response variable is relaxed. Categorical predictors, interactions terms, and probability distributions other than normal can be used. Additionally, mixed approaches can include autocorrelation estimates or hierarchical sampling structures. The definition of different time points determines the flexibility of the fit with GAM (identified by t^*) under the following function:

where m+1 is called the order of the spline (the default value is m=2). The function B_j^m (t_i) is identified as B-spline and is a recursive function defined as follows:

β_j is the coefficient for the j^th knot that increases or decreases the function B_j^m (t).

To choose the model that best fits the data, the Generalized Cross-Validation (GCV) score is computed by comparing the observed and the expected values as follows [15]:

where A is the influence matrix and denotes the prediction of μ_i obtained from the model fitted to all data except for the observation y_i. A better model is the one with the smallest ν_g.

To estimate the expected number of confirmed cases of COVID-19, we fitted the historical data of confirmed COVID-19 cases with GAM, including age and sex as categorical predictors, and the smooth term for weeks by age and sex; in addition, the natural log of the mid-year population estimates for 2020 by age and sex was included as an offset variable. Based on our a priori hypothesis that the expected number of confirmed COVID-19 cases and deaths vary by age and sex, we evaluated the age-sex interaction term. Since this interaction term was not statistically significant (p>0.05) based upon a likelihood ratio test, we did not include the interaction term between age and sex in our final models.

We used the function gam with the library mgcv in the R software to fit this model, combining several options to obtain the best fit. We used the option of corrAR1 to account for temporal autocorrelations. We used the option penalized-spline (ps), which constructs a base-model with a subsample of the original database and then uses the base-model to fit the final model. We determined the number of knots based on the lowest values of the GCV using the options k=-1 available in the gam function. For the risk of infection, the quasipoisson option in the probability distribution of the outcome was used due to the observed overdispersion after examining the closeness of the model's deviance to the degrees of freedom; however, for mortality risk, we used the option poisson because no overdispersion was observed. The model's variance was estimated using the Restricted Maximum Likelihood as a bias-reducing alternative to maximum likelihood. The previous modeling procedures were also performed for COVID-19 deaths. The Akaike Information Criterion (AIC) and Schwarz’s Bayesian Information Criterion (BIC) were also used to compare and assess the models' fitness performance. The gam.check function in R was used to generate standard diagnostic plots (Q-Q plots and scatter plots) to examine the residuals' distribution. Running GAM in the library mgcv provides an estimation of the Effective Degrees of Freedom (EDF), according to the stratification required (e.g., age group and sex categories), to have an approximation of the overall trend of the data using a polynomial model [14].

To describe the magnitude of the association between the demographic characteristics (age and sex) and COVID-19 infection in Puerto Rico, we estimated the age-specific rates as follows [15]:

The annual population estimates for Puerto Rico were obtained from the Population Division of the US Census Bureau [16]. Then, we compared the rates of COVID-19 infection in different age groups, estimating the Relative Risk (RR) with 95% confidence intervals based on the parameters’ estimation of GAM, as follows:

where se(Age_k) indicates the standard error of the age-effect under GAM.

A RR_{j vs k} > 1.0 indicates that the risk of infection in in the j^th age group is greater than the k^th age group's risk. A indicates that the risk of infection in the j^th age group is lower than in the k^th age group.

A similar procedure was performed to compare the risk of death due to COVID-19 by demographic characteristics. The reference categories for modeling COVID-19 risks of infection and death were age groups <20 years and ≤60 years, respectively. Afterward, based on the same model, the weekly number of infected individuals and fatalities due to COVID-19 was projected. All statistical modeling was performed in R software version 2.14.1 [17], and the graphs were made in Stata (v. 16).

Table 1: R-programming and output for confirmed COVID-19 cases.




  
    Model specifications: m1 =    gam(cases ~fage + fsex + s (t, bs="ps", k=-1, by=fage: fsex) +    offset (log (pop)), fam = quasipoisson, data = data1, corr = corAR1(form =    ~t))
  
  
    Parametric coefficients
  
  
    
    Estimate
    Std. Error
    t value
    Pr (>|t|)
  
  
    (Intercept)
    -8.73641
    0.12753
    -68.507
    <    2e-16***
  
  
    fage2
    0.85299
    0.13497
    6.32
    6.58e-10***
  
  
    fage3
    0.83025
    0.13427
    6.184
    1.46e-09***
  
  
    fage4
    0.35526
    0.13912
    2.554
    0.0110*
  
  
    fage5
    0.28919
    0.16664
    1.735
    0.0834
  
  
    fsex2
    -0.0137
    0.05589
    -0.245
    0.8064
  
  
    Approximate significance of smooth terms
  
  
    
    edf
    Ref.df
    F
    p-value
  
  
    s(t):fage:fsex1:1
    8.871
    8.983
    32.41
    <2e-16***
  
  
    s(t):fage:fsex1:2
    8.925
    8.993
    36.07
    <2e-16***
  
  
    s(t):fage:fsex2:1
    8.934
    8.996
    77.11
    <2e-16***
  
  
    s(t):fage:fsex2:2
    8.96
    8.998
    89.19
    <2e-16***
  
  
    s(t):fage:fsex3:1
    8.963
    8.999
    69.98
    <2e-16***
  
  
    s(t):fage:fsex3:2
    8.945
    8.997
    80.58
    <2e-16***
  
  
    s(t):fage:fsex4:1
    8.905
    8.993
    38.35
    <2e-16***
  
  
    s(t):fage:fsex4:2
    8.879
    8.988
    44.2
    <2e-16***
  
  
    s(t):fage:fsex5:1
    5.845
    6.55
    12.21
    1.71e-13***
  
  
    s(t):fage:fsex5:2
    5.754
    6.476
    14.99
    <2e-16***
  
  
    Signif. Codes: 0 ‘^***’ 0.001 ‘^**’ 0.01 ‘^*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq. (adj.) = 0.927; Deviance explained = 94.5%; GCV = 13.222; Scale est. = 10.277; n = 517.



Table 1: R-programming and output for confirmed COVID-19 cases.

Results

The total number of confirmed COVID-19 cases and deaths reported by the Puerto Rico Department of Health until the second week of March 2021 was 95,330 and 2,085, respectively. However, for this analysis, we only included confirmed cases and deaths within the period from March 8, 2020, to March 13, 2021, to have the most reliable data due to the observed delay in reporting COVID-19 cases and deaths. After excluding people who did not have complete demographic characteristics, the analytical samples of cases and deaths were 95,208 and 2,080, respectively. Among confirmed cases, women accounted for more than half (53.6%), and 33.8% were aged between 20 and 49 years (median=40 years, IQR= [25,56]). In contrast, 57.3% of deaths were men, and 81.7% were 60 years or older (median=74 years, IQR= [64, 83]). Nearly 30% of the cases lived in the metropolitan health region (San Juan, Guaynabo, Carolina, Trujillo Alto, Canóvanas, and Loíza) (data are not shown).

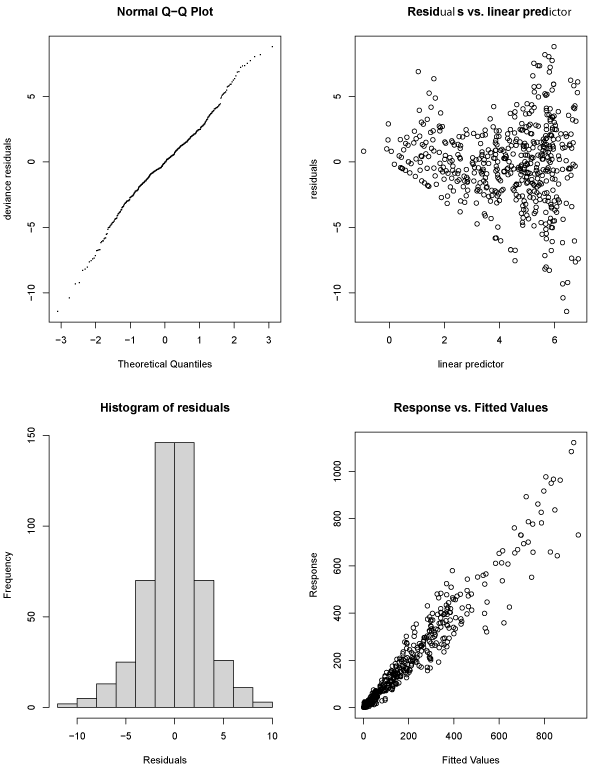
Figure 1: Residual analysis (output) for modeling the weekly number of confirmed COVID-19 cases.

    
    
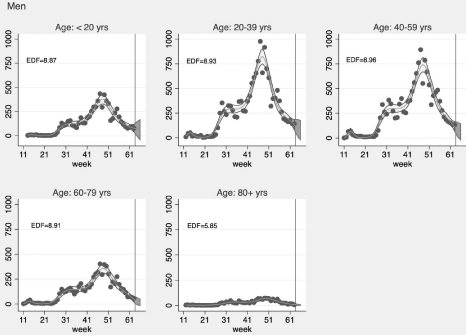
    Figure 1: Residual analysis (output) for modeling the weekly number of confirmed COVID-19 cases.

Figure 2: Weekly number of confirmed COVID-19 cases in Puerto Rico by age among men. Dots correspond to the number of confirmed cases from March 8, 2020 (week 11) to March 13, 2021 (week 63). The period of projection (grey area) was from March 14, 2021 (week 64) to March 27, 2021 (week 65). The solid lines correspond to the 95% confidence intervals.

    
    
    Figure 2: Weekly number of confirmed COVID-19 cases in Puerto Rico by age among men. Dots correspond to the number of confirmed cases from March 8,
2020 (week 11) to March 13, 2021 (week 63). The period of projection (grey area) was from March 14, 2021 (week 64) to March 27, 2021 (week 65). The solid
lines correspond to the 95% confidence intervals.

Confirmed COVID-19 cases

The expected number of confirmed COVID-19 cases in Puerto Rico differed significantly (p<0.05) across all age groups; however, there were no statistical differences by sex (p>0.05) (Table 1). Although the interaction terms between age group and sex in this model were not significant (p>0.05), the EDFs showed that not all trend patterns by age group and sex were the same (p<0.05). The residuals’ analyses showed a symmetrical distribution around zero, but there was a rising trend in the residuals when the estimates of the linear predictor values increased (Figure 1).

While men and women had the same risk of COVID-19 infection, there were significant differences across age groups (Table 2). Compared with the youngest age group (<20 years), individuals aged 20-39 years (RR: 2.35, 95% CI: 1.80-3.06), 40-59 years (RR: 2.3, 95% CI: 1.76-2.99), and 60-79 years (RR: 1.43, 95% CI: 1.09, 1.87) had a significant higher risk of COVID-19 infection after adjusting for sex, population size, and week smoother.

The projections of the expected number of confirmed COVID-19 cases by age group and sex, using GAM, showed marked upward trends among individuals aged 20-79 years, especially those aged 20-59 years, compared to the trends observed in other age groups in both men (Figure 2) and women (Figure 3). The predicted cases by age group and sex for the week ending the 27 of march 2021 (week=65), based on the GAM model, were as follows: (1) <20 years: 65 (95% CI: 0, 159) among men and 59 (95% CI: 0, 143) among women, (2) 20-39 years: 90 (95% CI: 0, 187) among men and 99 (95% CI: 0, 201) among women; (3) 40-59 years: 74 (95% CI: 0, 156) among men and 69 (95% CI: 0, 145) among women; (4) 60-79 years: 23 (95% CI: 0, 62) among men and 19 (95% CI: 0, 49) among women; (5) ≥80 years: 5 (95% CI: 0, 15) among men and 6 (95% CI: 0, 15) among women.

COVID-19 deaths

Before estimating the expected number of COVID-19 deaths in Puerto Rico, age was regrouped into three categories (<60 years, 60-79 years, ≥80 years). The GAM output for expected deaths showed significant results (p<0.05) across age groups and sex categories (Table 3). The EDFs related to the trend in the number of deaths by age group and sex showed significant results (p<0.05). Analyses of the residuals showed an approximately symmetrical distribution around zero, and the deviance residuals were close to the line of theoretical quantiles using the normal distribution (Figure 4).

Table 2: Risk of COVID-19 infection by age and sex: March to December 2020.







Predictor


Category


Cases
(n=95,208)


Estimated Population^*
(n=3,131,564)


Rate
(x 100,000)


RR_crude
(95% CI)^†


RR_adjusted
(95% CI)^‡




Sex


Men


44,153


1,486,234


2,970.80


1


1




Women


51,055


1,645,330


3,103.00


1.05 (0.97, 1.12)


0.99 (0.88, 1.10)




Age (years)


<20


14,111


646,692


2,182.00


1


1




20-39


32,162


795,373


4,043.60


1.85 (1.74, 1.97)


2.35 (1.80, 3.06)




40-59


30,260


818,003


3,699.30


1.70 (1.60, 1.81)


2.30 (1.76, 2.99)




60-79


15,343


693,193


2,213.40


1.02 (0.94, 1.09)


1.43 (1.09, 1.87)




³80


3,332


178,303


1,868.70


0.86 (0.76, 0.97)


1.34 (0.96, 1.85)

^*Population estimated at mid-year 2020.

^†Using the Poisson model when adjusting for population size and the smoother of week.

^‡Using the Poisson model when adjusting for age (or sex), population size, and week smoother. No significant interaction terms were shown in the model (p>0.05).



Table 2: Risk of COVID-19 infection by age and sex: March to December 2020.

Table 3: R-programming and output for COVID-19 deaths.




  
    m1 = gam (deaths ~fage + fsex + s (t,    bs = "ps", k=-1, by = fsex: fage) + offset (log (pop)), fam = poisson;    data = data1; corr = corAR1 (form = ~t), method = "REML").
  
  
    Formula: deaths ~ fage + fsex +    s(t, bs = "ps", k = -1, by = fsex:fage) + offset(log(pop)).
  
  
    Parametric coefficients
  
  
    
    Estimate
    Std. Error
    Z value
    Pr(>|Z|)
  
  
    (Intercept)
    -12.43216
    0.06376
    -194.995
    <2e-16***
  
  
    fage2
    1.99942
    0.07299
    27.394
    <2e-16***
  
  
    fage3
    3.13453
    0.07484
    41.883
    <2e-16***
  
  
    fsex2
    -0.47883
    0.05663
    -8.455
    <2e-16***
  
  
    Approximate significance of smooth terms
  
  
    
    edf
    Ref.df
    Chi.sq
    p-value
  
  
    s(t):fsex:fage1:1
    4.935
    5.761
    73.96
    8.4e-14***
  
  
    s(t):fsex:fage1:2
    7.607
    8.198
    246.57
    <    2e-16***
  
  
    s(t):fsex:fage1:3
    6.484
    7.086
    153.43
    <    2e-16***
  
  
    s(t):fsex:fage2:1
    3.275
    3.941
    19.46
    0.000497***
  
  
    s(t):fsex:fage2:2
    6.3
    7.02
    115.74
    <    2e-16***
  
  
    s(t):fsex:fage2:3
    5.87
    6.607
    129.75
    <2e-16***
  
  
    Signif. Codes: 0 ‘^***’ 0.001 ‘^**’ 0.01 ‘^*’ 0.05 ‘.’ 0.1 ‘ ’ 1;
R-sq. (adj.) = 0.775; Deviance explained = 93.7%; REML = 702.39; Scale est. = 1; n = 280.



Table 3: R-programming and output for COVID-19 deaths.

Table 4: Risk of COVID-19 deaths by age group and sex: March to December 2020.







Predictor


Strata


Deaths


Population


Rate (x100,000)


RR_crude(95% CI)


RR_adjusted(95% CI)^*




Sex


Men


848


1,486,234


57.1


1.5 (1.4, 1.7)


1.7 (1.5, 2.0)




Women


612


1,645,330


37.2


1.0


1.0




Age in years


³80


511


178303


286.6


22.6 (19.5, 26.1)


22.4 (18.9, 26.5)




60-79


668


693,193


99.3


7.7 (6.7, 8.9)


6.7 (5.6, 7.9)




<60


281


2,260,068


12.4


1.0


1.0

^*Using a Poisson regression model adjusting for sex (or age), week smoother, and population size at mid-year 2020. No significant interaction terms were shown in this model (p>0.05).



Table 4: Risk of COVID-19 deaths by age group and sex: March to December 2020.

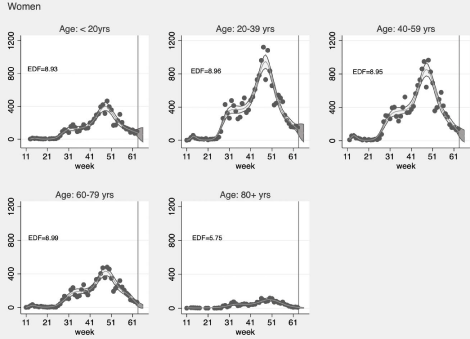
Figure 3: Weekly number of confirmed COVID-19 cases in Puerto Rico by age among women. Dots correspond to the number of confirmed cases from March 8, 2020 (week 11) to March 13, 2021 (week 63). The period of projection (grey area) was from March 14, 2021 (week 64) to March 27, 2021(week 65). The solid lines correspond to the 95% confidence intervals.

    
    
    Figure 3: Weekly number of confirmed COVID-19 cases in Puerto Rico by age among women. Dots correspond to the number of confirmed cases from March
8, 2020 (week 11) to March 13, 2021 (week 63). The period of projection (grey area) was from March 14, 2021 (week 64) to March 27, 2021(week 65). The solid
lines correspond to the 95% confidence intervals.

Figure 4: Residual analysis (output) for modeling the weekly number of COVID-19 deaths.

    
    
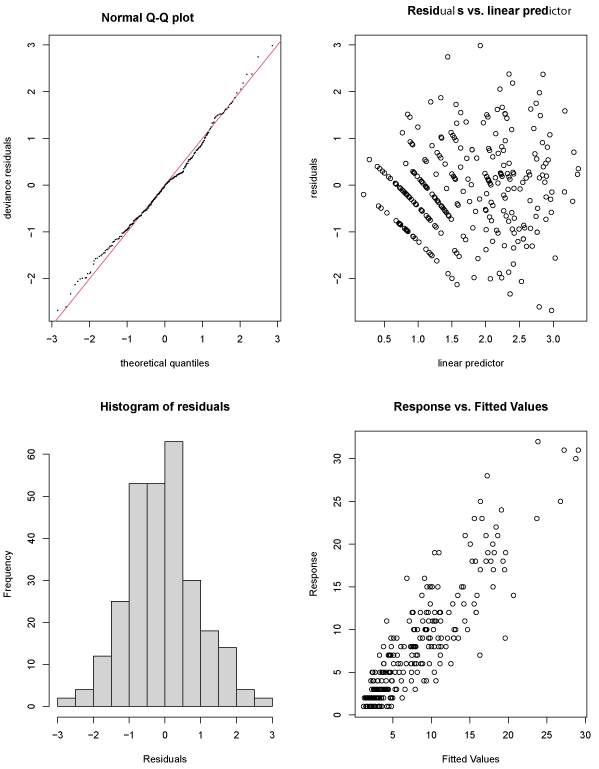
    Figure 4: Residual analysis (output) for modeling the weekly number of COVID-19 deaths.

After adjusting for sex, population size, and the week smoother, men had a 1.7 (95% CI: 1.5, 2.0) times greater risk of death than women (Table 4). Compared to those aged <60 years, the risk of death in people aged 60-79 years was 6.7 (95% CI: 5.6-7.9) times higher and even greater risk for those aged ≥80 years were (RR_{≥80 vs. <60}: 22.4 (95% CI: 18.9, 26.5)).

When we projected the number of deaths for the week ending March 27, 2021 (week=65), a substantial reduction is expected in all age groups in both sexes compared with the reported number of deaths by mid-December of year 2020 (Figure 5). The predicted number of deaths due to COVID-19, by age group and sex, for the week ending the 27 of March 2021 (week=65), based on the GAM model, were as follows: (1) <60 years: 1 (95% CI: 0, 2) among men and 2 (95% CI: 0, 3) among women, 2 60-79 years: (95% CI: 0, 5) among men and 3 (95% CI: 0, 6) among women; (3) ≥80 years: 1 (95% CI: 0, 2) among men and 1 (95% CI: 0, 2) among women.

Discussion

This study documents a higher risk of infection of COVID-19 among young adults and a higher risk of deaths among elderly adults in Puerto Rico, confirming reports from the PR Department of Health. Our results did not find differences by sex in the risk of infection, but it documented a higher risk of death in men than women. Lastly, our study demonstrated a substantial reduction in the number of confirmed cases and deaths due to COVID-19 by the end of March 2021. For week 65 (March 21-27, 2021), a 53% reduction in the number of cases is expected compared with the average number of cases for the first two weeks of March 2021. For week 65 (March 21-27, 2021), a 50% reduction in deaths is expected compared with the average number of deaths for the first two weeks of March 2021.

Our finding on younger age being a risk factor for COVID-19 infection and older age for death from COVID-19 agrees with previous studies [18-20]. For example, a population-wide cohort study on 233,566 residents of Ontario, Canada, reported that individuals younger than 60 years had a death rate of 0.4% (for women) and 0.6% (for men), whereas this rate significantly increased in individuals of 60-79 years to 7.8% (in women) and 12.8% (in men), and in individuals over 80 years (24.9% in women and 34.6% in men) [21]. Another study in the USA documented that adults of younger age contribute more to the number of COVID-19 cases than adults of older age [19]. The percent contribution to COVID-19 infections was 41% for individuals aged 35-49 years and 34.7% for those aged 20-34 years, whereas these estimates were 15.3% for 50-64 years, 2.5% for 65-79 years, and 0.3% for those over 80 years [19]. These differences by age in mortality rates are primarily due to the higher prevalence of chronic diseases in older individuals, where the risk of death is greater in patients with co-existing illnesses [22]. On the other hand, individuals of younger age may be more likely to engage in risky behaviors, such as attending mass gatherings and not following safety guidelines [23], explaining the higher infection rate observed in this subgroup. However, studies that document infection and mortality rates by pre-existing conditions and risky behaviors in PR are needed.

In our study, we did not find a sex difference in the risk of infection. However, the risk of death was significantly higher in males compared to females. The more recent epidemiological data worldwide suggests that men are more affected than women by the COVID-19 virus [24-26]. However, these studies are limited by location, sample size, and other potential biases in the population examined. Different clinical studies have given conflicting reports on the male or female predominance of COVID-19 infections and deaths [24]. This discrepancy is likely due to the lack of large-scale epidemiological studies, socioeconomic disparities, or other confounders on the prevalence of pre-existing conditions in different countries.

In contrast with our findings, recent epidemiological data from 38 countries showed a male predominance in COVID-19 infections, which increased in older age demographics. Furthermore, the case fatality rate was 1.7 times higher in men than women [24]. The study's authors suggested that differences in sex hormones, sex chromosomes, genetic polymorphisms, and epigenetic modifications between males and females might impact immune responses [24]. The biological mechanism behind these differences also needs further investigation. As the COVID-19 pandemic spreads, the differences between male and female mortality and infectivity remain an area of active research. Until these mechanisms are clearly understood, it is imperative to continue prevention strategies such as physical distancing, avoiding crowds, hand washing, mask wearing, and education and promotion of the COVID-19 vaccines available to mitigate and control the pandemic.

Our results have important public health implications as they may inform about the pandemic's overall impact at the population level. Our data may also advise how to guide re-opening phases in Puerto Rico and serve as a reference for evaluating lockdown and quarantine measures in this vulnerable population. Lastly, with the current widespread vaccination efforts across the USA and in PR, our approach can serve as reference data to model the impact of vaccination [27].

The present study has several strengths and limitations. One methodological limitation is that the estimates may be burdened by the different testing procedures, inadequate testing capacity, imperfect test accuracy, varying case definitions, proportion of asymptomatic cases, and lag times in reporting laboratory test results [28-30]. In addition, because our data was from the PR Department of Health, delays in government reports, particularly in the most recent weeks, may increase the potential for under-ascertainment in the number of cases and deaths [31]. Nonetheless, the PR Department of Health data's use ensures that we have representation of all cases officially reported in PR, giving us an overview of the pandemic’s dynamics in our population. Lastly, another study strength is Lastly, the use of GAMs to estimate COVID-19 infection and mortality in PR enabled us to model complex, non-linear relationships, considering the large number of fluctuations imposed by the different government restrictions during the study period. However, caution must be taken in interpreting long-term predictions after the end of the historical period used for modeling due to their increasing uncertainty. In the case of COVID-19, we recommend making predictions for the following 2-3 weeks after the historical data becomes available. The other concern is the definition of the historical period for this pandemic due to the completeness in the number of cases and deaths, particularly for the last week of the official reports. We recommend removing the last week (or last two weeks) of the reports to avoid prediction biases in the short-term predictions.

Conclusion

In conclusion, this analysis provides evidence that increments in the number of cases in the short term are of great concern to justify more substantial preventive restrictions. Additional studies are needed to continue surveillance of COVID-19 infections and deaths in PR and explore the underlying mechanisms of age and sex disparities in COVID-19 infections and deaths in this vulnerable population.

Author Contributions

Suárez, Pérez, and Reyes conceived the study. Suárez performed all data analyses. Mattei estimated the weekly populations. Suárez and Pérez wrote a first draft of the article. Lopez-Cepero critically reviewed the manuscript. All authors reviewed the results and contributed to editing the final draft.

Data Availability

All relevant data are within the manuscript. Supporting information files with R code and data have been provided as a supplementary file.

References

Download PDF

Citation: Suarez EL, Reyes JC, Mattei H, Lopez-Cepero A and Perez CM. Modeling the Number of COVID-19 Confirmed Cases and Deaths in Puerto Rico: One-year Experience. Austin Biom and Biostat. 2021; 6(1): 1038. ISSN:2378-9840

Instruction for Authors

Submit Your Article