Boolean Logic Approach to Analyze Biomolecular Networks: A Foundation of Bio-Computing

Chaudhary N¹, Aggarwal Y², Singh N¹ and Sinha RK²*

¹Department of Electrical & Electronics Engineering, Birla Institute of Technology, India

²Department of Bio-Engineering, Birla Institute of Technology, India

*Corresponding author: Sinha RK, Department of Bio-Engineering, Birla Institute of Technology, Ranchi, 835215, India.

Received: August 25, 2014; Accepted: September 19, 2014; Published: September 23, 2014

Abstract

Various modeling approaches have been tried to understand and simulate the complex genetic and biochemical networks and to develop an efficient tool in the computational and systems biology. However, most of the time, the kinetic variables of the biochemical reactions along with identification and selection of number of molecular variables for a particular network modeling and simulation seems to be the major hurdles. Now day's researchers have started preferring the qualitative approach of modeling on the complex quantitative approaches. Being a subarea of unconventional computing, researchers proposed the idea that biological information can mimic Boolean logic operations using binary definitions, i.e. by 1/0 or YES/NO logics. Here, a brief review has been presented on Boolean modeling approach that is gaining its place very rapidly in the area of qualitative analysis of genetic and biochemical networks, which may also take a lead in development of the concept of bio-computing.

Keywords: Biochemical networks; Boolean approach; Genetic networks; Qualitative modeling

Abbreviations

DNA: Deoxyribonucleic acid; GOx: Glucose Oxidase; GDH: Glucose Dehydrogenase; AlcDH: Alcohol Dehydrogenase; MP-11: Microperoxidase-11; HGF: Hepatocyte Growth Factor; HO-1: Heme Oxygenase-1

Introduction

Living thing is a complex web of interactions between numerous genes and thousands or millions of chemical compounds. A fundamental task of biology is to explain the origin and nature of metabolic stability in such systems in terms of the mechanisms, which control biosynthesis [1]. The analogy of genetic repression and de-repression with digital computers has suggested by many researchers that the genome embodies complex switching circuits, which constitute a program for metabolic stability and cell differentiation, rather than providing a coded description of these phenomena [1,2].

Computational models are useful for providing a framework for integrating data and gaining insights into the static and dynamic behavior of complex biological systems such as networks of interacting biomolecules and genes. Biological networks are known to consist of various regulatory modules, including feedback, feed-forward regulation and cell to cell communication. With these basic regulatory modules and motifs, researchers are now constructing artificial networks that mimic nature to gain fundamental biological insight and understanding. All cellular processes involve many different molecules and many interlinked reactions; forming the metabolic network, same is true for regulatory relationships between genes and their products. Modeling of both molecular and genetic network will play an important role in understanding the living systems on biochemical and genomic level. The modeling of biochemical networks is helpful for providing an outline for integrating data and gaining insights into the static and dynamic behavior of complex biological systems.

Boolean logic based modeling approach is established among one of the best modeling approaches for better understanding of any biochemical pathway [3,4] and the review reveals that the research in this area is growing exponentially. This mini review tries to provide some practical insight on the Boolean modeling approaches of biochemical networks, and explains how this approach can be suggested as the foundation of bio-computing.

Boolean Logic Concepts in Biological Modeling

Researchers have been experimenting form many years with the idea that biology can be connected to perform computations. Biological systems can amplify and sample a large collection of molecules simultaneously. Molecular and biomolecular logic gates and their networks processing chemical input signals similarly to computers received high attention and were rapidly developed in the last decade. Being a subarea of unconventional computing, researchers proposed the idea that biological information can mimic Boolean logic operations using binary definitions (1/0; YES/NO). Construction of electrical circuits benefits from a large collection of well-characterized parts and modules, including resistors, capacitors, and inductors, which can be connected to generate a complex circuit with a useful function. Using this approach, biochemical reactions could be reformulated as information processing steps with built-in logic operations. Then, the biochemical processes could be programmed similar to computer programming yielding networks performing several logic operations.

The similarities in the processing of information by biological systems and human designed devices are broadly recognized by many researchers [5,6]. Computer technology relies on logic functions and arithmetic operations, whereby the insertion of signals into electronic circuits allows the differentiation and processing of the output signals same as in chemical or biochemical computing systems. Different stimuli trigger molecular architectures or biochemical ensembles, and the resulting chemical reactivity provides computing and processing functions [7].

Cell is a complicated device that performs three elaborate functions: sensing inputs, processing the input information for decision-making, and executing the outputs. To this end, cells have built-in sensors that can receive the input signals generated by various external and internal environmental factors [8]. Therefore, biomolecules such as Deoxyribonucleic acid (DNA) or proteins were recommended as active components that function as logic gates. Keeping this in mind, various genetic regulatory network modeling approaches in terms of Boolean logic have been proposed by number of researchers for capturing the holistic behavior of the relevant genes and biomolecule. In the Boolean idealization of the network, consists of a number of "genes" or "biomolecules", which can either be active "ON" i.e. gene/biomolecule is expressed or inactive "OFF" i.e. gene/ biomolecule is not expressed. Because this physiological cellular behavior is similar to information processing in a computing device, in the field of synthetic biology, engineering principles have been applied to study fundamental biological components [9].

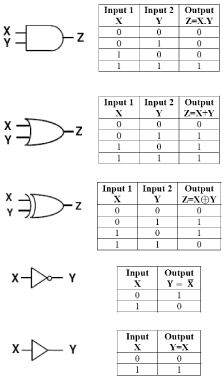
In any computing device, the input information is mathematically processed into a digital signal. Digital signals are represented in terms of binary code. The binary digits indicate the two states of the logic circuit. Digital circuits make extensive use of logic elements that are interconnected to create logic gates, capable of executing Boolean logic functions including NOT, OR, AND, and all their possible combinations. In these gates, the sensors read out inputs, and then a computational core assigns them a binary value depending on the threshold set in place. If the combination of these values meets the system requirements the output is executed. Each gate can be defined by conventional symbols or a truth table [10]. The operation of some important fundamental logic gates with their truth tables are illustrated in Figure 1.

Figure 1: Operational illustration of some important logic gates.



Figure 1:  Operational illustration of some important logic gates.

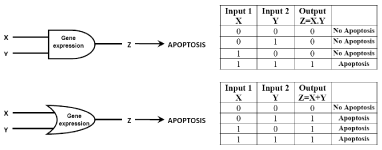
When these concepts are applied to a living cell, the values of the thresholds of input and output must be defined in a precise manner [11]. For example, if two different biomolecules, X and Y, can induce apoptosis via the production of biomolecule Z, it may be possible to create artificial logic gates that can regulate the induction of apoptosis [10]. Therefore, Boolean networks yield crude models with lower data requirements, which yield dynamic pathway information. One new sight towards this is using enzymatic reactions to create logic gates. The example of the logic gates as the processing unit for gene expression that provides the information for apoptosis by expressing the output as logic 1 has been presented in Figure 2.

Figure 2: Figure illustrates the binary model of gene expression for apoptosis with the help of 'AND' and 'OR' logic gates [10].



Figure 2:  Figure illustrates the binary model of gene expression for apoptosis with the help of 'AND' and 'OR' logic gates [10].

Boolean Network Modeling in Life Science

Boolean or logical modeling has now become a promising approach to capture the qualitative behavior of complex biological networks. In past, methods for efficiently using experimental data to construct models of large genetic networks with the Boolean method have studied and developed [3,4]. Hybrid modeling approaches, those consider analog electronic component along with digital gates have also been applied now days in which biochemical processes characterized by sharp thresholds, such as the activation of genes over a narrow concentration range of an effector molecule, are represented as Boolean switches. However, activation functions not characterized by sharp thresholds are modeled as continuous input-output relations. Either continuous time courses, or switch like functions, can be assumed for hormonal or other inputs. In this approach, macromolecular concentrations are numerically integrated as ordinary differential equations. Time delays can also be incorporated [12]. For example, the hybrid approach is used to model the E. Coli- λ phage lysis-lysogeny genetic switch [13] and for regulation of the developmental gene endo16 in sea urchin embryo [14].

Many other researchers are also working in this area. For example function of enzyme networks as mimics of Boolean logic gates was also discussed [15]. Biochemical systems demonstrating Boolean logic operations AND, OR, XOR and NOT were developed using soluble compounds representing the chemical "devices" and enzymes Glucose Oxidase (GOx), Glucose Dehydrogenase (GDH), Alcohol Dehydrogenase (AlcDH) and Microperoxidase-11 (MP-11) operating as the input signals that activate the logic gates [16]. The logic gates NAND / NOR were mimicked by enzyme biocatalyzed reactions activated by sucrose, maltose and phosphate [17]. The Boolean network-based computer model provides useful insight into main functioning logic of the Bcl-2 switch, consistent with experimental findings [18]. This modeling approach is applied for the central intrinsic and extrinsic apoptosis pathways [19] and to understand the design principles of the molecular interaction network associated with the irreversibility of cell apoptosis and the stability of cell surviving [20]. Boolean models are also implicated in fault diagnosis in oxidative stress response [21] and cancer signaling pathways [22]. It is also been used to simulate a molecular pathway between two neurotransmitter receptor, dopamine and glutamate receptor systems in order to understand the consequence of using logic gate rules between nodes, which have two possible states active and inactive [23]. Boolean logic is applied to capture the qualitative behavior as well as short- and long-term dynamics of the complex signaling network involved in (Hepatocyte Growth Factor- HGF) HGF-induced keratinocyte migration [24]. To predict the effect of heat stress on the functional genomics of Heme Oxygenase-1 (HO-1) system in vasodilation Boolean network model is applied [25]. Thus, review of literature reveals significant applications of Boolean logic in biochemical network modeling and analysis.

Conclusion

Modeling of molecular and genetic network plays very important role in understanding the living systems on biochemical and genomic level. Computational and Mathematical models are useful for providing a framework for integrating data and gaining insights into the static and dynamic behavior of complex biological systems such as networks of interacting biomolecules and genes. However, the scattered and uncertain information about the concentration of biomolecules, rate constant and time is the major barrier in modeling approaches in molecular biology. The discrete modeling is a very new approach that is gaining its space rapidly in the field of molecular and genetic network modeling. This is a qualitative approach based on the assumptions of activation of molecular nodes at a particular time point. The most ultimate simplification is the representation of activation of nodes, which is termed as binary or Boolean approach of representation of molecular activation. This is the simplest discrete model and computationally very efficient [26]. However, reasonable objections in this modeling approach are also recorded as this does not capture the richness of the dynamics of real biological system. Moreover, these objections related to the study of molecular dynamics by using Boolean approach may be addressed by adding more dynamical complexities with the help of Bayesian and Deterministic finite Automata theories.

References

Download PDF

Citation: Chaudhary N, Aggarwal Y, Singh N and Sinha RK. Boolean Logic Approach to Analyze Biomolecular Networks: A Foundation of Bio-Computing. Austin J Biotechnol Bioeng. 2014;1(4): 3. ISSN: 2378-3036

Instruction for Authors

Submit Your Article