
Review Article
Austin J Biotechnol Bioeng. 2015;2(2): 1041.
Bone Remodeling and Biomechanical Processes- A Multiphysics Approach
Farid Amirouche¹* and Aimee Bobko²
1Department of Mechanical Engineering, University of Illinois, USA
2College of Medicine, University of Illinois, USA
*Corresponding author: Farid Amirouche, Department of Mechanical Engineering, University of Illinois at Chicago, Chicago, IL, USA.
Received: March 04, 2015; Accepted: May 12, 2015; Published: May 14, 2015
Abstract
Bone remodeling is bone’s mechanism to optimize its structure in response to the body’s external and internal stimuli. From the mineralized matrix of whole bone to the lacuna canalicular network of osteocytes, mechanical and biological signaling induce changes in properties like bone density. Previous studies have made strides in simulating aspects of these processes with mathematical models. The focus is to now create a more encompassing assessment by incorporating the interdependence between bone’s macrostructure and microstructure. This work is emphasizing a multiphysics and multiscale approach in creating a model to predict the age-related changes in bone remodeling.
Introduction
From a macroscopic perspective, bone is a biological entity which is designed to obtain optimal mechanical properties to enhance the structure’s ability to support and locomote the body. Bone remodeling, in addition to providing everyday maintenance to the structure, is the phenomenon responsible for the bone’s adaptation to stimuli. In order to achieve these modifications, there is a highly active and organized system present at the cellular, microscopic level. Bone remodeling is a location specific cyclical process generally described as a resorption phase completed by cells called osteoclasts, followed by a formation phase consisting of laying down new bone matrix performed by cells called osteoblasts. Locations are designated as a site in need of bone remodeling by cells called osteocytes which become activated under increased mechanical stress. This stress can appear randomly due to the formation of microcracks or can be in direct response to a change in external mechanical loads [1]. Without the optimizing ability of the bone remodeling process, bone would be at greater risk for points of structural weakness and the potential to fracture. This is a phenomenon that due to its overlapping processes is still not well understood and has been the subject of multilevel of research.
Bone Remodeling Review
After bone is originally formed or “modeled,” the process of bone remodeling begins to take place in order to ensure the upkeep of the bone’s structural integrity. A general description of bone remodeling is the resorption of old bone, followed by the formation of new bone at designated locations, resulting in ‘targeted remodeling’ [2]. More in detail, Figure 1 shows a cyclical representation of bone remodeling divided into 5 stages: activation, resorption, reversal, formation, and quiescence [3]. Reversal is referring to the time, typically 1-2 weeks, between the resorption and formation processes at one location [4]. This cycle emphasizes the sequence of events that occur to maintain the stable architecture of bone.
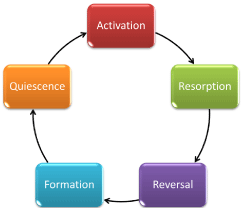
Figure 1: Bone remodeling process depicted as a five stage cycle [3].
Bone multicellular units
Locations undergoing bone remodeling, also known as bone remodeling units or Bone Multicellular Units (BMUs), are numerous within one piece of bone [5]. At any time, it has been estimated that the entire body has 105 to 106 BMUs present [4]. The BMU travels approximately 20-40 μm/day and has an average lifespan of 6-12 months [6,7,8]. Osteoclasts lead the cavity at the front, resorbing bone in order to keep progressing forward [9]. In order to do so, these cells create what are known as resorption cavities. As osteoclasts keep enlarging the BMU, a growing capillary follows to not only ensure nutrients are delivered to the surrounding cells but also to provide a constant influx of osteoblast and osteoclast precursor cells from the bone marrow [9,10]. The migration of angiogenesis is a key component of bone homeostasis [11,12,13]. Under direction from a variety of signaling mechanisms, the precursor cells will undergo a specific sequence of events in order to differentiate into mature osteoblasts and osteoclasts [14]. Through a signaling mechanism, these cells position themselves into a gradient with osteoclasts proceeding to the front and osteoblasts settling to the back [9]. The osteoblasts will secrete osteoid to reform whatever bone has been resorbed. Additionally, the osteoblasts will begin the differentiation process into osteocytes. While within the unmineralized osteoid, the cells may be referred to as pre-osteocytes [15]. Once the cells are completely surrounded by bone matrix and are no longer motile, they can then be referred to as osteocytes [16-19]. The differentiation process from osteoblast to osteocyte takes approximately 3 days [20]. The osteocytes are cells with slender extensions known as the osteocytic processes. Some of these processes are in contact with the processes of another osteocyte or an osteoblast. These connections take place through the existence of gap junctions. A gap junction is a cell structure made of proteins which allows the exchange of signals through the transport of ions and second messengers between adjacent cells as well as the delivery of small metabolites [21]. This creates a full-length communicating cell network within a bone.
Figure 2 provides a systemic diagram of the processes of bone remodeling phenomenon. There are inputs and outputs of the system including mechanical load, nutrients, hormones, precursor cell supply, and waste removal. These items can help to stimulate or inhibit the remodeling process. The internal components carrying out this process include the various cell types and the secreted product of osteoblasts, osteoid, which will eventually mineralize. All of these activities are highly balanced in relation to one another. If a mechanical or biological element is changed, the entire system depicted in Figure 2 must respond appropriately to ensure that the overall appearance of homeostasis is maintained. Specifically, if the balance of the system is disturbed, pathological conditions such as osteoporosis, Paget’s disease, and cancer can result [22].
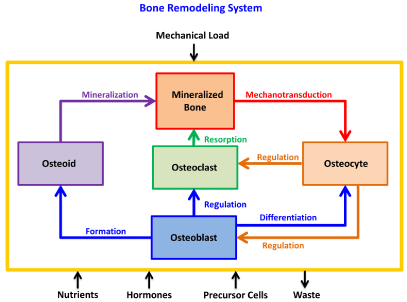
Figure 2: Bone remodeling system with labeled components and processes
that are continuously adapting to changing internal and external stimuli.
Interscale synergies
An increased mechanical load is seen as a stimulant to the bone remodeling process as it initiates the need for greater strength at the points of highest stress. In fact, it has been found that both the osteons of cortical bone and the trabeculae of cancellous bone are aligned in the same direction as the largest mechanical loads being applied to a bone [23,24]. As a result, the bone remodeling process must take action to lay down new bone in these areas. When a load is being placed upon the macroscale mineralized bone matrix, it is also resonating into strains at the nanoscale of the lacuna canalicular network of osteocytes. Cells function to maintain or increase the strength and stiffness properties back at the macroscale level. These top-to-bottom and bottom-to-top interactions otherwise known as interscale synergies, as depicted in Figure 3, have proven to be the difficulty of creating a comprehensive mathematical model of the bone remodeling phenomenon.
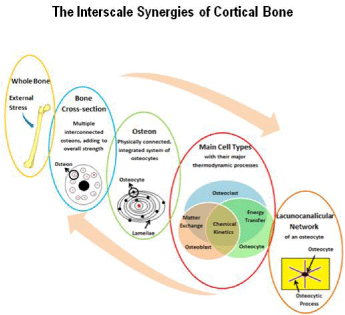
Figure 3: The interscale synergies occurring within a cortical bone’s structure.
The thermodynamic processes occurring at each scale are interconnected to
deliver the resulting whole bone properties.
More specifically at the microscale level, when an external mechanical load is applied to a piece of bone, stress throughout the whole tissue increases proportionally, creating pressure gradients within the interstitial fluid of the nanometer scale canaliculi which surround the processes of osteocytes [25]. As a result of these pressure gradients, interstitial fluid flow occurs, creating a shear stress on the osteocytic processes. This shear stress creates a deformation in the osteocytic process membrane [26,27]. It has been shown that the necessary threshold for deformation to elicit a response within the osteocyte cell body is 4.3± 0.8μm and in the osteocytic cell process is 2.0±0.5μm [26]. The difference in these values indicate that it takes a smaller deformation in the osteocytic cell process to elicit a response, thus the osteocytic cell process is more mechanosensitive than the osteocyte cell body [26]. In addition to the mechanical stimulus, the initiated interstitial fluid flow will carry nutrients and hormones which can act on the osteocytes and their signaling response [25]. It is hypothesized that the osteocyte takes in all of the various stimuli, combines their inputs, and produces an appropriate signal in response [28-32]. This signal is estimated to have an effect within a 100μm diameter [33]. The major signaling metabolic factors secreted by the osteocyte include those such as Nitric Oxide (NO) and prostaglandin E2 (PGE2) [34,35]. It is important to note that NO has an inhibitory effect on osteoclast cells, while PGE2 has a stimulatory effect on osteoblasts [4,36]. Hence, when a mechanical load is applied to bone, the cellular reaction is to enhance bone formation and limit bone resorption. However, in the case of disuse (unloading) where there is little interstitial flow to deliver NO from osteocytes to osteoclasts or in microdamage where canaliculi are damaged along with associated osteocytic cell processes, the inhibitory effect of osteocytes on osteoclasts is diminished [1,33,37,38]. Additionally, when osteocytes undergo apoptosis of cell death, which is stimulated by the lack of mechanical load such as with immobilization or weightlessness, there is less inhibitory signaling directed to surrounding osteoclasts, resulting in a weakened structure [39-44]. NO has a half-life of a few minutes which emphasizes that its paracrine actions are only effective in local regions under the current mechanical force or lack thereof [45]. Of note, it has been shown that depriving interstitial fluid of nutrients decreases the osteocyte’s responsiveness to secrete NO, even in the presence of a constant shear stress [46]. This demonstrates the importance of the biological cell requirements to a cell’s function and the need to account for this as a factor responsible for initiation and inhibition of bone remodeling [47].
The mechanosensitive osteocyte
Despite the limitation of knowing whether the signal for bone remodeling is more mechanically or biologically based, the presence or absence of a signal from an osteocyte is of great importance. In terms of bone maintenance, as stated previously, if micro damage has occurred, preventing an osteocyte’s signal from reaching osteoclasts, resorption of the surrounding damaged mineralized matrix will begin to occur [48]. The function of osteoclasts contributes to the stimulation of the osteocyte signal by first migrating to the site of localization with an average rate of 105±10μm/hour, then resorbing bone at an average rate of 165μm3/hour (as demonstrated in vitro) for approximately 2 weeks [34,49,50]. During this time, the osteoclasts create what is known a resorption cavity [1,33]. This newly developed architectural structure changes the stress distribution at this particular site and is also recognized as a mechanical stimulus by the osteocytes [1,33]. As a result of the stresses and mechanical load changes inflicted by the newly formed resorption cavity, the mechanosensitive osteocyte will secrete appropriate signals to recruit osteoblasts to the site so that new bone may be laid down within the newly formed cavity [1,33]. Osteoblasts will only be recruited if the osteocyte’s recruitment signals are above a threshold [1]. These cells will then secrete osteoid, which eventually mineralizes to bone [34]. The formation process can take place over a 3-6 month time period [34].
Intercellular regulation
Additional components of bone remodeling modulation include intercellular regulation directly between osteoblasts and osteoclasts. Cells secreting osteoid, known specifically as Active Osteoblasts (AOBs), produce an essential regulatory factor, Receptor Activator of Nuclear Factor Kappa-B Ligand (RANKL). RANKL is the factor needed to activate the RANK receptor present on the osteoclast cells. The RANK/RANKL interaction will enhance osteoclast formation and activity, to drive the cycle of resorption/formation of bone remodeling [51-53]. Resting Osteoblasts (ROBs) secrete Osteoprotegerin (OPG) which is an antagonist to the RANK/RANKL interaction by binding to RANKL to prevent its interaction with RANK and thus protect the bone from over resorption [52]. In addition to this intercellular regulation, hormones provide an additional layer of checks and balances to the bone remodeling process in response to the needs of the whole body. We will discuss two of the more prominent and studied hormones, estrogen and Parathyroid Hormone (PTH). In addition to these two, there are many other hormones as well as growth factors that have been identified as having a role in the bone remodeling process such as growth hormone, glucocorticoids, and thyroid hormones [54]. Based on the percentage of the receptors for these hormones and factors which are occupied, the cells will elicit an appropriately graded response [55]. Estrogen has been found to stimulate osteoclast apoptosis through the action of TGF-ß [55]. Thus, the overall effect is to decrease bone resorption. Hence, in a disease such as osteoporosis, which is noted to have a high incidence in post-menopausal females, it correlates that an estrogen deficiency would result in a greater amount of bone resorption [56]. Another influential hormone is PTH which acts as an informant to osteocytes and osteoblasts regarding the state of calcium concentration levels in the body’s serum [55,57]. As a result of decreased calcium serum concentration, the parathyroid glands will up regulate the secretion of PTH. PTH will then act on its receptors among the bone cells to stimulate bone resorption in order to release calcium from mineralized bone and allow its entrance into the body’s serum [58,59]. The major mechanism of action for PTH is to bind to receptors on both active and resting osteoblasts in order to increase the production of RANKL and slow the production of OPG [55]. As a result, the number of active osteoclasts will increase, resulting in greater resorption. The dynamics of biological bone remodeling activity are under many levels of regulation from systemic control, such as hormones, as well as local control, such as RANKL and OPG. The influence of both biological and mechanical forces produces changes in bone as a summation of both types of stimuli.
Mathematical Modeling of Bone Remodeling Phenomena
A typical bone has demonstrates high strength and fracture toughness [60]. Macroscopic mechanical properties such as these are defined by bone mass, architecture, and cellular activities [61]. Thus, as previously discussed, mechanical and biological processes which are taking place throughout the hierarchy of bone structure at both the macroscale and microscale during the bone remodeling process all have effects on the overall architecture [62,63]. This reinforces the fact that bone is considered an anisotropic entity in which its apparent density and stiffness vary from point to point throughout the structure [64]. In addition to spatial dependency, Doblare, et al. make the distinction that these properties also vary with time [64]. With aging, the mechanical properties of bone change. Less mobilization leads to less external loads on whole bone, decreased hormones such as estrogen in women lower the stimulus for bone formation, and there may be an age-dependent decrease in osteocyte cells [65-68]. To study these spatiotemporal properties, mathematical models of the bone remodeling phenomena have provided great insight [6,69]. Traditionally, the results of these mathematical models have then been compared to data obtained from in vivo studies of bone properties [70]. However, thus far, the current models still possess many limitations which inhibit the models from truly replicating the integrative events taking place in living bone. In order to achieve a more realistic representation, a model must account for both the mechanical and biological processes taking place as well as the interscale synergies discussed prior. The following is a review of the current methods being utilized to construct mathematical models of the bone remodeling process. Some of the key bone properties able to be modeled as of yet include external mechanical load, bone density, stress, strain, entropy, chemical kinetics, and interstitial shear stress. It is important to note that trabecular bone undergoes a higher rate of bone remodeling than cortical bone; thus, making cortical bone more stable and thus responsible for the maintenance of bone properties over time [71]. The objective of this paper is to provide a sampling of the key progress made in the field thus far and commentary on how interscale synergies may be bridged so that the possibility and need for a mathematical model which encompasses the multiphysics, multiscale complexities is depicted.
External mechanical loads
We first look at a major stimulus of bone remodeling, the presence of mechanical loads on the external surface of the mineralized matrix of bone. An example of such loads is the forces applied during movements such as gait. Figure 4 shows an example of some of the mechanical forces applied to a femur by surrounding muscles [72]. In order to accurately model the mechanical loads being transferred from the muscles, the force, direction, angle, time of duration, and distance of effectiveness should be characterized and accounted for. As these mechanical loads are present at the same time, their individual effects must then be summated. Ideally, to fully characterize the external mechanical loads being applied to a femur, the properties of all muscles involved could be included.
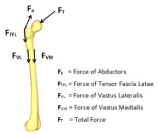
Figure 4: A femur labeled with the forces of some of the muscle involved
with gait [72].
Probability of bone surface location being subject to remodeling
Huiskes, et al. introduces a concept to look at why and where bone remodeling takes place at specific sites. The basis of the idea states that bone remodeling is either occurring for one of two reasons. One is that it is randomly acting to repair microcracks as a part of regular bone maintenance. The other is that the process is being activated at specific locations which are under an increased amount of mechanical load. The probability of a bone surface location being subject to remodeling, is defined as
hypothesis I: p(x, t) = 10% (spatially random) (1) [1]
hypothesis II: p(x, t) = c[a- P(x, t)], if P < a (strain dependent)
This theory allows for the incorporation of both the major callsto- action of bone remodeling including bone maintenance and bone adaption. However, as previously stated, the incorporation of biological stimuli is again not being considered in this concept.
Bone density
Being able to predict changes in bone density may be able to provide insight into how to treat clinical ailments such as osteoporosis. A variety of factors previously discussed influence the formation or resorption of bone which have a direct impact on bone density. The change in total bone mass has been defined as the difference of the amount of bone mass accumulated and the amount of bone mass degraded by the formation and resorption processes, seen as
Bone density is a unique property for mathematical models of bone remodeling to consider as it can be defined at the macroscale for total bone density (g/cm²) as well as for a defined smaller volume or local volume of bone at the microscale (g/μm²). A visual representation of a local volume of bone is shown in Figure 5 which is represented by a cube which can change density over time, represented by based on the effects of stimuli such as the load, FL, being applied as a result from the total external force, FT (as seen in Figure 4), acting upon the femur.
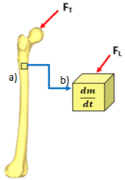
Figure 5: a) A femur under the influence of total force, FT (as seen in Figure
4). b) A cube representing a small, local, volume of bone from the femur
which is under the influence of force of mechanical load, FL, derived from FT.
The cube changes density over time, dm/dt as a result of the formation and
resorption processes of bone remodeling based on the effects of stimuli such
as the load FL.
In current models such as Ruimerman, et al. [33], the total change in bone mass has been defined mathematically in a biological manner by incorporating the actions of two of the major bone cell types, osteoblasts and osteoclasts, defined as
This equation follows the work by Huiskes, et al. [1] who defined the relationship for the local change in bone mass, like for the cube seen in Figure 5, as
Huiskes, et al. also incorporates the use of cellular bone remodeling signaling by utilizing a decay function as recruitment stimulus for osteoblasts to become active and participate in bone formation, seen as
The decaying effect indicates that the signal has a specific effective distance range, exhibited by osteocytes in vivo, as mentioned previously; thus, the role of osteocytes and their signaling mechanisms in bone remodeling regulation is recognized.
Both Huiskes, et al. and Ruimerman, et al. make the assumption that osteoblast recruitment, ρ(x ,t), can be equated with bone formation and if the amount of bone mineral resorbed by osteoclasts, roc, is subtracted, the change in local bone mass over time can be measured [1,33]. It is not known if this assumption regarding bone formation is indeed true as it is unclear if every recruited osteoblast is activated to secrete osteoid. In addition, neither model considers the effects of biological stimuli such as the effects of hormones. Furthermore, in both models, the mechanosensitivity of the osteocyte, μ, is being considered as one value rather than accounting for the differences in mechanosensitivities exhibited among the osteocyte cell body and the osteocyte cell processes. In addition, there is no representation of the shear stress taking place at the lacuna canalicular network which is initiating the mechanical stimulus for osteocyte cell signaling to take place. By accounting for these elements, a more comprehensive multiphysics, multiscale model may be able to be derived.
A model which attempts to bridge from the microscale properties defined by Huiskes, et al. to the macroscale by relating their densities to one another is presented by Coelho, et al. [73]. An insightful representation of what is called the bone remodeling law, where it is assumed that structural stiffness will be maximized and metabolic cost, k, will be minimized is applied in order to achieve such a relationship [73]. In this model, it is recognized that the time scale of the bone remodeling process is much larger than the scale for an applied force to whole bone, accounting for the temporal dependency defined earlier. As a result, the forces are evaluated as a summation of P loads over time [73]. This design allows for the model to account for both processes, applied force and bone remodeling, in a more accurate manner. In order to carry out this two-scale approach, Coelho, et al. defined variables to macroscale properties of whole bone as well as microscale properties among the trabeculae of cancellous bone [73]. The macro-density, ρ, can be related to the micro-density, μ, as seen in the following
The bone remodeling law for this model, which accounts for the different time scales of mechanical loading and bone remodeling, is defined as
This model provides a foundation for interconnecting the macroand micro- scales. However, it would still be of great interest to define total density in terms of both space and time, ρ(x ,t). It may be possible to add to this model the changes of density as a function of time through probability calculations from data collected by current technology using DEXA scans. In addition, the limitations of the model provided by Coelho, et al. lack the inclusion of bone cell populations and activities including biological stimuli and signaling as well as the incorporation of the lacuna canalicular system.
Mechanosensitivity and intercellular signaling
Huiskes, et al. only goes so far as to define the osteocyte’s mechanosensitivity as a general variable, μ. Adachi, et al. provide a model which specify an actual relationship for mechanosensitivity which incorporates the physical parameters of canaliculi as well as osteocyte processes, seen as
For simplicity, the cell processes are assumed to extend isotropically in the radial direction, thus the canalicular volume fraction would not depend on orientation n. Adachi, et al. go on to mathematically define the intercellular signaling communication between osteocytes and surface cells (such as osteoblasts and osteoclasts), written as
It is important to note that in addition to the other mentioned, the Adachi, et al. model does not account for the incorporation of biological stimuli such as hormones or the biological regulation through factors such as the RANK-RANKL system.
A model which does emphasize the additional role of biological element contribution (for example, from calcium or PTH) in the outgoing signal from an osteocyte, along with the thoroughly discussed mechanical stimulus is provided by Rieger, et al [57]. This model accounts for both the mechanical and biological components in the signal traveling to an osteocyte by adding a weight factor for each part, shown as
Ψ = WMecha < fMecha > +WBio < fBio > (10) [57]
This method offers a way to quantitatively measure the mechanobiological stimulus reaching the osteocytes. However, while this is a valid conceptual conclusion, a limitation of this model is that it is still not known what the appropriate physiologic weight factors are.
Interstitial shear stress
Interstitial shear stress along the osteocyte process is the cause of osteocyte cell activation. This stress is modified by properties of the canaliculi structure such as the size and permeability of these channels. As discussed previously, the osteocyte cell process has been proven to more sensitive to shear stress deformation than the cell body. Figure 6 shows the effect of an external mechanical force, FT (from Figure 4), which is transduced into an internal mechanical load force, FL (from Figure 5), in creating an interstitial shear force, τ, within the canaliculi of one of the osteocyte processes shown. The osteocyte will then take in these mechanical stimuli in addition to biological stimuli, and after a summation, the cell will produce an appropriate signal which will be transmitted via gap junctions to the laboring cells of bone remodeling, the osteoblasts and osteoclasts.
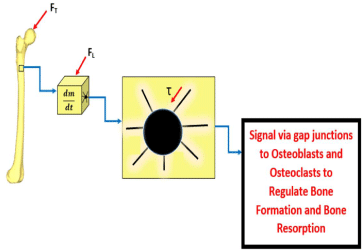
Figure 6: This is an expansion of the sequence displayed in Figure 5. This
image now shows an in-depth look of an osteocyte present within the small
volume of bone shown in b). c) depicts an osteocyte cell with several cell
processes lying in the lacunocanalicular network (surrounding white space).
It is in this lacunocanalicular network which is filled with interstitial fluid. The
interstitial fluid changes its flow rate and thus shear stress on the basis of the
mechanical forces present. Thus, in this case, the external mechanical force,
FT, seen in a) was transmitted as the internal mechanical load force, FL, to the
local volume of bone seen in b) and finally transduced as a shear stress in c).
Adachi, et al. derive the interstitial shear stress being applied to osteocyte processes through the relationship stated as
n where constants A1 and B1 are given by
Hambli and Korta also developed a model to simulate internal bone remodeling and the effects of interstitial fluid in the lacunocanalicular network. Their model is more progressive as it includes the velocity of the fluid as an additional contributing factor utilizing Bernoulli’s and Darcy’s law:
Rate of change in interstitial bone fluid calcium concentration
Pennline recognizes the importance of calcium homeostasis in the regulation of bone formation and resorption, so he provides a definition of the rate of change of calcium in interstitial bone fluid, expressed as
Developing more equations such as these for other important metabolic factors in the interstitial fluid, for instance, NO and PGE2 secreted from the osteocyte, would provide more information regarding the local environment concentration changes the osteocyte withstands and responds to.
Rate of change of cortical bone area
Pennline presents another property of bone that could be modeled and has the potential to reveal insight into the bone remodeling process [4]. Looking at a cross-section sample of cortical bone, Pennline first references Martinto define what will be considered as the intracortical bone balance, expressed as
Q = QBNF - QCNR (14) [75]
The rate of bone formation is then related as
and bone resorption is given by
Pennline then goes on to reference Martin’s definition of porosity, seen as
All of these relationships are then used to establish an equation for the rate of change of cortical bone area in a cross-section sample, expressed as
While the equation above can provide a suitable estimate of the change in bone area over time, its major limitation is that bone is being defined in a simplified form as a perfect cylinder. However, this is not the case. One way to better account for the real structure of bone may be to use Finite Element Analysis (FEA) for instance in order to maintain the actual shape and 3D elements of bone. Also, in addition to accounting for the change in concentration of osteoblasts and osteoclast cell types, osteocyte concentration could also be incorporated. With these changes in cell type densities, it would be important to consider the rate of cell apoptosis as in the model developed by Buenzli [76].
Stress and strain
From the induction of mechanical loads on the bone, stress and strains arise within the mineralized matrix and serve as stimuli to the bone remodeling process [77]. For this last section, we will present a look into how these bone properties can be approached from a mechanobiological perspective within the multiscale system. For example, consider a small area, ΔA, around P of the cutting plane of a deformed configuration shown in Figure 7. Let the internal resultant forces be represented by ΔF acting on ΔA.
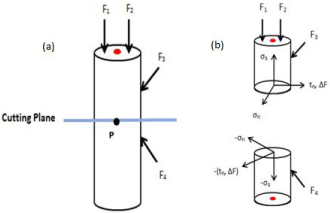
Figure 7: a) Simplified image representing the diaphysis of a bone. Different
forces being placed upon the bone are represented by F1, F2, F3, and F4.
The blue line represents the cutting plane with a center Point P. b) Same
representation now cut along the plane with the stress tensor, tn, normal
stress, σn, and the shear stress, σs.
The stress is a measure of the intensity of internal forces generated within the body of the cross sectional area and will vary from point to point. We define the stress tensor at Point P as:
With the normal stress defined as
and the shear stress defined as
In addition, due to the law of action and reaction, on the opposite side of the cut plane, we will have -tn, -sn, and -ss. This can be further generalized to 3 planes with
tn = txnx + tyny + tznz(22)
and can be simplified with the use of Cauchy’s stress tensor relation
Now, if we proceed to a smaller scale and examine a point on the trabecular bone at an arbitrary cross sectional area and assume that the accumulation vector of the deformed configuration is given by
and let the external force per unit mass of the bone be given by
Then, by using the balance of linear momentum, we can now write the following to define bone density in terms of stress:
which can be simplified to
Next, we consider the strain which can be defined by
Or
Note, that in most mechanical systems ∇ºis of the order of 10-6, but in this case, ∇º is of the order 10-9 or less. There are 3 sets of equations that govern the displacements, strains, and stresses in an element. Assuming small deformations and linear elastic material, we have in an index notation
With
and Poisson’s ratio
Linear Rotational Formulation: If we assume that the constitutive equation above in terms of stress-strain relation are applied to a deformable body, assuming an isotropic material to simplify the calculations, we obtain
Viscoelastic Behavior Formulation: There are several scenarios that explain the bone formation, resorption, and its dynamic response to load. With time, as in stress relaxation, the energy to increase bone formation also decreases. So at the initial state of bone formation, a highforceis imposed and maintained until the bone stress begins to decrease. Furthermore, if the stress maintained is constant and the bone strain increases, a phenomenon close to creep, then one has to assume that the bone formation can continue for a period of time, under the same stress or loading conditions. The rate of bone formation is directly associated with the velocity as in the case of a Maxwell model,
The constitutive equations for numerical simulation for at least 2D models result in
Chemical Virtual Work Traction acting at the (stress-strain) Boundary of the cell
There are two sources of elastic response to deformation: change of internal energy and change of entropy. Assuming we have conservation of energy, we can examine how the laws of thermodynamics connect to internal energy: Ρ (energy per unit mass), S (entropy per unit mass), T (temperature), p (pressure), V (volume), ρ (density), σij (stress), ∈ij (strain), and σij ‘∈ij’ (stress-strain deviations). If we let dQ be the energy transferred to the body, then
dQ = T dS (37)
With and
If the material is perfectly elastic, then the existence of a strain-energy function can often be justified on the basis of thermodynamics. However, living tissues are not perfectly elastic, and therefore, they cannot have an energy function in terms of strain-energy function in the thermodynamics sense. If we can ensure that the rate of bounding and unbounding is such that the strain rate is small and can be ignored, as is the case for bone remodeling, than the stress-strain can be uniquely defined.
Mapping Functions and Bone Remodeling
The cells live under continuous stress which causes them to participate and engage in a metabolic internal reaction as well as protein resorption and mass change due to the energy being diminished and produced. While preserving the constitutive laws of physics, the mechanical change in terms of mass, geometry, play a role in the local and global space and time frame (aging process).
The constitutive laws are directly related through variables:
The cross-bridge concept of creating mapping functions is to help us understand the inter-relationship between the biological, mechanical functions can be defined using probabilistic finite elements, where the cross bridge is at a finite point in space and time (n,t). The Lagrangian stress can be appreciated with the instantaneous energy and mass as it relates to stiffness. The bounding and unbounding of matters and energy are probabilistically determined based on a set of variables that are determined and defined by
where f and Q are functions describing the bounding and unbounding of energy processes.
What remains to be defined is the extraction of these functions for different mechanisms including chemical reactions, transport phenomenon, energy dissipation, and the creation of matter.
Developing a Comprehensive Model
The goal of this research was to identify the applicability, needs, and limitations in building a comprehensive multiphysics, multiscale model which would ultimately be able to predict age-related changes in bone remodeling. New developments with current technology such as μ CT allow for imaging and quantitative 3D visualization of smaller scale structures of bone such as osteons and the lacuno canalicular network [78-82]. By being able to obtain more defined and realistic properties of these structures, mathematical models will greatly improve [83]. Animal and clinical studies such as Webster, et al. which was able to calculate strain energy density gradients of mice vertebrae will offer methods for obtaining these values [84]. Ideally, it is best to not only incorporate bone’s properties and interactions but also those properties and interactions of surrounding supporting structures, such as muscles and ligaments [85]. In addition to accounting for all of these essential factors, the model needs to recognize the spatialtemporal dependency of the bone remodeling process [86]. In Figure 8, we propose a demonstration of the co-dependency of the time scale of the bone remodeling process on the spatial structure of the bone matrix.
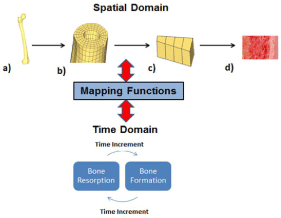
Figure 8: The dependent spatial-temporal relationship of the bone
remodeling process and the intermediate role of mathematical models
(mapping functions). a) whole bone matrix scale, b) cortical bone matrix scale
c) osteon scale d) cellular scale.
To build this model, the Orthopedic Research Laboratory at UIC is taking a patient-based, evidence-based research methodology. Our model is being based on the following four elements, specifically focused at the hip joint:
- Bone Mineral Density Scans (DEXA), Computer Tomography (CT), EMG, and gait analysis performed on young and older patients
- Cadaveric studies of pelvis-femur loading for healthy and osteoporotic bone
- 3D dynamic and probabilistic Finite Element (FE) modeling to describe the effects of altered muscle forces on dynamic changes in bone
- Development and validation of a novel multiphysics dynamic mathematical model of bone remodeling in response to internal and external stimuli
In order to create such an encompassing model as stated in point 4 above, the mechanical, biological, and biochemical interactions of bone need to be included. We propose a model such as that shown in Figure 9 which displays all three components functioning in a multiscale fashion to produce a complex, realistic model of cancellous bone within the femur. The Figure 9 shows a Finite Element Analysis (FEA) model of the femur and pelvis which we developed to assess the stress-strain relationships changing over time within the bones of the hip joint. The model was generated by utilizing the mapping functions referred to in the previous section in order to account for the cellular and whole bone responses to both internal and external forces. Our ability to use dynamic and probabilistic finite element modeling where the material properties information can be updated over time can be applied to study bone remodeling, load effects, and the changes of aging bone.
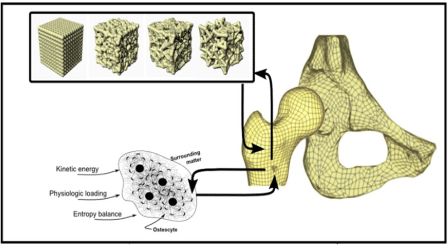
Figure 9: Finite Element Analysis model of the continuous multiscale
mechanical, biological, and biochemical interactions taking place in bone.
The osteons with embedded osteocytes depicted in the bottom left represent
the integration of all three types of interactions. The feedback from such
integration applied to a manufactured mathematical model can mold a
standard matrix into a structure correlating to cancellous bone in the femur.
The proposed model could potentially be included in the risk assessment and diagnosis of musculoskeletal diseases as well as in the planning of orthopedic procedures. This patient-specific approach could be useful, for example, in the management of osteoporosis, preparation for hip arthroplasty, and development of prosthetic materials [87]. Figure 10 emphasizes this by showing how the model could be used to study bone changes in response to an orthopedic implant. The reason why we first developed a model focusing on the hip joint was so that the model could be used to examine the bonemetal interface of an orthopedic implant such as the stem of a total hip arthroplasty. This illustrates the potential capability of being able to predict the impending bone remodeling changes and stress shielding induced by an orthopedic implant on an individual basis [88,89]. Such information could result in the reduction of the number of orthopedic implant failures and the improvement of patient outcomes with these procedures.

Figure 10: The top image illustrates the modeled bone interface with an
orthopedic implant. The three bottom bone matrices illustrate three degrees
of osteoporosis implemented with three different density values simulated
with 500, 300, and 100 randomized nodes in the reference volume.
Conclusion
Bone remodeling is a complex process due to its multiscale and multiphysics interactions. The main regulator of these processes is the osteocyte cell which is able to assimilate a multitude of incoming signals and produce the appropriate output signals to the other significant bone cells, osteoblasts and osteoclasts. In this coordinated system, each cell plays a role in building a mineralized matrix which can sustain mechanical loads and provide adequate strength. Our goal is that mathematical modeling of bone remodeling can provide insight into the conditions of this system in order to accurately predict how bone will adapt under various mechanical and biological conditions including injury, surgical procedures, and pathologies. While models thus far have provided key points of understanding, there are still many limitations which prevent a comprehensive, more lifelike model from being achieved. The model needs to not only incorporate the multiphysics and multiscale phenomena to obtain an integrative model. With the inclusion of technologies, such as DEXA, CT, EMG, and gait analysis with FEA, and incorporating more the complexities of the multiple biological and mechanical factors into mathematical models, the closer a comprehensive model becomes to being more informative and obtainable.
References
- Huiskes R, Ruimerman R, van Lenthe GH, Janssen JD . Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature. 2000; 405: 704-706.
- Martin RB. Targeted bone remodeling involves BMU steering as well as activation. Bone. 2007; 40: 1574-1580.
- Maldonado S, Frank Allgower, Rolf Findeisen. Global Sensitivity Analysis of Force Induced Bone Growth and Adaptation Using Semidefinite Programming. Proc. of the 3rd Found. Syst. Biol. Engin. (FOSBE), Denver, USA. 2009; 141–144.
- Pennline J. NASA- Simulating Bone Loss in Microgravity Using Mathematical Formulations of Bone Remodeling. NASA/TM. 2009; 215824: 1-21.
- Parfitt AM. The mechanism of coupling: a role for the vasculature. Bone. 2000; 26: 319-323.
- Ryser MD, Nigam N, Komarova SV. Mathematical modeling of spatio-temporal dynamics of a single bone multicellular unit. J Bone Miner Res. 2009; 24: 860-870.
- Buenzli PR, Jeon J, Pivonka P, Smith DW, Cummings PT. Investigation of bone resorption within a cortical basic multicellular unit using a lattice-based computational model. Bone. 2012; 50: 378-389.
- Parfitt AM. Osteonal and hemi-osteonal remodeling: the spatial and temporal framework for signal traffic in adult human bone. J Cell Biochem. 1994; 55: 273-286.
- Buenzli PR, Pivonka P, Smith DW. Spatio-temporal structure of cell distribution in cortical bone multicellular units: a mathematical model. Bone. 2011; 48: 918-926.
- Tang Y, Wu X, Lei W, Pang L, Wan C, Shi Z, et al. TGF-beta1-induced migration of bone mesenchymal stem cells couples bone resorption with formation. Nat Med. 2009; 15: 757-765.
- Kanczler JM, Oreffo RO. Osteogenesis and angiogenesis: the potential for engineering bone. Eur Cell Mater. 2008; 15: 100-114.
- Barou O, Mekraldi S, Vico L, Boivin G, Alexandre C, Lafage-Proust MH. Relationships between trabecular bone remodeling and bone vascularization: a quantitative study. Bone. 2002; 30: 604-612.
- Sacchetti B, Funari A, Michienzi S, Di Cesare S, Piersanti S, Saggio I, et al. Self-renewing osteoprogenitors in bone marrow sinusoids can organize a hematopoietic microenvironment. Cell. 2007; 131: 324-336.
- Buenzli PR, Pivonka1 P, Gardiner BS, Smith DW, Dunstan CR, Mundy GR. Theoretical analysis of the spatio-temporal structure of bone multicellular units. Proceedings of the WCCM/APCOM 2010, Sydney IOP Conf Ser Mater Sci Eng. 2010;10.
- Burger EH, Klein-Nulend J. Mechanotransduction in bone--role of the lacuno-canalicular network. FASEB J. 1999; 13: S101-S112.
- Hollister SJ, Kikuchi N. Homogenization theory and digital imaging: A basis for studying the mechanics and design principles of bone tissue. Biotechnol Bioeng. 1994; 43: 586-596.
- Dallas SL, Bonewald LF. Dynamics of the transition from osteoblast to osteocyte. Ann N Y Acad Sci. 2010; 1192: 437-443.
- Franz-Odendaal TA, Hall BK, Witten PE. Buried alive: how osteoblasts become osteocytes. Dev Dyn. 2006; 235: 176-190.
- Bell LS, Kayser M, Jones C. The mineralized osteocyte: a living fossil. Am J Phys Anthropol. 2008; 137: 449-456.
- Knothe Tate ML, Adamson JR, Tami AE, Bauer TW. The osteocyte. Int J Biochem Cell Biol. 2004; 36: 1-8.
- Meşe G, Richard G, White TW. Gap junctions: basic structure and function. J Invest Dermatol. 2007; 127: 2516-2524.
- Ayati BP, Edwards CM, Webb GF, Wikswo JP. A mathematical model of bone remodeling dynamics for normal bone cell populations and myeloma bone disease. Biol Direct. 2010; 5: 28.
- van Oers RF, Ruimerman R, Tanck E, Hilbers PA, Huiskes R. A unified theory for osteonal and hemi-osteonal remodeling. Bone. 2008; 42: 250-259.
- Hert J, Fiala P, Petrtýl M. Osteon orientation of the diaphysis of the long bones in man. Bone. 1994; 15: 269-277.
- Adachi T, Kameo Y, Hojo M. Trabecular bone remodelling simulation considering osteocytic response to fluid-induced shear stress. Philos Trans A Math Phys Eng Sci. 2010; 368: 2669-2682.
- Adachi T, Aonuma Y, Tanaka M, Hojo M, Takano-Yamamoto T, Kamioka H. Calcium response in single osteocytes to locally applied mechanical stimulus: differences in cell process and cell body. J Biomech. 2009; 42: 1989-1995.
- Klein-Nulend J, Bacabac RG, Mullender MG. Mechanobiology of bone tissue. Pathol Biol (Paris). 2005; 53: 576-580.
- Marotti G. The osteocyte as a wiring transmission system. J Musculoskelet Neuronal Interact. 2000; 1: 133-136.
- Bonewald LF. Osteocytes as dynamic multifunctional cells. Ann N Y Acad Sci. 2007; 1116: 281-290.
- Noble BS. The osteocyte lineage. Arch Biochem Biophys. 2008; 473: 106-111.
- Hambli R, Rieger R. Physiologically based mathematical model of transduction of mechanobiological signals by osteocytes. Biomech Model Mechanobiol. 2012; 11: 83-93.
- Atkins GJ, Findlay DM. Osteocyte regulation of bone mineral: a little give and take. Osteoporos Int. 2012; 23: 2067-2079.
- Ruimerman R, Hilbers P, van Rietbergen B, Huiskes R. A theoretical framework for strain-related trabecular bone maintenance and adaptation. J Biomech. 2005; 38: 931-941.
- Maldonado S, Findeisen R, Allgöwer F. Describing force-induced bone growth and adaptation by a mathematical model. J Musculoskelet Neuronal Interact. 2008; 8: 15-17.
- Noble BS, Reeve J. Osteocyte function, osteocyte death and bone fracture resistance. Mol Cell Endocrinol. 2000; 159: 7-13.
- Brandi ML, Hukkanen M, Umeda T, Moradi-Bidhendi N, Bianchi S, Gross SS, et al. Bidirectional regulation of osteoclast function by nitric oxide synthase isoforms. Proc Natl Acad Sci U S A. 1995; 92: 2954-2958.
- Muir P, Sample SJ, Barrett JG, McCarthy J, Vanderby R Jr, Markel MD, et al. Effect of fatigue loading and associated matrix microdamage on bone blood flow and interstitial fluid flow. Bone. 2007; 40: 948-956.
- Hazenberg JG, Freeley M, Foran E, Lee TC, Taylor D . Microdamage: a cell transducing mechanism based on ruptured osteocyte processes. J Biomech. 2006; 39: 2096-2103.
- Bellido T. Osteocyte Apoptosis Induces Bone Resorption and Impairs the Skeletal Response to Weightlessness. BoneKEy. 2007; 4: 252-256.
- Jilka RL, Weinstein RS, Parfitt AM, Manolagas SC. Quantifying osteoblast and osteocyte apoptosis: challenges and rewards. J Bone Miner Res. 2007; 22: 1492-1501.
- Kurata K, Fukunaga T, Matsuda J, Higaki H. Role of mechanically damaged osteocytes in the initial phase of bone remodeling. International Journal of Fatigue. 2007; 29: 1010-1018.
- Noble B. Bone microdamage and cell apoptosis. Eur Cell Mater. 2003; 6: 46-55.
- Seeman E. Osteocytes--martyrs for integrity of bone strength. Osteoporos Int. 2006; 17: 1443-1448.
- Aguirre JI, Plotkin LI, Stewart SA, Weinstein RS, Parfitt AM, Manolagas SC, et al. Osteocyte apoptosis is induced by weightlessness in mice and precedes osteoclast recruitment and bone loss. J Bone Miner Res. 2006; 21: 605-615.
- Burger EH, Klein-Nulend J, Smit TH . Strain-derived canalicular fluid flow regulates osteoclast activity in a remodelling osteon--a proposal. J Biomech. 2003; 36: 1453-1459.
- Donahue TL, Haut TR, Yellowley CE, Donahue HJ, Jacobs CR. Mechanosensitivity of bone cells to oscillating fluid flow induced shear stress may be modulated by chemotransport. J Biomech. 2003; 36: 1363-1371.
- Botchwey EA, Dupree MA, Pollack SR, Levine EM, Laurencin CT. Tissue engineered bone: measurement of nutrient transport in three-dimensional matrices. J Biomed Mater Res A. 2003; 67: 357-367.
- Hadjidakis DJ, Androulakis II . Bone remodeling. Ann N Y Acad Sci. 2006; 1092: 385-396.
- Kanehisa J, Heersche JN. Osteoclastic bone resorption: in vitro analysis of the rate of resorption and migration of individual osteoclasts. Bone. 1988; 9: 73-79.
- Ali NN, Boyde A, Jones SJ. Motility and resorption: osteoclastic activity in vitro. Anat Embryol (Berl). 1984; 170: 51-56.
- Boyle WJ, Simonet WS, Lacey DL . Osteoclast differentiation and activation. Nature. 2003; 423: 337-342.
- Teitelbaum SL. Bone resorption by osteoclasts. Science. 2000; 289: 1504-1508.
- Zumsande M, Stiefs D, Siegmund S, Gross T. General analysis of mathematical models for bone remodeling. Bone. 2011; 48: 910-917.
- Hadjidakis DJ, Androulakis II . Bone remodeling. Ann N Y Acad Sci. 2006; 1092: 385-396.
- Lemaire V, Tobin FL, Greller LD, Cho CR, Suva LJ. Modeling the interactions between osteoblast and osteoclast activities in bone remodeling. J Theor Biol. 2004; 229: 293-309.
- Kameda T, Mano H, Yuasa T, Mori Y, Miyazawa K, Shiokawa M, et al. Estrogen inhibits bone resorption by directly inducing apoptosis of the bone-resorbing osteoclasts. J Exp Med. 1997; 186: 489-495.
- Rieger R, Hambli R, Jennane R. Modeling of biological doses and mechanical effects on bone transduction. J Theor Biol. 2011; 274: 36-42.
- Raisz LG. Physiology and pathophysiology of bone remodeling. Clin Chem. 1999; 45: 1353-1358.
- Zhang Q, Miller C, Bible J, Li J, Xu X, Mehta N, et al. Additive Effects of Mechanical Marrow Ablation and PTH Treatment on de Novo Bone Formation in Mature Adult Rats. Cells. 2012; 1: 1168-1181.
- Matthew J Olsztaa, Xingguo Chenga, Sang Soo Jee, Rajendra Kumar, Yi-Yeoun Kima, Michael J Kaufman, et al. Bone Structure and Formation: A new perspective. Materials Science and Engineering R. 2007; 58: 77-116.
- Allen M, Burr D. Skeletal Microdamage: Less About Biomechanics and More About Remodeling. Clinical Reviews in Bone and Mineral Metabolism. 2008; 6: 24-30.
- Pivonka P, Pascal R Buenzli, Stefan Scheiner, Christian Hellmich, Colin R Dunstan. The influence of bone surface availability in bone remodeling-A mathematical model including coupled geometrical and biomechanical regulations of bone cells. Engineering Structures. 2013; 47: 134-147.
- Weiner S, Traub W. Bone structure: from angstroms to microns. FASEB J. 1992; 6: 879-885.
- Doblaré M, García JM. Anisotropic bone remodelling model based on a continuum damage-repair theory. J Biomech. 2002; 35: 1-17.
- Busse B, Djonic D, Milovanovic P, Hahn M, Püschel K, Ritchie RO, et al. Decrease in the osteocyte lacunar density accompanied by hypermineralized lacunar occlusion reveals failure and delay of remodeling in aged human bone. Aging Cell. 2010; 9: 1065-1075.
- Carpentier VT, Wong J, Yeap Y, Gan C, Sutton-Smith P, Badiei A, et al. Increased proportion of hypermineralized osteocyte lacunae in osteoporotic and osteoarthritic human trabecular bone: implications for bone remodeling. Bone. 2012; 50: 688-694.
- Ma YL, Dai RC, Sheng ZF, Jin Y, Zhang YH, Fang LN, et al. Quantitative associations between osteocyte density and biomechanics, microcrack and microstructure in OVX rats vertebral trabeculae. J Biomech. 2008; 41: 1324-1332.
- Vashishth D, Verborgt O, Divine G, Schaffler MB, Fyhrie DP. Decline in osteocyte lacunar density in human cortical bone is associated with accumulation of microcracks with age. Bone. 2000; 26: 375-380.
- Pivonka P, Komarova SV. Mathematical modeling in bone biology: from intracellular signaling to tissue mechanics. Bone. 2010; 47: 181-189.
- Adachi T, Tsubota K, Tomita Y, Hollister SJ. Trabecular Surface Remodeling Simulation for Cancellous Bone Using Microstructural Voxel Finite Element Models. J Biomech Eng. 2001; 123: 403-409.
- Manolagas SC, Jilka RL. Bone marrow, cytokines, and bone remodeling. Emerging insights into the pathophysiology of osteoporosis. N Engl J Med. 1995; 332: 305-311.
- Lerch M, Kurtz A, Stukenborg-Colsman C, Nolte I, Weigel N, Bouguecha A, et al. Bone Remodeling after Total Hip Arthoplasty with a Short Stemmed Metaphyseal Loading Implant: Finite Element Analysis Validated by a Prospective DEXA Investigation. J Orthop Res. 2012; 30: 1822-1829.
- Coelho PG, Fernandes PR, Rodrigues HC, Cardoso JB, Guedes JM. Numerical modeling of bone tissue adaptation--a hierarchical approach for bone apparent density and trabecular structure. J Biomech. 2009; 42: 830-837.
- Hambli R, A Kourta. A theory for internal bone remodeling based on interstitial fluid velocity stimulus function. Applied Mathematical Modellins. 2014.
- Martin RB. The usefulness of mathematical models for bone remodeling. Yearbook of Physical Anthropology. 1985; 28: 227-236.
- Buenzli PR. Osteocytes as a record of bone formation dynamics: a mathematical model of osteocyte generation in bone matrix. J Theor Biol. 2015; 364: 418-427.
- Li J, Li H, Shi L, Fok AS, Ucer C, Devlin H, et al. A mathematical model for simulating the bone remodeling process under mechanical stimulus. Dent Mater. 2007; 23: 1073-1078.
- Cooper DM, Erickson B, Peele AG, Hannah K, Thomas CD, Clement JG. Visualization of 3D osteon morphology by synchrotron radiation micro-CT. J Anat. 2011; 219: 481-489.
- Schneider P, Meier M, Wepf R, Müller R. Towards quantitative 3D imaging of the osteocyte lacuno-canalicular network. Bone. 2010; 47: 848-858.
- Cooper DM, Thomas CD, Clement JG, Hallgrímsson B. Three-Dimensional Microcomputed Tomography Imaging of Basic Multicellular Unit-Related Resorption Spaces in Human Cortical Bone. Anat Rec A Discov Mol Cell Evol Biol. 2006; 288: 806-816.
- Cooper DM, Turinsky AL, Sensen CW, Hallgrímsson B. Quantitative 3D analysis of the canal network in cortical bone by micro-computed tomography. Anat Rec B New Anat. 2003; 274: 169-179.
- Arhatari BD, Cooper DM, Thomas CD, Clement JG, Peele AG. Imaging the 3D structure of secondary osteons in human cortical bone using phase-retrieval tomography. Phys Med Biol. 2011; 56: 5265-5274.
- Rho JY, Kuhn-Spearing L, Zioupos P. Mechanical properties and the hierarchical structure of bone. Med Eng Phys. 1998; 20: 92-102.
- Webster D, Schulte FA, Lambers FM, Kuhn G, Müller R. Strain energy density gradients in bone marrow predict osteoblast and osteoclast activity: a finite element study. J Biomech. 2015; 48: 866-874.
- Florio CS. Development and implementation of a coupled computational muscle force optimization bone shape adaptation modeling method. Int J Numer Method Biomed Eng. 2015.
- Colloca M, Blanchard R, Hellmich C, Ito K, van Rietbergen B. A multiscale analytical approach for bone remodeling simulations: linking scales from collagen to trabeculae. Bone. 2014; 64: 303-313.
- Caouette C, Bureau MN, Vendittoli PA, Lavigne M, Nuño N. Anisotropic bone remodeling of a biomimetic metal-on-metal hip resurfacing implant. Med Eng Phys. 2012; 34: 559-565.
- Sumner DR. Long-term implant fixation and stress-shielding in total hip replacement. J Biomech. 2015; 48: 797-800.
- Podshivalov L, Anath Fischer, Pinhas Z Bar-Yoseph. On the Road to Personalized Medicine: Multiscale Computational Modeling of Bone Tissue. Arch Computat Methods Eng. 2014; 21: 399-479.