Dervishi A

Research Article

Austin J Biotechnol Bioeng. 2017; 4(3): 1081.

Cumulative Mean of the Laboratory Tests on Risk Prediction Model for Adult Intensive Care Patients

Dervishi A*

Data Scientist, Germany

*Corresponding author: Albion Devarshi, Data Scientist, Berliner Str.27d, Lutherstadt 06886, Germany

Received: June 16, 2017; Accepted: October 27, 2017; Published: November 03, 2017

Abstract

Purpose: The decisions clinicians make in Intensive Care Units (ICUs) should take account of the risks faced by individual patients. ICU patients with abnormalities in particular clinical parameters have been shown to have a higher risk of mortality. The goal of this study was to determine whether the results of cumulative mean of laboratory tests, which are commonly carried out on patients during ICU treatment, might be useful predictors of mortality risk within the ICU.

Methods: A total of 16,691 unique ICU adult patients (mortality 14.1%) were selected from MIMIC-III v1.3 public databases for this study. Data for each of the patients, who were aged 15–89 years, included cumulative mean values of bicarbonate, chloride, lactate, albumin, BUN, creatinine, sodium, white blood cell (WBC), PCO₂, and bilirubin tests, as well as their age and mortality outcome. Mortality risk prediction estimates and risk strata were developed using an iterative approach involving multivariable logistic regression. Machine learning, involving a non-parametric class of regression trees, was used for model selection.

Results: The Area Under the Receiver Operating Characteristics Curves (AUROC) was 0.84 with sensitivity and specificity values of 0.739 and 0.783, respectively. The Hosmer-Lemeshow goodness of fit test p-value was 0.906 for the best model.

Conclusion: Retrospective data, collected for unselected adult patients in the MIMIC databases, allowed good predictions of risks to individuals in critical care. Stratification and risk scores applied to the general ICU patient population could assist physicians in clinical decision making. Further studies need to evaluate the impact, on clinical outcomes, of using this model.

Keywords: ICU prognostic parameters; Decision support; Risk stratification; Mortality risk prediction; Linear regression

Introduction

Health-related data have been found to be helpful for assessing the risks faced by patients in Intensive Care Units (ICUs) [1-3]. Data mining, within the large amounts of clinical information collected in ICUs, has the potential to improve patients’ care and reduce the costs of treatment. This study used retrospective data to build a risk stratification model for ICU patients [4-7].

Laboratory tests are routinely carried out within hospitals to establish and clarify diagnoses or explain specific clinical conditions. Healthcare datasets contain results from previous tests, and may be useful for risk assessment because they give some indication of disease severity [8,9]. The identification of patterns in data from laboratory tests can help with the recognition of trends in the severity of the illnesses of patients in intensive care units [10,11].

During our data mining, we identified a number of clinical parameters that affect mortality rates within ICUs. Our data set included information on patients’ ages and Lengths of Stay in intensive care (LOS).

Our study focused on exploring the cumulative mean values of the results of laboratory tests carried out on patients in critical care. We examined 25 clinical parameters estimated by these tests. We concentrated on identifying variables that were important predictors of ICU mortality outcomes. Our aim in this study was to estimate the importance of the mean values of each of the laboratory tests and also their significance as predictive clinical parameters for use in models of risk within intensive care units.

Materials and Methods

The Medical Information Mart for Intensive Care III is a freely available database. It contains information on patients who stayed in the critical care units of the Beth Israel Deaconess Medical Center between 2001 and 2012.

The MIMIC III records contain: monitoring data, fluid input, output records, laboratory test results, procedure orders, text notes, mortality outcomes and demographics. The data cover 38,597 distinct adult patients and 49,785 hospital admissions. For our study, we selected 16,691 adult patients with ages between 15 and 89 years (mean = 63.4 years). The MIMIC III database has an overall ICU/in-hospital mortality rate of 11.5%; in the subset we used this increased to 14.1% [10]. The selection of patients from the database was based on the selection of unique patients were performed 28 laboratory analysis during their treatment. For each unique patient, the cumulative mean value was measured over the entire period of treatment in the ICU, until the patient left the ICU (survival) or died (non-survival). Throughout this project, we did not consider the cause of ICU admission, or the morbidity, comorbidity or demographic characteristics of the patients.

The data were analyzed by multiple logistic regressions; clinical predictors were used as explanatory variables (cumulative laboratory mean) and the response variable was mortality outcome in the ICU/ hospital. Figure 1 shows the relative importance of each variable [12- 14]. The clinical parameters that have most important contribution to modeling the data have the largest coefficient magnitudes and were used for construction model data. Eleven variables were included in the final multivariate model.

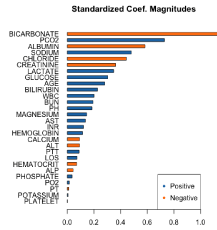
Figure 1: The importance of 28 clinical predictors in a multiple logistic regression analysis of ICU/Hospital mortality. The y-axis lists the variables in order of importance; the x-axis shows the magnitudes of their standardized coefficients.

    
    
    Figure 1:  The importance of 28 clinical predictors in a multiple logistic
regression analysis of ICU/Hospital mortality. The y-axis lists the variables in
order of importance; the x-axis shows the magnitudes of their standardized
coefficients.

Development of the Model

Multiple logistic regressions was used to develop the risk stratification. The multiple logistic regression model is as follows:

Logit=β₀+ β₁X₁ + • • • + β₁₁X₁₁

Here patients who did not survive are coded 1 and those who did survive are coded 0. Logit indicates the natural log of the odds ratio. The parameters (β_i) are effects on mortality outcome: β₀ is the intercept for the model, β₁through Β₁₁represent the model parameters corresponding to clinical predictors X₁ to X₁₁.

Predicted mortality risk scores were compared with observed outcomes. These data were used for model validation and risk stratification analysis.

Development of algorithm for levels selection

Machine learning algorithms assisted us in the risk level classification. There are many studies in which conditional inference trees (C-tree) or similar algorithms are used for selection and prediction of risk levels [15]. Based on our model data outcome and discrimination values, we trained the model, which was then used to generate risk levels.

Model Verification and Validation

The performance of our model was evaluated using measures of calibration and discrimination. For calibration, we used the Hosmer-Lemeshow test. This measures a model’s ability to generate predictions that are, on average, close to the average observed outcome. We considered the results of this test to be significant if the p-value was less than 0.05. Therefore, if a model had an associated p-value > 0.05, the null hypothesis that it adequately fit the data was not rejected [11,12].

The Area Under the Receiver Operating Characteristics curves (AUROC) is a popular statistical tool for characterizing the discriminating power of a classifier [13,14]. We used ROC curve analysis to assess the accuracy of the multiple logistic regression model categorizing individuals as surviving or not surviving ICU treatment.

The area under the ROC curve can range between 0.5 and 1, where 0.5 indicates a poor classifier and 1 means an excellent classifier. Valuable discrimination is suggested by ROC values of 0.7–0.8, and good discrimination by values exceeding 0.8. ROC curves are also used to test the prognostic significance of models to compare their predictive value [14] (Figure 2).

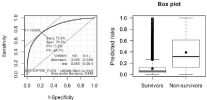
Figure 2: A ROC Receiver Operating Characteristic (ROC) curve for the model outcome. In our model, area under the curve is 0.84b Boxplot shows the distributions of the predicted probabilities per outcome value for Survivors vs. Non survivors among ICU patients in the model data: graphical impression of discrimination. The boxes show the 25%, 50% and 75% cumulative frequencies. The terminal lines show the 10% and 90% cumulative frequencies.

    
    
    Figure 2:  A ROC Receiver Operating Characteristic (ROC) curve for
the model outcome. In our model, area under the curve is 0.84b Boxplot
shows the distributions of the predicted probabilities per outcome value
for Survivors vs. Non survivors among ICU patients in the model data:
graphical impression of discrimination. The boxes show the 25%, 50% and
75% cumulative frequencies. The terminal lines show the 10% and 90%
cumulative frequencies.

Boxplot shows the distributions of the predicted probabilities per outcome value for Survivors vs. Non survivors among ICU patients in the model data: graphical impression of discrimination. The boxes show the 25%, 50% and 75% cumulative frequencies. The terminal lines show the 10% and 90% cumulative frequencies

Results

The 11 variables (cumulative mean) with the largest magnitude standardized coefficients in the multiple logistic regression modeling were used to build a model with fewer explanatory variables, improving the discriminatory power and accuracy of the model [15- 20].

We found that particular laboratory tests, and also groups of tests, had important predictive value for identifying patients at risk of death in the ICU/ hospital.

The cumulative mean values for patients who survived were compared with those for people who did not survive and found to be significantly different (p < 0.0001) for almost all variables (Table 1 & Figure 3).

Table 4: Values of 11 important characteristics for patients who survived or did not survive their time in the ICU.




  
     
    Non-Survivors
    Survivors
    p-value
  
  
    Patients
    2360
    14331
     
  
  
    Bicarbonate
     
     
  
  
    Mean±s.d.
    22.63±4.74
    25.66±3.26
    <0.0001
  
  
    Chloride
     
     
     
  
  
    Mean±s.d.
    104.94±6.00
    103.75±3.94
    <0.0001
  
  
    Albumin
     
     
     
  
  
    Mean±s.d.
    2.79±0.62
    3.30±0.64
    <0.0001
  
  
    Lactate
     
     
     
  
  
    Mean±s.d.
    3.63+3.08
    2.09±1.24
    <0.0001
  
  
    Sodium
     
     
     
  
  
    Mean±s.d.
    139.13±4.84
    138.62    ±3.04
    <0.0001
  
  
    WBC
     
     
     
  
  
    Mean±s.d.
    13.59±7.51
    10.66±4.36
    <0.0001
  
  
    BUN
     
     
     
  
  
    Mean±s.d.
    38.41±23.69
    25.79±16.38
    <0.0001
  
  
    PCO₂
     
     
     
  
  
    Mean±s.d.
    40.62±9.48
    41.12±7.54
    0.0145
  
  
    Creatinine
     
     
     
  
  
    Mean±s.d.
    1.79±1.37
    1.39±1.32
    <0.0001
  
  
    AGE
     
     
     
  
  
    Mean±s.d.
    67.24±15.53
    62.76±15.69
    <0.0001
  
  
    Bilirubin
     
     
     
  
  
    Mean±s.d.
    1.76±2.02
    0.94±1.10
    <0.0001
  
  
    Mean values and    standard deviations of blood bicarbonate levels (mEq/L); blood chloride    levels (mEq/L); blood albumin levels (g/dL); blood lactate levels (mmol/L);    blood sodium levels (mEq/L); blood WBC (K/uL); blood BUN levels (mg/dL);    blood PCO₂levels mm Hg); blood creatinine levels (mg/dL); age (years);    blood total bilirubin levels (mg/dL). The p-values indicate the significance    of the differences between the surviving and non-surviving patients.



Table 4: Values of 11 important characteristics for patients who survived or did
not survive their time in the ICU.

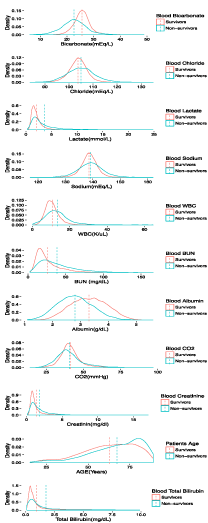
Figure 3: Distributions and cumulative mean values of the clinical variables for ICU survivors and non survivors.

    
    
    Figure 3:  Distributions and cumulative mean values of the clinical variables
for ICU survivors and non survivors.

Receiver Operator Characteristic (ROC) curves are commonly used to present discrimination results for binary decision problems in multiple linear regressions. Our model produced a value of 0.84with sensitivity and specificity values of 0.739 and 0.783 (Tables 2 and 3).

Table 2: Parameter estimates from the logistic regression.




  
    Variable 
    Estimate 
    Standard Error 
    (95% C) 
      2.5% 
    (95% CI) 
      97.5% 
    p value 
  
  
    (Intercept)
    -8.007
    1.053
    -10.074
    -5.946
    < 0.0001
  
  
    Albumin
    -0.904
    0.047
    -1.004
    -0.816
    < 0.0001
  
  
    Creatinine
    -0.375
    0.034
    -0.444
    -0.310
    < 0.0001
  
  
    Bicarbonate
    -0.367
    0.015
    -0.398
    -0.337
    < 0.0001
  
  
    Chloride
    -0.167
    0.015
    -0.199
    -0.137
    < 0.0001
  
  
    BUN
    0.017
    0.001
    0.013
    0.020
    < 0.0001
  
  
    Age
    0.019
    0.001
    0.015
    0.023
    < 0.0001
  
  
    WBC
    0.042
    0.004
    0.033
    0.052
    < 0.0001
  
  
    PCO₂
    0.080
    0.004
    0.072
    0.089
    < 0.0001 
  
  
    Bilirubin
    0.174
    0.017
    0.140
    0.208
    < 0.0001 
  
  
    Lactate
    0.201
    0.016
    0.168
    0.231
    < 0.0001 
  
  
    Sodium
    0.213
    0.017
    0.180
    0.248
    < 0.0001



Table 2: Parameter estimates from the logistic regression.

Table 3: Assessment of the goodness-of-fit of the logistic regression model by Hosmer Lemes how test on its predictions.




  
    Risk bands 
      in % 
    Total 
    Mean Predicted 
    Mean Observed 
    Predicted 
    Observed 
  
  
    = 0 to < 2
    1670
    0.012
    0.013
    19.51
    21
  
  
    = 2 to < 3
    1669
    0.022
    0.022
    36.88
    36
  
  
    = 3 to < 4
    1669
    0.032
    0.032
    54.23
    54
  
  
    = 4 to < 5
    1669
    0.045
    0.040
    74.85
    66
  
  
    = 6 to < 8
    1669
    0.060
    0.064
    100.92
    106
  
  
    = 8 to < 11
    1669
    0.081
    0.083
    135.92
    138
  
  
    = 11 to < 15
    1669
    0.112
    0.108
    186.63
    180
  
  
    = 15 to < 25
    1669
    0.162
    0.154
    270.62
    257
  
  
    = 25 to < 60
    1669
    0.267
    0.270
    446.17
    451
  
  
    = 60
    1669
    0.620
    0.630
    1034.27
    1051
  
  
    ?²=    3.4057, df = 8, p-value = 0.9064



Table 3: Assessment of the goodness-of-fit of the logistic regression model by
Hosmer Lemes how test on its predictions.

However, our model validation was carried out independently from the model classification results to build a confusion matrix and report classification accuracy. The confusion matrix was constructed with the Caret library in R. Overall classification accuracy was 0.89 (95% CI: (0.88, 0.90).

The most significant prognostic split (p <0.001) was based on the risk score and divided the mortality risk into five levels (Table 4 and Figure 4).

Table 4: Risk levels based on percentage mortality prediction.




  
    Risk Stratification 
    Mortality Risk 
  
  
    Very Low Risk 
    <6%
  
  
    Low Risk 
    <12%
  
  
    Medium Risk 
    <18%
  
  
    High Risk 
    <24%
  
  
    Very High Risk 
    ³24%



Table 4: Risk levels based on percentage mortality prediction.

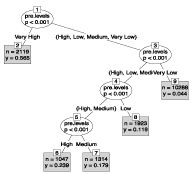
Figure 4: Displays the C-tree-based models for the risk levels selection/ mortality outcome.

    
    
    Figure 4:  Displays the C-tree-based models for the risk levels selection/
mortality outcome.

In the Very Low risk level group that is at node 9 the risk of mortality was 4.4%: 44 people were reported dead out of a total of 1000 people in this node. For the Low levels of risk group node (8), the probability of mortality was 11.9%. The Low Medium of risk group is node (7), with a risk of mortality of 17.9%. The High level of risk group is node (6), their probability of mortality was 23.9%: For the Very High level of risk group, at node (2), the risk of mortality was 56% [21-26].

We used a combination of multiple algorithms using forest floor visualization to show the relation with mortality risk probability and cumulative mean laboratory values (Figure 5).

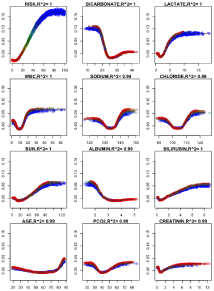
Figure 5: Plots arranged according to variable importance.

    
    
    Figure 5:  Plots arranged according to variable importance.

The prediction of the Multiple logistic regression for the cumulative mean of the laboratory tests as model predictors revealed that: Bicarbonate (OR: 0.69, 95% CI: 0.67-0.71) has coefficient of determination r²=1 on relationship with risk. The mortality risk increases up to 10% probability change when values vary from 23-30 mEq/L.

The lactate (OR: 0.84, 95% CI: 0.82-0.87) has coefficient of determination r²=1 on relationship with risk. When lactate cumulative mean change values above 2.2 mmol/L levels of risk increase up to 10%.

The WBC (OR: 1.04, 95% CI: 1.03-1.05), r²=1. When WBC cumulative mean change from 4.0-12 K/uL levels of risk probability increases up to 7%.

The sodium (OR: 1.23, 95% CI: 1.19-1.28) and chloride (OR:0.84, 95% CI: 0.82-0.87) both have coefficient of determination r²=0.99 on relationship with risk. When cumulative mean values change for sodium 135-142 mEq/L and chloride 97-107 mEq/L levels of mortality risk probability increases up to 7%.

The BUN (OR: 1.01, 95% CI: 1.0-1.02) and bilirubin (OR: 1.19, 95% CI: 1.15-1.23) both has coefficient of determination r²=1 on relationship with risk. When cumulative mean values change for BUN 7-20 mg/dL and bilirubin 0.3-1.9 mg/dL levels of risk probability increases up to 7%.

The albumin (OR: 0.40, 95% CI: 0.36-0.44) has coefficient of determination r²=0.99 on relationship with risk. When cumulative mean values fall below 3.4 g/dL levels of risk probability increases up to 7%.

The age (OR: 1.01, 95% CI: 1.0-1.02) has coefficient of determination r²=0.99 on relationship with risk. Patients age over 75 years it was found to have more impact on mortality risk and probability increases up to 5%.

The PCO₂ (OR: 1.08, 95% CI: 1.07-1.09) has coefficient of determination r²=0.99 on relationship with risk. When blood PCO₂ cumulative mean change from 35-45 mmHg levels of mortality risk probability increases up to 4%.

The creatinine (OR: 0.68, 95% CI: 0.64-0.73) has coefficient of determination r²=0.99 on relationship with risk. When cumulative mean values increase over 1.2 mg/dL levels of mortality risk probability increases up to 3% [16,17,27] (Figure 5).

The X-axes are the model predictor’s values and mortality risk probability in percentage. The Y-axes are cross-validation feature contributions (predicted probability upon model predictor’s values).

Color gradient in all plots is parallel to the mortality risk probability in percentage; redrepresent is minimal mortality risk and blue maximal mortality risk. R2 quantifies the goodness-of-fit when visualizing the clinical parameter effect as on the risk score.

The eleven cumulative mean laboratory values had a non-linear relationship in a relation with mortality risk probability (Figure 6).

The cumulative mean of bicarbonate values was found to have a Sigmoid-shaped negatively perceived relationship with the ICU mortality risk. The minimum values of the cumulative mean of bicarbonate with the least mortality risk probability were found to be 27 mEq/l. Higher is the cumulative mean of bicarbonate values the less is the probability for ICU mortality rate.

The cumulative mean of lactate values is positively perceived Sigmoid-shaped curve the relationship with the ICU mortality risk. The minimum values of the cumulative mean of lactate with the least mortality risk probability were found to be 1.5 mmol/L.

The cumulative mean of WBC is positively perceived Sigmoidshaped curve the relationship with the ICU mortality risk. However, the shape of the curve was decelerated in the 50th percentile and 8.8 K/uL was minimum values of the cumulative mean of WBC with the least mortality risk.

The cumulative mean of the sodium and chloride were in the U-shaped curve with the shallow slope with deceleration 25-30th percentile in a relationship for the mortality risk. While minimum values of the cumulative mean for the least mortality risk for sodium is 138.1 mEq/L and chloride 102.2 mEq/L.

The cumulative mean of Bun and bilirubin has linear trend lines increased probability in the relationship with the mortality risk. The minimum values for least mortality risk were for Bun 15.7 mg/dL and bilirubin 0.66 mg/dL.

The cumulative mean of albumin values is negatively perceived exponential curve in the relationship with the ICU mortality risk. The minimum values of the cumulative mean of albumin with the least mortality risk probability were found to be 4.0 g/dL.

The cumulative mean of age measured in years has linear trend lines increased probability in the relationship with the mortality risk. However, the shape of the curve was decelerated in the 25th percentile and 39 years was minimum values of the cumulative mean of WBC with the least mortality risk.

The cumulative mean of PCO₂ measured in years has sine wave in the relationship with the mortality risk. The minimum values of the cumulative mean of PCO₂ with the least mortality risk probability were found to be 40.5 mmHg.

The cumulative mean of creatinine levels has a peak on 25th percentile in the range of creatinine levels 3-4 mg/dL, while the minimum value of the cumulative mean is 1.0 mg/dL.

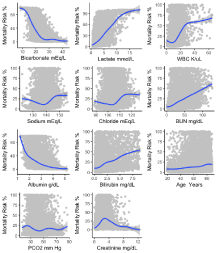
Figure 6: Generalized Additive Model (GAM) with smooth functions of predictor variables used for visualization of cumulative laboratory values where you can see these nonlinearities between risk scores.

    
    
    Figure 6:  Generalized Additive Model (GAM) with smooth functions of
predictor variables used for visualization of cumulative laboratory values
where you can see these nonlinearities between risk scores.

Discussion

Risk adjustment scoring and predicting outcomes by using laboratory tests to predict mortality in combination with clinical assessment is well established in the critical care literature [18,19]. There are multiple studies that report linearly proportional associations between laboratory tests disorders, age, LOS, multiple morbidities, comorbidities and mortality outcomes [20-24]. However, this model was built to assess the importance of the cumulative mean values of laboratory tests and their importance to predictive values in risk adjustment.

The use of selected laboratory tests to predict ICU mortality is not meant to aid the clinicians because treatment is disease-specific. However, we think that the majority of the mortality risk is not directly associated with the imbalance in laboratory tests itself, but rather the clinical situation in which the abnormalities occurred.

Although, during ICU patient treatment regarding imbalance in laboratory tests and background of disease the cumulative mean values show predictive value in prediction of mortality risk.

Based on our findings, predictive values for cumulative laboratory mean values in ICU as clinical parameters can be generalized to all adult critical care patients without the need for differentiations such as demographic variables, the type of admission to the Medical- Surgical ICU, or morbidity and comorbidity.

Moreover, there is widespread recognition that abnormal laboratory tests are associated with greater risks of harm. While statistics are necessary for clinicians to give a quantitative or predictive estimate of risk stratification, mortality risk prediction and the immediate detection of clinical trends can support clinical decisions and improve patient survival [25,26]. Nowadays, advanced statistical software gives us the ability to build applications based on particular models. Similar applications could be incorporated into an early warning system within general medical software. Such applications have the potential to help clinicians learn what patterns of test results indicate risks early in their development.

The model web application

The Shiny package of R gives an opportunity for exploring interactive data visualization, particularly within web browsers. In this paper, we set out to demonstrate the possibility of creating a dynamic application for risk adjustment and stratification in adult ICU patients. Using the slider input widget in the application, we selected the labs and age values. The algorithm calculates odds, model risk score and risk level for each unit change of model predictor. The interactive Shiny application for this model can be accessed with the following URL: https://albiondervishi.shinyapps.io/Stratification/.

Conclusion

We conducted a study of 16,691 ICU patients and found that several specific laboratory tests in regarding cumulative mean that had good predictive value for identifying at-risk individuals among critically ill patients.

The results of our study show that cumulative mean of bicarbonate, chloride, lactate, albumin, BUN, creatinine, sodium, WBC, PCO₂ and bilirubin levels can be used as predictors in risk assessments for the ICU patient population.

We calculated an approximate percentage mortality risk for each unit of change and can reliably predict outcomes, particularly for mortality risk score and risk levels. While randomized controlled studies and large international data sets from different hospitals and countries are needed to draw firm conclusions, the present study may contribute to understanding the risks indicated by these important clinical parameters, and enable their utilization in clinical practice.

References

Download PDF

Citation: Dervishi A. Cumulative Mean of the Laboratory Tests on Risk Prediction Model for Adult Intensive Care Patients. Austin J Biotechnol Bioeng. 2017; 4(3): 1081. ISSN:2378-3036

Instruction for Authors

Submit Your Article

Risk Stratification	Mortality Risk
Very Low Risk	<6%
Low Risk	<12%
Medium Risk	<18%
High Risk	<24%
Very High Risk	³24%