Trajectory and Transit Patterns of Isolated Nanoparticles in Structured Micromodels

Research Article

Austin J Chem Eng. 2014;1(2): 1006.

Trajectory and Transit Patterns of Isolated Nanoparticles in Structured Micromodels

Sajjadiani S1, Javadpour F2 and Jeje AA1*

1Department of Chemical and Petroleum Engineering, University of Calgary, Canada

2Department of Geosciences, University of Texas, USA

*Corresponding author: Jeje AA, Department of Chemical and Petroleum Engineering, Schulich School of Engineering, University of Calgary, Calgary, AB T2N 1N4, Canada

Received: May 30, 2014; Accepted: July 09, 2014; Published: July 14, 2014

Abstract

Transport of suspensions of ultrafine and colloidal particles through porous structures is a common occurrence. Often, of interest is how far the particles would penetrate into the structure on advective streams. Experiments were conducted to record the paths of nano particles in dilute suspensions through micro models of porous media. The particles are primarily propelled by hydrodynamic forces through regular arrays of cylindrical posts arranged between two closely-spaced flat surfaces. The setup consisted of the test cell, an inverted microscope, a high speed camera, a data processor, a precise actuating syringe pump, and spherical silica particles (0.2, 0.5 and 1.5 μm diameter) that encapsulated a fluorescent dye. The particle trajectories deviated from the streamlines for particle-free fluids through the domain, and the slip condition was prevalent in an environment in which the fluid velocity field and the particle motion affected each other. The trajectories show evidence of Brownian motion more significantly for the smaller particles that were also dispersed faster through the less porous media.

Keywords: Particle trajectory; Porous media; Axial dispersion

Abbreviations

COMSOL; PDMS; SCMOS; s; ms; μm; mm; kg/m3; v/v; ml; Re; Re+; Pe; μm/s; m2/s

Introduction

Observations on the paths travelled by nano particles in dilute suspensions, as they are conveyed through models of porous media, are reported in this study. Suspensions of solid particles and liquid droplets in fluids are ubiquitous. As an example, the air we breathe supports numerous microorganisms, viruses, silica, smoke and salt particles, and mist and fog in concentrations that vary with location, time and prevailing conditions such as wind, temperature, humidity and sources of release or production. Concentrations of these particles in air are typically low on a volume fraction basis. On inhalation, such suspended particles pass through and may be captured within the bifurcating generations of narrowing tubes constituting the airways of the lung, a structured porous medium [1].

Physical analogs of porous media with migratory particles abound. Catalytic reactors, hydrocarbon reservoirs and aquifers are systems through the pores of which fine particles are normally displaced and produced with the flowing fluid. As a corollary, tiny tracer particles are injected into porous media to identify potential migration paths of pollutants and contaminants from industrial surface operations or piles of wastes [2]. In the petroleum industry, potential exists to degrade heavy oils and bitumen in-situ, under reservoir conditions, if particles of appropriate catalysts can be transported into partially saturated formations. Commercial and domestic systems and processes involving particles carried in streams through porous bodies include deep-bed filtration in granular or fibrous beds such as in household furnace filters or packed beds for removing white blood cells from platelet-rich-plasma prior to transfusion [3]. It is of interest to identify factors that regulate the rates of particle movements in the conveying fluid, the paths and distances the particles travel, and axial dispersion of the particles as might be correlated to the structures of the porous media to provide the technical foundation for the design of processes or an understanding of the performance characteristics of systems such as described in the foregoing.

The typical porous medium is a complex structure of pores and cavities within arrangements of irregular and opaque particles or fiber strands. Tracking submicron and colloidal particles through such geometry is not often feasible and investigators have attempted to understand the dynamics by resorting to computer simulations [4] and experimental micro models [5]. Geometrically, micro models are two-dimensional representations or thin sections of a porous medium mounted within parallel optically-clear plates. Such an arrangement allows visual observation of fluid flow and particle movement in the interstices between solid elements, and the displacement of one fluid by another. In situations when interfaces are present between immiscible fluids in the medium, the fluid moves in response to local capillary forces and applied pressure. At the macro-scale level, for immiscible displacement, flow through the domain is spatially integrated at the front, even if unstable, and the displacement qualifies as 2-dimensional flow [6]. When particles smaller than the pores are in suspension and their movements are to be tracked, as is of current interest, the flow of the suspending fluid (assumed not a low pressure gas) is described at the microscopic level and the Navier-Stokes equations are applicable. At the pore-level scale, the flow is 3-dimensional for single fluids and miscible displacement, but the irregular and uneven internal boundaries for the flow are difficult to characterize. Generalizations about the local flow dynamics, and influences on particles in motion, are not easy to arrive at unless the structures within the media are regular. It is for these reasons that micro models are often designed as organized arrays of short cylindrical post, typically in triangular or rectangular layout, between two parallel transparent plates.

Highly porous filters are modeled as an ensemble of cylinders acting as collectors [7] or as arrays of infinitely long cylinders oriented parallel or normal to the direction of fluid flow [8,9]. In micro fluidic devices, flow through regular arrays or around cylinders has found application for the separation of particles by size [10]. Simulations have been carried out to predict trajectories for suspended particles but there have been few experimental results to provide validation. A micro-model is valuable for observing and tracking particles [11] but sufficient attention has not been paid to the influence of the flow patterns in the conveying fluid. Di Carlo et al. [10] have reported that fluid and particles interact to cause particles to follow paths unanticipated in micro channels.

Materials and Methods

The apparatus

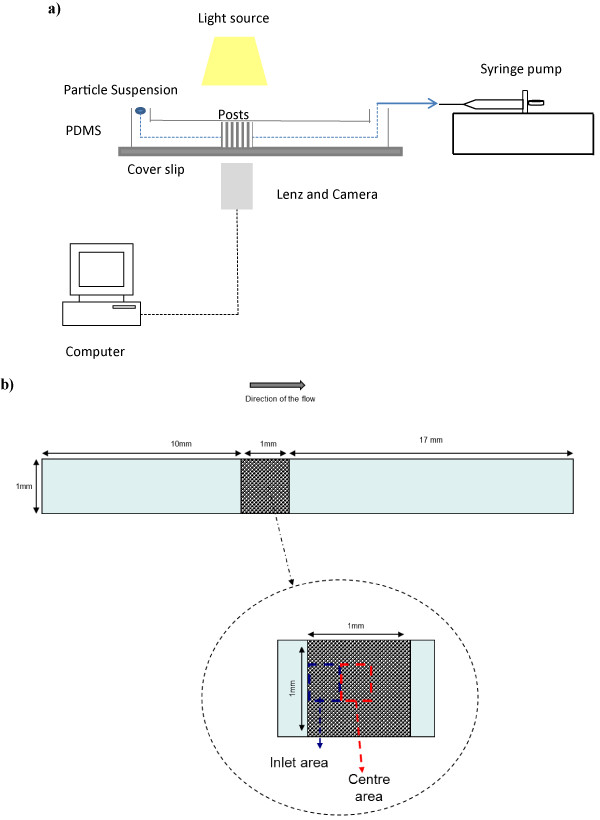
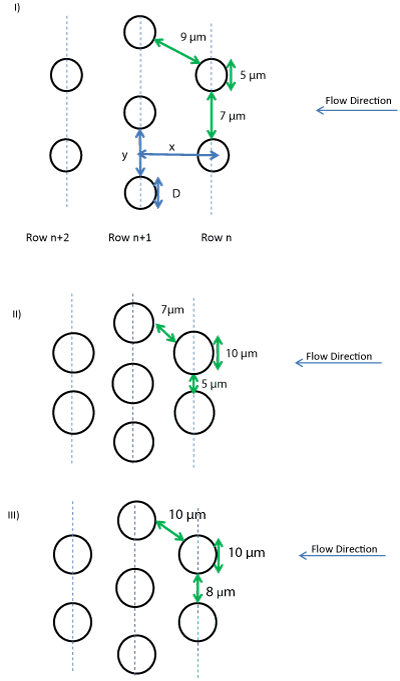
A schematic of the experimental set up is shown in (Figure 1a). It consists of four components; the test cell, an inverted microscope, image recording and storage devices and an actuating pump. The test cell, viewed from above, is shown in (Figure 1b). It comprises a rectangular channel between two parallel plates that are 28 mm long and 1 mm wide. The spacing between the plates is 20 μm. The bottom plate with sides is fabricated from poly-di-methyl siloxane (PDMS) from silicon wafer molds that have cylindrical holes etched in a region in prescribed patterns by soft lithographic methods [12]. When cured and stripped from the mold, the clear polymer becomes the bottom plate and side walls. A section of the plate has cylindrical posts that are 5 or 10 μm in diameter and uniformly20 μm long projecting out. The posts are in triangular arrays in this study and are within a 1 x 1 mm square area, as shown in (Figure 1b). The top plate of the test cell is a glass cover slip, with injection and withdrawal ports pre-drilled through. The micro model of a porous medium is where the posts are located; and the 10 and 17 mm long sections on either side of this area constitute Hele-Shaw cells through which flows stabilize before entering and after leaving the micro model. Sketches of the arrays of the posts are in (Figure 2a-c). The arrays are identified as configurations I, II and III in subsequent references. It is important to note that the axes of the posts do not form vertices of equilateral triangles. Test cell parameters are listed in Table 1. The solid density is the fraction of the test section occupied by the posts, or 1 minus the porosity. The values were between 0.13 and 0.35 for the configurations. For a typical porous medium, areas ascribed to the bounding walls (if present) are negligible fractions of the total surface area exposed to contacting fluids. This is not the case for the micro models in Table1. Contributions of the bounding surfaces to the observed velocity field that developed and to the viscous resistance to flow in the system cannot be dismissed.

Figure 1 :Schematic diagrams of the micromodel setup. (a) The apparatus consists of the test cell, a syringe pump, an inverted light microscope, a high speed camera and a computer. (b)Schematic diagram of the test cell,top view.






Figure 1 : Schematic diagrams of the micromodel setup. (a) The apparatus consists of the test cell, a syringe pump, an inverted light microscope, a high speed camera and a computer. (b)Schematic diagram of the test cell,top view.

Figure 2 :The configurations for the micromodels, in triangular arrays.






Figure 2 : The configurations for the micromodels, in triangular arrays.

The second component of the setup is an inverted light microscope (ZEISS / AXIOVERT 200, 40 Lens: plan-Apochromat 40X/1.4 oil) equipped with a high speed digital camera (Andor Neo, SCMOS). The objective was focused at the mid-plane of the test cell. The depth of field was ~ 10 μm and the field of view was 895 x 850 μm. The high speed camera was operated at a frame rate of 30 per second and 25 ms exposures. Both the camera and a computer constitute the image capture and storage devices. The fourth piece of the apparatus is a calibrated syringe pump (model 341B, SAGE Instruments) for drawing fluid at constant volumetric rates out of the test cell. The cells were previously cleaned and saturated with deionised water at room temperature, density ~ 1000 kg/m3.

The particles used were spherical silica particles encapsulating a fluorescent green dye (Microspheres-Nanospheres). The surfaces were electrically neutral. The density was 1443 kg/m3 and the diameters were 0.2, 0.5 and 1.5 μm. Particles in the size range used are at or below the resolution limits for optical microscopes, hence the dye trapped within. When exposed to light of an appropriate frequency, the trapped dye fluoresces and thus allows the particles to be located. Fluorophores, however, undergo photon-induced chemical damage and covalent modification leading to fading and ultimately loss of the ability to be excited on continuous exposure to light. This phenomenon is photo bleaching. The dye in the silica particles used required 3-4 minutes of continuous illumination to start fading and over 5 minutes to be un excitable. Photo bleaching did not occur for runs lasting less than 2 minutes.

Since the particles are denser than water, the prospect of gravity displacing particles from the focus of the microscope was considered. Settling was only detected in particle suspensions in a Ultraviolet- Visible light spectrometer only after 20 minutes. Particles moved through the field of view in 15 to 120 seconds. Of importance also was that there were no agglomerates. The 5% v/v suspensions purchased were subjected to ultrasonic vibrations to dissociate clusters before being diluted to concentrations of ~ 108 per ml. At this concentration, particles moved singly.

Presented in Table 2 are the flow conditions. Three different flow rates give superficial (and thus average) velocities of 6.13, 14.88 and 54.68 μm/s at any cross-section of the channel. The corresponding pore velocities and the Reynolds numbers relative to the diameters of the posts of the test sections are also shown in the table. The Reynolds numbers are less than 2x10-3.

Experiments

Each test cell was thoroughly cleaned with at least five pore volumes of ethanol to remove any traces of PDMS. Fifteen pore volumes of deionised water were pulled through to displace and remove the alcohol. The test cell was, after this, completely saturated with deionised water under a partial vacuum to ensure there were no bubbles in the system. Water, pulled into the cell at a prescribed rate, was replaced by a prepared suspension with the flow rate maintained constant. Particles trajectories in the micro models were observed and recorded. The system temperature was relatively constant at 20±2°C.

Results and Discussion

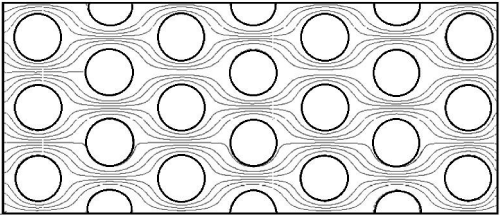
(Figure 3) shows streamlines for particle-free liquid in creeping flow normal to an array of posts, as calculated and plotted on COMSOL for the micro model configuration II (Table 1). In the simulation, the posts were parallel and infinitely long. Similar plots were generated for the other two configurations. At very low Reynolds numbers, the shape of the contours of the streamlines is invariant.

Figure 3 :Fluid streamlines around posts for micro model configuration II, generated by COMSOL.






Figure 3 : Fluid streamlines around posts for micro model configuration II, generated by COMSOL.

The dispersed phase

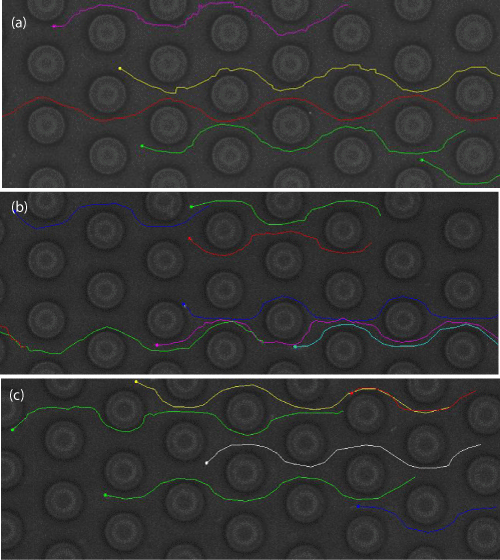
From experiments, representative trajectories of particles of different sizes and for different suspension flow rates for configuration II are shown in (Figures 4-6). The stream lines for the fluid in (Figures 3) and the lines joining prior positions of the particles, the streak lines in (Figures 4-6), are not coincident. First is that each particle appears to trace a unique path. From (Figure 2), a cycle is defined as the distance between rows n and n+2. The path tracked by a particle through any two consecutive cycles is different. Typically, a particle passing through the middle of the "pore" of row n moves relatively fast. It slows down and grazes the side of the post in the n+1 row, from either side, before accelerating to the next pore. It would seldom end up at the same position in the new pore as it had in the penultimate pore. Such apparent crossing of streamlines has been ascribed to inertial lift by Di Carlo et al. [10]. The streak lines show that any two particles that appeared to be initially on the same path diverged, even at the highest flow rate and for the larger particles. When a particle grazes a post, the traces of approach and departure are skewed on either side of the plane through the pore, indicating that the motion is not reversible. Random, high frequency, lateral displacements were experienced by all the particles. These were more noticeable as the particle size decreased. The foregoing observations would appear to have consequences for using finite-sized particles for flow visualization studies in micro fluidic devices and in micro models.

The trajectories traced in (Figures 4-6) were obtained by joining consecutive images of light-points of individual particles in motion. At the highest of the three flow rates, the particles were revealed as light streaks in each image frame. Corrected for magnification, the length of a streak divided by the exposure time, coupled with the direction, yielded an average local velocity at the streak's mid-point. In digital images, the accuracy of measuring the length of a streak is determined by the size of a pixel and errors were ~2%. Estimates of local particle speeds and the orientation of movement were obtained and are presented for the three micro model configurations and the three particle sizes at the highest flow rate of Table 2 in Figures (7-9).

Figure 4 :Samples of particle trajectory for 200 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension in(jebct)ion rates.






Figure 4 : Samples of particle trajectory for 200 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension in(jebct)ion rates.

Figure 5 :Samples of particle trajectory for 500 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension injection rates.






Figure 5 : Samples of particle trajectory for 500 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension injection rates.

Figure 6 :Samples of particle trajectory for 1500 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension injection rates.






Figure 6 : Samples of particle trajectory for 1500 nm diameter spherical silica particles in micro model configuration II at the (a) slow, (b) intermediate and (c) high suspension injection rates.

Patterns emerge from the data in (Figures 7-9). Local particle velocities are highest near or at the mid-point between adjacent posts in each row of posts oriented normal to the bulk flow. Velocities at such locations decreased as the particle sizes become smaller. Particles accelerated towards the constriction presented by the posts, the pores and decelerated rapidly once they emerged. Particle motion is restrained near posts as would be consistent with lower velocities within boundary layers. Variations in local particle velocities at different positions reflect but do not describe the velocity field for the fluid. Similar conclusions may be drawn for flow in more structurally complex porous media.

Figure 7 :Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration I at the high flow rate.






Figure 7 : Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration I at the high flow rate.

Figure 8 :Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration II at the high flow rate.






Figure 8 : Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration II at the high flow rate.

Figure 9 :Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration III at the high flow rate.






Figure 9 : Velocity vector plots for 200, 500 and 1,500 nm diameter silica particles in micromodel configuration III at the high flow rate.

It is informative to compare the above observations with prior work. The closest experimental work to the current study, in terms of tracking trajectories of particles passing through arrays of cylinders, is that reported by Kirsch and Fuchs [13]. In that study, particles apparently followed streamlines, and the local particle and fluid velocities are assumed equal. Current work involves much smaller spatial and time scales. The Reynolds numbers (with reference to the post diameter) for their study was one to two orders of magnitude higher (at 0.01 - 0.05) than herein. The tracking particles, 20-30 μm diameter spherical granules of poly methyl methacrylate coated with gold, were neutrally buoyant in the 95% glycerol liquid and were much smaller than the post diameters (7 and 14 mm). The volume fractions occupied by the posts in equilateral triangular arrays were 0.05 and 0.2. This means that separation between the posts in a row, the "pores", were 22.8 mm wide for the 7 mm diameter posts and 15.8 mm wide for the 14 mm diameter cylinders. The diameter of the tracking particles relative to the pore width was < 1/500 and was thus too small to significantly alter the fluid velocity profiles. These are in contrast to the conditions for the present study for which the particle diameter: pore width was in the range 1/16 to 1/3. The trajectories for the particles in Kirsch and Fuchs' Figure 3 indicate that the streamlines around the cylinders have substantially recovered to the patterns upstream of the cylinder at about ½ to 1 particle diameter downstream. In effect, for row separation of the order of one post diameter, the streamlines resemble those for flow around isolated cylinders at low Reynolds numbers.

Figure 10 :Velocity profile for creeping flow through a rectangular duct [17].






Figure 10 : Velocity profile for creeping flow through a rectangular duct [17].

Other recent experimental studies that involved tracking of particles in micro-models are those of Auset and Keller [11] and Baumann et al. [14]. Auset and Keller were interested in pore-scale effects of particle and pore sizes on colloidal dispersion in micro models. The micro models were quadrilateral arrays of rounded rectangular posts with straight, intersecting channels of constant 10 and 20 μm width separating the posts in two configurations, and a third configuration with both 10 and 20 μm channel width and paths that are not straight. The depth of the channels was 12 μm. The colloidal particles were 2,3,5 and 7 μm diameter, large enough to modify local flow patterns in the channels but not exhibit significant Brownian motion. The particles were also about 5% denser than water, the medium of suspension. The authors concluded that larger colloid particles were less dispersed than smaller ones because larger particles travelled in the center streamlines, at higher velocities, and with less detours. This appears to be a conjecture as neither the positions nor the instantaneous velocities of particles were reported. In this study, larger particles moved faster than smaller ones but either is just as likely to be anywhere in the domain and large particles doing not continuously follow fast streams. For micro model configuration 3 that they called the "zigzag network", particles are shown to have migrated from one side of a channel to the opposite side. This would require that streamlines are crossed rather than tracked. Particles that detoured into side channels appear to be moving, at upstream locations, close to a wall adjacent to the side streams into which they are diverted irrespective of pore size (as evident in their Figure 6).

Figure 11 :Dimensionless axial dispersion coefficient (KL/Di) versus Peclet number Pe for all experimental data.






Figure 11 : Dimensionless axial dispersion coefficient (KL/Di) versus Peclet number Pe for all experimental data.

Baumann et al.'s study on spreading of tracers in aquifers is similar to Auset and Keller's. The micro models constructed were ellipsoidal and cylindrical arrays with pore throats that were between 30 and 60 μm wide, and the channel depth was 50 μm. The micro model porosities were 0.26 to 0.36. Tracks of 0.5 and 1 μm diameter polystyrene microspheres in ionic media were recorded at 10 frames per second and the analysis done was on the path lengths traversed at the macro scale. Dispersivity of particles was reported to increase with ionic strength and decrease with colloid size.

Hydrodynamic forces propelled the particles in this study and the velocity field for the conveying fluid is important.

The continuous phase

Flow within each of the relatively simple micro model configurations of this study is complex, and the profiles are not readily amenable to analytical solutions. However, insight may be gained by exploring limiting solutions at two planes normal to the net flow direction. Two representative profiles, under conditions of reversibility and fully developed flows, are considered at the space between two adjacent posts in a row, "the pore", and at the mid-plane between two consecutive rows or grids, the "Hele-Shaw" approximation. At a plane through the axes of adjacent posts, flow is assumed to approximate that through a rectangular duct of a projection that is 5,7 or 8 μm wide and 20 μm tall. The fully developed velocity profile in a rectangular duct, for a viscous fluid, is [15,16]

The profile reproduced from Qu and Muwadar [17] in Figure (10) is for a rectangular section that is 180 x 60 μm. The pattern will be similar to flow through 5, 7 and 8 x 20 μm cross-sections. At the highest flow rate in Table (2) for micro model configuration I, the superficial velocity (volume rate / total cross-sectional area) into the micro-model is 54.68 μm/s, the average pore velocity U is calculated to be 93.7 μm/s, and the maximum velocity is estimated at 176.7 μm/s [18]. A comparison with the maximum particle velocities, at approximately the same locations in Figure (7, a, b and c), show that the fluid is faster than the particle at the center of the pore and thus would be dragging the particles forward towards the constriction. The situation seems reversed for particles close to the posts where they appear to be moving faster than the fluid. These observations are consistent with the analysis of Falade and Brenner [19] on the effect of wall curvature on Stoke's resistance. The largest of the particle sizes (1.5 μm diameter) has the highest local velocity of120.9 μm/s near the center of the pore. The velocities for the 0.5 and 0.2 μm particles were 107.4 and 100 μm/s respectively at similar locations.

A fully developed velocity profile as in equation (1) may be justified through an estimation of the order of magnitude of the entrance length into a rectangular duct [16]. For the micro model configuration I, the aspect ratio a (or b/a) equals 0.35, the hydraulic diameter of the opening Dh equals 10.37 μm and the Reynolds number Re+(ρUDh/μ) equals 9.72x10-4 at the highest flow rate. The entrance length Lhy into a rectangular duct has an estimated value of 8.34x10-4 μm. That is, velocity profiles develop over very short distances and the assumption is considered valid.

The velocity profile at the second plane is based on a more qualified reasoning. Downstream of a row of posts or grid, the fluid pattern adjusts. The fluid in the wake of posts accelerates while that emerging from the pores slows down while spreading laterally. Particle motions in (Figures 7-9) do reflect directional and speed changes. If it is assumed that the particles, because of the very low concentrations, do not substantially modify the profiles of the conveying fluid, fluid profiles through the mid-plane between two adjacent rows may be approximated, in the limit, with the Hele-Shaw results, i.e. a parabolic profile given by

where a is the half width of the gap separating the plates.

The velocity is maximum at y = 0 or along the mid-plane of the two bounding surfaces, and the value is 1.5 times the average velocity. Thus for configuration I, the maximum fluid velocity would be 82 μm/s. An inspection of (Figure 7), although not conclusive, would suggest that the particles are moving faster than the fluid at this location and are therefore experiencing deceleration due to hydrodynamic forces in the first half of the space between consecutive rows of posts. The foregoing are approximations for actual velocity profiles that have been calculated for viscous flow through arrays of parallel cylinders [6,20-27]. The wider the distances separating consecutive rows of an array, the closer would the foregoing approximate profile come to being realized at the mid-plane.

Brownian Motion and Axial Dispersion

Nano particles experience thermally fluctuations and, as a result, random displacements known as Brownian motion [28-30] in the suspending medium. This is reflected in the trace of particle positions in (Figures 4-6). Irregular and short-range, lateral displacements are noted along the paths of the particles. The degree of resolution of the fluctuations [31] is determined by the rate of image capture and magnification, in this case, 30 frames per second and a magnification of 100.The frequency and extent of displacements of the particles decreased as both the flow rates and particle size were increased.

Three parameters related to the paths for and the distribution of particles was evaluated from the data; the tortuosity, space-averaged axial velocities and axially-oriented translational dispersion. Each of these involved calculations for several particles. The tortuosity λ is the total actual distance a particle travels (along a smooth path) divided by the linear distance between the start and terminal locations. It scales with the rate of diffusion through the media [32]. The results for over 50 particles at each flow condition and particle size for micro-model configuration I are shown in Table 3. For this configuration, a maximum theoretical value for λ of 1.62 - 1.65 is estimated for a particle travelling through the middle of all pores on its route. Measured values in Table 6 are lower than this estimate, indicating that the paths were more "straight" and the larger particles experienced the least deviations. The maximum theoretical value for λ for configuration II, with the micro model with the lowest porosity is around 1.28.

The second parameter, the mean speeds at which particles percolate or pass through a porous medium, is often of more interest in technical operations. The average speed is the integrated value over at least a geometric cycle of the micro model. For the data reported in Table 4, each particle is observed to have travelled through four cycles. Both the linear distances Ls and actual tracks length La covered by particles was determined and divided by the time that elapsed for each of 35 to 45 particles. The results in Table 4 for VLs confirm that larger particles would penetrate deeper, over a given interval, than smaller particles, with same volume of suspension injected into a porous medium when steric hindrance is unimportant. This is consistent with the data on tortuosity and suggests that larger hydrodynamic forces propel the larger particles. The values of actual average speeds, VLa, for the smaller particles are higher than for the large particle because the smaller particles travelled longer distances in the circuit of the micro model.

The third parameter is the translational dispersion coefficient. Dispersion (or spreading) of particles in the suspension will occur as a result of a combination of different effects. At any cross-section of the micro model, the velocity of the fluid is non-uniform and Taylor dispersion occurs [33]. The channel is tortuous and particles travel at different average speeds along different paths that depend on where each particle happens to be initially located. Particles experience lateral displacements due to lift induced by rotation or collisions (the chromatographic effect), and particles are subject to thermal fluctuations that change their directions of motion on short time scales (Brownian motion).

At the macroscopic scale, micro-models are treated as 1-dimensional, homogeneous domains but they are not isotropic. For a net bulk flow of a suspension along direction x and a suspension with a solid population density C, the material balance equation at steady state is:

Where Vx is an average velocity derivable from Darcy's law, and KL is the coefficient of longitudinal dispersion. The coefficient is estimated from [11, 32]

where Lai is the actual distance travelled by a particle from its initial position 4 cycles earlier (a cycle is the space between alternate rows of posts or grids, i.e. 10 consecutive pores), and La Av are the average distances for N particles in a set, and ti is the time elapsed for each particle. The result presented in Table 4 shows that dispersion increases with the flow rate of the suspension for all particles sizes, is larger for the smaller particles and increases with the solid density of the micro model configuration.

The relative contributions of hydrodynamic factors (advection) and thermal fluctuations to dispersion can be explored by reference to a dimensionless quantity, the Peclet number, Pe (ul/Di) where u is a characteristic fluid velocity, l is a length scale and Di is the coefficient of diffusion. For this study, u is the average pore velocity, l is the diameter of the post (corresponding to grain size in a particulate bed) and Di is the diffusion coefficient for particles in suspension. The present case corresponds to the situation for dilute suspensions in which particles denser than the fluid are isolated [29,34,35].The translational diffusion coefficient for a sphere is given by the Stokes- Einstein equation [34]

where k is the Boltzman constant, T is absolute temperature, μ is the dynamic viscosity of the fluid and a is the radius of the sphere. At 20°C, estimates for Di (1012) are 2.15, 0.86 and 0.286m2/s for the 200, 500 and 1500 nm diameter particles respectively.

Experimentally derived dispersion coefficient divided by the diffusion coefficients are plotted versus Peclet number, Pe, for all the experimental conditions in (Figure 11). As per previous studies, the data indicate that the dispersion of the suspended particles is controlled by advection rather than by diffusion for Pe> 10.

Conclusion

The transport of ultrafine and colloidal particles in dilute suspensions through micro models of porous media has been studied experimentally under conditions that hydrodynamic factors dominate. Particle trajectories were not coincident with streamlines for the continuous phase, and particles show evidence of Brownian motion and drifts due to local velocity gradients in the suspending medium. The particles showed significant changes in speed as they traversed the media and the "slip condition" between particle and fluid seems to prevail for most of the domain. Larger particles travelled faster and further linearly into the porous medium than the smaller particles. Smaller particles, in turn, spread out axially more than the larger particles as they are carried through the medium. Dispersion was higher in the less porous structures.

Acknowledgement

The authors are grateful for support from the University of Calgary and the Advanced Energy Consortium (AEC) at the Bureau of Economic Geology (UT-Austin).

References

  1. Heyder J, Gebhar J, Rudolf G, Schiller CF, Stahlhofen W. Deposition of particles in the human respiratory tract in the size range 0.005-15 micrometer. J Aerosol Science. 1986; 17: 811.
  2. Zheng C, Bennett GD. Applied Contaminant Transport Modeling: Theory and Practice. NewYork: Van Nostrand Reinhold. 1995; 464.
  3. Javadpour F, Amrein M, Jeje A. Multiscale Experimental Study of Selective Blood-Cell Filtration in Fibrous Porous Media. J Transport in Porous Media. 2012; 91: 913-926.
  4. Lee J, Koplik J. Microscopic motion of particles flowing through a porous medium. J Physics of Fluids. 1999; 1176-1187.
  5. Karadimitriou NK, Hassnizadeh SM. A review of micromodels and their use in two-phase flow studies. J Vadose Zone. 2011.
  6. Wilson J, Conrad S, Hagan E, Mason W, Peplinski W. The pore level spatial distribution and saturation of organic liquids in porous media, National Water Well Association. Dublin. 1988; 107-133.
  7. Shapiro M, Kettner I, Brenner H. Transport Mechanics and collection of sub micrometer particles in fibrous filters. J Aerosol Sci. 1991; 22: 707-722.
  8. Brown RC. Theory of airflow through filters modelled as arrays of parallel fibers. Chem. Engg. Sci. 1993; 48: 3535-3543.
  9. Hellou M, Martinez JE, Yazidi M. Stokes flow through microstructural model of fibrous media. Mechanics Research Communications. 2004; 31: 97-103.
  10. Di Carlo D, Irimia D, Tompkins RG, Toner M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc Natl Acad Sci U S A. 2007; 104: 18892-18897.
  11. Auset M, Keller A. Pore-scale processes that control dispersion of colloids in saturated porous media. J Water Resources Res. 2004; 40: 1-11.
  12. Javadpour F, Jeje A. Modeling Filtration of Platelet-Rich Plasma in Fibrous Filters. J Transport in Porous Media. 2012; 91: 677-696.
  13. Kirsch AA, Fuchs NA. The fluid flow in a system of parallel cylinders perpendicular to the flow direction at small Reynolds numbers. J. Phys. Soc. Jpn. 1967; 22: 1251-1255.
  14. Baumann T, Toops L, Niessner R. Colloid dispersion on the pore scale. Water Res. 2010; 44: 1246-1254.
  15. Dryden HL, Murnaghan FD, Bateman H. Hydrodynamics Bull. 1932; 84: 197.
  16. Hartnett JP, Kostic M. Heat Transfer to Newtonian and Non-Newtonian Fluids in Rectangular ducts. Adv. In Heat Transfer. 1989; 19: 247-356.
  17. Qu W, Mudawar I. Analysis of three-dimensional heat transfers in micro-channel heat sinks. Int. J Heat and Mass Transfer. 2002; 45: 3973-3985.
  18. Sajjadiani S. Transport of ultra-fine particles in suspension through structured micro-models. MSc thesis, University of Calgary. 2014.
  19. Falade A, Brenner H. First-Order wall curvature effects upon the Stokes resistance of a spherical particle moving in close proximity to solid wall. J Fluid Mech. 1988; 193: 533-568.
  20. Happel J. Viscous flow relative to arrays of cylinders. A.I.Ch.E. J. 1959; 5: 174-177.
  21. Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. J. Phys. Soc. Jpn.1959; 14: 527-532.
  22. Gordon D. Numerical Calculations on viscous flow fields through cylinder arrays. J Computers and Fluids. 1978; 6: 1-13.
  23. Sangani AS, Acrivos A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiphase Flow. 1982; 8: 193-206.
  24. Drummond JE, Tahir MI. Laminar viscous flow through regular arrays of parallel solid cylinders. Int. J. Multiphase Flow. 1984; 10: 515-540.
  25. Ingham DB, Hildyard ML, Heggs PJ. The particle collection of an array of cylinders using the boundary element method. Engg Analysis with Boundary Elements. 1991; 8: 36-44.
  26. Wang CY. Stokes slip flow through square and triangular arrays of circular cylinders, Fluid Dynamics Research. 2003; 32, 233-246.
  27. Hellou M, Martinez JE, Yazidi M. Stokes flow through microstructural model of fibrous media. J Mechanics Research Communications. 2004; 31: 97-103.
  28. Chandrasekhar S. Stochastic Problems in Physics and Astronomy. J Rev. Mod. Phys. 1943; 15: 1-89.
  29. Probstein RF. Physicochemical Hydrodynamics and introduction. Boston: Butterworth. 1989; 114-121.
  30. Mazo RM. Brownian motion Fluctuations, Dynamics and Applications. Oxford: Clarendon Press. 2002.
  31. Chandrasekhar S. Brownian motion, Dynamical Friction and Stellar Dynamics. Rev. Mod. Phys. 1949; 21: 383-388.
  32. Fetter CW. Contaminant Hydrogeology. New York: Macmillan Publ. Co.1993.
  33. Taylor GI. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. Roy. Soc. 1953; A219, 186-203.
  34. Einstein A. Investigation on the Theory of the Brownian Movement Edited with notes by R. Furth. New York: Dover. 1956.
  35. Lebowitz JL, Rubin E. Dynamical Study of Brownian Motion. J Phys. Rev. 1963; 131: 2381-2396.

Citation: Sajjadiani S, Javadpour F and Jeje AA. Trajectory and Transit Patterns of Isolated Nanoparticles in Structured Micromodels. Austin J Chem Eng. 2014;1(2): 1006. ISSN 2381-8905