
Review Article
Austin Chem Eng. 2019; 6(1): 1065.
Effects of Cross Diffusion and Radiation on Magneto Mixed Convective Stagnation Flow from a Vertical Surface in Porous Media with Gyrotactic Microorganisms
Nima NI1,2, Ferdows M2,3*, Ardekani MM4 and Alzahrani F3
1Department of Applied Mathematics, University of Dhaka, Bangladesh
2Department of Quantitative Sciences, International University of Business Agriculture and Technology, Dhaka, Bangladesh
3Department of Mathematics, Faculty of Science, King Abdulaziz University, Saudi Arabia
4Department of Mechanical and Aeronautical Engineering, University of Pretoria, Pretoria, South Africa
*Corresponding author: Mohammad Ferdows, Department of Applied Mathematics, University of Dhaka, Bangladesh
Received: March 07, 2019; Accepted: April 16, 2019; Published: April 23, 2019
Abstract
In this paper the Soret and Dufour effects on steady mixed convective boundary layer flow on a vertical surface embedded in porous medium subjected to a magnetic field containing gyrotactic microorganism is studied. The governing momentum, energy, concentration and microorganism equations are transformed into a set of coupled differential equations. The obtaining equations are solved by MAPLE 14.0 algorithm and the numerical result for different values of Soret number Sr, Dufour number Df, Lewis number Le, bioconvection Lewis number Lb, bioconvection peclet number Pb, Hartmann number Ha2, thermal radiation parameter Rd and buoyancy numbers is presented graphically for both assisting and opposing flow. Comparisons are made with available published results as special cases to validate numerical data and excellent compatibility is found. The effects of physical parameters on nusselt number, Sherwood number and density of motile microorganism are also presented. It is observed that diffusion thermo and thermal diffusion effects on temperature, concentration and microorganisms profile distributions are quite opposite.
Keywords: Boundary Layer Flow; Double Diffusive; Sacling Analysis; Nonliner ODE; Flow Solutions; Physical Parameters.
Subject Classification: 76Dxx
Introduction
The mixed convection (combined free and forced) boundary layer flow has attracted considerable attention in recent years because of their wide applications in nuclear reactor technology transpiration cooling, separation process in aquifer, ground water pollution, oil recovery processes, food processing, drawing of plastic films, hot rolling and continuous casting of metals and spinning of fibers, glass-fiber and paper productions. Sakiadis [1,2] studied the boundary layer flow through a moving surface. Grubka and Bobba [3], Elbashbeshy [4] observed temperature field in the boundary layer flow over a stretching surface. Cheng [5] studied the mixed convection flow on inclined surfaces in a porous medium. The mixed convection along a nonisothermal wedge in a porous medium was studied by Kumari and Gorla [6]. The Neild and Bejan [7], Ingham and Pop [8,9] , Vafai [10] have reported the detailed review of the convection through porous media. Now a days the large number of publications, Lai [11], Postelnicu [12], Chamka and Khaled [13],Bansod and Ambedkar [14], Srinivasachary and Surender [15], Garg [16], Swamy [17], of the mixed convective heat and mass transfer in porous media have been studied for vertical surfaces.
The study of microorganism is called microbiology. Great attentions are paid to biological fluid mechanism particular in the field of microbiology where developments of microorganisms (e.g. motile species of bacteria and algae) in bioconvection are studied. It is commonly observed that in fluid mechanics solid particles are either carried by the fluid flow or pushed by external forces. Bio-convection patterns are inspected in cultures of swimming micro-organisms which are heavier than water and tend to propel themselves toward the upper surface of their environment in response to external stimuli such as gravity, light, and chemical gradient. Bioconvection can also be classified as the macroscopic fluid motion because of the density gradient associated with swimming micro-organisms [18–22] which intensify the density of base fluid in a specific direction that causes bioconvection flow.
Scientists formulate models to observe the fluid motions associated with aquatic microorganisms. A large number of mechanisms are developed that force microorganisms to swim in specific directions depending on the ambient condition. There are different types of motile micro-organisms such as oxytactic or chemotaxis, negative gravitaxis and gyrotactic micro-organisms according to their impelling behavior. Neild and Bejan [7] defined bioconvection as “Pattern formation in suspensions of microorganisms such as bacteria and algae due to up swimming of the microorganisms”. Gyrotactic microorganisms such as Cnivalis swim upward in still water due to the fact that their center of mass is located behind their center of buoyancy. The behavior of mixed convection in suspensions of gyrotactic/oxytactic microorganisms is discussed widely in [23-27].
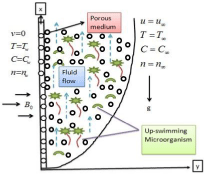
Figure 1: Physical Model.
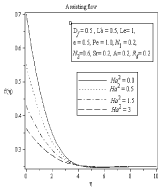
Figure 2a: Effect of Hartmann Number Ha2 on velocity profile n.
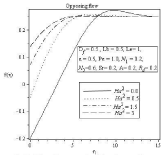
Figure 2B: Effect of Hartmann Number Ha2 on velocity profile.
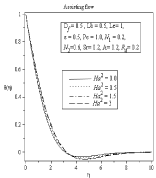
Figure 3A: Effect of Hartmann Number Ha2 on temperature profile.
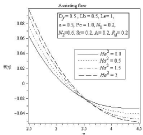
Figure 3B: Effect of Hartmann Number Ha2 on temperature profile.
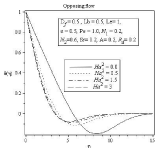
Figure 3C: Effect of Hartmann Number Ha2 on temperature profile.
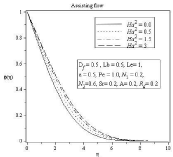
Figure 4A: Effect of Hartmann Number Ha2 on concentration profile.
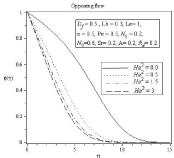
Figure 4B: Effect of Hartmann Number Ha2 on concentration profile.
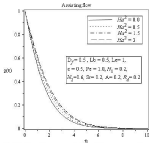
Figure 5A: Effect of Hartmann Number Ha2 on microorganism profile.
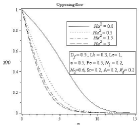
Figure 5B: Effect of Hartmann Number Ha2 on microorganism profile.
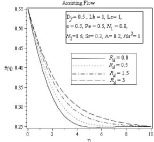
Figure 6A: Effect of Radiation parameter Rd velocity profile.
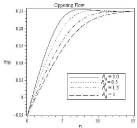
Figure 6B: Effect of Radiation parameter Rd velocity profile.
Nowadays analyzing Soret and Dufour effects on convective processes have sprung researchers’ interests. Thermal diffusion or Soret effect is a mass flux due to temperature gradient [28]. The higher the temperature gradient, the larger the Soret effect is. Dufour effect is enthalpy flux due to concentration gradient. As observed in a moving fluid, energy flux can be generated by both temperature and concentration gradient which causes the Dufour (thermo-diffusion) and the Soret (thermal-diffusion) effects. Since in most cases, Dufour and Soret effects are in smaller order of magnitudes than thermo-fluid effects described by Fourier’s and Fick’s laws, they are neglected in many studies. However, Ecket and Drake [29], Mortimer and Eyring [30] describe several cases where diffusion-thermo and thermal-diffusion effects are quite significant. Cheng [31], Srinivasacharya [32] presented Soret and Dufour effects on mixed convection heat and mass transfer in porous medium. El –Aziz [33] studied effects of Soret and Dufour parameters on velocity, concentration and temperature profiles. Mohammed Ahmed [34] showed the effects of cross-diffusion and radiation on mixed convection from a vertical plate in a fluid saturated porous medium.
The study of magnetic field has been a focused in recent researches due to its wide applications in many engineering fields such as in petroleum engineering, chemical engineering, composite or ceramic engineering, biochemical engineering and heat exchangers. The applications of magnetic field to convection processes also constitute a major field of interest (Magneto-Hydrodynamic or MHD) in many areas of engineering and physical sciences such as crystal growth, metal casting and liquid metal cooling blankets for fusion reactors. The effect of a magnetic field on convective fluid flow in porous media has been investigated in the following studies, Postelnicu [35] investigated on influence of magnetic field on natural convection considering Soret and Dufour effects. Zhang e [36] investigated MHD radiative flow of nanofluid over a surface with variable surface heat flux and chemical reaction. Khan [37] analyzed non-aligned MHD radiative flow of variable viscosity nanofluid past a stretching surface. Effect of inclined magnetic field in third grade fluid flow with variable thermal conductivity is presented by Hayat [38]. Alsaedi [39] studied MHD bioconvective flow in the presence of nanofluid containing microorganism.
Our aim in this paper is to analyze a steady mixed convective flow containing gyrotactic microorganisms over a vertical plate in porous medium coexistence diffusion thermo, thermal diffusion effects in the presence of external magnetic field. The behavior of entire boundary layer thickness of velocity, temperature, concentration and microorganism profile is observed for different values of bioconvection parameters. The effect of Nusselt number, Sherwood number as well as density of motile microorganism on increasing value of bioconvection parameters, Soret and Dufour number, Hartmann number, radiation parameter are investigated in this study. The impact on different profile distributions are analyzed separately for natural, forced and also mixed convection regimes.
Mathematical Formulation
Consider the problem of two-dimensional steady-state boundary layer flow of hydromegnetic fluid containing gyrotactic microorganisms. Due to gravity the fluid and microorganisms both fall downwards along a vertical flat plate. The coordinate system was chosen such that x-axis is along the plate and y-axis is normal to it. The schematic sketch of the problem is shown in Figure 1. The vertical wall is kept at constant distributions such as temperature Tw, the fluid volume fraction Cw and the density of motile microorganisms nw .which are considered to be greater than the ambient temperature and concentrationsT∞, C∞ and n∞.
The governing partial differential equations related to conservation of mass, momentum, energy, oxygen and microorganisms using the Oberbeck-Boussinesq approximation can be written as,
In equation (2), plus (+) sign indicates assisting flow and minus (-) sign indicates opposing flow. Using Rosseland approximation (Raptis [40] and Sparrow [41]) radiative heat flux term can be defined as,
Where and are the Stefan-Boltzman constant and the mean absorption co-efficient.
Introducing following dimensionless quantities
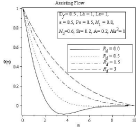
Figure 7A: Effect of Radiation parameter Rd on temperature profile.
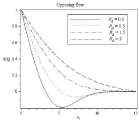
Figure 7B: Effect of Radiation parameter Rd on temperature profile.
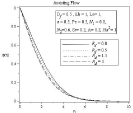
Figure 8A: Effect of Radiation parameter Rd on concentration profile.
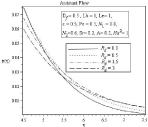
Figure 8B: Effect of Radiation parameter Rd on concentration profile.
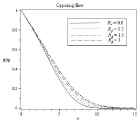
Figure 8C: Effect of Radiation parameter Rd on concentration profile.
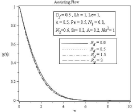
Figure 9A: Effect of Radiation parameter Rd on microorganism profile.
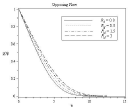
Figure 9B: Effect of Radiation parameter Rd on microorganism profile.
It's noteworthy that ε=0 (Pex=0) and ε=1 (Rax=0) respectively corresponds to pure free convection, pure forced convection. So any value between ε=0 to ε=1 corresponds to mixed convection regime.
The quantities of practical interest in this study are the local Nusselt number Nux, the Sherwood number Shx) and the local density number of the motile microorganisms Nnx are defined as
Where qw , qm, and qn are the wall heat, the wall mass and wall motile microorganisms fluxes, respectively and are defined as
Numerical solution
The governing partial differential equations (1-7) were transformed into ordinary differential equations (11-16) respectively using similarity solutions and then numerically solved by using Maple 14.0 with the help of dsolve command. The type of BVP or IVP problems were identified and appropriate algorithms were implemented. The reliability and accuracy of Maple’s algorithm have been repeatedly verified in several recent research papers. For the further confirmation present results for the special cases are compared with some published results investigated by Hseieh [40],Ching-Yang Cheng[41], Gorla [42], A.J.Chamka [43].The asymptotic boundary conditions given by equation (15-16) were replaced by using a value of 15 for the similarity variable ηmax as follows: ηmax=15,f' (15)=0,θ(15)=0,φ(15)=0,σ(15)=0.
Result and Discussion
In figure (2-5) Effect of Hartmann number on velocity, temperature, concentration and microorganism profile is observed for Df=0.5,Lb=0.5,Le=1,ε=0.5,Pe=1.0,N1=0.2,N2=0.6,Sr=0.2,A=0.2,Rd=0.2. The behavior of different profiles in all case is observed for assisting and also opposing flow. It is well known that the influence of magnetic field can be represented by Hartmann number. The Lorentz force rises if transverse magnetic field is placed normal to the flow direction. This resistive –type force declines the motion of the fluid flow and increases the temperature of flow. As a result boundary layer thickness of concentration and microorganism profile increases with the increasing value of Hartmann number. In Figure 3(b) we can see thermal boundary layer thickness increases in the similar way according to increasing value of Hartmann number but after point η=3.513 thermal boundary layer decreases. For all profiles opposite effects are observed for opposing Flow.
In Figure (6-9) effect of radiation parameter is observed Df=0.5, Lb=1, Le=1, ε=0.5, Pe=0.5, N1=0.8, N2=0.6, Sr=0.2, A=0.2, Ha2=1. In 6(a) the velocity profile and corresponding boundary layer thickness increases with the increasing of radiation parameter Rd. As higher values of radiation parameter implies higher surface heat flux, in Figure 7(a-b) it is observed that thermal boundary layer thickness greatly increases for assisting flow and also for opposing flow. When radiation parameter is negligible temperature profile decreases, but after η ≈ 3.611 it increases for assisting flow. The concentration and microorganism profile decreases with the increases of radiation parameter in Figure 8(a) to 9(b).
Effect of different values of mixed convection parameter is observed for the values Df=0.5, Lb=1, Le=1, Rd=0.5, Pe=0.5, N1=0.8, N2=0.6, Sr=0.2, A=0.2, Ha2=1 in figure (10-13). With the increasing of mixed convection parameter velocity profile increases. So momentum boundary layer thickness gradually increases from free convection to forced convection regime. For the influence of mixed convection parameter number of stagnation point flow observed for temperature profile 11(a). It can be seen clearly on 11(b). For ε=0.7,ε=1 temperature, concentration and also microorganism profile remains almost similar to assisting flow in case of opposing flow but for ε=0,ε=0.3 the characteristic of temperature, concentration and microorganism profile is quite opposite. In 12(a) and 13(a) it is observed that concentration and microorganism profile decreases with higher values of mixed convection parameter.
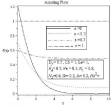
Figure 10A: Effect of mixed convection parameter on velocity profile.
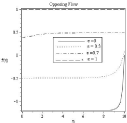
Figure 10B: Effect of mixed convection parameter on velocity profile.
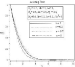
Figure 11A: Effect of mixed convection parameter on temperature profile.
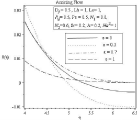
Figure 11B: Effect of mixed convection parameter on temperature profile.
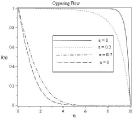
Figure 11C: Effect of mixed convection parameter on temperature profile.
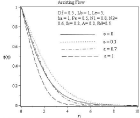
Figure 12A: Effect of mixed convection parameter on concentration profile.
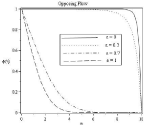
Figure 12B: Effect of mixed convection parameter on concentration profile.
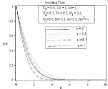
Figure 13A: Effect of mixed convection parameter on concentration profile.
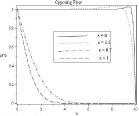
Figure 13B: Effect of mixed convection parameter on concentration profile.
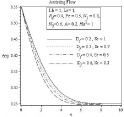
Figure 14A: Effect of soret and dufour number on velocity profile.
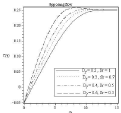
Figure 14B: Effect of soret and dufour number on velocity profile.
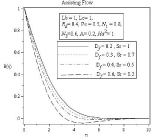
Figure 15A: Effect of soret and dufour number on Temperature profile.
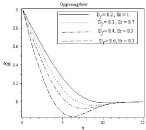
Figure 15B: Effect of soret and dufour number on Temperature profile.
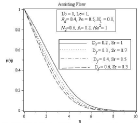
Figure 16A: Effect of soret and dufour number on concentration profile.
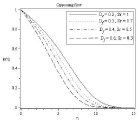
Figure 16B: Effect of soret and dufour number on concentration profile.
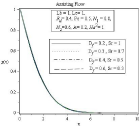
Figure 17A: Effect of soret and dufour number on microorganism profile.
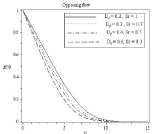
Figure 17B: Effect of soret and dufour number on microorganism profile.
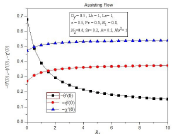
Figure 18A: variation of nusselt number, Sherwood number and density of
motile microorganism for different values of radiation parameter.
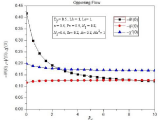
Figure 18B: variation of nusselt number, Sherwood number and density of
motile microorganism for different values of radiation parameter.
In figure 14(a) to 17(b) it is observed that all the profile distributions are decreasing with the increasing of Dufour number and decreasing of Soret number. So it can be stated that Soret and dufour effects on velocity, temperature, concentration and microorganism profile are quite opposite. Here another noticeable thing is except velocity profile figure 14(b) in all figure: 15(b), 16(b), 17(b) boundary layer thickness are decreasing for opposing flow similar to assisting flow.
Effect of Hartmann number Ha2 on nusselt number -θ'(0), Sherwood number (-φ)' (0), density of motile microorganism -χ' (0) is observed in Table 1. With the increasing of Hartmann number nusselt number, Sherwood number and density of motile microorganism decrease for assisting flow and decrease for opposing flow. In Table 2 nusselt number -θ'(0), Sherwood number -φ'(0), density of motile microorganism -χ'(0) increases for assisting flow with the increasing of dufour number and decreasing of Soret number. Opposite behavior is observed for opposing flow. Effect of radiation parameter is shown graphically in Figure 18(a) and 18(b). In 18(a) nusselt number decreasing, Sherwood number and density of motile microorganism increasing. Similar effect is observed for nusselt number in 18(b) for opposing Flow. Some of our obtaining result has been compared with some published results which are presented in Table 3 and Table 4.
Conclusion
In this study we have considered mixed convective flow over a vertical plate in porous media with Gyrotactic microorganisms to analyze the effect of cross diffusion, thermal radiation on velocity, Temperature, concentration and microorganism profile. The results obtained from our analysis are as follows:
For assisting flow with the increasing of Ha2, Df and decreasing of sr velocity profile decreases, on the other hand velocity profile increases with the increasing of Rd and mixed convection parameter ε.
For both assisting and opposing flow stagnation flow is observed for temperature profile. It increases with the increasing of Ha2, Df and also ε. In case of opposing flow for temperature profile remains unchanged in forced convection regime. For Rd temperature profile decreases.
Concentration profile increases with Ha2 and sr, decreases with the increasing values of Df. Stagnation flow is observed for Rd and ε. For opposing flow concentration profile has no effect in forced convection regime.
For assisting flow microorganism profile increases with Ha2 and Rd. Soret and Dufour number have very negligible effect on microorganism profile.
References
- Sakiadis BC. Boundary layer behavior on continuous solid surfaces, I: boundary layer equations for two dimensional and axi-symmetric flow. AIChE Journal. 1961; 7: 26-28.
- Sakiadis BC. Boundary layer behavior on continuous solid surfaces, II: boundary layer on a continuous flat surfaces. AIChE Journal.1976; 7: 221-225.
- Grubka IJ, Bobba KM. Heat transfer characteristic of a continous stretching surface with variable temperature, Journal of Heat Transfer. 1985; 107: 248-250.
- Elbashebeshy MA. Heat transfer over a stretching surface with variable surface heat flux. Journal of Physics D: Applied Physics. 1998; 31: 1951-1654.
- Cheng P: Combined free and forced convection flow about inclined surfaces in porous media. International Journal of Heat and mass transfer. 1977; 20: 807-814.
- Kumari M, Gorla RSR: Combined convection along a non-isothermal wedge in a porous medium. Heat Mass Transfer. 1997; 32: 393-398.
- Neild DA, Bejan A. Convection in Porous Media, Springer. New York, 1992.
- Ingham DB, Pop I. Transfer phenomena in Porous Media I, Pergamon, Oxford. 1998.
- Ingham DB, Pop I. Transfer phenomena in Porous Media II, Pergamon, Oxford. 2002.
- Vafai K, Handbook of Porous Media. Begell House. New York, 2000.
- Lai FC, Coupled heat and mass transfer by mixed convection from a vertical plate in a saturated porous medium International communications in Heat and mass transfer. 1991; 18: 83-106.
- Postelnicu A. Influence of Chemical reaction on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Doufour effects, International Journal of Heat and mass transfer. 2007; 43: 595-602.
- Chamka AJ, Khaled AR. Non-similar hydro-magnetic simultaneous heat and mass transfer by mixed convection from a vertical plate embedded in a uniform porous medium. Numerical Heat Transfer. 1999; 36: 327-344.
- Bansod VJ, Ambedkar B. An integral treatment for combined heat and mass transfer by mixed convection along vertical surface in a saturated porous medium, Journal of Mechanical Engineering Research. 2011; 3: 138-151.
- Srinivasachary D, Surender O. Effect of double stratification on mixed convection boundary layer flow of a nano fluid past a vertical plate in a porous medium. Applied Nanoscience. 2015; 5: 29-38.
- Garg P, Purohit GN, Chaudhary RC. Similarity Solution for Combined Free-Forced Convection Past a Vertical Porous Plate in a Porous Medium with a Convective Surface Boundary Condition, International Journal of Applied Mechanics and Engineering. 2016; 21: 827-836.
- Srinivasachary D, SwamyReddy G. Mixed convection on a vertical plate in a power law fluid saturated porous medium with cross diffusion effects, Procedia engineering. 2015; 127: 591-597.
- Kuznetsov AV. The onset of thermo-bioconvection in a shallow fluid saturated porous layer heated from below in a suspension of oxytactic micro-organisms, European Journal of Mechanics –B/Fluids. 2006; 25: 223-233.
- Hill NA, Pedley TJ. Bioconvection. Fluid Dynamic Research. 2005; 37: 1-20.
- Avramenko AA, Kuznetsov AV. Stability of a suspension of gyrotactic micro-organisms in superimposed fluid and porous layers. International Communications in Heat and mass transfer. 2004; 31: 1057-1066.
- Avramenko AA, Kuznetsov AV. The onset of bio-thermal convection in a suspension of gyrotactic micro-organisms in a fluid layer with an inclined temperature gradient. International Journal of Numerical methods for Heat & Fluid flow. 2010; 20: 111-129.
- Alloui Z, Nguyen TH, Bilgen E. Numerical investigation of thermo-bioconvection in a suspension of gravitactic micro-organisms. International Journal of Heat and Mass Transfer. 2007; 56: 1435-1441.
- Uddin MJ, Khan WA and Ismail AIM. J.Thermophys.Heat Transf. 2013; 27: 326-333.
- Uddin MJ,Khan WA and Ismail AIM. J.Nanoeng.Nanosys. 2013; 227: 11-18.
- Kuznetsov AV.”The onset of nanofluidbioconvection in a suspension containing both nano particles and gyrotacticmicroorganisms,”International communications in Heat and mass transfer. 2010; 37: 1421-1425.
- Khan WA, Makinde OD. MHD nanofluid bioconvection due to gyrotactic microorganisms over a convectively heat strechingsheet,International Journal of Thermal Sciences. 2014; 81: 118-124.
- Raees A, Hang Xu, Sun Q. Mixed convection in gravity -driven nanoliquid film containing both nanoparticles and gyrotactic microorganism. Applied Mathematics and Mechanics. 2015.
- Soret C. Influence de la temperature sur la distribution des sels dans leurs solutions, C R Acad Sci Paris. 1880; 91: 289-291.
- Eckert ERG, Drake RM. Analysis of Heat and Mass Transfer. McGraw-Hill, New York. 1972.
- Mortimer RG, Eyring H. Elementary transition state theory of the Soret and Dufour effects, Proceedings of the National Academy of Sciences. 1980; 77: 1728-1731.
- Cheng-Yang Cheng. Soret and Dufour effects on Mixed Convection Heat and Mass Transfer from a vertical wedge in a porous medium with constant wall temperature and concentration. Springer. 2012; 94: 123-132.
- Srinivasacharya D, Mallikarjuna B, Bhuvanavijaya R. Soret and Dufour effects on mixed convection along a vertical wavy surface in a porous medium with variable properties. Ain Shams Engineering Journal. 2015; 6: 553-564.
- M.A.El-Aziz. Thermal diffusion and diffusion-thermo effects on combined heat mass transfer by hydromagnetic three-dimensional free convection over a permeable stretching surface with radiation. Physics Letter A. 2008; 372: 263-272.
- Ahmed MM, Mohammed ME, Khidir AA. The effects of cross-diffusion and radiation on mixed convection from a vertical flat plate embedded in a fluid- saturated porous medium in the presence of viscous dissipation, Population and Power Research. 2016.
- Postelnicu A. Influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effect, International Journal of Heat and Mass Transfer. 2004; 47: 1467-1472.
- Zhang C, Zheng L, Zhang X, Chen G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction, Applied Mathematical Modeling. 2015; 39: 165-181.
- Khan WA, Makinde OD, Khan ZH. Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat, International Journal of Heat Mass Transfer. 2016; 96: 525-534.
- Hayat T, Shafiq A, Alsaedi A, Asghar S. Effect of inclined magnetic field in flow of third grade fluid with variable thermal conductivity, AIP Advances. 2015; 5: 087108.
- Alsaedi A, Khan MI, Farooq M, Gull N, Hayat T. Magnetohydrodynamic (MHD) stratified bioconvective flow of nanofluid due to gyrotactic microorganisms, Advanced Powder Technology. 2017; 28: 288-298.
- Raptis A. Radiation and free convection flow through a porous medium. International communication in Heat and Mass Transfer. 1998; 25: 289-295.
- Sparrow EM, Cess RD. Radiation Heat Transfer. Hemisphere. Washington. 1978.
- Hsieh JC, ChenTS, Armaly BF. Mixed convection long a non-isothermal vertical plate embedded in a porous medium: the entire regime, International Journal of Heat Mass Transfer. 1993; 36: 1819-1825.
- Cheng CY. Soret and Dufour effects on Mixed Convection Heat and Mass Transfer from a Vertical Wedge in a porous medium with constant wall temperature and Concentration. Transport in porous media. 2012; 94: 123-132.
- Gola RS, Bakir AY, Byrd L. Effects of thermal dispertion and stratification on combined convection on a vertical surface embedded in a porous medium. Transport in porous media. 1996; 25: 275-282.
- Chamka AJ, Khaled ARA. Hydro magnetic simultaneous heat and mass transfer by mixed convection a vertical plate embedded in a stratified porous medium with thermal dispersion effects. Heat and mass transfer. 2000; 36: 63-70.