
Research Article
Austin J Clin Cardiolog. 2022; 8(3): 1099.
Diastolic Blood Pressure Determinants for Prostate Cancer Patients
Das M1, Gong R2, Sahoo RK3, Devi RS4, Banik S5 and Das RN6*
1Department of History, The University of Burdwan, Burdwan, West Bengal, India
2Department of Informatics and Mathematics, Mercer University, Macon, GA, USA
3Shool of Statistics, G. M. University, Sambalpur, Odisha, India
4Department of Statistics, Moreh College, Moreh, Manipur, India
5Department of Physical Sciences, Independent University, Bangladesh, Dhaka, Bangladesh
6Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
*Corresponding author: Rabindra Nath Das, Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
Received: October 20, 2022; Accepted: November 19, 2022; Published: November 26, 2022
Abstract
The association between the hypertension risk factors such as diastolic and systolic blood pressure with the Prostate Cancer (PC) risk factors is controversial. The report derives the determinants of the Diastolic Blood Pressure (DBP) of the PC patients. It is derived herein that mean DBP is directly associated with serum Haemoglobin (HG) (P=0.017), and Systolic Blood Pressure (SBP) (P<0.001), while it is negatively associated with the subject’s age (P<0.001). Variance of DBP is higher for normal subjects (P=0.004) than PC patients. Variance of DBP is higher for Cardiovascular Disease (CVD) history (P=0.060) subjects than normal, PC patients with Bone Metastases (BM) (P=0.002) than normal, and heart patients identified by Electrocardiogram (EKG) (P=0.046) than normal and benign. These associations of DBP for PC patients are derived based on the statistical Joint Generalized Linear Models (JGLMs) method. It is concluded herein that mean DBP is independent of PC risk factors, while it is observed that DBP is highly scattered for PC patients with BM. For PC patients with hypertension, care should be taken on DBP, SBP and HG only.
Keywords: Bone metastases (BM); Diastolic blood pressure (DBP); Prostatic acid phosphatase (PAP); Prostate cancer (PC); Systolic blood pressure (SBP); Non-constant variance
Introduction
Hypertension and PC are commonly critical conditions among senior men throughout the world [1]. Generally, PC is the most common cancer in senior men, and most of them are suffering from hypertension [2-5]. Consequently, SBP and DBP are at higher levels for these hypertension PC patients [6-11]. The universal agestandardized prevalence of elevated hypertension risk factor, namely blood pressure (BP) (SBP ≥140 mmHg or DBP ≥90 mmHg) in men was estimated as ≥20% in 2015 [12].
It is well known for several decades that the elevated BP is a sign for development of any disease, which reflects a long cumulative exposure in ageing-related diseases such as PC and diabetes [13]. Note that hypertension is associated with inflammation that is a hallmark of cancer development [5,14]. The inflammatory cells in the prostate microenvironment linked to precursor lesions for PC in the prostate gland, known as proliferative inflammatory atrophy, have been found [13,14]. It was observed that systemic prediagnostic inflammatory biomarkers including high sensitive C-reactive protein and white blood cells were linked to PC development [6,13,14].
The earlier reported linkages between hypertension and PC risk factors was controversial [2,8]. The present article aims to derive the explanatory factors (or determinants) of DBP for PC patients using an appropriate probabilistic model. In the PC literature, the relationship of DBP with PC biomarkers or risk factors is not clear. In addition, most of the earlier articles tried to derive the association of DBP for PC patients based on percentage, meta-analysis, correlation, confidence intervals etc, which are not appropriate [1,2,8,10-12,15- 18]. The article investigates the following hypertension PC research queries.
• Is DBP associated with PC biomarkers? What are the determinants of DBP for PC patients? This is the principal hypertension query in PC epidemiology.
• How can one obtain the determinants of DBP?
• What are the effects of DBP on PC patients?
The article examines these above queries adopting the sections materials & methods, statistical analysis, results & discussions, and conclusions. The identified DBP determinants are presented in (Table 1), while the explanatory factors are derived by joint generalized linear models (JGLMs), and the effects of DBP are focused in the discussion section.
Materials and Methods
Materials
The present study considers a data set on a randomized clinical trial performed on 474 PC subjects with third or fourth stage PC. The contributor of the data set was D.P. Byar, who published a few analyses of the data set along with his coauthors [19,20]. The data set was well described in the book by Andrews and Herzberg [21]. For every subject, the following factors were noted: 1. Study unit’s stage (=S-stage=F1) (0= no cancer; 1= PC); 2. Estrogen (mg) (=RX=z2); 3. Months of follow up (=D-time=z3); 4. Survival status (Alive=F4) (0=Alive; 1= Dead due to PC; 2= Dead due to heart or vascular; or cerebrovascular; or pulmonary embolism; or other cancer; or respiratory disease; or other specific non-cancer; or unspecified non-cancer; or unknown cause); 5. Age(=z5); 6. Weight (= Wt= z6); 7. Performance Rating (=PFR=F7) (0= normal activity; 1= confined to bed; 2= in bed < 50% daytime; or in bed >50% daytime); 8. Cardiovascular Disease History (=CVDH=F8) (0=no, 1=yes); 9. Systolic Blood Pressure (=SBP=x9); 10. Diastolic Blood Pressure (=DBP=z10); 11. Electrocardiogram Code (= EKG=(F11) (0=normal; 1=benign; 2= rhythmic disturb & electrolyte; or heart block; or conduction; or heart strain; or old Myocardial Infarction (MI); or recent MI); 12. Serum Haemoglobin (=HG=z12); 13. Size of primary tumour (SZ=z13); 14. Index of tumour stage and histolic grade (= SG= z14); 15. Serum prostatic acid Phosphatase (=PAP=y); 16. Bone metastases (=BM=F16) (0=no, 1=yes); 17. Date of study (S-date=z17). In the data set there are some attribute and continuous variables. In the current study, DBP is treated as the dependent or response variable, and the rest others are treated as the explanatory or dependent factors/ variables.
Statistical Methods
The considered response variable DBP is identified as heteroscedastic as the under taken PC data set is physiological. Therefore, the heteroscedastic response DBP can be modeled using stabilizing variance under a suitable transformation, but it is not always stabilized [22]. Note that the dependent variable DBP is nonconstant variance, which can be suitably modeled by Joint Generalized Linear Models (JGLMs) under lognormal, or gamma distribution [23,24]. JGLMs is described in the books by Lee et al. [23], and Das [25]. Very shortly, these two JGLMs are described as follows.
Log-normal JGLMs: For the positive response Yi (=DBP) with E(Yi=DBP) = μi (mean) and Var(Yi=DBP) = 2i sμi² = 2i s( ) i V μ say,where 2i s’s are dispersion parameters and V ( ) shows the variance function, commonly,
the log transformation Zi = log(Yi=DBP) is used to stabilize the variance Var(Zi) ≈ 2i s , while it may not be stabilized always [22]. For obtaining an advanced model, JGLMs for the mean and dispersion are derived. Herein for the response DBP, considering log-normal distribution, JGL mean and dispersion models (with Zi = log (Yi=DBP)) are as follows:
E(Zi)= μzi and Var(Zi) = szi²,
μzi=xit β and log (szi²)= git γ,
where xit and git are the explanatory factors/variables vectors attached with the regression coefficients β and γ, respectively.
Gamma JGLMs: For the above stated Yi’s (=DBP), the variance consists of two parts such as V(μi) (depending on the mean parameters) and si² (independent of μi’s). The variance function V( ) indicates the GLM family distributions. For illustration, if V(μ ) =μ , it is Poisson, gamma if V(μ ) = μ² , and normal if V(μ )= 1 etc. Gamma JGL mean and dispersion models for DBP are as follows:
where g(-) and h(-) are the GLM link functions for the mean and dispersion linear predictors respectively, and xit, wit are the vectors of explanatory factors/variables connected to the mean and dispersion parameters, respectively. Maximum likelihood (ML) method is applied for computing mean parameters, and the Restricted ML (REML) method is adopted for obtaining dispersion parameters, which are illustrated in the book by Lee et al., [23].
Statistical & Graphical Analysis
The response DBP is modeled on the rest all explanatory factors/ variables adopting JGLMs using both the distributions such as gamma and log-normal. The best DBP fitted model is accepted based on the lowest Akaike Information Criterion (AIC) value that reduces both the predicted additive errors and the squared error loss [26; p.203-204]. Following the AIC criterion, JGL gamma model fit (AIC= 1433.133) of DBP is better than log-normal fit (AIC= 1448). Both the best DBP fitted JGLMs analysis results are shown in (Table 1). All the included factors in both the models are significant.
Covariates
Gamma fitted model
Log-normal fitted model
Model
estimate
s.e.
t(470)
P-value
estimate
s.e.
t(470)
P-value
Mean
Constant
1.556
0.085
18.34
<0.001
1.544
0.086
17.97
<0.001
HG (z12)
0.008
0.003
2.39
0.017
0.009
0.003
2.61
0.009
Age (z5)
-0.003
0.001
-3.61
<0.001
-0.003
0.001
-3.64
<0.001
SBP (z9)
0.046
0.003
17.27
<0.001
0.045
0.003
16.87
<0.001
Dispersion
Constant
-4.192
0.135
-31.13
<0.001
-4.182
0.134
-31.14
<0.001
S.Stage (F1) 2
-0.452
0.156
-2.89
0.004
-0.475
0.157
-3.03
0.003
CVD Hist. (F8)2
0.256
0.139
1.84
0.060
0.265
0.140
1.89
0.059
BM (F16)2
0.640
0.207
3.09
0.002
0.658
0.207
3.18
0.002
EKG (F11)2
0.336
0.328
1.03
0.305
0.334
0.327
1.02
0.308
EKG (F11)3
0.286
0.143
2.01
0.046
0.334
0.143
2.33
0.020
AIC
1433.133
1448
Table 1: Results for DBP fitting of mean and dispersion models under Gamma & Log-normal distribution.
The data derived DBP models are verified using graphical diagnostic tools. The accepted fitted gamma DBP JGLMs (Table 1) are examined in (Figure 1). (Figure 1a) shows the absolute DBP gamma JGL fitted residuals plot against its predicted values, which is closely a flat straight line, implying that variance is constant with the running means. (Figure 1b) displays the DBP gamma fitted mean model (Table 1) normal probability plot that does not present any lack of fitting. Thus, both the above two (Figure 1a and 1b) show that the DBP gamma fitted JGLMs are very close to the true (unknown) DBP models.
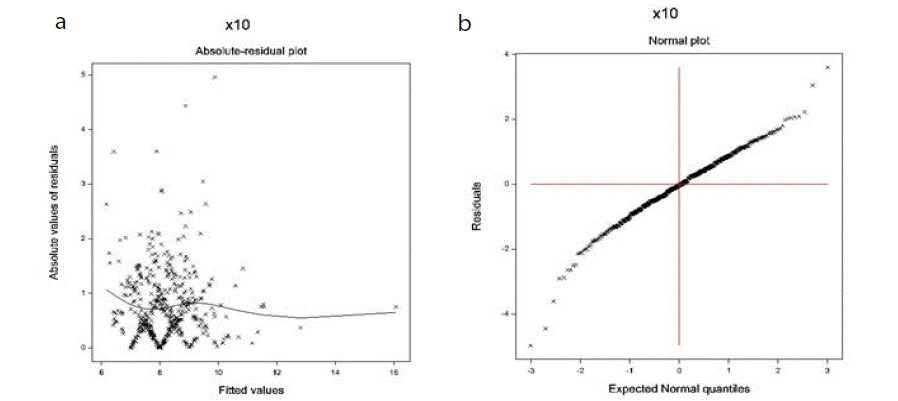
Figure 1: For the JGL gamma DBP fit (Table 1), the (a) absolute residuals plot against the DBP fitted values, and (b) the normal probability plot for the DBP
mean model.
Results and Discussions
Results
Both the summarized DBP fitted findings from JGLMs analysis are shown in (Table 1). It is found that the gamma fitted DBP models are better, so its mean and dispersion fitted results are presented herein. From the gamma fitted DBP mean model, it is derived that mean DBP is directly associated with HG (P=0.017), and SBP (P<0.001), while it is negatively associated with the subject’s age (P<0.001). Variance of DBP is negatively associated with the subject’s stage (P=0.004), while it is positively associated with CVD history (P=0.060), PC patients with BM status (P=0.002), heart patients identified by EKG status (P=0.046). Almost similar results are derived in the log-normal DBP fitted mean and variance models.
JGL gamma fitted DBP mean model (Table 1) is
μ = exp 1.556 + 0.008 HG --0.003 Age + 0.046 SBP ,
and the JGL gamma fitted DBP dispersion (s² ) model (fromTable 1) is
Discussions
In the above, DBP analysis results are displayed along with the selected mean and variance gamma fitted DBP models. From the above gamma fitted DBP mean model, it is observed that mean DBP is directly associated with HG (P=0.017), concluding that DBP rises as the HG increases. Also, mean DBP is directly associated with SBP (P<0.001), implying that DBP rises as the SBP increases for the PC patients. This is observed in practice. On the other hand, mean DBP is inversely associated with the subject’s age (P<0.001), interpreting that mean DBP is higher at the lower age group of PC patients than the older. Note that the minimum age of the considered PC patients is 48 years, while the maximum age is 88 years. Within this age group (48 to 88 years), it is derived herein that DBP is higher in the lower age group PC patients than the higher, which is observed in practice.
From the variance model, it is derived herein that variance of DBP is inversely associated with the subject’s stage (0= no cancer; 1= PC) (P=0.004), concluding that DBP is more scattered for the normal patients than PC patients. It shows that variance of DBP is not associated with the PC patients. Variance of DBP is directly associated with CVD history (0=no, 1=yes) (P=0.060) PC patients, implying that it is more scattered for the CVD history PC patients than the subjects without CVD. It is directly associated with PC patients with BM status (0=no, 1=yes) (P=0.002), interpreting that DBP is more scattered for the PC subjects with BM than without BM. Also, DBP variance is directly associated with PC subject with heart patients identified by EKG status (0=normal; 1=benign; 2= rhythmic disturb & electrolyte; or heart block; or conduction; or heart strain; or old Myocardial Infarction (MI); or recent MI) (P=0.046) at third level, indicating that DBP is more scattered for the PC subject with heart patients at third level than the others.
The derived results of DBP associations with other cardiac and PC risk factors are discussed for both the mean and dispersion models. The direct association between DBP and SBP is well-known, which is established herein for the PC subjects also. In addition, it shows that DBP is higher for the younger PC subjects than senior, which is commonly observed. Therefore, it supports the wellknown results. The other outcomes of DBP associations in this report are very rarely pointed out in the previous articles [1,2,9- 15,17,18]. Specially, the outcomes in the DBP dispersion model are rarely pointed out in any previous articles. Practically, most of the earlier articles used percentage counts, statistical correlation, simple and multiple regression, which are not appropriate to identify the associations of DBP with the other factors [1,9-13,15-17]. Therefore, the current findings are not pointed out in any previous articles. Interested reviewers and readers can examine these reported results using the data set, which is pointed in the material section. Most of the reported results herein related to DBP analysis for the PC subjects are completely new in the PC literature.
Conclusions
The DBP associations with anatomical, biochemical, and disease clinical history of the subjects are discussed in the current article using stochastic modeling. The best fitted model is taken examining the graphical diagnosis, lowest AIC, comparison of two models, and the small standard error of the estimates. The reported results are based on the two possible selected best models. Both the models show similar interpretations. Therefore, the research shows a greater faith in the current findings of the PC data set. The article shows many new interesting results in the PC literature, which are very useful to the common men, researchers and medical practitioners. It is concluded herein that mean DBP is independent of PC risk factors, while it is observed that DBP is highly scattered for PC patients with BM. For PC patients with hypertension, care should be taken on DBP, SBP and HG only.
Conflict of Interest
The authors confirm that this article content has no conflict of interest.
Acknowledgement
The authors are very grateful to the principal data investigators D.P. Byar (National Cancer Institute), who provided the data freely for scientific study.
References
- Stanaway JD, Afshin A, Gakidou E, Lim SS, Abate D, et al. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks for 195 countries and territories, 1990–2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018; 392: 1923-1994.
- Leong DP, Fradet V, Shayegan B, Duceppe E, Siemens R, et al. Cardiovascular Risk in Men with Prostate Cancer: Insights from the RADICAL PC Study. The Journal of Urology. 2020: 203: 1109-1116.
- Hsing AW, Chokkalingam AP. Prostate cancer epidemi¬ology. Frontiers in Bioscience. 2006; 11: 1388-1413.
- Batta A, Panag KMDS. Singh J. Diagnosis of prostate cancer --- Role of biomarkers. Int J Cur Biomed Phar Res. 2012; 2: 339-345.
- Jonušasa J, Drevinskaitea M, Patašiusa A, Kinciusd M, Janulionisb E, Smailytea G. Androgen-deprivation therapy and risk of death from cardiovascular disease in prostate cancer patients: a nationwide lithuanian population based cohort study. The Aging Male. 2022; 25: 173-179.
- Stikbakke E, Schirmer H, Knutsen T, Stoyten M, Wilsgaardet al. Systolic and diastolic blood pressure, prostate cancer risk, treatment, and survival. The PROCA-life study. Cancer Med. 2022; 11: 1005–1015.
- Christakoudi S, Kakourou A, Markozannes G, et al. Blood pressure and risk of cancer in the European Prospective Investigation into Cancer and Nutrition. Int J Cancer. 2020; 146: 2680-2693.
- Liang Z, Xie BO, Li J, Wang X, Wang S, et al. Hypertension and risk of prostate cancer: a systematic review and meta-analysis. Sci Rep. 2016; 6: 31358.
- Seretis A, Cividini S, Markozannes G, et al. Association between blood pressure and risk of cancer development: a systematic review and metaanalysis of observational studies. Sci Rep. 2019; 9: 8565.
- Wilk M, Wasko-Grabowska A, Szmit S. Cardiovascular Complications of Prostate Cancer Treatment. Front Pharmacol. 2020; 11: 555475.
- Davis MK, Rajala JL, Tyldesley S, Pickles T, Virani SA. The Prevalence of Cardiac Risk Factors in Men with Localized Prostate Cancer Undergoing Androgen Deprivation Therapy in British Columbia, Canada. Journal of Oncology. 2015; 2015: 820403.
- Zhou B, Bentham J, Di Cesare M, et al. Worldwide trends in blood pressure from 1975 to 2015: a pooled analysis of 1479 population-based measurement studies with 19•1 million participants. Lancet (London, England). 2017; 389: 37-55.
- Sfanos KS, Yegnasubramanian S, Nelson WG, De Marzo AM. The inflammatory microenvironment and microbiome in prostate cancer development. Nat Rev Urol. 2018; 15: 11-24.
- Arthur R, Williams R, Garmo H, et al. Serum inflammatory markers in relation to prostate cancer severity and death in the Swedish AMORIS study. Int J Cancer. 2018; 142: 2254-2262.
- Liu, Y. et al. Does physical activity reduce the risk of prostate cancer? A systematic review and meta-analysis. Eur Urol. 2011; 60:1029–1044.
- Pai PY, Hsieh VCR, Wang CB, Wu HC, Liang WM, et al. Long term antihypertensive drug use and prostate cancer risk: A 9-year populationbased cohort analysis. Int J Cardiol. 2015; 193:1–7.
- Beebe-Dimmer JL, Dunn RL, Sarma AV, Montie JE, Cooney KA. Features of the metabolic syndrome and prostate cancer in African-American men. Cancer. 2007; 109: 875–881.
- Martin RM, Vatten L, Gunnell D, Romundstad P. Blood pressure and risk of prostate cancer: Cohort Norway (CONOR). Cancer Causes Control. 2010; 21: 463–472.
- Byar DP, Corle DK. Selecting optimal treatment in clinical trials using covariate information. Chronic Diseases. 1977; 30: 445-469.
- Byar DP, Green SB. The choice of treatment for cancer patients based on covariate information: application to prostate cancer. Bull. Cancer, Paris. 1980; 67: 477-488.
- Andrews DF and Herzberg AM. Data, A Collection of Problems from Many Fields for the Student and Research Worker. New York: Springer-Verlag, 1985.
- Myers RH, Montgomery DC, Vining GG. Generalized Linear Models with Applications in Engineering and the Sciences. New York: John Wiley & Sons, 2002.
- Lee, Y, Nelder JA, PawitanY. Generalized Linear Models with Random Effects (Unified Analysis via H–likelihood) (second edition). Chapman & Hall, London, 2017.
- Das RN and Lee Y. Log-normal versus gamma models for analyzing data from quality-improvement experiments. Quality Engineering 2009; 21: 79-87.
- Das RN. Robust response surfaces, regression and positive data analyses. Chapman & Hall, London, 2014.
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, Springer-Verlag, 2009.