Efficiency Evaluation and Spatial Autocorrelation Analysis of Primary Health Care Resources Distribution: The Panel Three-Stage DEA Model

Liu YL; Xu RX; Meng XH; Ye YP; Xu CM

Research Article

J Community Med Health Care. 2022; 7(1): 1057.

Efficiency Evaluation and Spatial Autocorrelation Analysis of Primary Health Care Resources Distribution: The Panel Three-Stage DEA Model

Liu YL^1,2, Xu RX¹, Meng XH¹, Ye YP¹ and Xu CM^2,3*

¹School of Humanity and Management, Zhejiang Chinese Medical University, China

²Ningbo Municipal Hospital of TCM Affiliated Hospital, Zhejiang Chinese Medical University, China

³School of Law, Zhejiang University, China

*Corresponding author: Xu CM, College of Humanity and Management, Zhejiang Chinese Medical University, Gaoke Road, Fuyang District, Hangzhou City, Zhejiang Province, China

Received: June 27, 2022; Accepted: August 01, 2022; Published: August 08, 2022

Abstract

Objective: To analyse the distribution of Primary Health Care (PHC) in efficiency among provinces from 2010 to 2019 in China, to examine the factors influencing performance, and to describe the spatial agglomeration characteristics of allocation efficiency, so as to optimize and balance the utilization thereof.

Method: Using a panel Three-stage DEA comparative analysis model to describe factors that may lead to high efficiency, combined with a descriptive study for spatial agglomerating features of provinces using Spatial autocorrelation analysis.

Results: The overall performance of PHC distribution efficiency is unreasonable, with an average comprehensive technical efficiency of 0.688 from 2010 to 2019. The external and management noise had a significant impact on the efficiency of PHC resource allocation. The increase in per capital GDP could enhance the efficiency, but the dependence ratio of the elderly population and the rate of urbanization were inversely. The effectiveness of PHC allocation had spatial agglomeration features. Moran’s I index was the lowest in 2016 (0.293) and the highest in 2019 (0.421) at the significance level of 1%. The Getis_Ord GI* index demonstrates that the general level of spatial agglomeration had improved, with the number of cluster provinces increasing from 11 to 15.

Conclusion: The PHC distribution efficiency should be improved, the establishment of balanced eastern, central and western regions should be encouraged, and a new PHC ecosystem should be established. Further, new patterns should be created in the geographic area of primary health care, and citizens’ access to medical services should be increased.

Keywords: Regional distribution efficiency; Panel three-stage DEA; Spatial autocorrelation analysis

Introduction

Primary Health Care (PHC) is one of the most effective and efficient strategies to maintain good health [1,2]. Increasing the input of PHC allows people to access the health care they need more easily, thereby compensating for the fact that hospital-centered health-care systems require high costs but are unable to fulfill people’s needs and are not sustainable in the long term [3]. Due to rising prevalence and economic constraints, effective PHC levels are required [4]. As such, PHC competency should be improved. In China community health service centers and community health service stations are located primarily in cities, while township health centers and village clinics are located primarily in rural areas. Despite the significant increase in total PHC resources over the last ten years, the number of grassroots medical and health institutions, beds, and personnel at the end of 2020 increased by 7.58 percent, 38.35 percent, and 32.23 percent, respectively, compared with 2010. However, there was a significant disparity between PHC institutions and hospitals. By the end of 2020, PHC institutions accounted for 94.83 percent of total national medical and health institutions, or 31.96 times the total number of hospitals. Further, there is an unbalanced geographic distribution of PHC [5] between urban and rural areas, among the three regions, and among various provinces, resulting in disparities in medical service utilization. In summary, grass-roots medical and health resources face issues such as insufficient total amount, unbalanced allocation, and failure to demonstrate the benefits of high accessibility. So, how to optimize the regional distribution of PHC efficiency has become a hot issue that needs to be studied. The allocation efficiency of medical and health resource at the grass-roots level needs to be evaluated from two dimensions: time and space, and the influencing factors need to be studied. Policy solutions should be formulated to improve and balance regional resource allocation efficiency and provide ideas for further assisting decision makers.

The measurement methods adopted in previous studies typically include non-parameter methods such as Data Envelopment Analysis (DEA) and the parameter method as Stochastic Frontier Analysis (SFA). Proposed by Charles and Cooper (1978) to evaluate inputoutput efficiency [6], DEA is a nonparametric linear programming model that solves the problem of heterogeneity among decision making units and is widely used for measuring and comparing hospital and health efficiency. However, Single DEA failed to consider the influence of environmental variables and random errors on efficiency thus resulting in inaccurate measurement. Timmer (1971) pioneered a typical two-stage approach follows a first stage DEA exercise based on inputs and outputs with a second stage regression analysis seeking to explain variation in first stage.1, and several subsequent studies have improved upon Timmer’ Second stage by using limited dependent variable regression techniques, since it can’t strip away the influence of environmental effects and random errors on the efficiency value, Fried (2002) et al. [7] proposed a three-stage DEA model, in which the nonparametric DEA model was combined with the parametric SFA (Stochastic Frontier Analysis) model. This model not only retains the advantage that DEA does not need to set the overall distribution assumption, but also considers external environmental factors, random disturbance, and management inefficiency, so as to obtain a more realistic efficiency value. Simar and Wilson (2011) verified that in the practice of DEA efficiency estimates are regressed on some environmental variables in a second-stage analysis, and think the second-stage regressions are well-defined and meaningful [8].

DEA and the extended methods thereof have been extensively adopted to measure the differences in health resource distribution efficiency [9,10]. This method of using regression model to analyze influencing factors in the second stage is mainly represented by DEATobit [11-12], which has been widely used in the study of health resource efficiency in recent years [13]. However, although this method can identify the main influencing factors of health resource efficiency, it can’t calculate the exact efficiency value. Although the three-stage method has eliminated the environmental impact and statistical noise, it can re-evaluate the efficiency to obtain more realistic value. At present, it is rarely used in the research of health resource efficiency evaluation. Some scholars use the three-stage DEA method to study hospitals [14]. However, it is only based on crosssectional data, and does not involve the panel data, so it can’t reflect efficiency changes in a long period. In addition, existing research shows that there is a certain spatial agglomeration of medical and health resources [15]. On this basis, this study further analyzes the spatial agglomeration characteristics of the allocation efficiency of primary medical resources, thus expanding the research scope of evaluating PHC efficiency in different provinces.

Materials and Methods

Data Source and Defined Variable

The data used in the present study were obtained from the China Health Statistics Yearbook (2011-2020) and the China Statistics Yearbook (2011-2020). According to the regional classification standard of the national statistics, 31 provinces (excluding Taiwan, Hong Kong and Macao) in China are divided into three regions: eastern, central and western.

Variable indicators that are aligned with the characteristics of medical services have been widely adopted in research on health resources [16,17]. Inputs, Outputs, and the Environment index are the three dimensions [18,19]. The number of medical Institutions (IN), the Number of Beds (BN), and the Number of Personnel (PN) are among the input dimensions. The numbers of medical institutions and beds are sensitive indicators of the scale of medical resources. The input personnel comprise not only physicians, nurses, laboratory staff, radiology staff, and other health and technical staff, but also administrative, logistics, and other support departments. That because medical practice requires a high level of team collaboration [20]. The Number of Outpatients (ON) and Discharges (DN) are the output dimension variables, which provide the most direct indication of the efficiency of outpatient (emergency) diagnosis [21]. The number of visits and discharges are the output dimension variables [22].

In the present study, the main focus was on the characteristics that have a large impact on efficiency, are not subject to the sample’s subjective control, and are difficult to modify in a short period of time when choosing environmental dimension variables [23,24]. The impacts of economic development, policy direction, social development, and demographic variables on medical and health resource allocation were also analyzed. Four factors were specified to assure the comprehensiveness of the selection of environmental variables and data availability. To measure the level of local economic growth, Regional GDP per capital (RPGDP) was used. In general, the stronger the financial capability and the greater the involvement in medical and health development, the higher the level of local economic development. The Density of Population (DP) per unit area of land is directly tied to the development of local economic, political, and social systems. The Elderly Population’s Dependency Ratio (EPDR) reflects the degree of social aging and the overall social burden of the elderly population, influencing the allocation of health resources. Meanwhile, the Urbanization Rate (UR) reflects changes in people’s health demands and medical service preferences as cities grow.

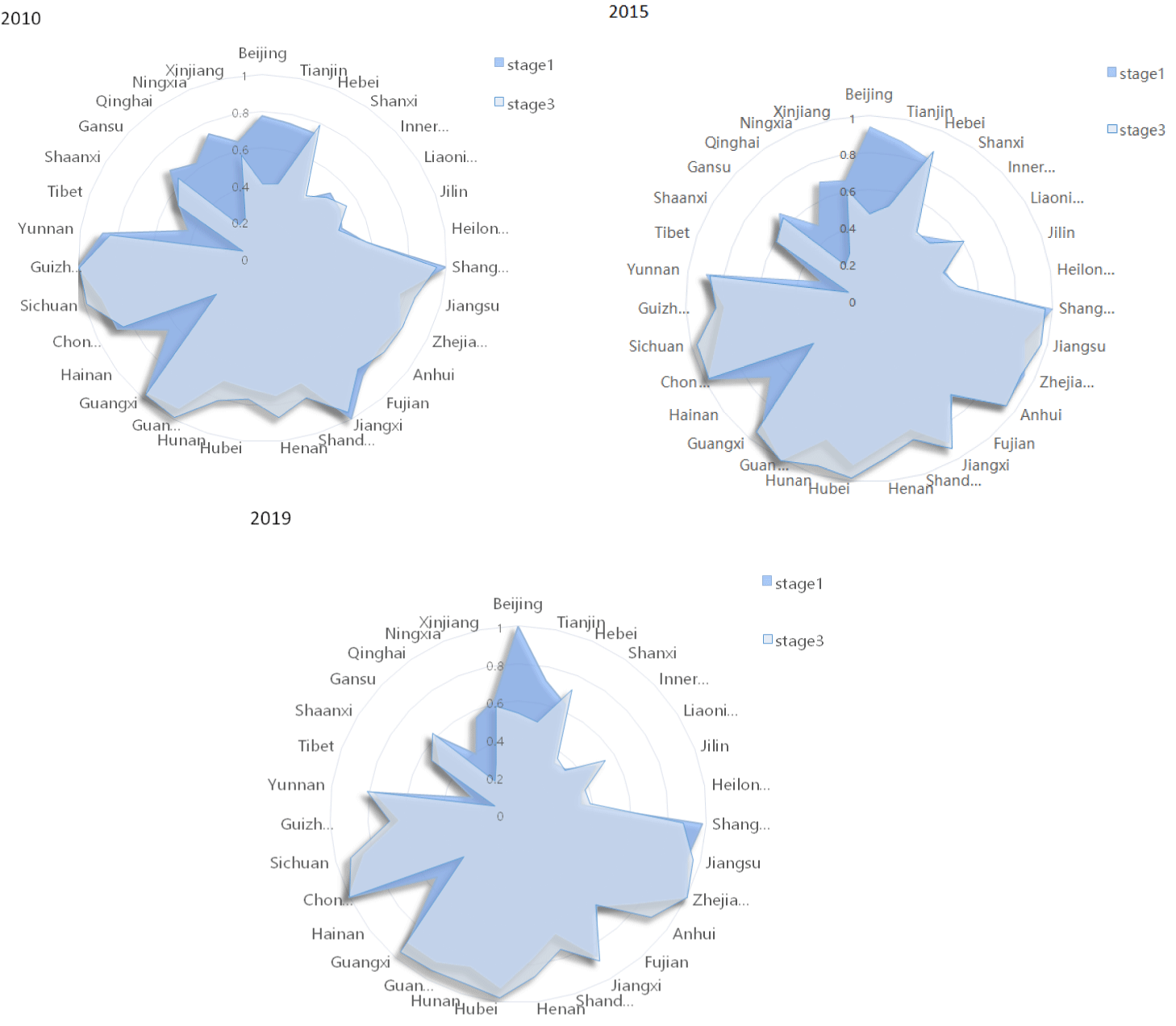
Figure 1: Comparison of comprehensive technical efficiency value of grass-roots medical resources in 31 provinces before and after adjustment in 2010, 2015 and 2019.


    

    

    Figure 1: Comparison of comprehensive technical efficiency value of grass-roots medical resources in 31 provinces before and after adjustment in 2010, 2015

and 2019.

Statistical Method

The Panel Three-stage DEA Model: The classic three-stage DEA model is only applicable to cross-sectional data decisionmaking units, and there are limitations in calculating the efficiency of cross-sectional panel data due to the cutting edge of each year, which renders an uneven surface. As a result, to solve the problem of Frontier heterogeneity, the proposed panel three-stage model method [25] was used to examine and investigate the efficiency. The specific steps are as follows:

The first stage involved building an input-oriented BCC model based on variable return to scale. The cross-year panel data was sorted into cross-sectional data, which means that the same decision-making unit was regarded as a different decision-making unit in each year, so as to obtain the input slack value of each decision-making unit under the unified efficiency frontier. Regarding the traditional DEA-BBC model, there are several theoretical approaches and applications that are not mentioned in the present study.

The second stage involved using SFA regression model to decompose Stage 1 Slack. Since the explained variables were the number of PHC institutions, personnel, and beds calculated in the first stage, and four environmental variables such as per capital GDP were used as explanatory variables for regression analysis to adjust the effects of random errors and environmental factors, the SFA regression function of the input slack variable of PHC efficiency was created as follows:

S_nit = f(Z_it ; β_nt) + μ_nit + ν_nit (1)

In Formula (1), S_nit is the total slack variable of PHC in the nth year of the ith Province in the t year; Z_nitis the environmental explanatory variable;β_nt is the parameter to be estimated of the environmental variable; f(Z_it;β_nt) indicates the influence of environmental factors on input relaxation variables. μn_it + v_nit is a mixed error term. v_nit represents the random interference term, which is generally assumed to obey the standard normal distribution, V~ N(0, σ²vi) and μ_ni is the management inefficiency term, which is generally assumed to obey the truncated normal distribution μ~N(μ σ²vi) According to whether the management inefficiency item changes over time, panel SFA was separated into two types: the Time-Varying Dependent Regression Model (TVDM) and the Time Independent Model (TIM). In the TVDM, the management inefficiency term remains constant across periods, and it is independent with the random disturbance. Assuming μ_i=exp{-n(t-Ti)} (η is the time decay coefficient, and Ti is the last period of the decision-making unit), if η is significant and greater than 0, the non-efficiency level of the DMU decreases with time, which means the efficiency level will be higher and higher; but if η is significant and smaller than 0, the DMU’s non-efficiency level rises over time, implying that the efficiency level falls. If the efficiency level is non-significant or 0, a TIM was used. Moreover, letting γ=σ²un/(σ²un+σ²vn) the closer γ is to 1, the greater σ²un is, indicating that the management inefficiency factor is a leading factor. The closer γ is to 0, the greater σ²vn is, illustrating that the random error factor is a leading factor [26,27].

Jondrow et al. [28] used Fried’s method to decompose the mixed error term (the formula is omitted), and the management inefficiency term was decomposed according to the method proposed by Luo Dengyue [29]. The formula is as follows:

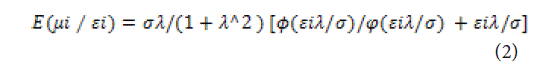
In Formula (2),λ=σμ/σv εi=vni,σ²=σμ²+σv²,ø,ø are the density distribution functions of the standard normal distribution, respectively.

The environmental factors and random interference factors of each province were adjusted to the same state. The adjustment formula of SFA regression model to the original input is as follows:

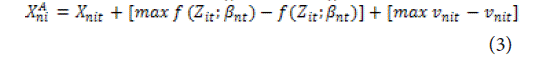
$https://latex.codecogs.com/svg.image?\textit{X}_{ni}^{A}$ is the input value after factor adjustment of the nth Province in stage I.

The third stage involved recalculating the resource allocation efficiency value of grass-roots medical and health institutions in each province by replacing the adjusted input index value of Formula (3) with the original value (1).

Spatial Autocorrelation Analysis

Global spatial autocorrelation was used to examine the entire spatial distribution pattern of the efficiency value of primary medical resources in 31 provinces, indicating the spatial reliance. Local spatial autocorrelation was used to reflect the spatial correlation between each province’s efficiency value and the nearby region, and could also be used to determine the contribution of each spatial unit’s efficiency observation value. Moran’s I [30,31], Getis_ord Gi* statistics [32] are the most commonly used statistics for testing global spatial and local autocorrelation respectively. Formulas (4) and (5) are the two statistics formulas.

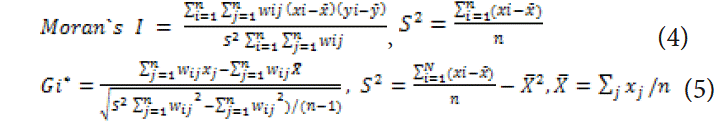
In the formula (4) and (5), Where S2 is the sample variance, n represents the number of provinces, xi, yi represents the efficiency value of PHC distribution in each province, and $https://latex.codecogs.com/svg.image?\tfrac{}{X},\tfrac{}{Y}$ represents the average efficiency in the spatial weight matrix. W_ij is the spatial weight matrix between element i and j, and

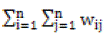
represents the sum of all spatial weight matrices. is the averaged value of all provinces.

The value range of the global Moran’s I was [-1,1]. If Moran’s I>0, there was a geographic positive correlation in the distribution of PHC in each province, and the closer Moran’s I was to 1 and the more substantial I is, the more prominent the spatial agglomeration features were.

Gi* statistics returned for each element in the data set are Z score. It is used to identify statistically significant spatial clusters of high values (hot spots) and low values (cold spots).The higher the Z score, the tighter the clustering of high values (hot spots). For statistically significant negative Z score, the lower the Z score, the tighter the clustering of low values (cold spots) spots. Getis_ord Gi* index (GI* index) cold and hot spot map directly depicted the agglomeration status of PHC resource distribution in each province. A rook geographical adjacency weight matrix was established. In the present study. That is, if two spatial units ( and ) were adjacent, the corresponding element was 1, otherwise it was 0. Considering that Hainan is geographically adjacent to Guangdong, the adjacency state was modified to 1 to avoid missing values.

Results and Discussion

Results

In the study, the allocation efficiency of PHC resources in 31 provinces from 2010 to 2019 was measured. The input-output correlation selected in the study meets the requirements of data envelopment analysis. Table 1 shows the statistical descriptive results of variables, and illustrates that there was a significant variation between the highest and minimum values of each variable. For instance, the regional GDP per capita demonstrates the disparity with a standard deviation of 2.63, a maximum value of 1.29 per head in Beijing in 2019, and a minimum value of 164.2 per head in Guizhou Province in 2010.

Table 1: Descriptive statistical result of variables.








  

    Type

    Name

    Unit

    Abbreviation

    Mean

    Standard deviation

    Min

    Max

  

  

    Input indicators

    Primary Medical and health    institution number

    Ten thousand

    IN

    2.982

    2.120

    0.388

    0.822

  

  

    Number of beds in primary medical and health    institutions 

    Ten thousand

    BN

    4.542

    3.489

    0.246

    14.830

  

  

    Number of personnel in    primary medical and health institutions

    Ten thousand

    PN

    11.736

    8.053

    0.805

    34.919

  

  

    Output indicators

    The number of outpatient in primary medical and    health institutions 

    One hundred million 

    ON

    1.364

    1.120

    0.060

    4.386

  

  

    Number of discharged patients in primary medical    and health institutions 

    Ten thousand 

    DN

    1.345

    1.2473

    0.02

    5.20

  

  

    Environmental variables

    Regional GDP per capital

    Ten thousand yuan

    RPGDP

    5.00

    2.63

    1.29

    16.42

  

  

    The density of population

    Per sq. kilo 

    DP

    2.82

    1.17

    0.52

    5.82

  

  

    The elderly population's dependency ratio 

    % 

    EPDR

    13.59

    3.38

    6.71

    23.82

  

  

    the urbanization rate 

    %

    UR

    56.09

    13.39

    22.67

    89.6

  

  

    Note: Obs=310, id=31






Table 1: Descriptive statistical result of variables.

Analysis on the allocation efficiency of national PHC resources: Considering only the original input-output data, we conduct the first stage of DEA-BCC analysis on the allocation efficiency of PHC resources. Owing to space constraints, only the average efficiency of grass-roots medical resource allocation in each province from 2010 to 2019 was provided, as well as the return to scale in 2019 (Table 2). Without accounting for external environmental factors or random interference, the allocation of grass-roots medical resources in each province was estimated to be essentially good, with an average comprehensive efficiency of 0.726, an average pure technical efficiency of 0.803, and an average scale efficiency of 0.906. The average comprehensive efficiencies of the eastern, central, and western regional sectors were 0.803, 0.688, and 0.681, respectively. Shanghai, Chongqing, and Jiangsu were among the top three provinces in terms of total efficiency. Except for the scale efficiencies of Beijing, Zhejiang and Chongqing is unchanged, most provinces were in the state of increasing returns to scale.

Table 2: Comparison of average value of PHC resource allocation efficiency in stage I and stage III from 2010 to 2019.








  

    Region

    Provinces

    stage1 

    stage III 

  

  

    TE

    PTE

    SE

    Returns to Scale

    TE

    PTE

    SE

    Returns to Scale

  

  

    Eastern

    Beijing

    0.912

    0.962

    0.946

    -

    0.480

    0.973

    0.493

    IRS

  

  

    Tianjin

    0.807

    0.984

    0.820

    IRS

    0.491

    0.983

    0.499

    IRS

  

  

    Hebei

    0.769

    0.776

    0.990

    DRS

    0.832

    0.857

    0.970

    IRS

  

  

    Liaoning

    0.54

    0.552

    0.978

    IRS

    0.576

    0.758

    0.759

    IRS

  

  

    Shanghai

    0.991

    0.997

    0.995

    IRS

    0.940

    0.984

    0.955

    IRS

  

  

    Jiangsu

    0.874

    0.912

    0.958

    DRS

    0.941

    0.953

    0.987

    DRS

  

  

    Zhejiang

    0.937

    0.942

    0.995

    -

    0.926

    0.974

    0.950

    -

  

  

    Fujian

    0.707

    0.721

    0.980

    IRS

    0.698

    0.841

    0.830

    IRS

  

  

    Shandong

    0.721

    0.869

    0.835

    DRS

    0.797

    0.914

    0.875

    DRS

  

  

    Guangdong

    0.943

    0.982

    0.961

    DRS

    0.976

    0.991

    0.985

    DRS

  

  

    Hainan

    0.636

    0.859

    0.741

    IRS

    0.365

    0.966

    0.379

    IRS

  

  

    Mean

    0.803

    0.869

    0.927

    

    0.729

    0.927

    0.789

    

  

  

    Central

    Shanxi

    0.400

    0.416

    0.961

    IRS

    0.424

    0.606

    0.699

    IRS

  

  

    Jilin

    0.423

    0.460

    0.919

    IRS

    0.416

    0.732

    0.569

    IRS

  

  

    Heilongjiang

    0.462

    0.509

    0.907

    IRS

    0.483

    0.748

    0.645

    IRS

  

  

    Anhui

    0.855

    0.868

    0.985

    DRS

    0.903

    0.947

    0.952

    IRS

  

  

    Jiangxi

    0.911

    0.923

    0.986

    DRS

    0.932

    0.973

    0.957

    IRS

  

  

    Henan

    0.780

    0.879

    0.888

    DRS

    0.868

    0.929

    0.936

    DRS

  

  

    Hubei

    0.869

    0.908

    0.960

    DRS

    0.937

    0.953

    0.982

    DRS

  

  

    Hunan

    0.801

    0.906

    0.887

    DRS

    0.934

    0.954

    0.980

    DRS

  

  

    Mean

    0.688

    0.734

    0.937

    

    0.737

    0.855

    0.840

    

  

  

    Western

    Chongqing

    0.955

    0.964

    0.991

    -

    0.949

    0.994

    0.955

    -

  

  

    Guangxi

    0.878

    0.884

    0.994

    DRS

    0.926

    0.943

    0.982

    DRS

  

  

    Sichuan

    0.873

    0.946

    0.924

    DRS

    0.970

    0.981

    0.988

    DRS

  

  

    Guizhou

    0.781

    0.790

    0.985

    IRS

    0.813

    0.881

    0.915

    IRS

  

  

    Yunnan

    0.860

    0.869

    0.991

    IRS

    0.856

    0.932

    0.920

    IRS

  

  

    Tibet

    0.305

    0.773

    0.396

    IRS

    0.120

    0.908

    0.132

    IRS

  

  

    Gansu

    0.688

    0.701

    0.981

    IRS

    0.665

    0.879

    0.757

    IRS

  

  

    Qinghai

    0.523

    0.816

    0.635

    IRS

    0.233

    0.958

    0.243

    IRS

  

  

    Shaanxi

    0.545

    0.561

    0.970

    IRS

    0.575

    0.734

    0.784

    IRS

  

  

    Overall

    Ningxia

    0.670

    0.984

    0.680

    IRS

    0.275

    0.988

    0.278

    IRS

  

  

    Xinjiang

    0.644

    0.708

    0.909

    IRS

    0.600

    0.840

    0.714

    IRS

  

  

    Inner Mongolia

    0.457

    0.487

    0.936

    IRS

    0.431

    0.704

    0.610

    IRS

  

  

    Mean

    0.681

    0.790

    0.866

    

    0.618

    0.895

    0.690

    

  

  

    

    0.724

    0.798

    0.910

    

    0.695

    0.892

    0.773

    

  

  

    Note: TE =PTE *SE, TE represents comprehensive efficiency; PTE    represents pure technical efficiency; SE represents scale efficiency; DRS    represents decreasing returns to scale; and IRS represents increasing returns    to scale.






Table 2: Comparison of average value of PHC resource allocation efficiency in stage I and stage III from 2010 to 2019.

Influence of environmental variables on input slack variables: Since provinces have such disparities in economic, social, and demographic development, investigation into the impact of environmental variables on input slack variables and the adjustment of input variables are crucial. A panel SFA regression model was constructed using the slack values of the number of primary medical institutions, beds, and personnel calculated in the first stage as dependent variables. Moreover, the independent variables of per capital GDP, population density, total dependency ratio, and urbanization rate were used as independent variables, and the regression result is in (Table 3). The LR test statistics of the model passed the significance test showing that the estimation results were acceptable. Further, the sum values corresponding to the three input slack variables passed the significance test, with values greater than 0.8, indicating that management inefficiency and random error both had an impact on the input slack value, with management inefficiency having a significant effect. Moreover, with the exception of population density, all other environmental variables passed the t-test, indicating that external environmental factors had a significant impact on the input redundancy of PHC resources.

Table 3: SFA analysis results in stage II.








  

    Variables 

    IN Input Slack coefficient 

    t-Test 

    BN Input Slack coefficient 

    t-Test 

    PN Input Slack coefficient 

    t-Test 

  

  

    Constant

    -7688.017***

    -7.087

    -8551.558***

    -233.632

    -17531.422***

    -269.018

  

  

    RPGDP

    -666.185***

    -4.380

    -721.484**

    -3.571

    -1522.546**

    -3.245

  

  

    DP

    273.137

    0.669

    -226.371

    -0.451

    152.352

    0.132

  

  

    EPDR

    189.9579**

    1.970

    655.02715***

    5.430

    1048.2228***

    3.777

  

  

    UR

    117.5938***

    4.490

    74.969472**

    2.075

    182.13222**

    2.128

  

  

    s2

    231416450

    231402920

    111120090

    111119590

    731045840

    731045690

  

  

    g

    0.961

    295.328

    0.819

    53.309

    0.862

    73.742

  

  

    Log likelihood function

    -2987.584

    

    -3093.467

    

    -3343.898

    

  

  

    LR test of the one-sided error

    587.306

    

    215.212

    

    277.557

    

  

  

    Note: ***,    **, * represent significance under 1, 5, 10% significance    levels respectively.






Table 3: SFA analysis results in stage II.

Spatial autocorrelation analysis: Global spatial autocorrelation analysis was used to measure the overall spatial agglomeration level of primary medical resource allocation efficiency. The global Moran’s index (Moran’s I) values of efficiency from 2010 to 2019 were positive and all passed the significance test (p<0.01). In terms of the change trend of Moran’s I, there was a slow increase from 0.326 in 2010 to 0.385 in 2012, then a rapid decrease, before a low of 0.293 in 2016. Finally, there was a rapid rebound to 0.421 in 2019. Refer to the changing trend of Moran`s I scatter diagram of the efficiency, most provinces are located in the first and the third quadrant, showing high-high concentration and low-low concentration. The results show that the trend of spatial concentration has been gradually strengthened in the past ten years. Only a few sporadic provinces exhibited high-low concentration and low-high concentration in the second and fourth quadrants, that is, there was spatial heterogeneity, mainly in Hainan, Hebei and Sichuan provinces.

After determining the global spatial agglomeration level, local spatial autocorrelation analysis was conducted to explore the agglomeration characteristics of each spatial unit. As shown in (Table 4), the distribution of hot and cold spots in Getis_Ord Gi* index generally improved from 2010 to 2019, and the agglomeration provinces increased from 11 to 15 provinces, including 8 to 10 hot spots and 3 to 5 cold spots.

Table 4: Getis_Ord Gi* index distribution table of hot and cold spots.








  

    Distribution type

    2010

    2019

  

  

    Number

    provinces

    Number

    provinces

  

  

    Hot spots

    8

    Hunan***, Jiangxi**,    Guizhou **, Guangxi**, Anhui*, Jiangsu*,    Fujian*

    10

    Jiangxi**, Hunan**,    Guizhou **, Hubei **, Anhui **, Jiangsu*,    Fujian*, Guangxi*, Zhejiang* and Shanghai *

  

  

    Cold point

    3

    Xinjiang * *,    Inner Mongolia *, Gansu *

    5

    Inner Mongolia ***,    Xinjiang**, Gansu*, Jilin*, Heilongjiang*

  

  

    No significant

    20

    slightly

    16

    Slightly

  

  

    Note: *means p<0.05, **means p<0.01 and ***    means p<0.001.






Table 4: Getis_Ord Gi* index distribution table of hot and cold spots.

Discussions

Provincial and regional comparison of the efficiency of PHC resources in 2009-2019: Compared with the first stage, there was little reduction in the final comprehensive efficiency and the pure technical efficiency significantly improved, but the scale efficiency decreased. Guangdong, Shanghai, and Jiangsu were the top three in terms of overall efficiency; while the technical capacity and management level in Tibet, Shanxi, and Jilin were all low. With the exception of Tianjin and Shanghai, the pure technical efficiencies of all provinces improved, signifying that the technical capability and management levels improved to varied degrees in the majority of provinces. Chongqing, Guangdong, and Tianjin were among the most efficient provinces, with Jilin, Heilongjiang, and Inner Mongolia seeing the most growth. In scale efficiency, of which Beijing, Ningxia and Qinghai had the largest decline, indicating that the improvement of the technical efficiency of grass-roots medical and health resources was not enough to offset the decline in scale efficiency. Finally, in terms of returns to scale, in 2019, the number of provinces with increasing returns to scale increased from 17 to 21, indicating that the overall efficiency had improved significantly, but there was still a certain gap from reaching the efficiency frontier.

From the perspective of the eastern, central and western regions, in terms of comprehensive technical efficiency, the eastern region had a highest value before the adjustment, but a slightly lower value to the central region after the adjustment, indicating that the comprehensive management efficiency level of the central region was underestimated. The pure technical efficiency of the three major regions significantly improved after the adjustment, among which the eastern region exhibited the most improvement, and the western region exhibited slightly better improvement than the central region after adjustment. In terms of scale, the central region was the highest, followed by the eastern region, while the western region was the lowest. In summary, the eastern region needs to pay more attention to scale efficiency, the central region needs to focus on the improvement of technical ability, and both the management level and scale efficiency in the western region need to be further improved.

Analysis of factors affecting the efficiency of PHC: The decay coefficient for the panel SFA regression model had to be tested first to decide if TVDM or the TIM should be used. Since the decay coefficient calculated this time is not significant, TI model is adopted. Additionally, according to the positive and negative judgment of the environmental variable coefficient, if the coefficient was positive, the variable had a positive effect on the input slack variable, which reduced the allocation efficiency of grass-roots medical resources, and vice versa. Notably, even the t-value test was not significant; there was still a directional effect.

To be specific, as shown in Table 3, in terms of economic and environmental impact, per capital GDP had a significant negative effect on the slack variables of the number of PHC institutions, beds, and personnel, indicating that improving the regional economic environment was conducive to the capacity of PHC at all levels. At the same time, people in economically developed areas had more health needs for which they could afford, promoting the effective. In terms of social and environmental factors, population density had no significant effect on the slack variables of the three inputs, but had a negative effect on the slack of the number of beds, indicating that the problem of an insufficient proportion of beds in grass-roots medical institutions still existed. Such findings suggest that high population density areas are primarily concentrated in central cities with abundant public hospital resources, and People prefer large hospitals to small, community-based medical and health institutions. Thus, population density tends to stifle the efficiency with which the number of grassroots medical institutions and people is allocated. In terms of population burden, the elderly dependency ratio has a strong positive effect on all input slack variables, showing that the load of basic medical services increased as the population aged. As an example, government reports show that hypertension is prevalent in senior persons over the age of 60 with a prevalence rate of 58.3 percent. Diabetes affects 19.4% of people in China [33], reducing the efficiency. Finally, the degree of urbanization had a strong positive impact on the slack variables of various inputs, implying that the greater the rate of urbanization, the poorer the efficiency. The development of urbanization resulted in a significant loss of community-based medical facilities. For instance, according to statistics, the number of township hospitals declined from 38,000 to 35,800, while, the number of hospitals expanded significantly, rising from 20,900 to 35,400 between 2010 and 2020.

The PHC resources are set up according to administrative divisions, with obvious geographical characteristics, consistent with the first law of geography, “everything is related, and similar things are more closely related” [34]. As found in existing empirical studies, there are spatial effects in the efficiency of health resource allocation, the results of this study reveal that at the significance level of 1%, there was a positive spatial autocorrelation between provinces, and most provinces exhibit a state of spatial agglomeration. In terms of the change trend of Moran’s I over the past decade, there was a slow increase from 0.326 in 2010 to 0.385 in 2012, then a rapid decrease, before a low of 0.293 in 2016. Finally, there was a rapid rebound to 0.421 in 2019.That trend shows an “N” contours, and maintained a rapid and continuous upward trend. Besides, from the perspective of the spatial distribution level of each province in Moran’s I scatter plot, it depicts a progressive increase in geographic aggregation over the last decade. Due to the continuous expansion of public hospitals, the strong siphon effect resulted in the ‘brain drain’ of grass-roots medical and health personnel, which was also reflected in the trend of grass-roots reform. China has placed emphasis on improving public and medical service, according to the country’s grass-roots reform timeline from 2009 to 2015. But from 2015 to the present, the focus has been on establishing a “Medical Unions” in cities and “Medical Communities” in counties, and directing the sinking of medical and health resources. Therefore, through the construction of Health Service Consortiums, a new collaborative relationship of complementary functions and win-win cooperation was built between public hospitals and grass-roots medical and health institutions, which is also consistent with the time period when Moran`s I value rebounded from stabilization.

Additionally, according to the Getis_Ord GI* index, as shown in Table 4, the distribution of cold and hot spots shows that the overall level of spatial agglomeration improved, and the proportion of agglomeration provinces in the total number of provinces rose from 35.48% to 48.39%. The hot spots expanded from Jiangxi to Hubei in the north and Zhejiang and Shanghai in the east, and the center of the cold spots moved eastward from Xinjiang to Inner Mongolia, and then continued to expand eastward to Jilin and Heilongjiang, forming two large gathering areas in the north and south-central areas. The findings indicate that the agglomeration scope of the efficiency continued to expand.

Conclusion

In this study, a panel three-stage DEA model and spatial autocorrelation analysis method was used to measure and analyze the efficiency and the influencing factors of PHC resources in 31 provinces in China from 2010 to 2019. There were disparities between provinces, and the allocation among the eastern, central, and western regions was imbalanced. The external environment and managerial noise had a significant impact on the efficiency of primary medical resource allocation, and the redundancy of numerous input components was prevalent. The degree of spatial agglomeration gradually increasing from 2010 to 2019.

The advantage of the present study is that the aforementioned empirical evidence can help decision makers to formulate effective policies to improve the efficiency. Also, effective policy tools obtained from the estimated results of influencing factors can be targeted to areas where the benefits may be greatest. That can enhance and balance development of the eastern, central, and western regions. Besides, a new grass-roots ecosystem should be established by eliminating the slack input. Innovation needs to be encouraged in the cooperative mechanism of cross regional medical services, such as the construction of a cross regional characteristic medical technology cooperation center, and building a “county medical community”. Although this study describes the spatial effect of efficiency distribution, the regression model of spatial effect needs to be further constructed to further clarify the influencing factors and degree of efficiency.

Competing Interests

The authors declare that they have no competing interests.

Contributors

All authors conceived and designed the study. LY and MX collected and curated the data, and also did the statistical analysis. All authors contributed to data interpretation. LY wrote the first draft of the Article. MX and HT interpreted the results and revised .HT critically commented on the paper. All authors approved the final version of the Article.

Data Sharing

Data are available upon reasonable request to the corresponding author.

Declaration of Interests

All other authors declare no competing interests

Acknowledgements

This study was supported by the soft science research programme from the Department of Science and Technology of Zhejiang Province (Grant NO.2021c35013) and the research project of Zhejiang University of Traditional Chinese Medicine (Grant NO.2021FSYYSY01).

Role of the Funding Source

The funders had no role in the study design, data collection, data analysis, data interpretation, writing, or interpretation of the manuscript, and the decision to submit it for publication. The corresponding author had full access to all the data in the study, and had final responsibility for the decision to submit for publication.

References

Download PDF

Citation: Liu YL, Xu RX, Meng XH, Ye YP and Xu CM. Efficiency Evaluation and Spatial Autocorrelation Analysis of Primary Health Care Resources Distribution: The Panel Three-Stage DEA Model. J Community Med Health Care. 2022; 7(1): 1057.

Home

Journal Scope

Abstract Board

Instruction for Authors

Submit Your Article