
Research Article
Austin J Comput Biol Bioinform. 2015;2(1): 1010.
Distribution of Unique Sequences in the Human Genome
Kazuharu Misawa*
Advanced Center for Computation and Communication, The Institute of Physical and Chemical Research, Japan
*Corresponding author: Kazuharu Misawa, Advanced Center for Computation and Communication, Researcher, RIKEN (The Institute of Physical and Chemical Research) Hirosawa 2-1, Wako, Saitama, 351-0198, Japan
Received: December 19, 2014; Accepted: January 20, 2015; Published: February 16, 2015
Abstract
Programmable sequence-specific endonucleases are powerful tools for genome alteration with high precision. For example, the CRISPR system is an efficient tool for genome engineering in eukaryotic cells by simply specifying a 20-bp targeting sequence within its guide RNA. When studying large genomes, however, the design of target sequences is complicated by the redundancy of sequences. The distribution of unique sequences in the genome is of interest. In this paper, I describe the development of a novel method, UF, for detecting unique 20-bp sequences in entire genomes. UF stands for "Unique Finder". By using UF, the distribution of unique sequences in the human genome was investigated. It was found that 60% of the human genome is unique on average. However, non-unique regions of human genome are concentrated on centromeres and terminal regions of the chromosomes. The proportions of unique sequences are about 80% in the rest part of the genome. The program for obtaining unique sequences is available at https://sourceforge.jp/projects/ parallelgwas/releases/
Keywords: Unique sequences; human genome; hash code; centromere; chromosome terminal region
Abbreviations
BP: Base Pairs; MB: Mega Bases1
Introduction
Targeted nucleases are useful tools for genome alteration with high precision. The RNA-guided Cas9 nuclease from the microbial Clustered Regularly Interspaced Short Palindromic Repeats (CRISPR) adaptive immune system can be used as an efficient genome engineering tool in eukaryotic cells including human cells [1]. CRISPR requires a 20-bp targeting sequence [2]. When studying large genomes, however, the design of oligonucleotides for CRISPR is complicated by the redundancy of sequences. In humans, various types of repetitive sequences account for approximately 50% of the genome [3]. Such non-unique sequences cannot be CRISPR targets, because they cause off-target reaction. In this paper, I developed a new program, UF, for detecting 20-bp sequences that are unique within a genome. To detect sequences that are unique within a genome, a new program, UF, was developed. A word is some defined number of letters. In this study, the word size set to be 20-bp. UF is based on the hash code which was used as described below. The probability of collisions to evaluate how many hash codes was estimated by using various prime numbers. By using UF, distribution of unique sequences in the human genome was investigated in this study.
Materials and Method
Overview of the algorithm of UF
The basic idea of UF is similar to the seeding algorithm of BLAST [4]. The list consists of all words (w-mers). The bases in the sequences are labelled 1, 2, 3, and 4 for T, C, A, and G, respectively. Other characters, such as N, are labelled 0. Then, an index, x, of a word can be calculated as
where ck is the label of k-th nucleotide of the word. Using this formula, instances of the word can be counted if there is sufficiently large memory. Counting the occurrences of words takes up a lot of memory. In this study, the word size, w, was set to be 20-bp. Thus, a word can be used as an index into an array of the size 520 = 95,367,431,640,625. The memory size for allocating such an array is much larger than what is available at present.
Hash table
In this paper, one hash code, h, is assigned to x by the modular arithmetic algorithm. The modular arithmetic algorithm is used for DNA pooling in an experimental study [5]. Suppose x is an index of a word and p is a prime number. Using modular arithmetics, we can obtain a hash code, h, as follows:
h = x (mod p) (2)
To count the occurrences of h, an array with its size p is required. Note that equation (2) yields the same hash code for words whose indexes are h, h + p, h + 2p, . . ., where 0 <h<p. Complementary words on the reverse strand were also analysed simultaneously. If the number of occurrences of h is 1, then the word whose index is x is unique.
Prime numbers
It must be noted that two or more distinct words have the same hash value. In computer science, this situation is called a collision. Because of collisions, having a unique hash code is a sufficient condition for being a unique word, but it is not a necessary condition. The proportion of collision is expected to be reduced by using sufficiently large number of hash codes. Prime numbers used in this study are listed in (Supplementry Table 1). These prime numbers were obtained using the method widely known as "the sieve of Eratosthenes"[6].
Chromosome
Position (MB)
Average
Location
1
122
-
123
0.07
Centromere
2
88
-
89
0.07
Centromere
5
67
-
68
0.01
Ex-centromere (?)
6
1
-
6
0.03
Terminal
8
8
-
9
0.04
Terminal
9
40
-
52
0.04
Centromere
14
1
-
2
0.07
Terminal
15
2
-
3
0.04
Terminal
17
79
-
80
0.08
Terminal
X
1
-
3
0.00
Terminal
Y
1
-
3
0.00
Terminal
Y
17
-
18
0.04
Unknown
Y
22
-
23
0.01
Terminal
Table 1: Position of non-unique regions.
Probability of collision
In this paper, the probability of collision was estimated by using the general linear regression by using the following equation:
y = a - b exp ( -cn) , (3)
Where y is the number of words whose number of occurrences of h is 1 and n is the number of prime numbers.
Output format
UF outputs unique words by using uppercase letters (T, C, A, and G) and non-unique words by using lowercase letters (t, c, a, and g). To combine the results obtained by multiple prime numbers, the letters are checked; if at least one of the letters is uppercase, the word is unique, otherwise non-unique.
Human genome
In this study, the NCBI human genome (Build 37) was analysed. The alternate loci group on chromosome 6 were excluded because the sequences of these loci were obtained from different individuals (see https://www.ncbi.nlm.nih.gov/projects/genome/assembly/ grc/human/). The human genome size is used in this study is 2,871,066,099bp.
Results
(Figure 1) shows the relationship between the number of unique words detected by UF and the number of hash codes used in the analysis. Open squares show the relationship between the number of unique words detected by UF and the number of hash codes used in the analysis. The estimates of a, b, and c in equation (3) were 2048831375, 2023511084, -0.2198, respectively. According to these estimates, probability of collision per hash code is exp (-0.2198) ≈ 0.8. These estimates also suggest 2,048,831,375 bp of human genome sequences are unique. (Figure 2) shows the proportion of unique words within the human genome detected by UF (Supplementary Table 2). Unique words were binned into a series of 1-MB windows depending on the positions of the starting point of the words. According to this figure, the proportion of unique words is about 80% in the most parts of the human genome. We can see that several regions of human genome have very low values of the proportions of unique words. Let us call the regions whose proportions of unique words are less than 0.1 as the non-unique regions.
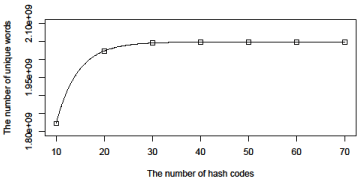
Figure 1: Relationship between the number of unique words detected by UF
and the number of hash codes used in the analysis. Open squares: Number
of unique words detected by UF. Solid line: The expected number of unique
words (see details in the main text).
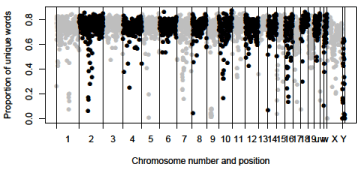
Figure 2: The number of occurrence of windows and proportion of unique
words within the genome detected by UF. Window size is 1 MB. Gray circles;
odd-numbered chromosomes and X chromosome, black circles; evennumbered
chromosomes and Y chromosome, u, v, and w; chromosome 20,
21 and 22, respectively.
(Table 1) shows the positions of the non-unique regions in the human genome. Chromosomes 1, 2, 9 have non-unique regions on centromeres. The region between 67 Mbp and 68 Mbp on chromosome 5 contains a large number of non-unique words. Chromosomes 6, 8, 14, 15, 17, X, and Y have non-unique regions on terminal regions of the chromosomes. Among these chromosomes, chromosomes 14, 15, and X are acrocentric [7].
Discussion
A new program, UF, for detecting 20-bp sequences that are unique within a genome was developed. Because the memory of computer is limited, I designed UF to map a word to a relatively small array by using a hash code. Collisions are unavoidable whenever members of a very large set are mapped to a relatively small array. The probability of hash collision for a single hash code of a 20-nucleotide word within the entire human genomewas estimated to be about 0.8. By using this estimate, we evaluated the number of hash codes to be used. To detect 90% of unique words within the human genome, 11 hash codes are required. 21 hash codes are enough for detecting 99% of unique words. In this study, 70 hash codes were used so that the proportion of undetected unique words would be less than 10-6.According to the result shown here, 2,048,831,375 bp are estimated to be unique in the human genome. Since the human genome size is used in this study is 2,871,066,099 bp, 71.36 % of human genome is estimated to be unique in this study. Li et al. [8] showed that the percentage of 20- mers that are not unique is 28.35%.The difference between the result shown here and that of Li et al. [8] is about 0.2%. This discrepancy might be due to the difference in treating undetermined "N" letters.
It is worth noting that every hash code is independent, so the calculation can be conducted in parallel. Comparing the results for all hash codes can be run concurrently for each chromosome. Thus, UF is suitable for fast detection of unique words by using PC clusters. Counting the occurrences of words in the entire genome took about 30 minutes per hash code. Comparing the occurrence of words for 70 hash codes for the largest chromosome, chromosome 1 took 30 minutes. The entire analysis took about 1 hour when I used a PC cluster that consists of 70 machines with Intel Xeon (2.93GHz). Each machine has 4 cores. Memory requirement for each machine is 4GB.
In this paper, multiple hash tables were used to find unique words from the human genome under the limitation of memory. However, if human genome was compressed, it can be kept in memory in a typical PC. Burrows-Wheeler transform[9] is one of compressing algorithms which are widely used in genome analyses. Burrows- Wheeler transform is utilized to count exact word matches [10]. Burrows-Wheeler transform is also used to obtain alignments of short reads [11] and those of long reads [12]. Compression algorithm will improve the future version of UF.
It is well known that various types of repetitive sequences account for approximately 50% of the genome [3]. This discrepancy comes from the fact that UF detects only the words that do not show perfect match to other regions, but repetitive elements consist of perfect, or slightly imperfect, copies of DNA motifs of variable lengths [13].
Different word sizes also give different results. It was observed that the proportion of non-singletons w-mers decreases slowly with increasing w[8].The distribution of unique words in various lengths must be studied in future.
A large part of non-unique regions of the human genome are centromeres and terminal regions of the chromosomes. Centromeres consist of repetitive elements known as alpha-satellite [14-16]. Previous studies show that mini satellites are mainly found in terminal regions in humans [17-20]. Human chromosome Y has unusually repetitive sequence composition [21]. These results suggest that non-unique regions consist of repetitive elements. Repetitive elements are also known to be distributed in terminal regions in human chromosomes [18,22]. According to UCSC genome browser [7], the centromeric region of chromosome 5 is around 45 Mbp to 50 Mbp, so that the non-unique region between 67 Mbp and 68 Mbp on chromosome 5 is not the centromere. Structural rearrangements of chromosome 5 have occurred along the human ancestral lineage [23]. The region might be the former centromere. Further study must be also necessary on the evolution of the repetitive elements.
UF lacks the ability of finding not-perfect matches in the genome. Since CRISPR targeting allows for ambiguity [24], UF will help to design CRISPR targets, if it allows mismatches in words.
Conclusion
A novel program, UF, for detecting 20-bp sequences that are unique in a genome was developed. UF is expected to be useful for detecting unique sequences in the genome, because it requires relatively small amount of memory but obtain the unique target sites within short time period. Non-unique regions of human genome are centromeres and terminal regions of the chromosomes. The results indicate that efficiency of 20-bp targeting sequence will be different among the positions of the genome.
Acknowledgement
The results of the calculations were performed by using the RIKEN Integrated Cluster of Clusters (RICC).
References
- Hsu PD, Scott DA, Weinstein JA, Ran FA, Konermann S, Agarwala V, et al. DNA targeting specificity of RNA-guided Cas9 nucleases. Nat Biotechnol. 2013; 31: 827-832.
- Ran FA, Hsu PD, Wright J, Agarwala V, Scott DA, Zhang F. Genome engineering using the CRISPR-Cas9 system. Nat Protoc. 2013; 8: 2281-2308.
- Treangen TJ, Salzberg SL. Repetitive DNA and next-generation sequencing: computational challenges and solutions. Nat Rev Genet. 2011; 13: 36-46.
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ. Basic local alignment search tool. J Mol Biol. 1990; 215: 403-410.
- Erlich Y. Chang K, Gordon A, Ronen R, Navon O, Rooks M, et al. DNA Sudoku--harnessing high-throughput sequencing for multiplexed specimen analysis, Genome Res, 2009; 19: 1243-1253.
- Miller GA. The So-called sieve of eratosthenes. Science. 1928; 68: 273-274.
- Bandyopadhyay R, McQuillan C, Page SL, Choo KH, Shaffer LG. Identification and characterization of satellite III subfamilies to the acrocentric chromosomes. Chromosome Res. 2001; 9: 223-233.
- Li W, Freudenberg J, Miramontes P. Diminishing return for increased Mappability with longer sequencing reads: implications of the k-mer distributions in the human genome. BMC Bioinformatics. 2014; 15: 2.
- Burrows M, Wheeler DJ. A block-sorting lossless data compression algorithm, in: Technical report, Digital Equipment Corporation, 1994.
- Healy J, Thomas EE, Schwartz JT, Wigler M. Annotating large genomes with exact word matches. Genome Res. 2003; 13: 2306-2315.
- Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009; 25: 1754-1760.
- Li H, Durbin R. Fast and accurate long-read alignment with Burrows-Wheeler transform. Bioinformatics. 2010; 26: 589-595.
- Charlesworth B, Sniegowski P, Stephan W. The evolutionary dynamics of repetitive DNA in eukaryotes. Nature. 1994; 371: 215-220.
- Murphy TD, Karpen GH. Centromeres take flight: alpha satellite and the quest for the human centromere. Cell. 1998; 93: 317-320.
- Wevrick R, Willard HF. Long-range organization of tandem arrays of alpha satellite DNA at the centromeres of human chromosomes: high-frequency array-length polymorphism and meiotic stability, Proc Natl Acad Sci U S A, 1989; 86: 9394-9398.
- Rudd MK, Wray GA, Willard HF. The evolutionary dynamics of alpha-satellite. Genome Res. 2006; 16: 88-96.
- Vergnaud G, Denoeud F. Minisatellites: mutability and genome architecture. Genome Res. 2000; 10: 899-907.
- Amarger V, Gauguier D, Yerle M, Apiou F, Pinton P, Giraudeau F, et al. Analysis of distribution in the human, pig, and rat genomes points toward a general subtelomeric origin of minisatellite structures, Genomics, 1998; 52 : 62-71.
- Ames D, Murphy N, Helentjaris T, Sun N, Chandler V. Comparative analyses of human single- and multilocus tandem repeats. Genetics. 2008; 179: 1693-1704.
- Misawa K, Minisatellites in human, mouse, cow, chicken and lizards genomes are concentrated in the terminal regions of chromosomes, submitted.
- Tilford CA, Kuroda-Kawaguchi T, Skaletsky H, Rozen S, Brown LG, Rosenberg M, et al. A physical map of the human Y chromosome. Nature. 2001; 409: 943-945.
- Bois PR. Hypermutable minisatellites, a human affair? Genomics. 2003; 81: 349-355.
- Feuk L, MacDonald JR, Tang T, Carson AR, Li M, Rao G, et al. Discovery of human inversion polymorphisms by comparative analysis of human and chimpanzee DNA sequence assemblies. PLoS Genet. 2005; 1: e56.
- Mali P, Aach J, Stranges PB, Esvelt KM, Moosburner M, Kosuri S, et al. CAS9 transcriptional activators for target specificity screening and paired nickases for cooperative genome engineering. Nat Biotechnol. 2013; 31: 833-838.