
Research Article
J Dent & Oral Disord.2017; 3(1): 1050.
Presentation of a Mathematical Model to Predict Longterm Behaviour of Implants and their Prosthesis based on Probabilistic Fatigue
Prados-Privado M1,2*, Bea JA² and Prados-Frutos JC1,2
¹Department of Medicine and Surgery, Faculty of Health Sciences, Rey Juan Carlos University, Madrid, Spain
²Applied Modelling and Instrumentation Group, Aragón Institute of Engineering Research, University of Zaragoza, Zaragoza, Spain
*Corresponding author: Prados-Privado M, Department of Medicine and Surgery, Faculty of Health Sciences, Rey Juan Carlos University, Spain
Received: January 19, 2017; Accepted: February 15, 2017; Published: February 17, 2017
Abstract
A key element for the success of a dental implant and its superstructures is related to bite forces, quality and quantity of jaw bones and implant design, among others. The goal of this study was to analyze load distribution in implantsupported dentures using probabilistic fatigue. 3D models were created employing the CAD software. An oblique load of 150 N with a 30° inclination in the linguo-buccal direction was applied. Calculations of stresses of the prosthesis and the bone were made. Then, the fatigue life (mean and variance) and the probability of failure were obtained.
Keywords: Finite element method; Probabilistic fatigue; Dental prosthesis
Introduction
A key element for the success of a dental implant and its superstructures is related to bite forces, quality and quantity of jaw bones, implant design, implant surface texture and surgical procedures [1,2]. As Li detailed in his study [3], implant diameter and implant length are well accepted as an important factor in success because they directly influence the primary stability. Clinical observations indicate that the most common cause of implant failure is incomplete osseointegration [4]. Other two potential causes of implant failure are parafunctional habits and excessive occlusal forces [5] and the passive fit and seal between the implant and its abutment components [4].
The quality of the bone varies strongly depending on the anatomic region in the mandible [3,6]. Density of bone is an essential factor in treatment planning and clinical success and it determines the surgical approach, the implant design and the healing time [7,8]. Cortical thickness tends to decrease as its moves to the posterior region of the mandible but increase its trabecular porosity. Some clinical phenomenon can be understood with a good knowledge of the bone density in different areas of the maxilla and mandible [9]. Some studies have described the close relationship between the bone density and the success of dental implants where dental implants placed in low-density areas have a higher failure rate [9,10]. According to Chugh’s study [9], the density in the maxilla and mandible increases progressively from the midline to the posterior region because of the stress distribution.
Type of loading, material and geometric characteristic of the implant, bone-implant interface and the quantity and quality of the surrounding bone have influence on the load transfer from implants to surrounding bone [1,11,12].
The use of finite element method in the analysis of implant biomechanics furnishes many advantages in the simulation of complex clinical situations. This method makes possible, from a bioengineering point of view, to design and analyze dental implants with geometry that minimize the peak bone stress [11].
The aim of the present research was to evaluate the biomechanical behavior in the bone around the implant as well as to assess the stress transfer in the implant and it superstructures using a threedimensional finite element analysis and predict the long-term behavior of the whole structure.
Material and Methods
Finite element model
3D models were created employing the CAD software Solid works 2016 [Dassault Systemes, Solid Works Corp., Concord, MA, USA]. Dental implants were provided by the manufacturer and bone geometries were created employing Solid Works.
A D2 bone type [13] was simulated and their characteristics were obtained from Vootla and coworkers [14]. Dimensions used in the bone geometry ensure avoid any undesired boundary effects shows in Figure 1. Figure 2 details the prosthesis model analyzed in this study.

Figure 1: Lingual vision of the finite element model employed in the present
study.
Figure 2: Dental prosthesis model.
Material properties
Implants and abutments were made from Ti6Al4V, as the manufactured provided. The elastic properties of the titanium alloy and bone used in the models were taken from the literature. All materials were modeled with linear, elastic, isotropic and homogeneous properties [1]. The elastic modulus and Poisson’s ratio of the titanium alloy was 100GPa and 0.3, respectively [15]. Young’s modulus and Poisson’s ratio of the bridge was 218GPa and 0.33, respectively [16]. Bone properties were taken from [17] and they are summarized in Table 1.
Material
E (GPa)
μ
Titanium
103
0.31
CrCo
218
0.33
Cortical bone
13.7
0.3
Cancellous bone
4
0.3
Table 1: Elastic properties of materials employed in the study (E: Elastic modulus, μ: Poisson’s ratio).
Boundary and loading conditions
The model was subjected to a rigid fixation restriction in the lower maxilla. An ideal osseo integrated screw implants was simulated. An oblique load of 150 N with a 30° inclination in the linguo-buccal direction was applied [18].
Probabilistic fatigue
Physical magnitudes employed in fatigue problems are usually deterministic. However, there are a lot of uncertainties that can seriously compromise the usefulness and validity of the system. Geometrical and material properties or applied loads in the structure are some of them, which are clearly justified in some problems as, dental implants.
The model proposed in this study is based on probabilistic finite element method and Markov chains [19]. The main difference between this model and other studies available in the literature is that we consider the uncertainties of the most important factors in this phenomenon and we include them in the mathematical model. Finite element analysis obtains the stress and strain distribution considering that loads and material properties do not have uncertainties. However, the probabilistic model employed in this study keeps in mind that these variables are random. The reader is referred to Prados-Privado et al. [20] for further details about the mathematical model.
Table 2 shows the force employed here obtained from [16] and the Young’s modulus and Poisson’s ratio of titanium, which have been considered as Gaussian random variables.
Force
Young’s modulus
Mean
150 N
100 GPa
Variance
10N2
20 GPa2
Table 2: Stochastic data employed.
Results and Discussion
The probabilistic model detailed here was applied to evaluate the failure probability and the mean life of prosthesis with a Neodent® implant designs under average mastication forces and ideal osseointegration.
The stress field on implants [von Mises stress] and surrounding bone [maximum principal stress] was evaluated for the case of previous static loading. Figure 3 represents the stress distribution in the whole prosthesis. The maximum principal stress distribution predicted in the cortical and trabecular bone is 9.7MPa as Figure 4 shows.
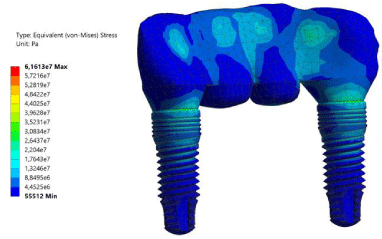
Figure 3: Von Mises stress distribution in implants and bridge.
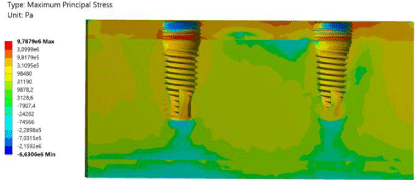
Figure 4: Maximum principal stress in bone.
The highest von Mises stress in both dental implants appears around the neck of the implants, which is in accordance with the literature.
The probabilistic methodology proposed was employed to estimate the principal statistics of the fatigue life [mean and variance] and the probability of failure of this prosthesis (Table 3).
Mean fatigue life [million cycles]
Variance fatigue life [million cycles2]
115
72
Table 3: Mean and variance of the fatigue life for the prosthesis.
The failure probability of prosthesis can be now analyzed for a specific number of loads cycles. Probability of failure associated with each cycles was obtained for the maximum von Mises stress is detailed in Figure 5.
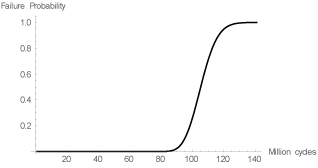
Figure 5: Dental prosthesis’ cumulative probability function.
Fracture phenomenon in dental implants is very sensitive to uncertainties in variables involved in this phenomenon but, in spite of this, most of the studies available in the literature have been done from a deterministic point of view [21,22]. The probabilistic model used in this research can help to understand the fracture mechanism in dental prosthesis because the influences of many variables are considered from the very beginning.
Conclusion
This study has applied a probabilistic methodology to an implant prosthesis with the aim of evaluate the fatigue behavior under a natural masticatory force. The current approach is based on probabilistic finite element analysis and damage model. Load transfers to a D2 bone in both dental implants have been also evaluated.
The model proposed here is useful to predict the biomechanical behavior of the prosthesis as well as the probability of failure associate without doing any mechanical test and, therefore, without breaking any implant.
Acknowledgment
The research for this paper was financially supported by the grant A274 [URJC-Neodent].
References
- Pérez MA, Prados-Frutos JC, Bea JA, Doblaré M. Stress transfer properties of different commercial dental implants: a finite element study. Comput Methods Biomech Biomed Engin. 2012; 15: 263-273.
- Dilek O, Tezulas E, Dincel M. Required minimum primary stability and torque values for immediate loading of mini dental implants: an experimental study in nonviable bovine femoral bone. Oral Surgery, Oral Med Oral Pathol Oral Radiol Endodontology. 2008; 105: 20-27.
- Li T, Hu K, Cheng L, Ding Y, Ding Y, Shao J, et al. Optimum selection of the dental implant diameter and length in the posterior mandible with poor bone quality - A 3D finite element analysis. Appl Math Model. 2011; 35: 446-456.
- Gehrke SA, Souza dos Santos Vianna M, Dedavid BA. Influence of bone insertion level of the implant on the fracture strength of different connection designs: an in vitro study. Clin Oral Investig. 2014; 18: 715-720.
- Tagger Green N, Machtei EE, Horwitz J, Peled M. Fracture of dental implants: literature review and report of a case. Implant Dent. 2002; 11: 137-143.
- Esposito M, Hirsch JM, Lekholm U, Thomsen P. Biological factors contributing to failures of osseointegrated oral implants. (I). Success criteria and epidemiology. Eur J Oral Sci. 1998; 106: 527-551.
- Premnath K, Sridevi J, Kalavathy N, Nagaranjani P, Sharmila MR. Evaluation of stress distribution in bone of different densities using different implant designs: A three-dimensional finite element analysis. J Indian Prosthodont Soc. 2013; 13: 555-559.
- Demenko V, Linetsky I, Nesvit V, Linetska L, Shevchenko A. FE study of bone quality effect on load-carrying ability of dental implants. Comput Methods Biomech Biomed Engin. 2014; 17: 1751-1761.
- Chugh T, Ganeshkar S V, Revankar A V, Jain AK. Quantitative assessment of interradicular bone density in the maxilla and mandible: implications in clinical orthodontics. Prog Orthod. 2013; 14: 38.
- Graber TM, Vanarsdall RL VK. Orthodontics: Current Principles & Techniques. Vol. 4th ed, Elsevier / Mosby. 2005; 493-542.
- Bozkaya D, Muftu S, Muftu A. Evaluation of load transfer characteristics of five different implants in compact bone at different load levels by finite elements analysis. J Prosthet Dent. 2004; 92: 523-530.
- Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: A three-dimensional finite element study. J Prosthet Dent. 2004; 91: 144-150.
- Mish E CAH. Contemporary Implant Dentistry. Mosby Elsevier. 2008. 8-13.
- Vootla NR. An Evaluation of the Stress Distribution in Screw Retained Implants of Different Crown Implant Ratios in Different Bone Densities Under Various Loads-A FEM Study. J Clin Diagno Res. 2016; 10: 96-101.
- Bidez MW, Misch CE. Force transfer in implant dentistry: basic concepts and principles. J Oral Implantol. 1992; 18: 264-274.
- Bhering CLB, Mesquita MF, Kemmoku DT, Noritomi PY, Consani RLX, Barão VAR. Comparison between all-on-four and all-on-six treatment concepts and framework material on stress distribution in atrophic maxilla: A prototyping guided 3D-FEA study. Mater Sci Eng C. 2016; 69: 715-725.
- Rubo JH, Capello Souza EA. Finite-Element Analysis of Stress on Dental Implant Prosthesis. Clin Implant Dent Relat Res. 2009; 12: 105-113.
- Almeida EO, Rocha EP, Júnior ACF, Anchieta RB, Poveda R, Gupta N, et al. Tilted and Short Implants Supporting Fixed Prosthesis in an Atrophic Maxilla: A 3D-FEA Biomechanical Evaluation. Clin Implant Dent Relat Res. 2015; 17: e332-342.
- Bogdanoff JL, Kozin F. Probabilistic models of cumulative damage. First. New York: Wiley-Interscience; 1985; 352.
- Prados-Privado M, Prados-Frutos J, Calvo-Guirado J, Bea J. A random fatigue of mechanize titanium abutment studied with Markoff chain and stochastic finite element formulation. Comput Methods Biomech Biomed Engin. 2016; 19: 1583-1591.
- Himmlová L, Dostálová T, KácovskÝ A, Konvic´ková S. Influence of implant length and diameter on stress distribution: A finite element analysis. J Prosthet Dent. 2004; 91: 20-25.
- Petrie CS, Williams JL. Comparative evaluation of implant designs: influence of diameter, length, and taper on strains in the alveolar crest. Clin Oral Implants Res. 2005; 16: 486-494.