Using a Person-Centered Methodology to Investigate the Co-Occurrence between Psychopathological Problems

Abstract

The present paper proposes that Latent Class Growth Analysis (LCGA) can be used for the identification of different groups of individuals exhibiting normative, pure or combined psychopathological problems. More specifically, LCGA allows for the identification of different subgroups of individuals who show homogeneous developmental trajectories of the behaviors under investigation, and provides the capacity for the joint estimation of trajectory models across the entire period of observation. LCGA can also aid in the identification of (1) possible factors that might place individuals at higher risk for exhibiting pure or combined psychopathology, and (2) developmental outcomes that might be related to higher risk groups of individuals. Studies using the LCGA method can offer a more comprehensive view of co-occurrence when compared to studies investigating point by point change or average trajectories of change over time. Findings on co-occurrence have the power to provide information on the validity of classification systems, etiological theories, and treatment.

Keywords: LCGA; Psychopathological problems; BIC; ANOVA

Introduction

One of the remaining major research challenges in psychology is the idea of co-occurrence [1,2]. Findings on co-occurrence are important because they can have implications for the validity of classification systems and treatment [1-5]. Furthermore, findings on factors related to co-occurrence can have implications for etiological theories, since risk factors associated with one disorder might in fact be risk factors for another disorder [2,3,6,7].

One of the main reasons behind the limited understanding of co-occurrence is the unavailability of appropriate analytic methods. Researchers have been using statistical methods, such as correlations, clinical cutoff scores, cluster analysis, and factor analysis, to identify syndromes that tend to co-occur in the individual; however these approaches are not built to take longitudinal change into account and at most these methods only test the association of two assessment periods [8]. The advent of latent growth models in Hierarchical Linear Modeling (HLM) and Structural Equation Modeling (SEM) enabled the estimation of the average trajectories of different behaviors, and the investigation of the co-development of different domains by relating their trajectories [9-12]. However, these models assume that individual curves within each behavior are relatively homogeneous and that growth trajectories in the model arise from a single multivariate normal distribution, which masks the presence of distinct subgroups.

According to Rutter and Sroufe [2], to investigate co-occurrence analytic methods need to be able to (1) take into account individual differences and possibly identify different classes of individuals exhibiting either pure or co-occurring psychopathology, (2) investigate both normative and pathological development to understand the link between them, (3) investigate the course of cooccurrence within a dynamic framework by taking trajectories of change into account, and (4) consider the origins and outcomes of cooccurrence. An analytic method that can take all of these components into account is a person oriented methodology known as Latent Class Growth Analysis [7,13], which is similar to the semi parametric group based trajectory approach proposed by Nagin [14].

LCGA allows for the identification of different subgroups of individuals who show homogeneous developmental trajectories of the target behavior [7,15,16]. Furthermore, the LCGA approach can relate the entire longitudinal course of two or more behaviors, and therefore provides the capacity for the joint estimation of trajectory models across the entire period of observation [7,8.13]. Hence, LCGA first identifies heterogeneous classes within each behavior of interest based on individuals’ distinct developmental courses and then joins these differential trajectories to determine which groups of individuals follow trajectories of normative, pure, or co-occurring psychopathological problems. After the identification of the different latent classes, possible factors that might place individuals at higher risk for exhibiting pure or combined psychopathological problems, and possible developmental outcomes that might be related to psychopathology can be included in the analyses [7].

Studies using the LCGA method can offer a more comprehensive view of co-occurrence when compared to studies investigating point by point change or average trajectories of change over time. LCGA enables the identification of heterogeneous developmental patterns of pure or combined psychopathological problems within a dynamic framework by taking trajectories of change into account, by investigating non-linear change, and by including all the available longitudinal data (even incomplete data) in the analysis. Additionally, while latent growth models assume that individual curves within each behavior are relatively homogeneous and that growth trajectories in the model arise from a single multivariate normal distribution, LCGA enables researchers to identify heterogeneous trajectories representing latent classes of individuals by modeling a mixture of distinct multivariate normal distributions [7,8,13,17]. Furthermore, based on the heterogeneous trajectories of each latent class and by taking longitudinal change into account, LCGA also estimates the joint occurrence among distinct latent classes of different behaviors, while latent growth models investigate the co-development of the average trajectories of change for each behavior. Finally, predictors and outcomes can be added in the analysis to compare groups of individuals exhibiting continues normative, pure, and co-occurring psychopathological problems.

Employing LCGA for the Investigation of Co-Occurrence

The next part of the paper aims to provide a description of how to use LCGA to investigate co-occurrence using the Mplus software [7,15]. In the first stage of the analyses, a single-latent growth model can be used to identify the average trajectories of psychopathological problems. In the second part of the analyses, LCGA can be used to identify distinct groups of individual trajectories separately for each problem behavior. The joint probabilities can be derived from a mixture model which includes the individual trajectories derived from the LCGA analysis. In the final stage, predictors and outcomes can be added in the analyses to identify characteristics that distinguish membership in the identified groups.

Average trajectories of psychopathological problems

A single-class latent growth model can be used to investigate the normative development of psychopathological problems. This type of growth model uses a polynomial function to model the relationship between the behavior under investigation and age [7,18]. The function takes the form

y_ιt= βo + β1Age_ιt + β₂Age²_ιt + ε (1.1)

where y_ιt is a latent variable which characterizes the level of psychopathological problems for participant ι at time t. As seen in equation 1.1, the analysis is based on a quadratic growth curve. Investigators can decide which growth terms to include in their analysis based on the available times of measurement in their study. For example, if only three time points of measurement are available, only the intercept and the linear slope should be included in the equation. The unit of time in the equation is years of age; however grade or time of measurement can also be used as alternatives. Age_ιt is participant ι’s age at time t, Age² _ιtis the square of participant ι’s age at time t, and ε is a disturbance assumed to be normally distributed. The model’s coefficients, β_o, β₁, and β₂, determine the average shape of the trajectory. The single class growth analysis is demonstrated in Digure 1, with Time of measurement as the unit of analysis. The intercept indicates the average of each problem behavior at Time 1, and the linear and quadratic terms represent change over time.

Patterns of psychopathological problems over time

LCGA identifies heterogeneous classes by modeling a mixture of distinct multivariate normal distributions. Heterogeneity of trajectory classes is data-driven based on the estimation of individual growth curves for each participant. Individuals within each class are assumed to be homogeneous in respect to their developmental patterns. LCGA uses a polynomial function to model the relationship between an attribute and age [14,16,18,19]. The function takes the form [7,14]:

y_ιt^j = β^j_o + β^j₁Age_ιt + β^j₂Age²_ιt + e (1.2)

where y_ιt^jis a latent variable which characterizes the level of psychopathological problems for participant _ιt at time t given membership in group j. Age_ιt is participant _ιt’s age at time t, Age2 _ιt is the square of participant _ιt’s age at time t, and e is a disturbance assumed to be normally distributed with zero mean and constant variance. The model’s coefficients, β^{j o}, β^{j 1}, and β^{j 2}, determine the shape of the trajectory. The coefficients are superscripted by j to denote that they are not constrained to be the same across j groups and are free to vary, which allows for cross-group differences in the shape of developmental trajectories. Therefore, the absence of constraints captures mixtures of developmental trajectories in the population and also allows each group’s trajectory to have a distinct shape. Furthermore, the model does not permit individual variability in the intercepts or slopes within classes, and individuals within a class share a single trajectory of change over time. The LCGA model estimation in Mplus results in three outputs: (1) the shape of the trajectory for each class, (2) the un standardized and standardized values of each growth term for each class of individuals, and (3) the posterior probability of class membership. In addition, Mplus accommodates missing data by using full information maximum likelihood, retaining children with incomplete assessments in the analysis.

Model fit

The Lo, Mendel, Rubin (LMR) statistic and the Bayesian Information Criterion (BIC) can be used to compare models with different number of classes. Both of these model fit statistics should be used because they provide information about different aspects of model fit. The LMR statistic complements the BIC because the BIC tends to favor more parsimonious models compared to the LMR [19].

The BIC is usually used for LCGA models because it can be applied to nonnested models. The BIC, like all information criterion indices, is a goodness-of-fit measure that incorporates various penalties for model complexity, such as the number of parameters in the model [20-22]. The BIC is based on a maximization of a log likelihood function. If L is the maximized log likelihood, p is the number of free parameters in the model, and N is the number of cases, the BIC can be written as follows [22]:

BIC = -2 logL + p log(N), (2.1)

with a smaller value indicating a better fit [7]. The BIC does a good job in identifying the true model in large samples, but the BIC is biased in small samples by choosing models that are too simple [23].

In addition, because the BIC criterion tends to favor models with fewer classes by penalizing for the number of parameters [24], a likelihood statistic based on the sum of chi-square distributions should also be used. However, the usual likelihood ratio chi-square difference test can only be applied to compare nested models with the same number of classes, and therefore this type of test cannot be applied to mixture modeling with different number of classes [25,26]. Lo, Mendell, and Rubin adjusted the likelihood ratio test in order to be used in mixture modeling, to compare models with different number of classes, and to enable the comparison of non-nested models. Therefore, the Lo, Mendel, Rubin (LMR) fit statistic can be used to compare mixture models with different number of latent classes [25,26]. The LMR statistic tests k – 1 class against k classes, and it can be considered as a likelihood ratio test between models with different number of latent classes. A significant chi-square value (p < .05) indicates that the k – 1 class model has to be rejected in favor of the k-class model. A non-significant chi-square value (p > .05) suggests that a model with one fewer class is preferred. For example, in the case where 2- and 3-class models are compared, the null hypothesis states that a random sample was drawn from a mixture distribution with two classes, and the alternative hypothesis states that the sample has been drawn from a mixture distribution with 3-classes.

Furthermore, attention should be given to the shape and location of the different estimated class trajectories to indicate whether each latent class is distinct and whether the latent classes identified are meaningful. Nagin and Tremblay [8] indicated that the addition of a new class to the model might result in the splitting of a larger class into two smaller classes with similar trajectories, which is not informative. Therefore, when inspection of the graphs suggests that a model with more classes indicates the existence of similar classes of small theoretical importance, the model with fewer and distinct classes should be preferred.

Finally, the average posterior probabilities and the entropy value can be taken under consideration to indicate whether the classes in the final model are distinct [27]. Posterior probabilities determine the most likely latent class for each individual. The average posterior probabilities can be used to check for the precision of classification for each class of individuals, and therefore indicate the degree to which the classes are distinguishable. Average probabilities equal to or greater than .70 imply satisfactory fit [7,28]. In addition, the entropy value, which is a standardized summary measure based on the posterior class membership probabilities derived from each model, can be used to judge the classification accuracy of placing participants into classes and the degree of separation between classes [13,29]. Entropy can be represented as follows [29]:

E_K = 1 –(S_i S_K –p_iK lnp_iK) / n lnk (2.2)

where p^ik is the estimated conditional probability for individual i in class k, and n is the sample size. Entropy can range from zero to one, and a higher entropy value is preferred because it indicates clear classification and greater power to predict class membership. Moreover, entropy is a function of the number of classes, which suggest that a model with as many classes as observations would have an entropy value of one.

Joint probabilities

In the third part of the analysis, the groups identified with LCGA need to be entered in a joint mixture model in Mplus to investigate for joint probabilities between the two (or more) types of problem behaviors [7,13]. The joint analysis is based on the same principles as LCGA and assigns class membership in trajectory classes across behaviors taking into account longitudinal change over time. The inclusion of individuals in different combined classes is datadriven based on the estimation of individual growth curves for each participant. After identifying the latent classes based on the growth parameters for each problem behavior, the same growth terms should be used to combine the different classes and assign each individual in either a normative group, a co-occurring group or a group characterized as higher in one behavior and lower in the other [7,13]. For example, to specify a high risk co-occurring group, the intercept, linear and quadratic terms from the high risk group in one psychopathological problem, and the intercept, linear and quadratic terms from the high risk group in the other psychopathological problem should be combined to specify one joint class. The individuals who are at high risk on both psychopathological problems will be identified in the high co-occurring class. This procedure should be done for all the identified classes of each psychological problem. The Mplus guide provides a detailed explanation on how to write the syntax [15]. Figure 1 demonstrates how this approach works. As shown in the figure, this model uses all longitudinal measurements and links the two behaviors of interest across the entire period of observation. Furthermore, this type of procedure is preferred over simple crosstab analysis because it provides posterior probabilities and a value for entropy [8,13], which can be used to indicate whether the classes in the final model are distinct. Furthermore, the latent variables derived from LCGA have the potential to reduce measurement errors. The identified joint trajectories can be graphically displayed; representing distinct co-occurring groups [7].

    

    

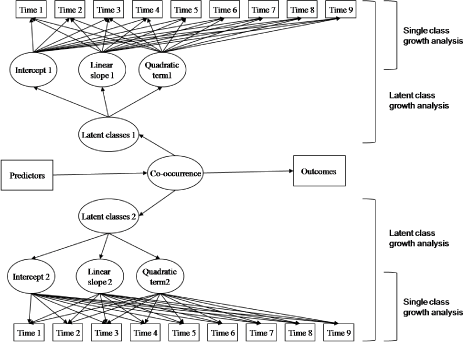
    Figure 1:  Schematic depiction of the joint Latent Class Growth Analysis model.