Jung C; Schindler D

Research Article

Austin J Earth Sci. 2015;2(1): 1006.

Statistical Modeling of Near-surface Wind Speed: A Case Study from Baden-Wuerttemberg (Southwest Germany)

Jung C and Schindler D*

Chair of Meteorology and Climatology, Albert-Ludwigs-University of Freiburg, Germany

*Corresponding author: : Schindler D, Chair of Meteorology and Climatology, Albert-Ludwigs-University of Freiburg, Werthmannstrasse 10, D-79085 Freiburg, Germany

Received: December 15, 2014; Accepted: January 29, 2015; Published: January 31, 2015

Abstract

In this paper a methodology is presented that can be used to statistically model characteristics of near-surface wind speed in complex terrain at high spatial resolution. It was developed based on daily mean wind speed time series provided by the German Weather Service for 65 stations located in southwest Germany. After comprehensive preparation of the wind speed data that were measured in the period 1975 to 2010 including gap filling, homogenization, detrending and measurement height correction, 48 continuous distributions were fitted to the empirical distributions associated with the wind speed time series. The results of the evaluation of the goodness-of-fit demonstrate that the five-parameter Wakeby-distribution characterizes the statistical properties of measured wind speed better than all other tested distributions. Based on surface roughness, terrain-related parameters (curvature, topographic exposure) and ERA-Interim reanalysis wind speed data available for the 850 hPa pressure level, LSBoost-models were built to estimate station-specific Wakeby-parameters. The LSBoost-models were then used to model the Wakeby-parameters on a 50 m resolution grid in the entire study area as a function of the predictor variables. The area-wide availability of the Wakeby-parameters allows producing detailed wind speed quantile maps.

Keywords: Wind speed measurement; Ensemble methods; Wakebydistribution; Hellmann power law

Introduction

A measure often used to quantify characteristics of near-surface wind fields is the absolute value of the horizontal wind vector commonly known as wind speed. While variations of wind speed at the earth surface are ubiquitous, there is often limited knowledge about the wind speed characteristics at a particular site. An inherent characteristic of wind speed is its high spatiotemporal variability [1,2]. Especially rough surfaces [3] and complex terrain [4] modify nearsurface wind fields. Unfortunately, there are often too few wind speed measuring stations in place although wind speed measurements made near the ground are strongly influenced by land cover and terrain at and around the measuring sites [5-7]. The lack of near-surface wind speed measurements often limits knowledge about statistical wind speed properties and thus about the local wind resource. the basis for the selection of most appropriate sites for wind turbines which offer great potential to reduce CO₂-emissions [18].

There is ongoing debate whether there is a distribution function that describes empirical distributions of wind speed data best [19,20]. In many previous studies [1,2,4,6,19-29], the Weibull function was used to represent empirical wind speed distributions. However, results from other studies [30-33] demonstrate that wind speed distributions cannot always adequately be represented by the Weibull distribution, especially when wind speed strongly varies with wind direction [34].

Since the orography in the southwest of Germany is complex and the landscape is compartmentalized, the near-surface wind speed characteristics vary on small scales, i.e. from measuring station to measuring station. Thus, the goals of this study are (i) to evaluate which distribution function is most appropriate for describing the statistical properties of wind speed data measured near the ground in the southwestern German federal state Baden-Wuerttemberg, (ii) to develop a statistical model based on the best-fitting distribution that is able to provide reasonable estimates of near-surface wind speed quantiles in high spatial resolution (50 m resolution grid) in the study area.

Material and Methods

Study area

The study area is the German federal state of Baden-Wuerttemberg (southwest Germany). It has a surface area of 35752 km². Its orography is complex and includes the low mountain ranges Black Forest (length ~150 km, width ~30-50 km, highest elevations > 1400 m) and Swabian Alb (length ~180 km, width ~35 km, highest elevations > 1000 m) as well as the broad, flat Rhine Valley, which borders on France in the west. The elevation (Φ) within the study area ranges from 85 m above sea level (a.s.l.) in the Rhine Valley to 1493 m a.s.l. at the top of the Feldberg, which is the highest mountain in Baden- Wuerttemberg. The Φ-values in the study area mainly vary between 200 m and 800 m a.s.l. (Figure 1a). The land cover types within the study area might change on small scales (< 1 km) and often create a compartmentalized landscape. The land cover types available from the Corine Land Cover (CLC) 2006 dataset for Germany [35] and the roughness length (z₀) values associated with these land cover types are listed in Table 1. Rough surface types like urban areas and forests have higher z₀-values (1.00 m and 0.80 m) than smoother surface types like agricultural areas (0.10 m) or natural grass land (0.03 m). The z₀- values, which were interpolated from the original spatial resolution of the CLC-dataset of 100 m to a 50 m resolution grid, correspond to standard z₀-values found in literature [36-38]. According to the CLCdata, the study area’s surface is mainly covered by agricultural areas (51%), forests (38%) and artificial surfaces like urban areas, airports, road networks and rail networks (9%). The corresponding bimodal z₀-value distribution is displayed in Figure 1b.

Table 1: Land cover types available from the Corine Land Cover 2006 dataset for Germany [35] and corresponding roughness length (z₀) values.




  
    ID 
    Land cover type 
    z₀ (m) 
  
  
    1 
    Urban area
    1.000
  
  
    2 
    Forested area
    0.800
  
  
    3 
    Green urban area
    0.500
  
  
    4 
    Agricultural area
    0.100
  
  
    5 
    Natural grass land
    0.030
  
  
    6 
    Airports
    0.010
  
  
    7 
    Open spaces with little vegetation
    0.010
  
  
    8 
    Water bodies
    0.005



Table 1:  Land cover types available from the Corine Land Cover 2006 dataset for
Germany [35] and corresponding roughness length (z₀) values.

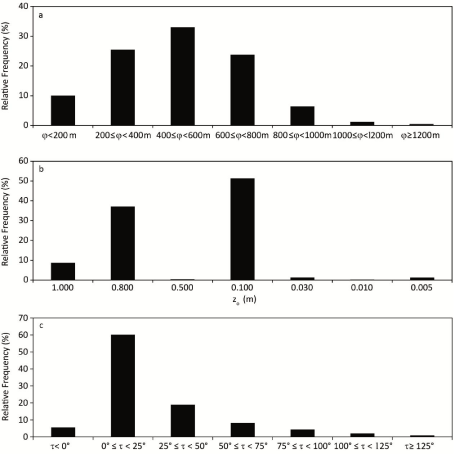
Figure 1: Relative frequency histograms illustrating the distributions of (a) elevation (Φ) values, (b) roughness length (z₀) values and (c) topographic exposure score (τ) values occurring in the study area.

    
    
    Figure 1:  Relative frequency histograms illustrating the distributions of (a)
elevation (Φ) values, (b) roughness length (z₀) values and (c) topographic
exposure score (τ) values occurring in the study area.

The complexity of the terrain in the study area was further quantified by a distance limited topographic exposure score (τ) which was described by [39,40]. The τ-values were calculated by summing the vertical angles to the skyline at 100 m intervals for the eight main compass directions up to a distance limited to 1000 m for each grid cell. Lower τ-values indicate higher exposition of a site to wind. In the study area, close to 60% of all τ-values are in the range 0^O to 25^O (Figure 1c). The τ-values used in this study were pprovided by the Forest Research Institute of Baden-Wuerttemberg.

Wind speed data

Daily mean wind speed values provided by the German Weather Service (DWD) for 65 meteorological stations were used in the present study. The stations are listed and indexed in Table 2. The indexed DWD-stations are distributed in the entire study area as well as in the bordering federal states Rhineland-Palatinate, Hesse and Bavaria as shown in Figure 2. Although hourly mean wind speed values are also available from the DWD, daily mean wind speed values available for the period 1975-01-01 to 2010-12-31 were used here (i) to maximize the number of stations with multi-year wind speed records and (ii) to minimize the effects of terrain-induced wind speed variations on sub-daily scales. Wind speed data measured at sub-daily intervals might introduce local, diurnal and multi-modal behavior into time series [30,41-43] that is often not reflected by neighboring stations, especially in complex terrain. The potential to fill data gaps in multimodal, but mostly incomplete wind speed time series using wind speed data from neighboring DWD-stations is limited. Moreover, it is important to note that until 2001-03-31 daily mean wind speed values provided by the DWD were calculated from three measurements made at the climatological standard times (7 a.m., 2 p.m. and 9 p.m.). Afterwards, 24 hourly mean wind speed values were used to calculate daily mean values.

Table 2: List of indexed DWD-stations: stations with ID-values 1-51 are included in the parameterization data set (DS1); stations with ID-values 101-114 are included in the validation data set (DS2).




  
    ID 
    Station 
    ID 
    Station 
  
  
    1
    Albstadt-Onstmettigen
    34
    Münstertal
  
  
    2
    Bad Herrenalb
    35
    Öhringen
  
  
    3
    Bad Säckingen
    36
    Pferdsfeld
  
  
    4
    Bad Wildbad-Sommerberg
    37
    Schluchsee
  
  
    5
    Baiersbronn-Obertal
    38
    Schömberg
  
  
    6
    Beerfelden
    39
    Schwäbisch Gmünd
  
  
    7
    Dobel
    40
    Stimpfach-Weiptershofen
  
  
    8
    Donaueschingen
    41
    Stötten
  
  
    9
    Dörrmoschel-Felsberghof
    42
    Stuttgart Schnarrenberg
  
  
    10
    Enzklösterle
    43
    Stuttgart-Echterdingen
  
  
    11
    Eschbach
    44
    Titisee
  
  
    12
    Feldberg
    45
    Triberg
  
  
    13
    Freiburg
    46
    Uffenheim
  
  
    14
    Freudenstadt
    47
    Ulm
  
  
    15
    Friedrichshafen
    48
    Ulm-Wilhelmsburg
  
  
    16
    Gailingen
    49
    Waldachtal-Lützenhardt
  
  
    17
    Hinterzarten
    50
    Walldürn
  
  
    18
    Höchenschwand
    51
    Würzburg
  
  
    19
    Hornisgrinde
    101
    Bad Dürrheim
  
  
    20
    Idar-Oberstein
    102
    Dogern
  
  
    21
    Isny
    103
    Lindau
  
  
    22
    Kandern-Gupf
    104
    Müllheim
  
  
    23
    Karlsruhe
    105
    Neuhausen ob Eck
  
  
    24
    Kempten
    106
    Pforzheim-Ispringen
  
  
    25
    Klippeneck
    107
    Sipplingen
  
  
    26
    Königsfeld
    108
    Söllingen
  
  
    27
    Konstanz
    109
    Stockach-Espasingen
  
  
    28
    Lahr
    110
    Stuttgart-Stadt
  
  
    29
    Laupheim
    111
    Todtmoos
  
  
    30
    Leipheim
    112
    Waldsee, Bad-Reute
  
  
    31
    Mannheim
    113
    Weilheim-Bierbronnen
  
  
    32
    Memmingen
    114
    Weingarten
  
  
    33
    Michelstadt Vielbrunn



Table 2:  List of indexed DWD-stations: stations with ID-values 1-51 are included
in the parameterization data set (DS1); stations with ID-values 101-114 are
included in the validation data set (DS2).

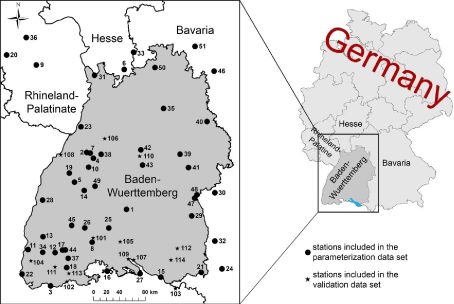
Figure 2: The study area Baden-Wuerttemberg in the southwest of Germany and the locations of the 65 wind speed measuring stations.

    
    
    Figure 2:  The study area Baden-Wuerttemberg in the southwest of Germany
and the locations of the 65 wind speed measuring stations.

Wind direction was not included in model development because of (i) the limited number of wind direction measurements in the study area and (ii) the complexity of the terrain in the study area which induces a spatiotemporal variability in wind direction that cannot be reproduced by the available measuring stations.

Out of the 65 wind speed time series 51 time series are combined in the parameterization dataset (DS1). This dataset was used for model building and parameterization. 15 DS1-time series, for which wind speed data are available for more than 85% of all days in the investigation period, served as reference time series (DS1_ref). The DS1_ref-data subset was used to complete and prepare all other wind speed time series. Wind speed values measured at 14 DWD-stations were combined to the validation dataset (DS2) and used to validate the model developed based on the data contained in DS1.

In the investigation period, wind speed (U_meas) was not always measured at the standard measurement height of 10 m above ground level (a.g.l.) defined by the World Meteorological Organization (WMO). Moreover, at a number of stations the measurement height changed within the investigation period. In these cases, the measurement height at which wind speed was measured at the end of the investigation period was defined as “representative” (h_repr) for the respective station.

In Figure 3 important characteristics of the measurement sites are summarized as boxplots. The stations are located in the Φ-range 96 m to 1481 m a.s.l. (Figure 3a) with the Φ-median being 475 m. Two stations (Feldberg, Hornisgrinde) are located above 1100 m. The hrepr-median is 10 m a.g.l. (Figure 3b). However, at a few sites, wind speed measurements have been carried out far off the WMO-standard, e.g. 3 m a.g.l. at the stations Dobel and Isny or 48 m a.g.l. at the station Karlsruhe.

Figure 3: Boxplots illustrating characteristics of the measuring stations and corresponding wind speed time series: (a) elevation (Φ), (b) representative measurement height (h_repr), (c) data availability (DA), (d) mean wind speed

{\bar{U}}_{m e a s}

(e) wind speed variance σ², (f) median wind speed

{\tilde{U}}_{m e a s}

, (g) skewness (v) of U_meas, (h) kurtosis (w) of U_meas.

    
    
    Figure 3: Boxplots illustrating characteristics of the measuring stations and corresponding wind speed time series: (a) elevation (Φ), (b) representative measurement height (h_repr), (c) data availability (DA), (d) mean wind speed  ${\bar{U}}_{m e a s}$ 
 (e) wind speed variance σ², (f) median wind speed  ${\tilde{U}}_{m e a s}$ 
, (g) skewness
(v) of U_meas, (h) kurtosis (w) of U_meas.

None of the analyzed wind speed time series was complete. Data availability (DA) ranges between 13% corresponding to about 4 years and 8 month (station Hornisgrinde) and 99.7% (Figure 3c). The median of station-specific mean values of U_meas ( ${\bar{U}}_{m e a s}$ ) is 2.5 m/s (Figure 3d) and the associated median of the variance of ${\bar{U}}_{m e a s} (σ2) displayed in Figure 3e is 1.5 (m/s)2. Since wind speed values are non-normally distributed, the station-specific medians of U$ _meas ( ${\tilde{U}}_{m e a s}$ ) are presented in Figure 3f in addition to Ū_meas . The median of ${\bar{U}}_{m e a s}$ ~ is slightly lower (2.2 m/s) than the median of meas Ū . The medians of skewness (v) and kurtosis (w) of Umeas are 1.5 (Figure 3g) and 3.0 (Figure 3h). The shape of the v-boxplot indicates that all empirical wind speed distributions are right-skewed which is supported by the meas U ~ -values being mostly lower than the Ū_meas -values. The w-boxplot indicates that all empirical wind speed distributions are more peaked than the normal distribution.

Data preparation

Since time series of wind speed measured near the ground are known to have problems with temporal homogeneity, spatial representativity and completeness, a comprehensive data preparation process preceded the statistical analysis and model building. Inhomogeneities and temporal discontinuities in wind speed time series can arise from station relocation [44,45], instrument change [44], changes in measurement height [44-47], changes in sampling frequency [45] and changes in the surroundings of the measurement sites [5,45,48]. It is critical that all wind speed data are consistent before analysis. Especially, adjusting the actual measurement height to a common height is of great importance [44,46,47].

Data preparation started with completing the 15 wind speed time series contained in DS1_ref by using the ensemble learning method bagging implemented in the Matlab^® Statistics Toolbox (The Math Works Inc., Natick, MA, Release 2014a). Bagging stands for bootstrap aggregating and enhances the predictive capabilities of machine learning algorithms used in regression [49,50].

Before gap filling started, it was made sure that the Bagging models are able to reproduce the data of the incomplete time series with high accuracy. The coefficient of determination (R²) which was calculated between the available measured data and the modeled parts of the incomplete time series was always higher than 0.90 during the gap filling process. Up to six wind speed time series measured at neighboring DWD-stations were used to mutually fill gaps in DS1_ref -time series.

Following gap filling, the completed DS1_ref -time series were tested for homogeneity. The search for inhomogeneities started with the analysis of the DWD-metadata describing station history. Unfortunately, the documentation of station history was often poor and only of limited use because the metadata provide only basic information on data quality, station relocations and changes in measurement height.

In a second step, inhomogeneities were searched and identified by using the RHtestsV4 software package implemented in R [51] by [52]. The methodology is based on the penalized-maximal-F-test [53,54] and quantile-matching [55]. The penalized-maximal-F-test is used to control whether there are shifts in the trend component during the measurement period, while considering annual cycle, linear trend and lag-1 autocorrelation. After the detection of shifts in the trend component, quantile-matching adjusts the empirical distributions of all inhomogeneous time series segments to the empirical distribution of the last homogeneous time series segment.

After completing the DS1_ref -data homogenization process, the linear trend was removed from the wind speed time series because the proposed statistical model does not consider the trend component. The 15 completed, homogenized and detrended DS1_ref -time series were then used to fill the gaps in all other 50 wind speed time series with DA < 85%. Bagging was applied again to fill the data gaps by using up to six DS1_ref -time series. Then the completed time series were tested for homogeneity and detrended as described above.

The Hellmann power law [56] was used to extrapolate wind speed to the WMO-standard wind speed measurement height of 10 m a.g.l. at all stations where necessary. Since the application of the Hellmann power law requires wind speed data from a second height a.g.l., use was made of the area-wide available ERA-Interim reanalysis wind data [57] provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). The reanalysis data is interpreted as an indicator of the kinetic energy resource available from higher parts of the troposphere that has a determining influence on the near-surface wind speed field.

In the study area, the reanalysis data have a spatial resolution of 0.125^O (~13 km). After pre-testing the predictive power of the two horizontal ERA-Interim wind vector components (u, v) available at the 700 hPa, 850 hPa and 950 hPa pressure levels, which are affected only to a limited extent by surface properties, it turned out that the 850 hPa level horizontal wind vector component data (u_850hPa, v_850hPa) were the most informative predictors for the target variables modeled in this study. Thus, u_850hPa- und v_850hPa-values available for 00 UTC, 06 UTC, 12 UTC and 18 UTC in the period 1979-01-01 to 2010-12-31 were used to calculate daily mean values of wind speed (U_850hPa). As done by [58], the absolute height a.g.l. associated with daily U_850hPa- values was derived from the ERA-Interim geopotential height layer by converting geopotential height (gpdm) to geometric height (h_850hPa) in meters a.g.l. In order to make the U_850hPa -data usable as predictor variable for the final wind speed model, it was interpolated on a 50 m resolution grid. It was shown by [59] that U_850hPa changes only little on scales comparable to the size of the study area, so the interpolation was thought of being justified.

Based on daily Umeas- and U850hPa -values at the nearest ERAInterim grid points to the positions of the 65 DWD-stations, the median value of the Hellmann exponent ) E ~ ( was calculated for all stations. The equation used to calculate $\tilde{E}$ is:

$\tilde{E} = \frac{\ln (U_{850 h P a} / U_{m e a s})}{\ln {(h_{850 h P a} / h_{r e p r})}^{^{}}}$ (1)

Once station-specific $\tilde{E}$ is known, it can be used to calculate daily, station-specific U_10m -values:

$U_{10 m} = U_{m e a s} \cdot {(\frac{10 m}{h_{r e p r}})}^{\tilde{E}}$ (2)

The values of $U_{10 m} = U_{m e a s} \cdot {(\frac{10 m}{h_{r e p r}})}^{\tilde{E}}$ determined for the 65 stations ranged between 0.06 (station Hornisgrinde) and 0.66 (station Triberg). At all grid points in the study area, $U_{10 m} = U_{m e a s} \cdot {(\frac{10 m}{h_{r e p r}})}^{\tilde{E}}$ varies between 0.06 and 0.70.

Effects of atmospheric stability on the Hellmann power law [47] were not considered because the data that is needed to adequately take atmospheric stability into account were not available.

Probability distribution fitting

To provide probabilistic estimates of the long-term spatial variability of the near-surface wind speed pattern in the study area, 48 cumulative distribution functions (CDF) were fitted to the empirical cumulative distribution functions (CDF_emp) derived from the wind speed time series. The EasyFit software (MathWave Technologies, Dnepropetrovsk, Ukraine, version 5.5) was used to carry out the estimation of CDF-parameters as well as to calculate CDF and evaluate the goodness-of-fit. Basic information on the fitted distributions, the number of CDF-parameters and the fitting methods implemented in the EasyFit software are summarized in Table 3 according to [60]. Depending on the distribution, the EasyFit software applies maximum likelihood estimation (MLE), least square estimation (LSE), method of moments (MOM) and method of L-moments (LMOM) to fit CDF to CDF_emp.

Table 3: Distributions with abbreviation (number of distribution parameters) and method used by the EasyFit software to fit CDF to CD_Femp [60].




  
    Distribution 
    Abbreviation

      (no. parameters), fitting method 
    Distribution 
    Abbreviation

      (no. parameters),

      fitting method 
  
  
    Beta
    BE4, MLE
    Laplace
    LA2, MOM
  
  
    Burr
    BU3, MLE
    Levy
    LE1, MLE
  
  
    BU4, MLE
    LE2, MLE
  
  
    Cauchy
    CA2, MLE
    Log-Gamma
    LG2, MOM
  
  
    Chi-Squared
    CH1, MOM
    Logistic
    LO2, MOM
  
  
    CH2, MLE
    Log-Logistic
    LL2, LSE
  
  
    Dagum
    DA3, MLE
    LL3, MLE
  
  
    DA4, MLE
    Lognormal
    LN2, MLE
  
  
    Erlang
    EL2, MOM
    LN3, MLE
  
  
    EL3, MLE
    Log-Pearson
    LP3, MOM
  
  
    Error
    ER3, MLE
    Nakagami
    NA2, MOM
  
  
    Error Function
    EF1, MOM
    Normal
    NO2, MLE
  
  
    Exponential
    EX1, MOM
    Pareto (1^st kind)
    PAF2, MLE
  
  
    EX2, MLE
    Pareto (2^nd kind)
    PAS2, MLE
  
  
    Fatigue Life
    FL2, MLE
    Pearson Type 5
    PFi2, MLE
  
  
    FL3, MLE
    PFi3, MLE
  
  
    Frechet
    FR2, LSE
    Pearson Type 6
    PSi3, MLE
  
  
    FR3, MLE
    PSi4, MLE
  
  
    Gamma
    GA2, MOM
    Pert
    PE3, MLE
  
  
    GA3, MLE
    Phased Bi-Exponential
    PBE4, LSE
  
  
    GeneralizedExtreme Value
    GE3, LMOM
    Phased Bi-Weibull
    PBW6, LSE
  
  
    GeneralizedGamma
    GG3, MLE
    Power Function
    PF3, MLE
  
  
    GG4, MLE
    Rayleigh
    RA1, MOM
  
  
    Generalized Logistic
    GL3, LMOM
    RA2, MLE
  
  
    Generalized Pareto
    GP3, LMOM
    Reciprocal
    RE2, MLE
  
  
    Gumbel Max
    GMX2, MOM
    Rice
    RI2, MLE
  
  
    Gumbel Min
    GMN2, MOM
    Student's t
    ST1, MOM
  
  
    HyperbolicSecant
    HS2, MOM
    Triangular
    TR3, MLE
  
  
    Inverse Gauss
    IG2, MOM
    Uniform
    UN2, MOM
  
  
    IG3, MLE
    Wakeby
    WK5, LMOM
  
  
    Johnson SB
    JSB4, MOM
    Weibull
    WE2, LSE
  
  
    Johnson SU
    JSU4, MOM
    WE3, MLE
  
  
    Kumaraswamy
    KU4, MLE



Table 3:  Distributions with abbreviation (number of distribution parameters) and method used by the EasyFit software to fit CDF to CD_Femp [60].

For each of the 65 stations the goodness-of-fit of the 48 CDF was evaluated by (i) applying the Kolmogorov-Smirnov (KS) Test [24,34,61,62] and (ii) analyzing probability-probability (P-P) plots which plot CDF and CDF_emp against each other [20,63]. The decision to use the KS-Test for goodness-of-fit evaluation was made because the KS-Test weights central tendencies more than other commonly used goodness-of-fit tests like the Anderson-Darling test [64]. The Anderson-Darling test weights observations in the distribution tails more than the KS-Test.

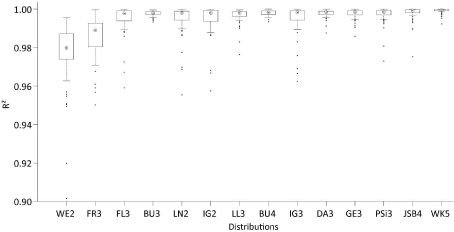
As will be demonstrated in the Results and Discussion section, the five-parameter Wakeby-distribution [65] shows a better performance than all other distributions. The Wakeby-distribution (WK5) is therefore chosen to model statistical properties of the empirical wind speed distributions. The Wakeby-distribution can be defined by its quantile function as [66-70]:

$x (F) = ε + \frac{α}{β} [1 - (1 - F) ^{β}] - \frac{γ}{δ} [1 - {(1 - F)}^{- δ}]$ (3)

where F is the non-exceedance probability with x(F) being the F-associated quantile value, α, β, γ and δ are parameters and ε is the location parameter. This parameterization exhibits WK5 being a generalization of the Generalized Pareto distribution for α = 0 or γ=0. To be a valid quantile function the conditions γ = 0 and α + γ = 0 must hold. The quantile function is defined for the domain ε = x < ∞ if δ = 0 and γ > 0, ε = x = e + α/β - γ/δ if δ < 0 and γ = 0 [67-69].

Geographic data

For WK5-model building, the predictive power of the predictor variables listed in Table 4 was tested. In addition to Φ, the orographic features aspect (η), curvature (φ) and slope (σ) were deduced from a digital terrain model (DTM) on a 50 m resolution grid for the entire study area. They were calculated using the ArcGIS^® 10.2 software Spatial Analyst extension. For all geospatial data sets the same coordinate system (Gauß-Krüger, reference ellipsoid Bessel 1841) was defined.

Table 4: Predictor variables available for this study. The • marks the predictor variables that were used in the final LS Boost-models to reproduce Y_L (BM_YL), Y_R1 (BM_YR1), Y_R2 (BM_YR2) and Y_R3 (BM_YR3).




  
    ID 
    Predictor variable 
    Symbol 
    Y_L
    Y_R1 
    Y_R2 
    Y_R3 
  
  
    1 
    Aspect
    η 
     
     
     
     
  
  
    2 
    Curvature, local
    Φ 
     
     
     
     
  
  
    3 
    Curvature, effective, NE, d₁
    Φ_eff,NE,d1 
    •? 
    •? 
    •? 
    •? 
  
  
    4 
    Curvature, effective, SE, d₁
    Φ_eff,SE,d1 
     
     
    •? 
     
  
  
    5 
    Curvature, effective, SW, d₁
    Φ_eff,SW,d1 
     
     
     
     
  
  
    6 
    Curvature, effective, NW, d₁
    Φ_eff,NW,d1 
     
    ?• 
    ?• 
     
  
  
    7 
    Elevation
    j 
    •? 
    •? 
    •? 
    •? 
  
  
    8 
    Latitude
    • 
     
     
     
     
  
  
    9 
    Longitude
    y 
     
     
     
     
  
  
    10 
    Roughness length, local
    z₀
     
     
     
    •? 
  
  
    11 
    Roughness length, effective, d₁
    z_0eff,d1
     
     
     
     
  
  
    12 
    Roughness length, effective, d₂
    z_0eff,d2
     
     
     
     
  
  
    13 
    Roughness length, effective, d₃
    z_0eff,d3
     
     
     
     
  
  
    14 
    Roughness length, effective, d₄
    z_0eff,d4
     
     
     
     
  
  
    15 
    Roughness length, effective, NE, d₁
    z_0eff,NE,d1
    ?• 
    •? 
    ?• 
    •? 
  
  
    16 
    Roughness length, effective, SE, d₁
    z_0eff,SE,d1
    ?• 
     
    ?• 
     
  
  
    17 
    Roughness length, effective, SW, d₁
    z_0eff,SW,d1
    •? 
    •? 
    •? 
    •? 
  
  
    18 
    Roughness length, effective, NW, d₁
    z_0eff,NW,d1
     
     
    •? 
     
  
  
    19 
    Roughness length, effective, NE, d₂
    z_0eff,NE,d2
     
     
     
     
  
  
    20 
    Roughness length, effective, SE, d₂
    z_0eff,SE,d2
     
     
     
     
  
  
    21 
    Roughness length, effective, SW, d₂
    z_0eff,SW,d2
     
     
     
     
  
  
    22 
    Roughness length, effective, NW, d₂
    z_0eff,NW,d2
     
     
     
     
  
  
    23 
    Slope
    s 
     
     
     
     
  
  
    24 
    Topographic exposure
    ? 
     
    •? 
    ?• 
    •? 
  
  
    25 
    Median wind speed (850 hPa level)
     
     
    •? 
     
    ?•



Table 4:  Predictor variables available for this study. The • marks the predictor
variables that were used in the final LS Boost-models to reproduceY_L (BM_YL), Y_R1
(BM_YR1), Y_R2 (BM_YR2) and Y_R3 (BM_YR3)

Following [71], “effective” z₀- and φ-values were calculated for different directional sectors. This was done to account not only for local surface roughness and terrain characteristics at each grid point itself but also for the surface roughness and terrain characteristics in the upwind fetch. The effective roughness length (z_0,eff) and effective curvature (φ_eff) were calculated for the four direction sectors (NE (0^O-90^O), SE (91^O-180^O), SW (181^O-270^O), NW (271^O-360^O)) and for four different distance ranges (d₁: 50-250 m; d₂: 251-500 m; d₃: 251- 1000 m; d₄: 501-1000 m) for all grid points.

Here, “effective” means that the z0- and f-values available on the 50 m resolution grid were averaged over d1-d4 because surface roughness and terrain characteristics in the immediate vicinity of the DWD-stations strongly affect local wind conditions. The local, isotropic z0-values listed in Table 1 were used for the z0,eff -calculations. The consideration of different directional sectors in the z0,eff - and feff -calculations introduces a minimum of directionality into the proposed model that otherwise has no directional dependence.

Wind speed model building

The proposed statistical wind speed model uses orographic features, surface roughness and reanalysis data to predict WK5- parameters on a 50 m resolution grid in the entire study area. The model is developed by making use of the Ensemble Learning algorithm for least squares boosting (LSBoost) implemented in the Matlab^®Statistics Toolbox. LSBoost uses of a sequence of regression trees called weak learners (B) with the aim to minimize the meansquared error (MSE) between target variable Y and the aggregated prediction of the weak learners (Y_pred) based on methods described in [72]. LSBoost starts with an initial guess of the aggregated prediction of the median of the target variable ( $\tilde{Y}$ ) as a function of the predictor variables (X). Then it combines multiple regression models B₁, …, B_m in a weighted manner to improve its overall predictive performance [73]:

$Y_{p r e d} (X) = \tilde{Y} (X) + ν \sum_{m = 1}^{M} ρ_{m} B_{m} (X)$ (4)

with pm being the weight for model m, M is the total number of weak learners, ν with 0 < ν = 1 being the learning rate.

The LSBoost-models were parameterized using DS1-data and the corresponding values of surface roughness, orographic features and reanalysis data at and in the surroundings of the wind speed measuring stations. The predictive performance of the final LSBoost-models (BM) was evaluated using DS1- and DS2-data. Although finding the optimal number of weak learners is a trial and error process, a low weak learner number (M < 100) should already be sufficient to reasonably approximate Y. Otherwise, a significant improvement of the prediction result will not be achieved by increasing the number of weak learners. LSBoost was chosen to model the WK5-parameters because (i) it is insensitive to outliers, (ii) its stability is maintained during the adjustment process as only simple regression models are added, (iii) irrelevant predictor variables are sorted out and (iv) no data transformation is necessary. Thus, it can be used to reasonably model low quality data [74].

Before the WK5-model building process started, the strength of collinearity among the available predictor variables was tested by evaluating the variance inflation factor (VIF) and the conditions index (CI) in combination with variance-decomposition proportions (VD) according to [75]. By applying these tests, collinearity as quantified by VIF > 2 and/or CI > 30 with VD > 0.5 was not identified among the predictor variables used in the final LSBoost-models.

Since WK5 is a five-parameter distribution, it can be fitted to a large number of shapes. With the choice of appropriate parameters, WK5 can mimic most of the commonly used distributions [65,67]. However, the determination of its parameters might not always be stable. In order to enhance the stability of the WK5-parameter estimation, the WK5-parameters were modeled separately following [70] with a similar but simplified approach. First, the left part of the right-hand side of equation 3 (Y_L) which is represented by α, β and ε was modeled for F = 0.25:

$Y_{L} = ε + \frac{α}{β} [1 - (1 - 0.25) ^{ β}]$ (5)

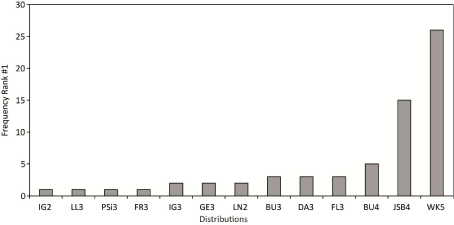
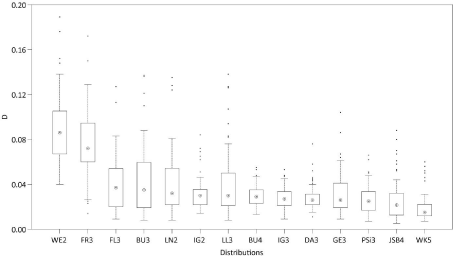
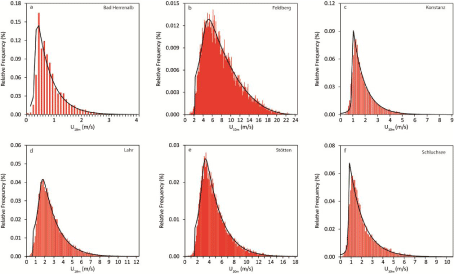
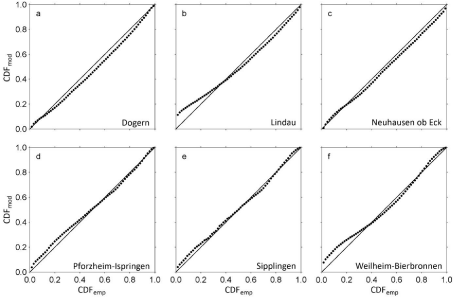
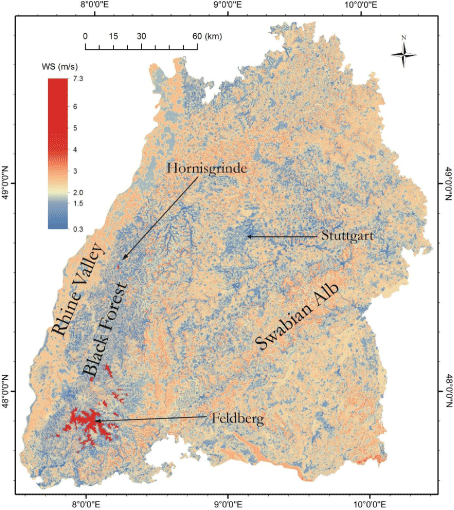
The separation of Y_L from the right part of the right-hand side of equation 3 (Y_R) is justified because Y_L is quasi-constant for F~= 0.25, i.e. distinct changes of Y_L are expected only for empirical values located in the 1st

Next, Y_R, which is represented by γ and δ, was modeled for F= 0.50 (Y_R1), F = 0.75 (YR²) and F = 0.99 (Y_R3). Knowing Y_R1, Y_R2 and Y_R3, the following system of nonlinear equations can be solved to determine γ and δ:

${\begin{cases} \frac{γ}{δ} [1 - (1 - 0.50) ^{- δ}] + [Y_{R 1} - Y_{L}] = 0 \\ \frac{γ}{δ} [1 - (1 - 0.75) ^{- δ}] + [Y_{R 2} - Y_{L}] = 0 \\ \frac{γ}{δ} [1 - (1 - 0.99) ^{- δ}] + [Y_{R 3} - Y_{L}] = 0 \end{cases}$ (6)

After modeling the two parts of the right-hand side of equation 3 separately, Y_L and Y_R were recombined to yield the Wakebydistribution with modeled parameters (WK5_mod). Following [33,76,77], the predictive performance of WK5_mod was evaluated in DS1 and DS2 by the mean error (ME), mean absolute error (MAE), root mean square error (RMSE) and R².

The workflow including data preparation, probability distribution fitting and wind speed model building is summarized in Figure 4.

Figure 4: Schematic representation of the workflow including data preparation, probability distribution fitting and wind speed model building.

    
    
    Figure 4:  Schematic representation of the workflow including data
preparation, probability distribution fitting and wind speed model building.

Results and Discussion

Probability distribution fitting

The absolute frequency of all CDF which ranked at least once best after evaluating the goodness-of-fit by the KS-Test statistic D is shown in Figure 5. It is obvious that WK5 could be fitted most often (at 26 stations) best to CDF_emp. Moreover, based on the evaluation of D, WK5 always ranked between #1 and #10 after being fitted to all 65 CDF_emp. These findings are in accordance with [20] who also report a good performance of WK5 in comparison to other distributions. Only the Johnson SB distribution [78] could also be fitted best to a noteworthy number of CDF_emp (at 15 stations). Since the varieties of the Weibull-distribution (WE2, WE3) never ranked #1, they are not shown.

Figure 5: CDF which ranked at least once best (Rank #1) after being fitted to CDF^emp.

    
    
    Figure 5:  CDF which ranked at least once best (Rank
#1) after being fitted to CDF^emp.

To illustrate the findings of the KS-Test, Figure 6 shows boxplots of D for all distributions that at least once ranked #1 plus the boxplot derived from the D-values determined from fitting WE2 which was used in numerous previous studies as mentioned in the Introduction (results obtained for WE3 are very similar to the results obtained for WE2 and therefore not shown). It is obvious that the D-median of 0.015 obtained from fitting WK5 to CDF^emp is the lowest. In comparison to that, the D-median for WE2 is 0.086. In addition and in comparison to most of the other displayed distributions, the variability of D (e.g. as illustrated by the interquartile range) determined from WK5-fitting is also low.

Figure 6: Boxplots illustrating the variability of the KS-Test statistic D for CDF that ranked at least once best after being fitted to CDF^emp as well as a box plot for D derived from fitting WE2 to CDF^emp.

    
    
    Figure 6:  Boxplots illustrating the variability of the KS-Test statistic D for CDF
that ranked at least once best after being fitted to CDF^emp as well as a box plot
for D derived from fitting WE2 to CDF^emp

The boxplots presented in Figure 7 are based on R²-values which were calculated from P-P plots produced for all distributions that at least once ranked #1 plus WE2. These boxplots are similar to the boxplots presented by [20] and further confirm the WK5-capabilities to reasonably characterize CDF_emp. The median of WK5-related R²- values is 1.000; the interquartile range is represented by R² > 0.999.

Figure 7: Boxplots illustrating the variability of the coefficient of determination (R²) which was calculated from the comparison of CDF of the distributions specified on the x-axis with CDF_emp in P-P plots.

    
    
    Figure 7:  Boxplots illustrating the variability of the coefficient of determination
(R²) which was calculated from the comparison of CDF of the distributions
specified on the x-axis with CDF_emp in P-P plots.

To demonstrate the flexibility of WK5 in fitting U_10m -distributions, Figure 8 shows relative frequency histograms of U_10m from six stations contained in DS1 that were fitted using WK5-probability density functions (WK5_pdf). At station Bad Herrenalb (Figure 8a), the general wind speed level was generally very low and varied in the range 0 m/s to 4 m/s. The corresponding empirical frequency distribution is right-skewed with relative frequency values peaking below 1 m/s. It is obvious that WK5 fits the relative frequency distribution reasonably well. In contrast to that, Figure 8b shows the relative frequency distribution from station Feldberg. At this station which is located on the top of the Feldberg, ${\tilde{U}}_{10m}$ was highest. The wind speed range on the x-axis includes U_10m -values up to 24 m/s. The relative frequency distribution is also skewed to the right and peaks in the U_10m -range of 5 m/s to 6 m/s. The relative frequency distributions shown in Figure 8c (station Konstanz) to Figure 8f (station Schluchsee) exemplarily represent U_10m -ranges between the rather low U_10m -values recorded at station Bad Herrenalb and the high U_10m-values from station Feldberg. The relative frequency distributions are also right-skewed without exception and more peaked than the normal distribution.

Figure 8: Relative frequency histograms of U_10m presented for the six stations (a) Bad Herrenalb, (b) Feldberg, (c) Konstanz, (d) Lahr, (e) Stötten and (f) Schluchsee which are included in DS1.The black lines represent corresponding WK5_pdf.

    
    
    Figure 8:  Relative frequency histograms of U_10m presented for the six
stations (a) Bad Herrenalb, (b) Feldberg, (c) Konstanz, (d) Lahr, (e) Stötten
and (f) Schluchsee which are included in DS1.The black lines represent
corresponding WK5_pdf.

The Wakeby-distribution has the ability to fit almost all quantiles of the presented relative frequency distributions with sufficient accuracy. Especially, wind speed values located in the 2nd to 4th quartile are fitted well which is crucial for wind energy applications [2,20]. However, the limited potential of WK5 to fit the lowest levels of wind speed is obvious. This behavior of WK5 can be attributed to the facts that (i) its domain of definition is bounded by e at the lower tail and (ii) the lowest wind speed values are most affected by the immediate surroundings of the measurements sites, which cannot be properly reproduced by WK5.

Wind speed model development

The selection of the final predictor variable combinations was a trial and error process. It started with keeping M = 20. The final BMconfiguration was chosen after comparing the predictive performance of several configurations with different combinations of predictor variables. The predictor variable combination which simultaneously gave the lowest MAE-values in DS1 and DS2 was selected as predictor variable combination to build BM. After the final predictor variable combinations were certain, M was increased to further minimize MAE. The final number of weak learners varied between M = 30 for modeling F = 0.75 and M = 97 for modeling F = 0.99.

The predictor variables having the strongest univariate linear association (|R| > 0.5) with any of Y_L, Y_R1, Y_R2 and Y_R3 were τ, φ_eff,NE,d1 and φ_eff,SE,d1. The predictor variable combinations which reproduced Y_L, Y_R1, Y_R2 and Y_R3best are summarized in Table 4. They were fed into the final LSBoost-models BM_YL, BM_YR1, BM_YR2 and BM_YR3 to reproduce the WK5-parameters associated with the wind speed time series contained in DS1 and DS2.

The combinations of predictor variables that were used in this study to model near-surface wind speed distributions are similar to combinations of predictor variables used in previous studies. The regression equation-based statistical wind field model reported by [79] estimates mean annual wind speed as a function of elevation, latitude, longitude, surface shape and surface roughness in Germany on a 200 m resolution grid. Without accounting for surface roughness, [80] used generalized additive models to estimate maximum daily gust speed (98 percentile) in Switzerland on a 50 m resolution grid based on landform, elevation, curvature and slope.

To examine the modeling accuracy of WK5_mod, it was used to estimate CDF_emp. The quality of WK5_mod-estimated CDF_emp (CDF_mod) was evaluated by ME, MAE, RMSE and R². The results of this evaluation are given in Table 5 for various quantiles. As can be expected, the prediction results are in most cases better for DS1 than for DS2. They demonstrate that there is a tendency that with increasing quantiles the absolute prediction error increases, both in DS1 and DS2. This is mainly attributable to increasing wind speed represented by increasing quantiles. However, the prediction errors are generally small and, except for F = 0.99, in the typical range of wind speed measuring accuracy. Except for F = 0.01 associated with DS1, R² is at least 0.80, which further indicates that WK5_mod reasonably reproduces the analyzed quantiles. To illustrate the modeling abilities of WK5_mod for individual stations, Figure 9 shows CDF_mod plotted against CDFemp of six stations contained in DS2 which were not part of the model parameterization process. The closer the data to the 1:1 line, the better the agreement between CDF_mod and CDFemp. It is clear, that if distinct deviations of the presented data from the 1:1 line occur, then they occur in the low quantile range (e.g. Figures 9b,9f). The low quantiles correspond to low wind speed values which are most probably a direct result of small-scale surface and terrain characteristics that are not always correctly reproduced by WK5_mod. Furthermore, its domain of definition causes WK5 to be prone to overestimate the frequency of lower wind speeds [20].

Data set	Quantiles	ME (m/s)	MAE (m/s)	RMSE (m/s)	R²
DS1	0.01	-0.03	0.15	0.26	0.75
	0.25	-0.02	0.14	0.21	0.96
	0.50	0.00	0.14	0.19	0.98
	0.75	0.01	0.18	0.24	0.98
	0.99	0.04	0.31	0.40	0.98
DS2	0.01	-0.03	0.17	0.22	0.59
	0.25	0.03	0.10	0.13	0.92
	0.50	0.09	0.16	0.20	0.93
	0.75	0.11	0.27	0.34	0.90
	0.99	0.15	0.78	0.96	0.80

Statistical Modeling of Near-surface Wind Speed: A Case Study from Baden-Wuerttemberg (Southwest Germany)

Abstract

Introduction

Material and Methods

Study area

Wind speed data

Data preparation

Probability distribution fitting

Geographic data

Wind speed model building

Results and Discussion

Probability distribution fitting

Wind speed model development

Abstract

Acknowledgement

References