Various Gradients of the Second Phase of the Viral Kinetics of Hepatitis C Virus Infection Drawn using the Rapid Equilibrium Model

Research Article

J Hepat Res. 2014;1(3): 1011.

Various Gradients of the Second Phase of the Viral Kinetics of Hepatitis C Virus Infection Drawn using the Rapid Equilibrium Model

Toshiaki Takayanagi*

Sapporo Ryokuai Hospital, Japan

*Corresponding author: Toshiaki Takayanagi, Sapporo Ryokuai Hospital, 1-1, Kitano, Kiyota-Ku, Sapporo, Hokkaido, 004-0861, Japan

Received: August 19, 2014; Accepted: August 30, 2014; Published: August 30, 2014

Abstract

Mathematical models of Hepatitis C Virus (HCV) infection during antiviral treatment have revealed the major mechanism of the function of Interferon (IFN) and the estimated clearance rates of HCV virions and HCV-infected cells. However, differences in the estimated clearance rates of infected cells have been observed between subjects who are and are not treated with Protease Inhibitor. In this study, the author demonstrated that various gradients in the second phase were difficult to obtain by regulating the efficacy of treatment in the predominately used basic model but were easily obtained by regulating the clearance rate of infected cells. The author considers that the estimated clearance rate of infected cells differs depending on the type of treatment because fitting the second phase in the basic model to viral load by regulating efficacy is difficult; however, fitting the second phase by regulating the clearance rate of infected cells is not difficult. Consequently, different infected-cell clearance rates were obtained for different types of treatments. Previously, the author proposed the Rapid Equilibrium (RE) model, which is capable of displaying viral kinetics without rebounds or oscillations under some conditions. In this study the author demonstrated the applicability of the RE model by displaying various gradients of the second phase with various efficacies of treatment.

Keywords: HCV; Mathematical Model; Viral Hepatitis; Rapid Equilibrium Model

Abbreviations

HCV: Hepatitis C Virus; HCC: Hepatocellular Carcinoma; IFN: Interferon; RBV: Ribavirin; PEG-IFN: Pegylated Interferon; PI: Protease Inhibitor; SVR: Sustained Virological Response; HIV: Human Immunodeficiency Virus; HBV: Hepatitis B Virus; RE: Rapid Equilibrium

Introduction

Hepatitis C Virus (HCV) is known to cause chronic hepatitis, liver cirrhosis and Hepatocellular Carcinoma (HCC) and infects approximately 130 to 150 million people worldwide [1]. Interferon (IFN) mono-therapy, IFN in combination with Ribavirin (RBV), Pegylated Interferon (PEG-IFN) mono-therapy and PEG-IFN in combination with RBV have been prescribed to chronic HCV hepatitis subjects. Recently, Protease Inhibitor (PI) has been administered to HCV genotype 1-infected subjects [2-4]. Despite drug-resistant mutations and serious side effects on the skin, the administration of PI improves the rate of Sustained Virological Response (SVR), which is defined as the absence of detectable serum HCV RNA 24 weeks after the cessation of treatment. Similar to Human Immunodeficiency Virus (HIV) infection [9,10] and Hepatitis B Virus (HBV) hepatitis [8,11-13], HCV hepatitis has been analyzed using various mathematical models [5-8]. Moreover, the clearance rates of HCV virions and HCV-infected cells have been estimated in mathematical studies [4,5,14-16]; however, the estimated HCVinfected cell clearance rates of subjects treated with and without PI are different [4]. The infected-cell clearance rate of subjects treated with PI is estimated to be approximately ten times higher than that of subjects treated without PI [4] Adiwijaya et al, assumed different infected-cell clearance rates for subjects treated with and without PI [17], and Adiwijaya et al. assumed that clearance rates depended on the efficacy of treatment [18]. However, PI, which inhibits the protease of HCV, is not expected to directly increase the infected-cell clearance rate.

The author published a study dealing the Rapid Equilibrium (RE) model for chronic viral hepatitis during anti-viral treatment [8]. In the previous study, the author demonstrated that the RE model could exhibit viral kinetics without rebounds or oscillations under some conditions. In the present paper, the author compared the wellknown basic model [5] with the RE model [8], particularly in terms of the second viral decline. The author discusses the discrepancy in the estimated infected-cell clearance rates between subjects who are treated with and without PI.

Materials and Methods

Modeling

Basic model

The basic model [5] of viral infection is described by equation (1) below:

{ dT dt =s− δ T T−(1−η) β 1 VT dI dt =(1−η) β 1 VT− δ I I dV dt =(1−ε)pI−cV                                       (1) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaeaafaqabeWabaaabaWaaSaaaeaaieaacaWFKbGaamivaaqaaiaa=rgacaWG0baaaiabg2da9iaadohacqGHsislcqaH0oazdaWgaaWcbaGaamivaaqabaGccaWGubGaeyOeI0IaaiikaiaaigdacqGHsislcqaH3oaAcaGGPaGaeqOSdi2aaSbaaSqaaiaaigdaaeqaaOGaamOvaiaadsfaaeaadaWcaaqaaiaa=rgacaWGjbaabaGaa8hzaiaadshaaaGaeyypa0JaaiikaiaaigdacqGHsislcqaH3oaAcaGGPaGaeqOSdi2aaSbaaSqaaiaaigdaaeqaaOGaamOvaiaadsfacqGHsislcqaH0oazdaWgaaWcbaGaamysaaqabaGccaWGjbaabaWaaSaaaeaacaWFKbGaamOvaaqaaiaa=rgacaWG0baaaiabg2da9iaacIcacaaIXaGaeyOeI0IaeqyTduMaaiykaiaadchacaWGjbGaeyOeI0Iaam4yaiaadAfaaaaacaGL7baacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabIcacaqGXaGaaeykaaaa@8534@

Where T is the number of target cells, I is the number of infected cells, and V is the viral load. Target cells are produced at rate s and die at rate δT. Target cells become infected at rate β1V, and infected cells die at rate δI. HCV virions are produced by an infected cell at rate p and are cleared at rate c. Antiviral treatment reduces the infection rate by the fraction (1 - η) and/or the viral production rate by the fraction (1 - ε).

Rapid equilibrium model

The RE model [8] is described by equation (2) below:

{ dT dt =s− δ T T− (1−η) β 2 VT K+V dI dt = (1−η) β 2 VT K+V − δ I I dV dt =(1−ε)pI−cV                              (5) MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaeaafaqabeWabaaabaWaaSaaaeaaieaacaWFKbGaamivaaqaaiaa=rgacaWG0baaaiabg2da9iaadohacqGHsislcqaH0oazdaWgaaWcbaGaamivaaqabaGccaWGubGaeyOeI0YaaSaaaeaacaGGOaGaaGymaiabgkHiTiabeE7aOjaacMcacqaHYoGydaWgaaWcbaGaaGOmaaqabaGccaWGwbGaamivaaqaaiaadUeacqGHRaWkcaWGwbaaaaqaamaalaaabaGaa8hzaiaadMeaaeaacaWFKbGaamiDaaaacqGH9aqpdaWcaaqaaiaacIcacaaIXaGaeyOeI0Iaeq4TdGMaaiykaiabek7aInaaBaaaleaacaaIYaaabeaakiaadAfacaWGubaabaGaam4saiabgUcaRiaadAfaaaGaeyOeI0IaeqiTdq2aaSbaaSqaaiaadMeaaeqaaOGaamysaaqaamaalaaabaGaa8hzaiaadAfaaeaacaWFKbGaamiDaaaacqGH9aqpcaGGOaGaaGymaiabgkHiTiabew7aLjaacMcacaWGWbGaamysaiabgkHiTiaadogacaWGwbaaaaGaay5EaaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGOaGaaeynaiaabMcaaaa@84B9@

Where the parameter K is analogous to the Michaelis constant Km, i.e., K is the viral load for the half-maximal production of infected hepatocytes from uninfected hepatocytes and virus. Target cells become infected at rate β2V/(K+V).

Values of the Parameters

To investigate the differences between the basic model and the RE model, the following identical values based on previous studies [5,16] were used: initial V(V0) = 1x106 virions ml-1; δT = 0.003 day-1; δI = 0.51day-1; p= 100 virions cell-1 day-1; and c = 12.2 day-1.

In the previous study [8], the author assumed β1 = 2.25x10-9 virions-1 ml day-1 to exhibit various biphasic viral declines with various values of parameter ε. In this study, β1= 3x10-7 virions-1 ml day-1 was assumed, because the value of parameter β1 was assumed to be numbers in minus seven figures in the previous studies [5-7].

Results

Figure 1 A and B show the simulations of the basic model and the RE model, respectively, from day 0 to 28 with various values of parameter ε. In Figure 1A, as the value of ε increases between 0.8 and 0.999, the first viral decline increases. In contrast, the gradient of the second phase changes only minimally while 0.95≤ε ≤ 0.999. However, when ε = 0.9, a downwardly convex curve was obtained in the second phase of viral decline, and when ε = 0.8, a rebounding curve was obtained in the second phase.

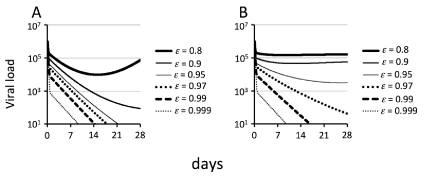
Figure 1: Simulations of the basic model and the RE model during antiviral therapy with different drug efficacies Simulations of the basic model (A) defined by equation (1) and the RE model (B) defined by equation (2) were performed from day 0 to 28. In all simulations, the following parameters were held constant: δT = 0.003 day-1; δI = 0.51day-1; p =100 virions cell-1 day-1; c = 12.2 day-1; t0 =2.4 hours; and η = 0. The drug efficacy values (ε) are indicated in each panel. (A) Viral load calculated with s = 6.28422x104 cells ml-1day-1 and β1 = 3.0x10-7 virions-1 ml day-1. (B) Viral load calculated with s = 7.11382x104 cells ml-1day-1, β2=2.25x10-2 day-1 and K =7.5x104 virions ml-1.

    

    
    

    

    Figure 1:  Simulations of the basic model and the RE model during antiviral therapy with different drug efficacies
Simulations of the basic model (A) defined by equation (1) and the RE model (B) defined by equation (2) were performed from day 0 to 28. In all simulations, the following parameters were held constant: δT = 0.003 day-1; δI = 0.51day-1; p =100 virions cell-1 day-1; c = 12.2 day-1; t0 =2.4 hours; and η = 0. The drug efficacy values (ε) are indicated in each panel. (A) Viral load calculated with s = 6.28422x104 cells ml-1day-1 and β1 = 3.0x10-7 virions-1 ml day-1. (B) Viral load calculated with s = 7.11382x104 cells ml-1day-1, β2=2.25x10-2 day-1 and K =7.5x104 virions ml-1.

As shown in Figure 1B, as the value of ε increases between 0.8 and 0.999, the first viral decline increases as in Figure 1A. Furthermore, the gradient of the second phase decreases as the value of ε decreases between 0.97 and 0.999. When ε = 0.95, a downwardly convex curve was obtained in the second phase of viral decline, and when ε = 0.8 and 0.9, flat phases were obtained after the first phase of viral decline.

To confirm the ease of obtaining various gradients of the second phase using the basic model with various values of δp, Figure 2 shows the simulations using the basic model from day 0 to 28 with various values of parameter δI. To maintainV0 = 1x106 virions ml-1, the values of parameters were obtained by equation (4). Figure 2 shows the viral kinetics with δI = 0.05, 0.1, 0.2, 0.3, 0.4 and 0.51 day-1, and s = 6.161x103, 1.2322x104, 2.4644x104, 3.6966x104, 4.9288x104 and 6.28422x104 cell ml-1 day-1, respectively. A comparison of Figure 1A and Figure 2 reveals that, as expected, the regulation of δI was more effective in changing the gradient of the second phase than the regulation of ε.

Figure 2:

Simulations of the basic model during antiviral therapy with various values of parameters s and δI

Simulations of the basic model defined by equation (1) were performed from day 0 to 28. In all simulations, the following parameters were held constant: δT = 0.003 day-1; β1 = 3.0x10-7 virions-1 ml day-1; p = 100 virions cell-1 day-1; c = 12.2 day-1; t0 = 2.4 hours; η = 0; and e = 0.99. To maintain V0 = 1x106 virions ml-1, the value of parameter s was calculated for each value of δI by equation (4). For the sake of clarity of the figure, only the values of δI are indicated in the graph, and s = 6.161x103, 1.2322x104, 2.4644x104, 3.6966x104, 4.9288x104 and 6.28422x104 cell ml-1 day-1 when δI = 0.05, 0.1, 0.2, 0.3, 0.4 and 0.51 day-1, respectively.

    

    
    

    

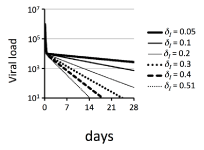
    Figure 2:  
Simulations of the basic model during antiviral therapy with various values of parameters s and δI

Simulations of the basic model defined by equation (1) were performed from day 0 to 28. In all simulations, the following parameters were held constant: δT = 0.003 day-1; β1 = 3.0x10-7 virions-1 ml day-1; p = 100 virions cell-1 day-1; c = 12.2 day-1; t0 = 2.4 hours; η = 0; and e = 0.99. To maintain V0 = 1x106 virions ml-1, the value of parameter s was calculated for each value of δI by equation (4). For the sake of clarity of the figure, only the values of δI are indicated in the graph, and s = 6.161x103, 1.2322x104, 2.4644x104, 3.6966x104, 4.9288x104 and 6.28422x104 cell ml-1 day-1 when δI = 0.05, 0.1, 0.2, 0.3, 0.4 and 0.51 day-1, respectively.

Discussion

In the present study, the author demonstrated that the gradient of the second phase of viral decline changed according to changes inefficacy using the RE model shown in Figure 1B. As the clinical data [3,19] show, the first and second phases depend on efficacy as in Figure 1B. However, the author was unable to obtain the viral kinetics similar to those reported in the clinical data using the basic model with β1 = 3x10-7 virions-1 ml day-1 as shown in Figure 1A. The second phase changed only minimally while 0.95≤ε≤0.999; furthermore, the second phase became a rebounding curve when ε =0.8.

Because the administration of PI improves the rate of SVR, the value of parameter ε should be larger with PI treatment than without PI treatment. Although PI is not expected to directly increase the infected-cell clearance rate, the infected-cell clearance rate was assumed to be larger in the subjects who are treated with PI than in those who are not treated with PI [4,17,18]. The author doubted the veracity of the discrepancy in the estimated infected-cell clearance rates, which led the author consider the following thought process. When fitting the basic model to HCV RNA viral load, one has to estimate the value of parameter ε as large for the second phase to be straight. Then, one must fit the second phase to the HCV RNA viral load by regulating the value of the infected-cell clearance rate. Consequently, the infected-cell clearance rate of the subjects who are treated with PI is estimated to be larger than of the subjects who are treated without PI. Thus, the administration of treatments that are more effective than the current available therapies would necessitate estimate even larger estimations of the infected-cell clearance rate.

In the previous study [8], the author suggested that the basic model is capable of explaining early viral kinetics during therapies but is incapable of explaining long-term viral kinetics. Under the conditions utilized in this paper, the basic model might not be able to explain the second phase. The author considers that the RE model might be more appropriate for analyzing the second phase than the basic model because the RE model is capable of exhibiting the various gradients of the second phase according to various values of parameter ε as shown in Figure 1B.

The discrepancy in the estimated infected-cell clearance rates was investigated in this study. The author considers that we have to assure whether the values of the other parameters are also reasonable medically. Because a new problem of drug resistant mutations has occurred, modeling HCV infection during treatment has to be more complicated [17,18]. Nevertheless, in the future, modeling HCV infection will help us with making predictions of treatment outcomes clinically.

Conclusion

In the present study, the author compared the basic model [5] to the RE model [8] in terms of the second phase. Under the conditions of this study, regulating the efficacy of treatment in the basic model was incapable of producing a trend in the second phase that mimicked the clinical data [3,19]; however, regulating the infected-cell clearance rate was capable of mimicking this phase. The author considers that the estimated infected-cell clearance rate differs depending on the type of treatment because fitting the second phase in the basic model to viral load by regulating efficacy is difficult, but fitting it by regulating the infected-cell clearance rate is not difficult. In contrast, regulating the efficacy of treatment in the RE model was able to produce a trend in the second phase that mimicked the clinical data [3,19].The author considers that the RE model is thus more appropriate for analyzing the second phase.

References

  1. Reilly P. The impact of neurotrauma on society: an international perspective. Prog Brain Res. 2007; 161: 3-9.
  2. Reesink HW, Zeuzem S, Weegink CJ, Forestier N, van Vliet A, van de Wetering de Rooij J, et al. Rapid decline of viral RNA in hepatitis C patients treated with VX-950: a phase Ib, placebo-controlled, randomized study. Gastroenterology. 2006; 131: 997-1002.
  3. Forestier N, Reesink HW, Weegink CJ, McNair L, Kieffer TL, Chu HM, et al. Antiviral activity of telaprevir (VX-950) and peginterferon alfa-2a in patients with hepatitis C. Hepatology. 2007; 46: 640-648.
  4. Adiwijaya BS, Hare B, Caron PR, Randle JC, Neumann AU, Reesink HW, et al. Rapid decrease of wild-type hepatitis C virus on telaprevir treatment. Antivir Ther. 2009; 14: 591-595.
  5. Neumann AU, Lam NP, Dahari H, Gretch DR, Wiley TE, Layden TJ, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science. 1998; 282: 103-107.
  6. Dahari H, Shudo E, Cotler SJ, Layden TJ, Perelson AS. Modelling hepatitis C virus kinetics: the relationship between the infected cell loss rate and the final slope of viral decay. Antivir Ther. 2009; 14: 459-464.
  7. Dahari H, Lo A, Ribeiro RM, Perelson AS. Modeling hepatitis C virus dynamics: liver regeneration and critical drug efficacy. J Theor Biol. 2007; 247: 371-381.
  8. Takayanagi, T. Modeling chronic hepatitis B or C virus infection during antiviral therapy using an analogy to enzyme kinetics: Long-term viral dynamics without rebound and oscillation. Computers in biology and medicine 2013; 43: 2021-2027.
  9. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996; 271: 1582-1586.
  10. Takayanagi T, Ohuchi A. Computer simulations of slow progression of human immunodeficiency virus infection and relapse during anti-HIV treatment with reverse transcriptase inhibitors and protease inhibitors. Microbiol Immunol. 2002; 46: 397-407.
  11. Nowak MA, Bonhoeffer S, Hill AM, Boehme R, Thomas HC, McDade H. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci USA. 1996; 93: 4398-4402.
  12. Tsiang M, Rooney JF, Toole JJ, Gibbs CS. Biphasic clearance kinetics of hepatitis B virus from patients during adefovir dipivoxil therapy. Hepatology. 1999; 29: 1863-1869.
  13. Lewin SR, Ribeiro RM, Walters T, Lau GK, Bowden S, Locarnini S, et al. Analysis of hepatitis B viral load decline under potent therapy: complex decay profiles observed. Hepatology. 2001; 34: 1012-1020.
  14. Herrmann E, Lee JH, Marinos G, Modi M, Zeuzem S. Effect of ribavirin on hepatitis C viral kinetics in patients treated with pegylated interferon. Hepatology. 2003; 37: 1351-1358.
  15. Herrmann E, Zeuzem S, Sarrazin C, Hinrichsen H, Benhamou Y, Manns MP, et al. Viral kinetics in patients with chronic hepatitis C treated with the serine protease inhibitor BILN 2061. Antivir Ther. 2006; 11: 371-376.
  16. Guedj J, Perelson AS. Second-phase hepatitis C virus RNA decline during telaprevir-based therapy increases with drug effectiveness: implications for treatment duration. Hepatology. 2011; 53: 1801-1808.
  17. Adiwijaya BS, Herrmann E, Hare B, Kieffer T, Lin C, Kwong AD, et al. A multi-variant, viral dynamic model of genotype 1 HCV to assess the in vivo evolution of protease-inhibitor resistant variants. PLoS Comput Biol. 2010; 6: 1000745.
  18. Adiwijaya BS, Kieffer TL, Henshaw J, Eisenhauer K, Kimko H, Alam JJ, et al. A viral dynamic model for treatment regimens with direct-acting antivirals for chronic hepatitis C infection. PLoS Comput Biol. 2012; 8: 1002339.
  19. Kieffer TL, Sarrazin C, Miller JS, Welker MW, Forestier N, Reesink HW, et al. Telaprevir and pegylated interferon-alpha-2a inhibit wild-type and resistant genotype 1 hepatitis C virus replication in patients. Hepatology. 2007; 46: 631-639.

Citation: Takayanagi T. Various Gradients of the Second Phase of the Viral Kinetics of Hepatitis C Virus Infection Drawn using the Rapid Equilibrium Model. J Hepat Res. 2014;1(3): 1011. ISSN:2381-9057