Baltas EA; Panagos DS

Research Article

Austin J Hydrol. 2014;1(2): 5.

Sensitivity Analysis of the Error Contribution of Terminal Velocity of Drops, Using Joss-Waldvogel Disdrometer Data

Baltas EA* and Panagos DS

Department of Water Resources Hydraulic and Maritime Engineering, National Technical University of Athens, Greece

*Corresponding author: Baltas EA, Department of Water Resources Hydraulic and Maritime Engineering, National Technical University of Athens, 15780, 5, Iroon Polytechniou, 15780 Athens, Greece

Received: June 24, 2014; Accepted: September 15, 2014; Published: September 25, 2014

Abstract

In the present work, a sensitivity analysis is taking place, in order to investigate the extent of error produced by the embedded terminal velocity theoretical relationship in the algorithm of a Joss Waldvogel RD-69 disdrometer. For that reason a cross analysis is conducted between the measurements of two conventional rain gauges against a Joss-Waldvogel RD-69 disdrometer collocated in the meteorological station of the campus of National Technical University of Athens. All instruments are placed in a distance no longer than a few meters apart therefore justifying the correlation of their measurements. The data used were collected during a 9 year period. Terminal velocity is defined as the velocity of a rain drop when the drag force applied by the air friction is equal to the gravity force, in a state of equilibrium. Actually it is a raindrop characteristic very difficult to model, that varies according to the shape and the equivalent diameter of each drop (if it is considered a sphere with the same mass) but also to other factors like air density, atmospheric pressure, temperature, drop breakup and coalescence, the wind direction and speed and local updraft or downdraft wind phenomena. Classical theoretical formulae take into account only the variation of the equivalent diameter (and respectively the mass) of the rain drop in order to estimate the terminal velocity. Rain drops falling with terminal velocity different than the one anticipated by theoretical formulas are a source of error in the estimation of the rain intensity and the rest hydro-meteorological characteristics of rain, in measurement instruments like disdrometers.

A selection of rainfall events has been conducted, that was based on the next criteria: Only extreme events of duration more than 20 min have been selected, that the actual rain amount exceeded 10 mm in the referred time duration, resulting in mean rainfall rates over the value of 30.0 mm/h (heavy rain) in order to get more representative raindrop size distributions (DSDs), with counts on a diversity of bins. Heavy rains have been selected for an additional reason: the turbulence phenomena of wind and the other factors that affect the terminal velocity of the recorded rain drops by the Joss-Waldvogel disdrometer, are of increased importance, therefore differences in the measurements among the various instruments can be identified with more ease.

Theory

Small cloud droplets (d<0.05mm) are almost spherical and the flow around them can be considered laminar. For these droplets the terminal velocity of fall can be found by equating the force of gravity (Fg=gρ_wpd³/6) to friction (Fd=3pdmV) yielding Stokes law [1].

V_{t} = \frac{ρ_{w} g d^{2}}{18 μ} (1)

Where Vt is the terminal velocity of fall, ρ_w, is the density of water, g the acceleration of gravity, d the diameter of the drop and μ the dynamic viscosity of air (μ=18*10^-6 Pa at 20°C.).

Larger drops fall faster and the flow around them becomes turbulent. The shape of the drops also is different than the theoretical spherical one and becomes more elliptical to the horizontal axis. Rain drops are usually sized between 1-5 mm but there are cases that a drop can exceed 7 mm. As the velocity of the air increases so does the air frictional force, drag. There are two classes of drag force balance against the downward force of gravity:

Diffusive or viscous

The surface drag force acts along the sides of the droplet, fighting against the velocity shear. Two forms of viscous force are identified: Stokes drag where molecular viscosity dominates and eddy drag where drag is associated with eddies.

Dynamic pressure. The drag force is due to the collision of the air molecules with the droplet, across the falling surface area.

In a state of equilibrium the gravitational force is equal to drag and eventually a rain drop is falling with a constant speed, the terminal velocity.

In this case terminal velocity is given by the next relationship:

V_{t} = \sqrt{\frac{2 m g}{ρ_{a} A C_{d}}} (2)

Where

ρ_α is the density of air (about 1.2 kg/m³).

A is a cross-sectional area of the object. If the object was a sphere, this area would be the area of a circle.

m is the mass of the falling object, g is the acceleration of gravity and C_d is the drag coefficient. This depends on the shape of the object. A cone and a flat circle will have the same A, but different drag coefficients. C_d is depended on the Reynolds number, according to the relationship [2]:

C_{D} = C_{o} {(1 + \frac{δ_{0}}{\sqrt{Re}})}^{2} (3),

Where C_o, δ_o coefficients equal to 0.29 and 9.06 respectively

and

Re = \frac{D V}{v} (4)

where D is the diameter, V the velocity and v the kinematic viscosity of the fluid medium.

Re can be estimated by an indirect procedure: One can assume a velocity V, find a Re number, replace in equation (3), find a CD and then return to equation. (2) to verify the assumed terminal velocity. Usually the process is finished with a small number of iterations if the initial value for V_t is properly chosen.

The terminal velocity depends on the air density and this relation can be approximated by the following [3]:

V_{t} = V_{o} {(\frac{ρ_{a}}{ρ_{o}})}^{b - 1} (5)

Where ρ_α, is the density of air in the site of the measured velocity, ρ_o is the air density at sea level, b is a coefficient (usually 0.4-0.6) and V_o is the terminal velocity expressed by Gunn and Kinzer [4] measurements.

In general several empirical relations have been proposed for the estimation of the terminal velocity of rain drops, like the power law in the form of:

V_{t} = a D^{β} (6)

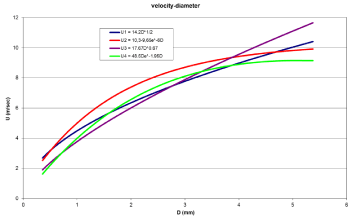
where D is the diameter of the equivalent sphere of the same mass with the actual drop and α, β coefficients, proposed by Atlas and Ulbich [5] among others with the values for the coefficients a=17.67 and b=0.67, or a=14.2 and b=0.5 the relationship proposed by Best [6]:

V_{t} = 10.30 - 9.65 \exp (- 0.6 D) (7)

The relationship proposed by Gossard [7]:

V_{t} = 9.65 (1 - \exp (- 0.53 D) (8)

The relationship proposed by Uplinger [8]:

V_{t} = 48, 5 D \exp (- 1, 95 D) (9)

equation (6), D is in mm while in equations (7), (8) and (9) D is in cm and Vt is in m/sec.

In relative works also theoretical formulas have been derived regarding the expression of terminal velocity [9].

Rain drop coalescence and break up are two distinct mechanisms that affect the terminal velocity of rain drops. When two drops collide just before hitting the surface of a measurement instrument, the result is a bigger drop that actually travels with a terminal velocity equal to the velocity of the previous smaller diameters common velocity, and not the bigger velocity of the respective merged diameter. On the contrary when a bigger drop breaks up in two smaller ones, the common velocity of the spitted drops is bigger than the theoretical one, because is the terminal velocity of the initial bigger drop [3]. From the above it is derived that uncertainty is introduced since there is not one-to-one correspondence between terminal fall speed and apparent drop size [10].

The terminal velocity is used for the derivation of the rain intensity (and the respective rain amount) with the help of the Joss-Waldvogel disdrometer according to the next relationship: [11].

R = \frac{π}{6} \int_{0}^{\infty} N_{(D)} D^{3} U_{(D)} d D (10)

On the above relationship the rain amount is proportional to the terminal velocity of each class of drops. The Joss-Waldvogel RD-69 disdrometer divides the measured drops in twenty classes or bins so equation (10) is equivalent with the sum of the products of the respective 20 classes of diameters. Moreover the terminal velocity is essential component in the derivation of a group of equally important hydro-meteorological parameters such as the radar reflectivity factor Z, the water liquid content W, the Energy Flux EF, etc., with the use of a Joss-Waldvogel disdrometer.

Joss-Waldvogel RD-69 Limitations

The major limitations of the Joss-Waldvogel RD 69 disdrometer [12] are:

The instrument can't measure directly the terminal velocity or the diameter of every drop. Instead the cumulative impact of the speed and the mass (kinetic energy of the drop) is been transformed in drum displacement producing an electrical signal and finally turning into a drop count.
There is a structural inability to measure diameter drops of more than 5.101 mm. Therefore every drop having a bigger diameter is measured in the last bin class, underestimating its size.
Also there is a structural inability to measure diameter drops of less than 0.313 mm. Therefore every drop with smaller diameter is cut of as "noise" by the analyzer of the instrument.
The instrument is affected by external noise and air fluctuations interfering with the sensitive impact drum, so errors may occur in extreme rain events.
Finally the instrument can produce measurement errors according to the "dead time error" effect. When a large drop hits the instrument a following drop can only be measured after a small time interval that depends on the size of the drop, due to the time duration the electro-mechanical inner system needs to return to the initial measuring position (before the hit). Dead time error is responsible for the absence of counts in the smaller bins when heavy rain events occur.

The following empirical function was developed for calculating a correction for this dead time [13]:

N_{i} c o r r = N_{i} \exp [\frac{0.035}{T} \sum_{D k = 0.85 D i}^{D k \max} \ln \frac{D_{k}}{0.85 (D_{i} - 0.25)}] (11)

Where N_i is the number of drops in size class i without correction,

N_i corr is the number of drops in size class i with correction,

T in the sampling time in seconds,

A drop in size class k causes a dead time for all channels i where, D_k=0.85 D_i

Methodology

The following instruments have been used:

A Joss-Waldvogel RD 69 disdrometer.
An Arg-100 rain gauge by Campbell Scientific Inc.
A Rain-O-Matic rain gauge by Pronamic.

In order to investigate measurement differences in a more clear and reliable way we have set the following criteria of analysis:

The selected rainfall events total duration exceeded 20 min.
The selected rainfall events total amount of precipitation exceeded 10 mm in the minimum duration of 20 min (resulting in more than 30 mm/h mean rain intensity)

Special attention was given to these intense events because they impose great flooding danger for the greater Athens region. This is due to considerable spatiotemporal gradients which make the correct estimation of the amount of precipitation during such events both very important and challenging [14]. The data series of the conventional rain gauges are available in the address "www.hoa.ntua.gr" and due to their substantial size (above common spreadsheets capabilities) are going to be processed with the "Hydrognomon" application, developed under the research team of NTUA and available for free download.

The values of instruments b and c where used as default, while their values (with 10 min time step) were averaged in order to get more reliable results. In this point we have to refer that also instruments b and c have inherent sources of measurement errors, like:

The effect of strong winds distracting the rain drops from entering the measurement cones,
The measurement "dead time error" between the tilting of the internal mechanisms of the instruments, when they are full of rain water and move downwards until they are restored in the initial position which enables them to measure the next tip.

Regarding the effect of the wind turbulence, due to the proximity of all instruments to each other, we can assume that it affects the instruments in the same extent, so strong winds cannot be considered a source of error that is affecting a particular instrument in a quantitatively favored way. Nevertheless strong winds, like updrafts and downdrafts effect the terminal velocity of rain drops measured by the Joss-Waldvogel disdrometer and play an important role in our cross analysis.

As for measurement error No "II" an additional criterion has been imposed:

If the raw values of each of the instruments b or c deviated more than 15%, from the average value, then the rain event was discarded.

As referred previously, the terminal velocity according to equation (5) is depended on the altitude of the measurement. For that reason an additional correction has been estimated due to the fact that the meteorological station is sited in altitude of 181 m above sea level. This correction resulted in terminal velocities multiplied by the factor (assuming b=0.6):

V_{t} = V_{o} {(\frac{ρ_{a}}{ρ_{o}})}^{b - 1} = V_{o} {(0.97)}^{0.6 - 1} = V_{o} {0.97}^{- 0.4} = 1.01 V_{0} (12)

In section 3 the "dead time" error of the disdrometer has been analyzed. Realizing that the effort of applying the correction of the "dead time" error in all rain events is substantial and beyond the scope of this work and moreover the empirical equation cannot be applied in the bins that there aren't any counts at all, a simplifying assumption have been made: according to [15], which performed similar task in an intense storm, application of the dead time correction increased the estimated accumulation of rain for the entire event by almost 15%, mainly in the convective phase. The results of this previous work have been incorporated in the current, so "dead time" correction error is considered in the order of 15%, for all rain events.

A special problem encountered during the comparison process was about the synchronization among the Joss-Waldvogel disdrometer and the other two instruments in order to have comparable results (referring to the exact time period). Instruments b and c were synchronized as they refer to the same data logger, every 10 min. On the contrary the Joss-Waldvogel disdrometer has a more autonomous operation and the arranged time step has been set to 2 min. That resulted in occasionally slightly displaced data series. Apparent mistakes due to this problem have been corrected using logical criteria.

Finally another source of error in the disdrometer rainfall rate estimation comes from the adopted formulae of the terminal velocity that the disdrometer uses. For that reason four different empirical relationships of the raindrop terminal velocity were tested and the results of rainfall rate R were compared with the estimated results of the instruments' embedded formula. In Figure 1 the graphical representation of these relationships is shown for comparison reasons.

Figure 1: Four empirical relationships of terminal velocity.



Figure 1:  Four empirical relationships of terminal velocity.

Experimental Results - Comparison of Measured Data

According to the criteria referred to section 4, thirteen extreme rain events have been chosen among the time series of the recorded data. The date, time, average rain amount from the two rain gauges and the rain amount derived by the Joss-Waldvogel disdrometer are shown in Table 1. Also in the last column of Table 1 the percentage variation of the two sets is shown.

Table 1: Selection of extreme rainfall events.



  
    Episode 
    Date
    From
    To
    Rain amount (mm)^*
    Rain amount (mm)^**
    Variation%
  
  
    1
    17/11/2005
    7:40
    8:00
    16,8
    14,65
    -12,80
  
  
    2
    24/11/2005
    7:20
    7:40
    11,8
    9,93
    -15,82
  
  
    3
    5/2/2006
    23:30
    23:50
    14,7
    13,82
    -5,99
  
  
    4
    21/10/2007
    21:20
    21:40
    18,7
    16,04
    -14,21
  
  
    5
    12/6/2011
    12:50
    13:30
    34,9
    29,33
    -15,95
  
  
    6
    21/12/2011
    22:30
    22:50
    12,5
    10,18
    -18,59
  
  
    7
    6/2/2012
    18:30
    19:30
    34,0
    32,95
    -3,09
  
  
    8
    29/11/2012
    19:50
    20:20
    35,2
    24,26
    -31,09
  
  
    9
    16/1/2013
    9:50
    10:20
    17,8
    12,55
    -29,52
  
  
    10
    22/2/2013
    7:10
    7:30
    17,7
    10,30
    -41,83
  
  
    11
    22/2/2013
    9:40
    10:10
    21,6
    16,47
    -23,77
  
  
    12
    11/11/2013
    22:00
    22:20
    15,2
    11,69
    -23,12
  
  
    13
    25/1/2014
    0:10
    0:30
    36,6
    20,76
    -43,27
  
  
    Total
    
    350 min
    287,5
    222,91
    -22,47



Table 1:  Selection of extreme rainfall events.

As we can see in the last row of Table 1, the average difference between the conventional rain gauges and the Joss-Waldvogel disdrometer is -22.47%. That means that if the average shortcut due to "dead time" correction error is -15%, approximately an additional -7.5% is related to terminal velocity issues, or to the diameter limitations of the instrument. The terminal velocity issues, as mentioned, might be the altitude and air density variation (about 1% bigger velocities as estimated in section 4), break up and coalescence of rain drops, updraft or downdraft wind formations, atmospheric turbulence etc. Looking independently in each episode a wide variation of results is apparent that can't be depicted in the average value of variation. In episodes 3 and 7 the variation is very small, while in episodes 10 and 13 we have a very wide variation in the measured values. A detailed analysis about the nature of atmospheric factors responsible for these controversial results cannot be supported by specific scientific justification for each case. Moreover according to [15], velocity variations from the theoretical values don't follow a uniform pattern but it has been observed that in smaller diameters a percentage of drops tend to have higher than the theoretical, terminal speed (due to break up) and at higher diameters a percentage of drops tend to have smaller terminal speed (due to coalescence). On this experimental set up, there isn't the opportunity to verify this phenomenon, but the results indicate its existence.

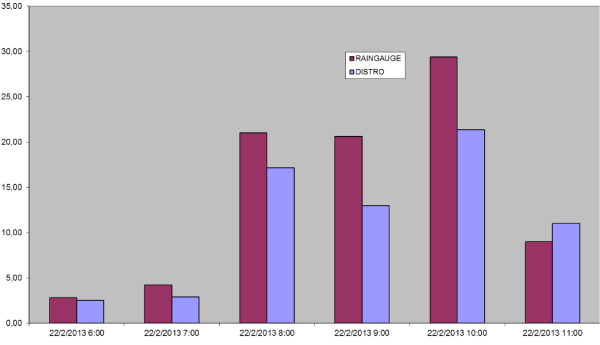
In Figure 2 a chart is plotted showing the events of 22/2/2013. These events were characteristic due to their catastrophic flooding consequences, especially in the eastern region of Attica. As we can see also in Table 1, disdrometer measurements underestimated the total rain amount by 41.83% (episode No 10) and 23, 77 % (episode No 11) respectively.

Download PDF

Citation: Baltas EA and Panagos DS. Sensitivity Analysis of the Error Contribution of Terminal Velocity of Drops, Using Joss-Waldvogel Disdrometer Data. Austin J Hydrol. 2014;1(2): 5. ISSN : 2380-0763

Instruction for Authors

Submit Your Article