Leontaritis AD; BaltasE

Review Article

Austin J Hydrol. 2014;1(2): 8.

Hydrological Analysis of the Aoos (Vjosë) -Voidomatis Hydrosystem in Greece

Leontaritis AD¹* and BaltasE²

¹Metsovion Interdisciplinary Research Center, National Technical University of Athens, Greece

²Department of Water Resources and Environment, Laboratory of Hydrology and Water Resources Management, National Technical University of Athens, Greece

*Corresponding author: Leontaritis AD, Laboratory of Steam Boilers and Thermal Plants, School of Mechanical Engineering, National Technical University of Athens, 9 Iroon Polytechniou, 15780 Zografou, Athens, Greece

Received: August 07, 2014; Accepted: September 31, 2014; Published: October 16, 2014

Abstract

The main goal of this work is to create a solid background for further study of the Aoos-Voidomatis hydro system. Aoos is the only upstream transboundary river of Greece, and together with its main tributary, Voidomatis, form a unique, protected ecosystem. Currently, there are no hydrological studies in the literature following the construction of the Aoos Springs dam in 1988, or any work to summarize its hydrological and geographical characteristics. This paper examines the extension and supplementation of available hydrological data in several measuring stations of the hydro system between 1950 and 2012. The original historical time-series dataset can be used for future studies, as primary data prior to and after the construction of the dam. Furthermore, this study provides a forecast for the monthly discharges of the river in the future, through the generation of a 50-year long synthetic time-series. As a result, the risk of failure to cover existing water needs was estimated. The methodology developed for the supplementation of the historical time-series, as well as, the creation of the synthetic time-series, includes some linear regression models and the forecasting autoregressive models (AR(1) and AR(2)). These models were applied to the available data with statistically significant results. The main conclusion that derived from this study is that current discharges can sufficiently cover the existing water needs; mainly for the irrigation of the Konitsa plain. However, it has been proven that the hydro system is sensitive to climate fluctuations and/or water use.

Keywords: Aoos; Vjosë; Voidomatis; Hydrological analysis; Autoregressive models; Water sufficiency

Introduction

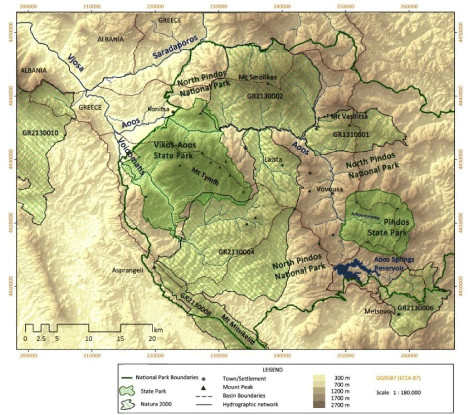
Aoos is a major Greek river belonging in the water district of Epirus and has a series of interesting characteristics that form the main reasons for its selection as a case study. It is the only upstream transboundary river of Greece [1], and even though there is no regulation between Greece and Albania regarding the water use from the Greek side of the border, its management remains an important issue. Its total catchment area covers 6519 km²; 67% or 4365 km² belongs to Albania while the remaining 33% or 2154 km² belongs to Greece; its discharge is estimated at 2154 hm3 on the Greek-Albanian borders, and at 5550 hm3 at its estuary in the Adriatic Sea [2]. As shown in Figure 1, Aoos and its main tributary, Voidomatis, form a unique, protected ecosystem (North Pindos National Park, Pindos State Park, Vikos-Aoos State Park, several Natura 2000 areas).

Figure 1: Map of Protected Areas.



Figure 1:  Map of Protected Areas.

The water district of Epirus has an area of 10026 km² and is located in the part of the country with the highest precipitation. It is characterized by a surplus of water balance and a low development rate. The mean annual rainfall ranges from 1000-1200 mm in coastal areas to 2000 mm in mountainous areas. The mean annual rainfall volume is estimated at 15878 hm3. The volume of surface runoff is 5523 hm³. The river basins with an area greater than 1000 km² are those of Aoos, Arachthos and Kalamas, covering about 58% of the total extent of the district. Aoos is a river of great hydrologic importance and flows towards the Albanian territory. The Arachthos River has the greatest length, 146 km. A percentage equal to 22% of the total extent of the district corresponds to watersheds with an area smaller than 40 km².

The relief and the geology of the wider area is diverse with extended mountainous regions, plateaus and low lands, affecting significantly the micro climate and the respective precipitation in each sub-basin, as well as its hydrological response throughout the year. Moreover, the hydrosystem has been affected by the Aoos Springs reservoir, as it will be analyzed next, while there are plans for further capitalizing from its high hydrodynamic potential. Currently, there is no work summarizing its hydrological and geographical characteristics or any hydrological study in the literature following the construction of the Aoos Springs dam in 1988. Therefore, any studies using the available hydrological data incorporate a significant error: the absence of the effect of the dam on the water flow of the river. Accordingly, the estimation of the water flow reduction in the different sections of the river after 1988 is of great importance, while on the other hand it constitutes a measure for the environmental impact of the dam. This work examines the extension and supplementation of available hydrological data in all the measuring stations of the hydrosystem for the period between 1950 and 2012. Furthermore, a forecast for the monthly water flow rates of the river in the future is provided through the generation of a 50-year long synthetic time-series using the autoregressive models AR(1) and AR(2) and the risk of failure to cover the existing water needs is estimated.

Data Acquisition

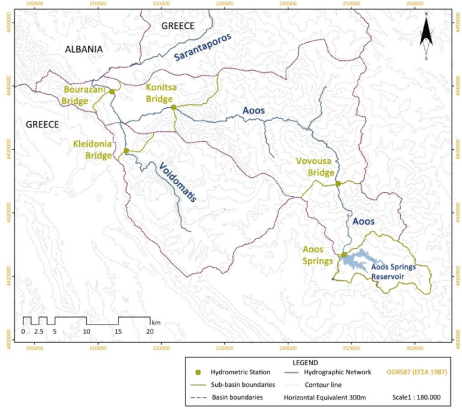
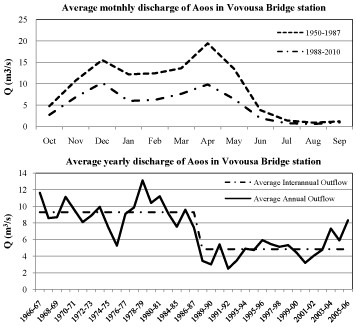
The hydrological data used in this study concern monthly water flow time series and were acquired from the archives of the Greek Public Power Corporation. The hydrosystem and the sites of the available hydrometric stations are presented in Figure 2. As already discussed, the construction of the Aoos Springs dam (hydrological year 1987-88) has significantly affected the hydrosystem as shown in Figure 3, which presents the discharge of Aoos in Vovousa Bridge, just a few kilometres downstream from the dam. Thus, the hydrological study has been divided into two periods: A) from hydrological year 1950-51 until 1986-87 and B) from 1988-1989 until 2011-2012. Hydrological year 1987-88 is not included in the study as a transient year between period A and B. It is noted that the water withheld in the reservoir is entirely diverted through the Aoos Springs Hydroelectric Plant to the basin of Arachthos hydrosystem and since there is no ecological discharge downstream from the dam, the sub-catchment area of the reservoir is abstracted in study period B.

Figure 2: Aoos-Voidomatishydrosystem and hydrometric stations.



Figure 2:  Aoos-Voidomatishydrosystem and hydrometric stations.

Table 1 summarises the catchment areas of all sub-basins for the two periods and Table 2 shows the respective average annual discharges according to the available data. At any case, the abstracted catchment area should not affect the qualitative response of the system. This is confirmed in Figure 3, where as it can be seen, the monthly response of the system follows a similar pattern in the two periods, suggesting a high reliability of the available hydrological data. Additionally, in Figure 3b the infamous drought of the early 90s as well as the wet period of 2003-2006 is clearly visible. However, the hydrometric stations did not operate continuously and as a result the historic time series for the two study periods (Table 3) are not complete and need to be supplemented. The methodology for the supplementation of the historic series as well as for the generation of the synthetic time-series is explained in the next paragraph.

Figure 3: Effect of the Aoos Springs dam (1988) on the a) Monthly discharge and b) Annual discharge of Aoos River in Vovousa Bridge (PPC, 2013).



Figure 3:  Effect of the Aoos Springs dam (1988) on the a) Monthly discharge and b) Annual discharge of Aoos River in Vovousa Bridge (PPC, 2013).

Table 1: Hydrometric stations and catchment area of their respective sub-basins prior to (?) and (?) after the construction of the Aoos Springs Reservoir.



  
    HYDROMETRIC STATIONS��� (Source: Public Power Corporation) 
  
  
    Site 
    Basin
    Catchment    AreaA (km²)
    Catchment    AreaB (km²)
  
  
    Aoos Springs
    Aoos
    79.1
    85.3
  
  
    Vovousa Bridge
    Aoos
    202.0
    116.7
  
  
    Konitsa Bridge
    Aoos
    665.0
    579.7
  
  
    Kleidonia Bridge
    Voidomatis
    332.0
    332.0
  
  
    Bourazani Bridge
    Aoos-Voidomatis
    1154.6
    1069.3



Table 1:  Hydrometric stations and catchment area of their respective sub-basins prior to (?) and (?) after the construction of the Aoos Springs Reservoir.

Table 2: Average annual discharge of the hydrometric station prior to (1967-77) and after (1991-2006) the construction of the Aoos Springs Reservoir.



  
    Average Annual Discharge 
  
  
    Hydrometric Station 
    Q_A (m³/s)
    Q_B (m³/s)
  
  
    Aoos Springs
    3.52
    3.30
  
  
    Vovousa Bridge
    9.23
    5.03
  
  
    Konitsa Bridge
    22.88
    N.A.
  
  
    Kleidonia Bridge
    14.88
    N.A
  
  
    Bourazani Bridge
    46.66
    N.A.



Table 2:  Average annual discharge of the hydrometric station prior to (1967-77) and after (1991-2006) the construction of the Aoos Springs Reservoir.

Table 3: Available Hydrological Data.



  
    Available Hydrological Data 
  
  
    Hydrometric Station 
    Hydrological Years 
  
  
    Aoos Springs
    1950-1987 and�    1991-2012
  
  
    Vovousa Bridge
    1966-1981 and 1983-2006
  
  
    Konitsa Bridge
    1963-1977
  
  
    Kleidonia Bridge
    1967-1977 
  
  
    Bourazani Bridge
    1973-1977 and 1979-1983



Table 3:  Available Hydrological Data.

Methodology and Tools

Supplementation of the historic time series

The basic elaboration of the available hydrological data concerned the identification of any outliers and, if necessary, their correction. The availability of measurements in different sections of the river enables the attribution of these outliers to flooding incidents or to errors. Errors can be induced both through the measuring procedure and through the elaboration of the initial hydrometric data (i.e. construction of stage-discharge curves). Having tracked any error-outlier value, it can be corrected with a simple linear regression model applied on the values of the flow in suitable hydrometric stations.

The supplementation of the missing data is also based on simple linear regression models. The most important aspect is the selection of suitable stations to apply the modelling procedure. First of all, the two stations should have available data for a sufficient common period. The other decisive parameter is the level of correlation between the two time-series for the common period (n), expressed by the correlation factor (r). The two time series are considered as suitable for the application of a simple linear regression model when

r \geq \frac{2}{\sqrt{n}}

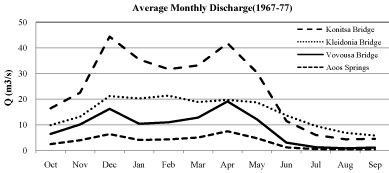
In various occasions, the supplementation of the data of a hydrometric station required different linear regression models with more than one hydrometric station (e.g. for the wet and for the dry period). Figure 4 shows a qualitative approach of the level of correlation between different hydrometric stations. The similarity of the curves of the different stations indicates a probable high correlation between them, which was confirmed by the calculation and analysis of the respective correlation factors. Naturally there were some deviations but overall the available data were sufficiently correlated for the complete supplementation of the historic time-series.

Figure 4: Average monthly discharge in different stations (1967-1977).



Figure 4:  Average monthly discharge in different stations (1967-1977).

Regarding period B, a slightly different approach is needed in order to take into consideration the effect of the dam. As it can be seen in Table 3, after 1987 there are available data only for the stations "Aoos Springs" (calculated from the reservoir water flow equilibrium) and "Vovousa Bridge". Since no measurements have been made in the rest of the stations for this whole period, no regression model can be directly applied for the supplementation of the missing data. In order to overcome this issue, the concept of the naturalised flow of the river was used. Practically the naturalised flow of the river is the theoretical natural flow of the river without the effect of the dam. Thus, the naturalised flow of the river for "Vovousa Bridge" station is calculated as the sum of the real flow at this point and the water flow withheld in the reservoir ("Aoos Springs" hydrometric station). Subsequently, these values can be used as input for the models used for period A and the naturalised monthly flow in all stations can be calculated for the whole period; the real flow is calculated by subtracting the respective monthly flow in "Aoos Springs" station. "Kleidonia Bridge" station is an exception as it is located on Voidomatis River and is not affected by the dam.

Generation of synthetic time-series - the autoregressive models AR(1) and AR(2)

In order to forecast the monthly water flow rates of the river in the future, it is necessary to create a synthetic time-series using a mathematical model. Since it is impossible to define all the parameters that influence physical quantities such as the water flow of a river, it is very difficult to describe their evolution with a deterministic model. On the other hand, their strong dependence on non-deterministic parameters (e.g. weather) makes possible their description over time through a stochastic model that can estimate the probability distribution of their values [3]. According to Hipel [4] in some cases of hydrological time series modelling a simple stochastic model may yield better results than a more complex deterministic model [5]. Stochastic models are used to generate synthetic hydrologic time series for the planning and management of water resource systems [6-9].

During the last few decades, several types of stochastic models have been developed and proposed [10-12] for modelling hydrological time series and generating synthetic stream flows [5]. These models are called system theoretic transfer function models because they attempt to establish a linkage between several phenomena without internal description of the physical processes involved [5]. Broadly, the stochastic models are classified as Autoregressive Moving Average (ARMA) models [13], disaggregation models [14], and models based on the concept of pattern recognition [15]. The forecast of the flow of rivers has been successfully achieved in several cases using linear models, such as AR, ARMAX, and Kalman filter [16-20].

For this study the autoregressive models AR (1) and AR (2) were selected. AR models incorporate solely auto regressive terms for modelling univariate time series [21]. They represent a time series Zt as a linear function of its previous values (Z_t-1,Z_t-2,....) and a random shock series (at, a_t-1, a_{t-2 ....}), an uncorrelated Gaussian random variable, with zero mean and constant variance [9]. The random shock series represent the stochastic error terms of the model and are assumed to be normally distributed random variables with zero mean and constant variance [21].

The AR(1) and AR(2) models have the following form:

Z_{t} = Φ_{1} \cdot Z_{t - 1} + a_{t} AR (1)

Z_{t} = Φ_{1} \cdot Z_{t - 1} + Φ_{2} \cdot Z_{t - 2} + a_{t} AR (2)

where Φ₁ and Φ₂ are the lag-one and lag-two autoregressive factors

According to Box and Jenkins [13] the development of an AR model requires at least a 50 event long time series but for strongly varying physical quantities this number should be even greater. In this case, the 62 year long supplemented historic time-series of monthly water flow will be used as an input to the models (see section 4.2), corresponding to a total of 62*12=644 events which can be considered as sufficiently long. Moreover, AR models can only be applied on stationary time-series and therefore the historic water flow time series need to be transformed accordingly. The conversion of the historic monthly discharge time-series to stationary is achieved through the following procedure: the monthly mean value is abstracted from each value and then it is divided by the respective standard deviation. This way any systematic variation of the values is abstracted and the stationary time-series contains only the stochastic part of the original historic time series. This procedure is expressed by the following equation:

x_{1} (i, j) = \frac{[X (i, j) - \bar{X} (j)]}{σ_{Z} (j)}

where

x₁(I,j) the monthly stationary value of discharge

X(I,j) the real historic monthly discharge

J the order of the month,

I the order of the year,

$\bar{X} (j)$ the real historic mean value of discharge for month j

$σ_{z} (j)$ the real standard deviation for month j.

Following the application of the auto regression models AR(1) and AR(2) two distinct 50 year long stationary synthetic time series of monthly discharges are created for each model. Therefore, the stationary synthetic time series need to be converted to "real" synthetic time-series following the opposite procedure to the one describe above. The stationary synthetic time series is divided into 12 classes (j) consisting of 50 values each that correspond to a single month. The classification can be done randomly as the time-series is stationary. Subsequently, the value i of each class j is converted using the equation:

X (i, j) = x_{1} (i, j) \cdot σ_{z} (j) + \bar{X} (j)

where

x₁(i,j) the synthetic stationary value of the monthly discharge

X(i,j) the "real" synthetic monthly discharge

j the order of the month (class)

i the order of the year

$\bar{X} (j)$ the real historic mean value of discharge for month j

$σ_{z} (j)$ the real standard deviation for month j.

Risk of failure

The N-year long synthetic time-series at a specific location of the river can be used to estimate the risk of non- adequacy for covering existing water needs like water supply, irrigation or hydroelectric power generation in the future [5]. Thus it is first necessary to exactly determine these needs at a monthly basis and then the risk can be estimated by using the following simple procedure:

The monthly discharge values Q (i,j) of the synthetic time series, where i denotes the order of the year, are sorted for each month j in descending order. The respective total monthly water needs are ? (j). Assuming for example month j, the cases for which Q (i,j)<A (j) are counted and m is the total number of these events. If N the length of the synthetic time series in years, then the possibility (risk) of not covering the water needs is calculated as:

P {Q (i, j) \leq A (j)} = \frac{m}{N + 1}

Results and Discussion

The supplemented historic time-series for the periods prior to and after the construction of the dam is summarized in Table 4. It is reminded that the naturalized flow of the river (Bn) is defined as the theoretical natural flow of the river without the effect of the dam. It is also noted that the discharge during period B is reduced compared to period A. This is due to two factors. Firstly, to the dam of Aoos Springs, which is particularly evident at all locations and especially at "Vovousa Bridge" and "Konitsa Bridge", where as expected the discharge in period B is significantly reduced. Secondly, this reduction is owed to reduced precipitation. This is confirmed by comparing average annual discharges during the two periods, at the locations that are not affected by the dam ("Aoos Springs", "Kleidonia Bridge"). The same conclusion can be drawn by comparing the average annual discharge for period A with the average naturalized annual discharge for period B, at the locations of "Vovousa Bridge", "Konitsa Bridge" and "Bourazani Bridge".In the latter station the difference of the discharge between the two periods is greater than in the other stations, which could be attributed to its larger catchment area. However, due to the limited availability of primary data for this station it needs to be investigated.

Table 4: Available Hydrological Data.



  
    Average monthly water flow for the period 1950-2012 (m³/s) 
  
  
    Station 
    Period 
    OCT
    ??V
    D?C
    JAN
    F??
    ??R
    ?PR
    ??Y
    JUN
    JUL
    ?UG
    S?P
    YEAR
  
  
    Aoos Springs
    A
    1.83
    3.96
    5.78
    4.88
    5.01
    5.32
    7.52
    5.27
    1.51
    0.52
    0.32
    0.43
    3.52
  
  
    B
    2.15
    4.96
    6.93
    4.24
    4.54
    6.06
    6.54
    3.03
    0.83
    0.39
    0.34
    0.70
    3.39
  
  
    Vovousa Bridge
    A
    4.77
    10.78
    15.54
    12.21
    12.44
    13.63
    19.44
    13.50
    3.84
    1.43
    0.92
    1.20
    9.12
  
  
    Bn^* 
    4.91
    11.84
    17.17
    10.22
    10.77
    13.71
    16.38
    9.48
    2.78
    1.17
    0.94
    1.67
    8.41
  
  
    
    B
    2.75
    6.88
    10.24
    5.98
    6.23
    7.65
    9.83
    6.44
    1.95
    0.79
    0.60
    0.97
    5.02
  
  
    Konitsa Bridge 
    A
    12.89
    22.45
    40.69
    31.27
    35.66
    34.98
    42.01
    33.31
    13.74
    5.95
    4.07
    4.49
    23.39
  
  
    Bn^* 
    13.13
    26.46
    46.78
    28.33
    31.29
    35.30
    35.98
    24.59
    10.76
    4.88
    4.33
    5.56
    22.24
  
  
    B
    11.00
    21.50
    39.85
    24.08
    26.75
    29.24
    29.44
    21.56
    9.93
    4.49
    3.99
    4.86
    18.85
  
  
    Kleidonia Bridge 
    A
    8.27
    13.15
    20.08
    21.29
    22.90
    20.68
    19.77
    19.82
    15.40
    9.01
    6.19
    5.58
    15.13
  
  
    B
    8.38
    15.20
    21.91
    20.19
    21.20
    20.84
    17.64
    16.60
    11.52
    7.03
    6.25
    6.62
    14.41
  
  
    Bourazani Bridge
    A
    22.80
    53.00
    64.26
    64.48
    60.58
    68.55
    72.43
    59.25
    30.71
    18.54
    13.52
    12.38
    44.95
  
  
    Bn^* 
    27.08
    53.08
    74.97
    58.11
    54.50
    63.78
    61.08
    44.21
    25.81
    15.66
    14.31
    14.16
    42.17
  
  
    B
    24.95
    48.12
    68.05
    53.87
    49.96
    57.72
    54.54
    41.17
    24.98
    15.28
    13.97
    13.46
    38.78
  
  
    (A=1950 - 1987, B =1988-2012, Bn^*= naturalized flow    for period B)



Table 4:  Available Hydrological Data.

A further analysis of the results in "Bourazani Bridge" not only provides their verification but also indicates the reliability of the used model. The "Bourazani Bridge" is located a few kilometers downstream of the confluence of Aoos and VoidomatisRiver, while the locations of "Konitsa Bridge" and "Kleidonia Bridge" are located at a short distance upstream from the above confluence, in Aoos and Voidomatis, respectively (Figure 2). The data verification consists of the following steps; firstly the sum of the annual discharge and basin area of "Kleidonia Bridge" and "Konitsa Bridge" are calculated for both periods A, B. Subsequently, the respective ratios "Bourazani Bridge"/Sum are calculated. The data and the results of the verification are given in Table 5. As shown in the table, these two ratios have about the same value for both periods A and B. This confirms the initial hypothesis that the greater discharge differences between the two periods in this location, in relation to other locations, is due to the greater basin area and not to model fault or wrong primary data. The above proportions remain the same for period B, during which there are no primary data at the above locations. This shows the precision of the simple linear regression model. It is noted that this procedure could be applied for these locations as the catchment area between the confluence of the two rivers and the location of "Bourazani Bridge" has similar characteristics with the rest catchment area of Aoos upstream from "Konitsa Bridge" and "Kleidonia Bridge": a combination of high mountains up to 2500m and semi-mountainous regions at an altitude ranging from 300 to 700m. However, this is not the case for the remaining locations due to the significantly heterogeneous characteristics of the basins. For example, the basin ratio for the locations of "Konitsa Bridge" and "Vovousa Bridge" is equal to 5.7, while the average ratio of annual discharge is equal to 3.5. The average annual rainfall in "Konitsa Bridge" (mixed catchment area) is about 1000mm, while in "Vovousa Bridge" (a purely mountainous catchment area)1400mm.

Table 5: Verification of the results at "Bourazani Bridge".



  
     
    Konitsa Bridge 
    Kleidonia Bridge 
    Sum
    Bourazani Bridge 
    Ratio 
      (Bourazani /Sum) 
  
  
    Basin A (km²)
    665.0
    332.0
    997.0
    1154.6
    1.158
  
  
    Basin B (km²)
    579.7
    332.0
    911.7
    1069.3
    1.173
  
  
    Discharge A (m³/s)
    23.39
    15.13
    38.52
    44.95
    1.167
  
  
    Discharge B (m³/s)
    18.85
    14.41
    33.26
    38.78
    1.166



Table 5:  Verification of the results at "Bourazani Bridge".

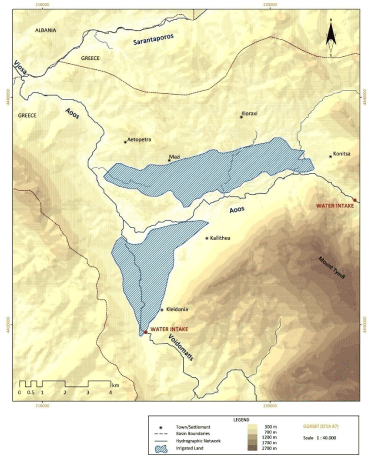
Irrigation needs and water availability

The main water needs that are covered by Aoos and Voidomatis concern the irrigation of the plains of Konitsa (11500 hectares irrigated by Aoos River) and Kleidonia (4500 hectares irrigated by Voidomatis River). The water intake takes place upflow from "Konitsa Bridge" and "Kleidonia Bridge" respectively (Figure 5). Other water uses include the water supply of several minor villages through small streams and springs of the wider basin. The overall quantities are practically insignificant and are therefore neglected in this study. The monthly needs in irrigation water for the two plains have been estimated in the study for the construction of the new irrigation system of the greater Konitsa area [22]. Table 6 summarizes the irrigation monthly needs (May-September) and the respective average available discharges as well as the standard deviation for the two locations as calculated in the first part of this study. For "Kleidonia Bridge" that is not affected by the dam the discharge refers to the whole study period (1950-2012) while for "Konitsa Bridge" only to period B (1988-2012).

Figure 5: Map of irrigated areas in the Konitsa-Kleidonia Plain.



Figure 5:  Map of irrigated areas in the Konitsa-Kleidonia Plain.

Table 6: Irrigation Needs and Water Availability at "Konitsa Bridge" (1988-2012) and "Kleidonia Bridge" (1950-2012).



  
    Irrigation Needs and Water    Availability
  
  
     
    (m3/s)
    May
    June
    July
    August
    September
  
  
    Konitsa Bridge
    Irrigation
    0.381
    0.590
    0.700
    0.610
    0.400
  
  
    Discharge
    21.56
    9.93
    4.49
    3.99
    4.86
  
  
    S.D.
    7.38
    3.26
    0.92
    1.17
    2.97
  
  
    Kleidonia Bridge
    Irrigation
    0.149
    0.232
    0.273
    0.238
    0.155
  
  
    Discharge
    18.97
    13.80
    8.69
    6.66
    6.23
  
  
    S.D
    4.34
    4.34
    2.75
    2.03
    3.20



Table 6:  Irrigation Needs and Water Availability at "Konitsa Bridge" (1988-2012) and "Kleidonia Bridge" (1950-2012).

In "Kleidonia Bridge" the water needs are low compared to the discharge of Voidomatis River and thus there is practically no risk of failure and no further studying is needed. However, in "Konitsa Bridge" during July, August and September the irrigation needs are greater, and the discharge of Aoos combined with the relatively high standard deviation indicate a possibility of failure, which will be further studied next.

Synthetic time series

For the reasons explained in the above paragraph the synthetic time-series will be created only for "Konitsa Bridge". However, since the forecast models refer to future discharges of the river the effect of the dam should be taken into consideration and thus the historic time series needs to be modified in order to be entirely used as an input for the models: all discharge values for period a need to be deducted to period B (denaturalised flow). This is achieved simply by abstracting the discharge in "Aoos Springs" from the respective value in "Konitsa Bridge". The result is a 62 year long hypothetic historic denaturalised monthly discharge time-series in "Konitsa Bridge" (Table 7) as if the dam existed since 1950.

Table 7: Historic denaturalized monthly discharge time-series at "Konitsa Bridge" (1950-2012).



  
    Historic denaturalised monthly    discharge time-series in "Konitsa Bridge" (1950-2012) 
  
  
    
    OCT
    NOV
    DEC
    JAN
    FEB
    MAR
    APR
    MAY 
    JUN
    JUL
    AUG
    SEP
    YEAR
  
  
    Q (m³/s) 
    11.02
    20.14
    37.60
    25.14
    28.52
    29.43
    31.73
    24.51
    10.98
    4.92
    3.88
    4.49
    19.32
  
  
    σ (m³/s)
    9.20
    13.13
    22.44
    9.90
    11.50
    11.89
    9.45
    9.25
    3.77
    1.27
    0.97
    2.30
    4.19



Table 7:  Historic denaturalized monthly discharge time-series at "Konitsa Bridge" (1950-2012).

The results of the synthetic-series calculations are summarized in Table 8. It is noted, that as expected, the average monthly discharges as well as the respective standard deviations are similar to the values of the historic time series for both models and thus there is no need to use higher class (>2) AR models.

Table 8: Results of the synthetic time-series calculationsat "Konitsa Bridge" using the forecast models AR(1) and AR(2).



  
    Results of Synthetic Time-Series 
  
  
    
    OCT
    NOV
    DEC
    JAN
    FEB
    MAR
    APR
    MAY
    JUN
    JUL
    AUG
    SEP
  
  
    Historic time-series 
  
  
    � $\bar{X}$ (m³/s) 
    11.02
    20.14
    37.60
    25.14
    28.52
    29.43
    31.73
    24.51
    10.98
    4.92
    3.88
    4.49
  
  
    s (m³/s)
    9.20
    13.13
    22.44
    9.90
    11.50
    11.89
    9.45
    9.25
    3.77
    1.27
    0.97
    2.30
  
  
    AR(1) 
    
    
    
    
    
    
    
    
    
    
    
    
  
  
    � $\bar{X}$ (m³/s)
    10.87
    23.16
    34.95
    25.84
    27.54
    31.27
    34.16
    24.69
    10.87
    4.94
    4.20
    4.67
  
  
    s (m³/s)
    9.12
    13.21
    21.77
    8.58
    12.29
    13.04
    8.32
    9.23
    3.59
    1.21
    0.94
    2.02
  
  
    AR(2) 
    
    
    
    
    
    
    
    
    
    
    
    
  
  
    � $\bar{X}$ (m³/s) 
    10.51
    21.32
    33.67
    25.25
    27.86
    29.00
    31.09
    26.61
    11.86
    4.52
    3.77
    4.57
  
  
    s (m³/s)
    7.55
    12.89
    21.08
    8.64
    11.37
    12.40
    8.60
    10.22
    4.20
    1.34
    1.11
    1.85



Table 8:  Results of the synthetic time-series calculationsat "Konitsa Bridge" using the forecast models AR(1) and AR(2).

Risk of failure

Following the generation of the synthetic time series of monthly discharges, the risk of non-adequacy for covering irrigation needs at "Konitsa Bridge" was calculated using the procedure described in section 3.3. The procedure was applied only for the months of July, August and September for the reasons analyzed above. The results of the procedure for the two synthetic time series are shown in Table 9.

Table 9: Results of risk calculation.



  
    Risk calculation procedure (m³/s) 
  
  
     
    AR(1)
    AR(2)
  
  
    YEAR 
    JUL
    AUG
    SEPT
    JUL
    AUG
    SEPT
  
  
    Irrigation 
    0.70
    0.61
    0.40
    0.70
    0.61
    0.40
  
  
    1 
    7.54
    6.46
    8.51
    8.74
    6.11
    8.49
  
  
    2 
    7.14
    6.17
    8.19
    7.00
    5.93
    7.93
  
  
    3 
    6.99
    5.67
    7.57
    6.52
    5.67
    7.53
  
  
    4 
    6.62
    5.59
    7.50
    6.51
    5.14
    7.49
  
  
    5 
    6.42
    5.28
    7.37
    6.25
    5.01
    7.36
  
  
    6 
    6.37
    5.11
    7.34
    6.10
    4.88
    7.20
  
  
    7 
    6.27
    5.05
    7.16
    6.05
    4.87
    7.05
  
  
    8 
    6.26
    4.99
    6.98
    5.96
    4.79
    6.48
  
  
    9 
    6.20
    4.95
    6.95
    5.86
    4.79
    6.10
  
  
    10 
    6.13
    4.92
    6.81
    5.71
    4.69
    6.02
  
  
    � 
     
     
     
     
     
     
  
  
    41 
    3.87
    3.51
    2.62
    3.55
    2.77
    2.96
  
  
    42 
    3.75
    3.50
    2.55
    3.45
    2.75
    2.83
  
  
    43 
    3.71
    3.42
    2.52
    3.36
    2.71
    2.70
  
  
    44 
    3.65
    3.38
    2.50
    3.34
    2.70
    2.36
  
  
    45 
    3.61
    3.16
    2.24
    3.09
    2.57
    1.92
  
  
    46 
    3.53
    2.92
    2.22
    3.07
    2.13
    1.85
  
  
    47 
    3.36
    2.91
    2.16
    2.85
    2.06
    1.84
  
  
    48 
    3.26
    2.69
    1.46
    2.62
    1.85
    1.74
  
  
    49 
    2.40
    2.17
    1.04
    1.70
    1.50
    0.77
  
  
    50 
    1.77
    1.19
    0.27
    1.20
    0.62
    0.12
  
  
     $P = \frac{m}{N + 1} = \frac{1}{51} = 1.96 %$



Table 9:  Results of risk calculation.

A miss is observed in September, once in 50 years, in both synthetic time series. This corresponds to a 1.96% risk. At this point it is important to emphasize that special care is required when interpreting these results. It is reminded that irrigation water is abstracted through technical work at a location about 1 km upstream of the hydrometric station of "Konitsa Bridge" (Figure 4). However, there are no quantitative data regarding this irrigation project. Its operation began before 1963, when the first measurements were taken, and therefore its effect on monthly discharges during the irrigation period is incorporated in the available measurements. In any case, the irrigation needs are fully covered by this project to date. Additionally, the construction of a new modern project is scheduled for the irrigation of the entire area of Konitsa from the rivers Aoos and Voidomatis. The water transfer will be more efficient, reducing the total losses and therefore the water amount that is needed. Thus, the risk should be redefined qualitatively.

As shown in the table of results, beyond the failure value in both synthetic time series, the values are significantly above the threshold for irrigation needs. This fact, in combination with those mentioned above, make the risk practically zero on a monthly basis. If the simulated discharge values were zero or negative then the interpretation of the calculated risk would be different. Negative discharges have apparently no physical meaning and would be replaced by zero. Their statistical significance, however, is that the curve of the probability distribution function would be shifted closer to the limit point for the cover of irrigation needs. The failures that would be identified in that case would be statistically significant and so the risk.

It is also reported that if the analysis was on a weekly or daily basis, the risk would be greater. This means that there may be a weakness to cover the needs for a short time during the period July-August. Even if this time period is two or three days, it would be a problem for sensitive crops, such as alfalfa that is common in the Konitsa plain.

In summary, based on the above analysis there is no risk of insufficiency of the water amount at the location of "Konitsa Bridge" to meet the irrigation needs of the Konitsa plain, but the hydrosystem proved to be sensitive during the summer months. Moreover, as it was shown in the study of Mimikou et al. [23], changes in the hydrological regime of north western Greece due to the climate change include the reduction of the summer runoff values in all studied cases and basins considering various climate change scenarios. Therefore, the Aoos river water system is vulnerable during the dry summer period and changes in climate or water use can cause its imbalance.

Conclusion

The main goal of this work was to create a solid background for the further study of the Aoos-Voidomatis hydrosystem. Initially the available hydrological data from several hydrometric stations were supplemented and extended for the period 1950-2012, using simple linear regression models with significant precision. The original historical time-series data set created can be used in future studies as primary data prior to and after the construction of the Aoos Springs dam.

Furthermore, the monthly water flow rates of the river were forecasted through the generation of a 50-year long synthetic time-series with the use of the autoregressive models AR(1) and AR(2) based on its historical discharge values and thus without taking into consideration any climatic changes. These models were applied to the available data with statistically significant results. Subsequently the risk of failure to cover existing water needs was estimated. The analysis of the results showed that current water flow rates can sufficiently cover the existing water needs; mainly for the irrigation of the Konitsa plain, with practically no risk of failure. However, it was proven that the hydrosystem is sensitive to climate fluctuations and/or water use, especially during the summer months and thus it requires a long-term sustainable management plan.

References

Download PDF

Citation: Leontaritis AD and BaltasE. Hydrological Analysis of the Aoos (Vjosë) -Voidomatis Hydrosystem in Greece. Austin J Hydrol. 2014;1(2): 8. ISSN : 2380-0763

Instruction for Authors

Submit Your Article

Available Hydrological Data
Hydrometric Station	Hydrological Years
Aoos Springs	1950-1987 and� 1991-2012
Vovousa Bridge	1966-1981 and 1983-2006
Konitsa Bridge	1963-1977
Kleidonia Bridge	1967-1977
Bourazani Bridge	1973-1977 and 1979-1983