How Sensitive is Mass-Based Inverse Optimization to IMRT Delivery Parameters?

Research Article

Austin J Med Oncol. 2021; 8(2): 1064.

How Sensitive is Mass-Based Inverse Optimization to IMRT Delivery Parameters?

De Ornelas M and Mihaylov IB*

Department of Radiation Oncology, University of Miami Miller School of Medicine, Sylvester Comprehensive Cancer Center, Miami, Florida

*Corresponding author: Ivaylo B Mihaylov, Department of Radiation Oncology, University of Miami Miller School of Medicine, Sylvester Comprehensive Cancer Center, 1475 NW 12th Avenue, Suite 1500, Miami, FL 33136, Florida

Received: May 18, 2021; Accepted: June 16, 2021; Published: June 23, 2021

Abstract

Purpose: To determine the sensitivity of changes to IMRT delivery parameters for mass-based optimization schemes: Dose-Mass- (DM) and Energy-based (Energy), compared to Dose-Volume-based (DV) optimization.

Methods: Twelve Head-and-Neck (HN) and twelve lung cases were retrospectively optimized using DM and Energy optimization. In both optimization approaches nine equidistant, split beams were used for step-and-shoot deliverable IMRT. Changes to two parameters were investigated: the number of IMRT segments (5 and 10 per beam) and the minimum allowed segment area (2 and 6 cm²). Plans were normalized such that 95% of the PTV received the same dose. Dose Indices (DIs) were used for evaluation. For the lung cases, DIs included: 1%_cord, 33%_heart, 20% and 30%_both-lungs, and 50%_ esophagus. In the HN cases: 1%_cord, 1%_brainstem, left/right parotids_50%, 50%_larynx, and 50%_esophagus.

Results: The lung cases demonstrated that the Energy plans were more sensitive to segment area; changing the segment area resulted in a statistically significant dose increase for 1%_cord, 30%_both-lungs and 50%_esophagus. Changes to the number of segments yielded on average statistically significant differences in dose to 1%_cord in Energy plans, 50%_esophagus in DM plans, and 20%_both-lungs in DV plans. When the segment area was changed, the HN cases yielded statistically significant differences in doses to 1%_cord, 1%_ brainstem, 50%_left and right parotids, and 50%_larynx for the Energy plans and 50%_larynx for DM plans. Moreover, changing the number of segments resulted in significant dose decrease for 50%_parotids and 50%_esophagus for the Energy plans and 50%_larynx for DV plans.

Conclusions: This study showed that both lung and HN Energy plans exhibit larger sensitivity than DV and DM plans to changing IMRT delivery parameters, especially when increasing the minimum segment area rather than with varying the number of segments.

Keywords: Mass; Energy; IMRT; Inverse optimization; DMPO

Introduction

Inverse optimization for IMRT planning can be performed in either one- or two-step process. In the two-step process fluence optimization is performed first and leaf trajectories are generated afterwards [1,2]. In the more recent one-step approach the Multi-Leaf Collimator (MLC) leaf-sequencing step and other physical constraint parameters are included in the optimization in order to generate deliverable plans. One-step optimization can be performed by Direct Aperture Optimization (DAO), which uses simulated annealing algorithm, or Direct Machine Parameter Optimization (DMPO) using gradient descent algorithm [3]. This type of optimization reduces the number of segments and monitor units, and in addition improves conformity and homogeneity without compromising plan quality [1,4,5]. Studies have demonstrated that the different IMRT parameters defined prior to optimization, such as the number of segments, segment area, number of intensity levels, number of MUs per beam, and MLC leaf increment affect plan outcome [6-10].

Dose-Mass-based (DM) optimization has been shown to be a more general form of Dose-Volume-based (DV) optimization, which is the special case where medium density is constant [11]. Another optimization approach that has been suggested is based on integral dose [12], in which the objective is to minimize the total energy imparted to the Organs-At-Risk (OARs). This optimization scheme also uses density information to obtain the energy deposited, referred herein as Energy-based optimization (Energy). The aim of this work is to investigate the sensitivity of density-based optimization approaches: DMH and Energy to DMPO parameter variations.

Methods and Materials

Twelve lung and twelve Head-and-Neck (HN) patients were retrospectively optimized using, DV, DM and Energy optimization. The plans were generated with nine equidistant coplanar beams with a minimum of 7 MUs per segment. The number of beams, beam angles, and minimum MUs per segment were set the same for all plans. Changes to two parameters were investigated: the maximum number of IMRT segments (5 and 10 per beam) and the minimum allowed segment area (2 and 6 cm²). Therefore, four plans were developed for each approach: 5s_2a, 5s_6a, 10s_2a and 10s_6a, the nomenclature used refers to the combination of number of segments per beam (i.e. 5s: 5 segments/beam) and the minimum segment area of (i.e. 2a: 2 cm2). Optimization was performed with Pinnacle V.8.1y (Philips Radiation Oncology Systems, Fitchburg, WI) with DMPO (Direct Machine Parameter Optimization). Dose grid was 3 mm for the HN cases and 4 mm for the lung cases. During optimization the dose to Organs At Risk (OARs) was iteratively lowered through automated inverse optimization [13] until the standard deviation of the dose across the PTV was between approximately 4%. All plans were normalized so that 95% of the PTV received the prescription dose. Prescription dose for the lung cases was 70 Gy in 35 fractions and 66 Gy in 33 fractions for the HN cases. The sensitivity metric used in this study was based on Dose Indices (DIs), which represent the dose delivered to a certain anatomical structure volume. The DIs used for plan assessment included: 1%_cord, 33%_heart, 20% and 30%_both-lungs, and 50%_esophagus for the lung cases. For the HN cases: 1%_cord, 1%_brainstem, 50%_left/right parotids, 50%_larynx, and 50%_esophagus. The sensitivity of the plans due to the changes in parameters were assessed using a paired two-tailed paired student’s t-test. The average values of the DIs were deemed to be statistically different if p-value was less than 0.05.

Results

The lung cases resulted in larger changes observed with Energy plans compared to DM plans. According to DV-based studies 10 segments per beam and a minimum segment area of about 5 cm2 are appropriate for lung cases [14]. In order to compare the resultant plans with what would be clinically applied, Figure 1 illustrates the average dose per DI for each parameter combination with respect to 10 segments per beam and 6 cm² segments area for comparison purposes, since they are the closest to clinically suitable parameters. When increasing the segment area and keeping 5 segments per beam, the Energy plans showed statistically significant increase in dose to 1%_cord, 30%_both-lungs and 50%_esophagus. The Energy plans also resulted in statistically significant changes to maximum dose to cord using 10 segments per beam and increasing the segment area. Moreover, for dose to 1%_cord, increasing the number of segments using 6 cm² segment area was statistically significant. DM plans resulted in significant differences only when the segment area increased for 50%_esophagus with 10 segments per beam. The DV plans resulted in statistically significant differences for 20%_bothlungs when increasing the segments using 6 cm² area. No statistically significant changes were observed with changing segment area for DV and DM plans.

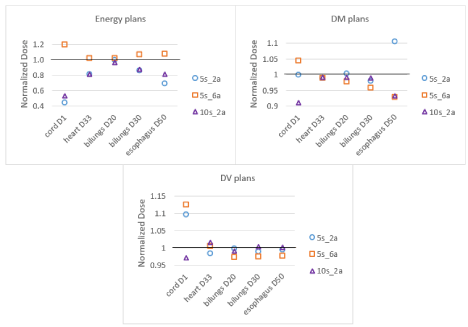
Figure 1: Lung cases: Each point represents the mean dose (for the patient cohort) normalized of the parameter combination (i.e., 5s_6a is 5 segments/beam with 6 cm² area) with respect to 10 segments/beam with 6 cm2 as it is the most closely resembling the clinically used DMPO segment parameters in DV optimization. It is important to note the differences in the ordinate scale as the Energy plans showed significantly larger variation in values with a range of [0.45-1.20].

    

    
    

    

    Figure 1: Lung cases: Each point represents the mean dose (for the patient cohort) normalized of the parameter combination (i.e., 5s_6a is 5 segments/beam with
6 cm² area) with respect to 10 segments/beam with 6 cm2 as it is the most closely resembling the clinically used DMPO segment parameters in DV optimization. It
is important to note the differences in the ordinate scale as the Energy plans showed significantly larger variation in values with a range of [0.45-1.20].

The HN cases also showed larger changes with the Energy plans (cf. Figure 2). The values shown in Figure 2 are with respect to 10 segments/beam and 2 cm² minimum segment area in order to visually illustrate the dose variation in comparison to what is clinically suitable. Results showed statistically significant differences in dose when increasing the segment area for 1%_brainstem, 50%_left and right parotids and 50%_larynx using either number of segments per beam (5 and 10 segments/beam). Also dose to 1%_cord, was on average statistically significant when increasing the segment area with 10 segments per beam. Furthermore, increasing the number of segments using 2 cm² segment area, resulted in significant dose decrease for 50%_parotids and 50%_esophagus. The DV plans showed statistically significant dose increase when changing the number of segments from 5 to 10 for 50% larynx, and using either segment area. In addition, dose to esophagus_50% resulted in significant difference when using 6 cm² segment area and increasing the number of segments. Remarkably, the only DI that showed significant difference in the DM plans was 50%_larynx when increasing the segment area with 10 segments/beam.

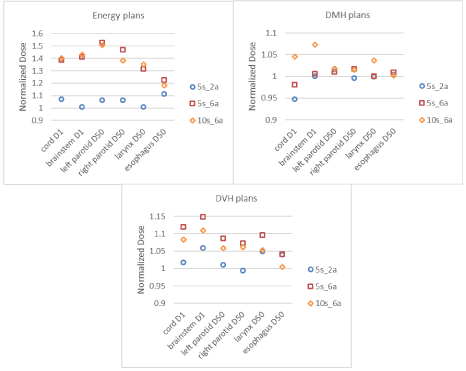
Figure 2: HN cases: Each point represents the mean dose (for the patient cohort) normalized to the parameter combination (i.e. 5s_2a is 5 segments/beam with 2 cm² area) with respect to 10 segments/beam with 2 cm² as it is the parameters most closely resembling the clinically used DMPO segment parameters in DV optimization. It is important to note the differences in the ordinate scale as the Energy plans showed significantly larger variation in values (range: [1-1.51]) compared to DMH (range: [0.95-1.07]).

    

    
    

    

    Figure 2: HN cases: Each point represents the mean dose (for the patient cohort) normalized to the parameter combination (i.e. 5s_2a is 5 segments/beam
with 2 cm² area) with respect to 10 segments/beam with 2 cm² as it is the parameters most closely resembling the clinically used DMPO segment parameters in
DV optimization. It is important to note the differences in the ordinate scale as the Energy plans showed significantly larger variation in values (range: [1-1.51])
compared to DMH (range: [0.95-1.07]).

Discussion

In this work, the sensitivity to changes in two IMRT parameters: minimum segment area and number of segments were investigated. In DV optimized plans, segment parameters have shown to change plan quality. A previously published study concluded that complex plans benefit from large number of segments and small areas [8]. The mentioned study showed that a range between 80-120 number of segments and a segment area of 4-8 cm² was appropriate for complex HN cases but decreasing the number of segments and increasing segment area for more simple cases showed good plan quality. Another study suggested that limiting the minimum segment area to less than 5 cm2 kept the dose to OARs and PTVs within desired limits and dose deviations within 4% for HN cases [6]. For lung cases, it has been demonstrated that with a maximum of 40 segments in total with five fields the dose homogeneity would not be compromised [14]. It is important to note that highly modulated plans with very small segment areas may not be deliverable due to hardware limitations [15,16]. Dosimetric differences between planned and measured dose can be attributed to dose calculation errors in the treatment planning system, errors by the dosimeter used, and errors of the linac [16]. Errors of the linac include errors due to mechanical limitations of the MLCs, which typically occur with very complex and highly modulated plans.

In line with the mentioned DV studies, in the DM and Energy plans the segment area smaller than 5 cm2 and number of segments greater than 80 was beneficial for HN cases for most DIs. However, the average maximum dose to the cord showed better sparing with 5 segments per beam for the DM plans. The results for the DV plans were in line with previously published studies, where the 10s_2a parameter combination showed the lowest average doses for all DIs and the doses increased with larger segment area and less segments per beam. Similar to those results were the results for the Energy DIs, but the changes were larger as the segment area increased. In somewhat simpler lung anatomy, the number of segments can be smaller, and the allowed segment area could be larger for clinically viable solutions. The results for improving dose sparing with a certain combination was not uniform across DIs for the DV plans, but the dose changes were small when varying the parameters. The Energy plans showed that a segment area of 2 cm2 improved most DIs, regardless of the number of segments. These results show that with the use of a single objective function, as is Energy optimization, any variation of IMRT segment parameters changes the plan more drastically than in multi objective optimization approaches such as DV and DM. Therefore, it is important to appropriately determine the DMPO parameters for Energy optimization.

Conclusion

Energy optimization showed more sensitivity to IMRT segment parameter variations compared to DV and DM optimization. The sensitivity was more notable in the HN rather than in the lung cases, which may be due to the close proximity of many OARs in the HN anatomy. The Energy plans were more sensitive to the segment area than to the number of segments per beam.

Acknowledgment

This work is supported by R01 CA163370.

References

  1. Hårdemark BL, Rehbinder A, Löf H, Johan P. Direct machine parameter optimization. Phillips Medical Systems. 2003.
  2. Shepard DM, Earl MA, Li XA, Naqvi S, Yu C. Direct aperture optimization: a turnkey solution for step-and-shoot IMRT. Medical Physics. 2002; 29: 1007- 1018.
  3. Li Y, Sun X, Wang QI, et al. A feedback constraint optimization method for intensity-modulated radiation therapy of nasopharyngeal carcinoma. Oncology letters. 2015; 10: 2043-2050.
  4. Dobler B, Koelbl O, Bogner L, Pohl F. Direct machine parameter optimization for intensity modulated radiation therapy (IMRT) of oropharyngeal cancer – a planning study. Journal of Applied Clinical Medical Physics. 2009; 10: 4-15.
  5. Ludlum E, Xia P. Comparison of IMRT planning with two-step and one-step optimization: a way to simplify IMRT. Physics in Medicine and Biology. 2008; 53: 807-821.
  6. Mittauer K, Lu B, Yan G, et al. A study of IMRT planning parameters on planning efficiency, delivery efficiency, and plan quality. Medical Physics. 2013; 40: 061704.
  7. Derbyshire SJ, Morgan AM, Thompson RCA, Henry AM, Thwaites DI. Optimal planning parameters for simultaneous boost IMRT treatment of prostate cancer using a Beam Modulator™. Reports of Practical Oncology and Radiotherapy. 2009; 14: 205-213.
  8. Cheong K-H, Kang S-K, Lee M, et al. Analytic study on the effects of the number of MLC segments and the least segment area on step-and-shoot head-and-neck IMRT planning using direct machine parameter optimization. Journal of the Korean Physical Society. 2013; 62: 1330-1339.
  9. Worthy D, Wu Q. Parameter optimization in HN-IMRT for Elekta linacs. Journal of Applied Clinical Medical Physics. 2009; 10: 43-61.
  10. Jiang Z, Earl MA, Zhang GW, Yu CX, Shepard DM. An examination of the number of required apertures for step-and-shoot IMRT. Physics in Medicine and Biology. 2005; 50: 5653-5663.
  11. Mihaylov IB, Moros EG. Mathematical Formulation of DMH-Based Inverse Optimization. Frontiers in Oncology. 2014; 4: 331.
  12. Mihaylov IB. Mathematical formulation of energy minimization – based inverse optimization. Frontiers in Oncology. 2014; 4: 181.
  13. Mihaylov IB, Mellon EA, Yechieli R, Portelance L. Automated inverse optimization facilitates lower doses to normal tissue in pancreatic stereotactic body radiotherapy. PLOS ONE. 2018; 13: e0191036.
  14. Nioutsikou E, Bedford JL, Christian JA, Brada M, Webb S. Segmentation of IMRT plans for radical lung radiotherapy delivery with the step-and-shoot technique. Medical Physics. 2004; 31: 892-901.
  15. McNiven AL, Sharpe MB, Purdie TG. A new metric for assessing IMRT modulation complexity and plan deliverability. Medical Physics. 2010; 37: 505-515.
  16. Li JG, Dempsey JF, Ding L, Liu C, Palta JR. Validation of dynamic MLCcontroller log files using a two-dimensional diode array. Medical Physics. 2003; 30: 799-805.

Citation: De Ornelas M and Mihaylov IB. How Sensitive is Mass-Based Inverse Optimization to IMRT Delivery Parameters?. Austin J Med Oncol. 2021; 8(2): 1064.