Application of Deep Learning LSTM and ARIMA Models in Time Series Forecasting: A Methods Case Study analyzing Canadian and Swedish Indoor Air Pollution Data

Research Article

Austin J Med Oncol. 2022; 9(1): 1073.

Application of Deep Learning LSTM and ARIMA Models in Time Series Forecasting: A Methods Case Study analyzing Canadian and Swedish Indoor Air Pollution Data

*Corresponding author: Selim Muhammad Khan Cumming School of Medicine, University of Calgary, Canada

Received: November 05, 2022; Accepted: December 22, 2022; Published: December 28, 2022

Abstract

Time series analysis and forecast are vital to understand how a public health hazard evolves over time and what are its influencing factors; these also generate evidence for preventive actions to avoid the potential consequences. There have been a lot of traditional time series analysis methods used in research. The new generation deep learning LSTM (long Short-Term Memory) time series analysis model is promising as it can prevent memory loss that vanishes and explodes the gradient in neural network, deal with enormous volume of data and produce more precise nonlinear forecasts from multivariate inputs whereas the traditional (S)ARIMA (seasonal autoregressive integrated moving average) models that can predict linearly from a single variable. As the health hazard from the soil gas radon is multifactorial and current measures are proved ineffective and death toll from the risk is increasing, we applied this new method to analyze pilot data gathered in Canada through the Evict radon research consortium and got comparable ones from Sweden through Radonova. We conducted both deep learning LSTM and traditional (S)ARIMA modeling using Python-Jupyter notebook and the econometric toolset of MATLAB 2020b. We identified the trends and seasonalities, filtered and trained data, and fitted into the LSTM and (S)ARIMA models; then, forecasted radon levels for the two countries till 2100 AD. We compared and contrasted two models to provide clear ideas to the emerging researchers about the benefits and constraints of both. This methods case study has implications for modelled prediction from big time series data, not limited to the public health risk from indoor air pollution.

Keywords: Time Series Analysis; Deep learning; Long Short- Term Memory; (S)ARIMA; Indoor Air Pollution; Radon Health Risk; Prediction

Highlights

• We applied the next generation deep learning LSTM model for time series forecasting of indoor radon health risk and compared its performance to the traditional ARIMA/SARIMA models.

• Presented the model codes and parameters along with the extra benefits of the cutting-edge deep learning LSTM model over the traditional ones.

• Analytics skills in building and employing advanced models to forecast from big time series data can facilitate research, not lim-ited to the health risk from indoor air pollution.

Learning Outcomes

By the end of this methods case, student researchers should be able to

• Understand and describe the building, training and application of deep neural networks (LSTM model) and ARIMA/SARIMA models to the time series data of any context for risk analysis and prediction.

• Compare and contrast the strengths and weaknesses of these two different analytic tools.

• Experiment and appraise the outcomes generated by these tools to be able to decide on their usage.

Introduction

Time series is a sequence where one or multiple metrics are recorded as data point over regular periodic intervals. With the huge production of high dimensional data, the utility of and interest in time series analysis is increasing day by day. Depending on the frequency, a time series can be annual (annual incidence of a disease, exposure to a risk factor), quarterly (patient turnover or expenses of a hospital), monthly (emergency caseloads, patient admission), weekly (number of deliveries, patient discharges, daily (infectious covid-19 cases, recovery), hourly (visitor’s traffic, outdoor consultation), minutes (inbound calls in emergency room) and even seconds wise (Twitter trends, web traffic). [1,6,9,15,16]. By analyzing such continued time series data, we can forecast what the future values of the series will be. Such time series forecasting such as number of health-related cases expected in the days, months or years to come has tremendous planning, management, and fiscal importance. In the health sector, such analyses drive the essential policy, program development and implementation decisions. Any errors in the forecasts must be paid with the cost of lives and here is the importance of accurate forecasting.

Forecasting a time series can be broadly divided into two types. If we use only the previous values of the time series to predict its future values, it is called Univariate Time Series Forecasting. The traditional ARIMA (Auto Regressive Integrated Moving Average) modeling is a forecasting algorithm based on the idea that the information in the past values of the time series can alone be used to predict the future values. Whereas Multi Variate Time Series Forecasting, uses predictors other than the series (exogenous variables) to forecast. Deep neural networks like Long Short-Term Memory (LSTM) recurrent neural networks can almost seamlessly model problems with multiple input variables. This is a great benefit in time series forecasting, where classical linear methods can be difficult to adapt to multivariate or multiple input forecasting problems. This advanced tool can provide practical solutions to the rapidly growing universal time data with improved performance and computational efficacy [7]. We wanted to know how radon levels evolved over time from 1945 till date and how this level can be predicted for risk prevention. In this methods case study, we examined the development and application of both (S)ARIMA and LSTM model for multivariate time series forecasting with the Keras deep learning library [3,9]. Although there is application of (S)ARIMA model in health risk analysis, we could not find any prior study or experiment that applied LSTM model in the time series analysis of any public health risk, particularly the risk from exposure to indoor air radon. Therefore, our main contribution to this paper includes performance comparison between deep learning LSTM and (S)ARIMA models that validates the proposed models to be suitable for application in the area of risk analysis with minimum data pre-processing and feature sophistication.

Project Overview and Context

Radon gas is an established category one carcinogen for lung cancer [4] that releases from bedrock, enters residential buildings and can be accumulated beyond the hazardous level to human exposure (>100Bq/m3; [18]. The health hazards of radon came to the limelight over 70 years ago when a high incidence of lung cancer in Uranium miners was identified in the USA [8]. Till date, very few countries have taken regulatory actions to tackle the issue. International Residential Code of 2010 demands an active radon control system to be operational in all new buildings in radon prone areas. The Council of the European Union’s (2013) Basic Safety Standards Directive obligates the member states to control the health risk with preemptive policies. Many European and US states have implemented buildings codes incompliance to the international standards [10]. Canadian federal government adopted a model national building code (NBC) since 1941. This was revised every five to ten years with enhanced policy directions but has not imposed any legal requirements so far [11]. The NBC becomes acts only when adopted by the provincial and territorial governments [13]. Most Canadian provinces and territories revised their building codes by 2019that require builders to follow indoor radon control measures during new constructions. However, no strict regulatory obligationis in place in Canada that can require radon testing and disclosure during property transaction. Such lenient policy allows residents’ exposure to the carcinogen and consequently, there is now 31.5% higher radon level detected in the newly built houses in Canada compared to the ones built before 1992 [14].

We applied LSTM deep learning and (S)ARIMA models for time series analysis of the pilot data collected on indoor radon gas to find out the historical trends, seasonalities and forecasted level still the end of this century so that the impacting factors can be identified, and compelling evidence can be generated that stir policy to prevent radon induced lung cancer incidence. The objective of this methods case study includes exploring cutting- edge research tools for conducting a time-series analysis that can be applied in health research beyond indoor air pollution by experimenting the robustness of two methods for producing the outcomes with the highest degree of precision and lowest errors.

Research Design

Evict radon is an umbrella term attached to a range of interrelated public health research project approved by the Research Ethics Boards of the University of Calgary (REB approval 17-2239) that is applies various investigative methods to understand people’s exposure to indoor radon gas. Our study area spreads over the entire landscape of Canada and researchers across the universities from coast to coast comprising of experts from radiation biology, genomics, building science and architecture, psychology, geology, public policy, communication to public and population health (see www.evictradon.org for more details). The project leads are committed to the tri-council policy statement and ethics as well as the regional guidelines and regulations for research involving citizen science participants.

The project randomly targeted participants took informed consent and engaged with adult citizen scientists who voluntarily purchase alpha track 90+ day radon test kits that is quality controlled by the investigators. We excluded participants having lung cancer but tailored to collect a representative sample that entails all sex, gender, race, age, income groups. We continue collecting data through online survey questionnaire that is readily deidentified and collected in a format ready to analyze.

Research Practicalities

Data Collection: We collected Canadian data through Evict Radon, a consortium of researcher spread across Canada with active partnership with the citizens scientists. We used web and social media to contact study participants who purchased radon test kits and completed a survey. The test kits were sent to the lab and test results forwarded to the investigator to communicate to the participants. We gathered Swedish radon data through our partner, Radonova in Sweden.

Data Processing: AS the data came in large volume, collected over an extensive timeline, upon different numbers of observations and types of variables, we preprocessed and equalized by putting them into the same or similar scales and analyzed only the matching timeline variables to be able to compare the outcomes between the two countries. As data collection is still in progress, we picked a sample from the pilot data from both Canada and Swedish radon testing cohorts and put years of houses built in a time series from 1946 to 2020; thus, got two simulated datetime series of extend over 74 years to analyze for this case study.

Methods

Descriptive and time-series analyses we conducted using both traditional Python-Jupyter Notebook, Keras deep learning library, and time series analysis and forecasting (TSAF) toolsets in MATLAB2020b using the TSFA econometric platform. Descriptive statistics of the concentrations of indoor radon (222Rn) test results, time-series trends and seasonality analyzed, filtered to remove trends and seasonalities, thus, random fluctuations generated, and appropriate models trained to forecast and compare radon levels in houses for desired number of years in the future both for Canada and Sweden.

ARIMA/SARIMA Model

As for the timeseries prediction, historic data should be stationary where the covariance of the variable of importance is a function of lag, not of time. We found both Canadian and Swedish datasets we non-stationary through descriptive and inferential statistical Adfuller (Table 2) tests that means both datasets had trends and seasonalities (Figure 2). As per rules, we duly removed these trends and seasonalities through differential filtering and decomposition to get the stationary data with random fluctuations of radon levels suitable to assign to an ARIMA (Auto-Regressive Integrated Moving Average) model that predicted the future trends (Figure 3). Besides, we identified seasonalities in our data and that why we Deseasoned it and add an additional term to take it a step further that is then, called SARIMA [3,12]. Details of methods’ particularities with formulas and parameters are described below; the minutiae of codes and calculations are available on demand.

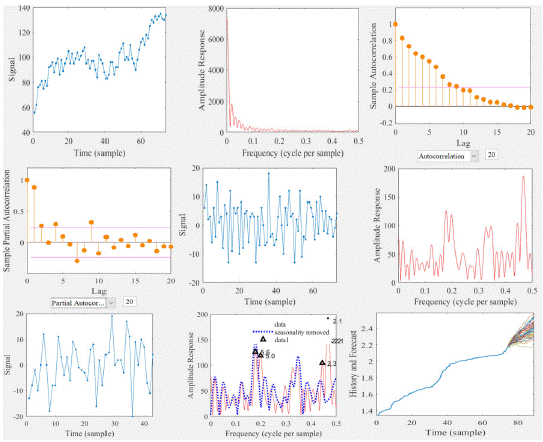
Figure 1: ARIMA/SARIMA model outputs; Canada.


    

    

    Figure 1: ARIMA/SARIMA model outputs; Canada.

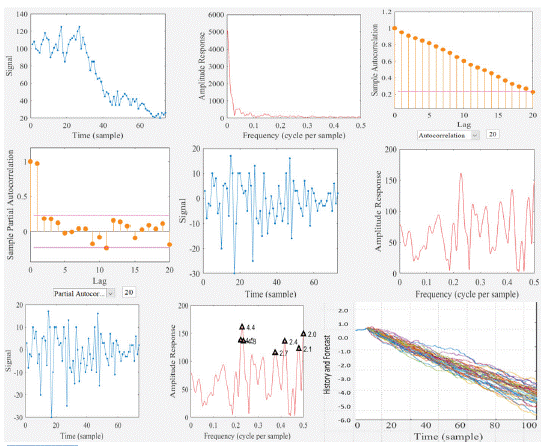
Figure 2: ARIMA/SARIMA model outputs: Sweden.


    

    

    Figure 2: ARIMA/SARIMA model outputs: Sweden.

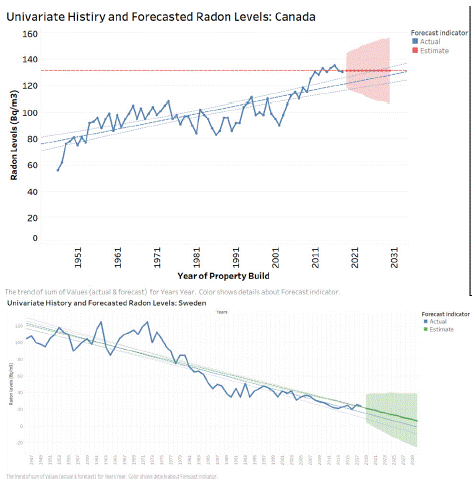
Figure 3: Deep learning LSTM Model: Canada.


    

    

    Figure 3: Deep learning LSTM Model: Canada.

Table 1: Descriptive statistics of Radon concentrations in pilot Canadian and Swedish data.








  

    Descriptive Statistics

  

  

    

    N

    Range

    Minimum

    Maximum

    Mean

    Std. Deviation

    Variance

    Skewness

    Kurtosis

  

  

    

    Statistic

    Statistic

    Statistic

    Statistic

    Statistic

    Std. Error

    Statistic

    Statistic

    Statistic

    Std. Error

    Statistic

    Std. Error

  

  

    Radon_Canada

    74

    79

    56

    135

    99.86

    1.913

    16.454

    270.749

    0.302

    0.279

    0.441

    0.552

  

  

    Radon_Sweden

    74

    105

    20

    125

    69.31

    4.016

    34.551

    1193.779

    0.71

    0.279

    -1.628

    0.552

  

  

    Valid N (listwise)

    74






Table 1: Descriptive statistics of Radon concentrations in pilot Canadian and Swedish data.

Table 2: Result of Dickey-Fuller Test.








  

    

    Canadian Data 

    Swedish Data 

  

  

    Test Statistic 

    0.335431 

    -0.961080 

  

  

    p-value 

    0.978913 

    0.767194 

  

  

    #lag Used 

    2.000000 

    6.000000 

  

  

    number of    observations used 

    74.000000 

    74.000000 

  

  

    Critical Value (1%) 

    -3.526005 

    -3.531955 

  

  

    Critical Value (5%) 

    -2.903200 

    -2.905755 

  

  

    Critical Value    (10%) 

    -2.588995 

    -2.590357






Table 2: Result of Dickey-Fuller Test.

Deep Neural Networks LSTM Model

The long short-term memory (LSTM) recurrent neural networks are a super powerful deep learning model that can seamlessly model problems with multiple input variables of time series data. It has extra benefit of in time series forecasting, where classical linear methods face difficulties in adapting to multivariate or multiple input forecasting cases. LSTM has much benefits over RNN as it can handle the memory loss and thereby prevent fading up and early disappearing of gradient descend of the neural networks. Besides, for time series forecasting, it can learn automatically from time dependent data and the can automatically handle temporal phenomena such as trends and seasonality [9].

Methods’ Particularities

Stationary in Time Series and its Types

Theatrically, a time series dataset should be stationarity to be able to forecast. Stationarity means the covariance of the variable of importance is not a function of time rather than a function of lag. The statistical time series methods and even modern machine learning methods benefit from the clearer signal in the data. We turned to the deep learning methods as the classical methods failed when the input data volume is very large and better precision is crucial. Till date, we did not know how to best model unknown nonlinear relationships in time series data and when some methods can return better performance even with non-stationary observations or when the features of stationarity and non-stationarity are coexisted. We experimented both with the traditional time series stationary data as well as data with mixed properties taking advantage of the extra analytics power of deep learning LSTM algorithms.

Examining Stationarity

We employed all the available methods to examine whether our time series data were stationary or not. These ranges from direct observations, descriptive and inferential statistical texts, residuals etc. Firstly, we reviewed the time series plots of both Canadian (left) and Swedish (right) radon data as shown below and visually checked if there we any obvious trends or seasonality.

Then, we split our time series data into three partitions, ran the summary statistics for each part and compared the mean and variance of each group. They did differ and the differences were statistically significant. As shown below the descriptive statistics of pilot sample, histograms and time series line plot logs of both Canadian and Swedish radon data showing obvious presence of deviation from normality, variances, skewness and kurtosis.

We plot the histogram of both observations to see if the data conforms to a Gaussian or normal distribution. We clearly saw the bell curve-like shape of the Gaussian distribution, with asymmetrical right-left tails. These show that indeed the distribution of radon levels did not look like a perfect Gaussian distribution, that was an indicator of non-stationary time series.

We also create a line plot of the log transformed data and can see the exponential growth seems diminished, but we still have a trend and seasonal elements. We could then calculate the mean and standard deviation of the values of the log transformed dataset.

Running the examples shows mean and standard deviation values for each group that we again similar, but not identical. Perhaps, from these numbers alone, we would say the time series is stationary, but we strongly believed this to not be the case from reviewing the line plot.

This is quick method could be misguiding; so, in the next step, we conducted inferential statistical tests to see if the expectations of stationarity were met or violated. The test was designed to explicitly comment on whether a univariate time series was stationary.

Reviewing the plot of the time series again, we could see that there was an obvious seasonality component, and it looked like the seasonality component was growing. This suggested an exponential growth from season to season. A log transform was used to flatten out exponential change back to a linear relationship. Below is the same histogram with a log transform of the time series. Running the example, we could not yet see the familiar Gaussian-like distribution of values.

Augmented Dickey-Fuller test

This test also called unit root test informs the degree to which a null hypothesis can be rejected or failed to be reject. The result determines how strongly a time series is defined by a trend. Among a number of unit root tests, Augmented Dickey- Fuller is one of the more widely used. It uses an autoregressive model and optimizes an information criterion across multiple different lag values.

The null hypothesis (H0) of the test is that the time series can be represented by a unit root, that it is not stationary (has some time-dependent structure). The alternate hypothesis (H1) rejects the null hypothesis, suggests the time series does not have a unit root, meaning it is stationary. It does not have timedependent structure. We interpret this result using the p-value from the test. A p-value below a threshold (such as 5% or 1%) suggests we reject the null hypothesis (stationary), otherwise a p-value above the threshold suggests we fail to reject the null hypothesis (non-stationary).p-value > 0.05: Fail to reject the null hypothesis (H0), the data has a unit root and is non-stationary. p-value <= 0.05: Reject the null hypothesis (H0), the data does not have a unit root and is stationary. The stats models library provides the adfuller () function that implements the test. We ran this test for both Canadian and Swedish Radon datasets.

NB: Null hypothesis in ADF test is that Data is not stationary. Here we can evaluate the test statistics for both Canadian and Swedish Data which are greater than the critical value (at 5%) and the p-value is higher than the significant value 0.05%. Thus, we failed to reject the null hypothesis and considering the data as non-stationary. Therefore, we made the data stationary by differencing and decomposing.

Thus, we determined that our radon data showed no stationary rather demonstrated different clear up and downward trends and seasonality over the shifting of time. Therefore, we modelled these components, and removed them from the observations, then trained models on the residuals. When we fitted the stationary model to our data, we assumed that our data we a realization of a stationary process.

We used the AC (autocorrelation) and PAC (partial autocorrelation) to set the preliminary idea whether our data are autoregressive or not. As a rule of thumb, if AC tails off gradually and PAC cuts of after p lags, it is an AR(p) model, whereas if AC cuts off after q lags and PAC tails off gradually, the model is MA(q); and if both AC and PAC tails off gradually then, the model should be ARMA (p. q). In both our Canadian and Swedish samples, AC and PAC tailed off gradually and that is why we integrated both AR and MA models into ARIMA model (Figure 4).

Figure 4: Deep learning LSTM Model: Sweden


    

    

    Figure 4: Deep learning LSTM Model: Sweden

Graphical Abstract


    

    

    Graphical Abstract

ARIMA Models

ARIMA is a combination of models that describes a given time series based on its own values. These values are lags and lagged forecast errors generated from the dataset through mathematical equation that forecast future values. Hence, any processed time series data that displays patterns and have no random white noise can be fitted to ARIMA model to forecast future events. An ARIMA model is described with 3 terms: p, d, q; where, p is the order of the AR term, q is the order of the MA term, and d is the number of differencing required to make the time series stationary. If a time series, has seasonal patterns, then we add an extra seasonal term and call it SARIMA that is short for Seasonal ARIMA [3,12].

Detrending

To remove trend, we used tools such as Fourier Transformation function that provides spikes in the frequency domain corresponding to the number of harmonics and we used that least common multiple of harmonics to multiply the signal that removes seasonality underlying the trends. Second, we looked for autocorrelations that intuitively signals whether the samples are related to each other or not. Where as partial autocorrelations denote almost the same thing, but they remove linear dependence on the previous samples before finding the auto correlations.

Our model had seasonalities, as the seasonal spikes were clearly visible after applying usual differencing (lag 1). so, we kept seasonal term and built a SARIMA model on for both the Canadian and Swedish using pmdarima’s auto_arima (). Thus, we set seasonal=True, set the frequency m=12 for month wise series and enforced d=1. The model has estimated the AIC (Akaike information criterion is an estimate of a constant plus the relative distance between the unknown true likelihood function of the data and the fitted likelihood function of the model, so a lower AIC of a model is considered to be closer to the truth, [17]. The P values of the coefficients also were significant. We also checked the residual diagnostics plot. The best model SARIMAX (3, 0, 0) x (0, 1, 1, 12) has an acceptable lower AIC and the P Values were significant. Then, we proceeded to forecast radon values for the desired future years.

Final Forecasts: Our model captured the expected seasonal demand patterns. Then we used that as a template (TASF) and plug-inset of variables into the code. The seasonal index acted as an exogenous variable because it repeated every frequency cycle, one year in this case. So, we would always know what values the seasonal index would hold for the future forecasts. Therefore, we have the model with the exogenous term. Considering all these, we can forecast radon levels till a desired number of years along with historical display of preferred years for both Canada and Sweden (Appendix 1: ARIMA TSAF Coding Details).

Deep Neural Networks LSTM Model

Deep learning methods opens wide scopes for time series forecasting that includes automatic learning of temporal dependence and automatic handling of temporal phenomena such as trends and seasonality. In LSTM model, we can define either a simple univariate or complex multivariate problem as a sequence of integers, fit the model on the defined sequence and train it to predict the subsequent values of the series in future. Thus, the frame the model with three-dimensional inputs as [sample, time steps, features] and reshape it using the Encoder- Decoder pattern. We processed and created time series samples of radon test results as evictradon.csv and swedishradon. csv datasets; conducted in residential properties of Canada and Sweden built since 1946 till 2020; thus, we got 74 input time steps. We defined the 6 input features as input shape argument on the first hidden layer. These are R-value, Depth_Roof_Insulation, building age, SQF-BS, SQF_GMF, number_stories - the most important predictors got from factor analysis. Then, we defined an LSTM encoder to read and encode the input sequences of 74-time steps. The encoded sequence was repeated 250 to 500 times by the model to train and produce the most accurate 10 more output time steps using repeat vector layer. These were fed to a decoder LSTM layer before using a Dense output layer wrapped in a time distributed layer that was able to produce one output for each step in the sequence. The model used the efficient Adam version of stochastic gradient descent and optimized the Mean Squared Errors (MSE) loss function. Thus, once our model was defined and training data fitted to it, the model was ready to predict. Likewise, to forecast the values of multiple time steps in the future, we used the predict and update state function to predict time steps one at a time and update the network state at each prediction [5,9]. Thus, we can sue the trained LSTM model to display history and forecasted radon levels for the next desired number of years. (Appendix 2: Deep Learning LSTM Neural Network Model coding details).

Minor details: When training networks for deep learning, it is useful to monitor the training progress by plotting various metrics during training. Thereby, we can determine whether and how rapidly the network accuracy is improving, and whether the network is starting to over fit the training data.

When we specify 'training-progress' as the 'Plots' value in training Options and start network training, train Network creates a figure and displays training metrics at every iteration. Each iteration is an estimation of the gradient and an update of the network parameters. If we specify validation data in training Options, then the figure shows validation metrics each time train Network validates the network. The figure plots the following: a) Training accuracy: Classification accuracy on each individual mini batch. B) Smoothed training accuracy: Smoothed training accuracy, obtained by applying a smoothing algorithm to the training accuracy. It is less noisy than the unsmoothed accuracy, making it easier to spot trends. c) Validation accuracy: Classification accuracy on the entire validation set (specified using training Options). d) Training loss, smoothed training loss, and validation loss: The loss on each mini batch, its smoothed version, and the loss on the validation set, respectively. If the final layer of your network is a classification Layer, then the loss function is the cross-entropy loss. For regression networks as ours, the figure plots the root mean square error (RMSE) instead of the accuracy. Our Canadian and Swedish model had the lowest RMSE of 5.92 and 6.72, respectively (Figures 3 & 4). The figure marks each training Epoch using a shaded background. An epoch is a full pass through the entire data set. We got the best training outcomes with 500 and 250 epochs for Canadian and Swedish model (Figures 3 & 4). Once training is complete, train Network returns the trained network. We can view the Results showing the final validation and the reason that training finished. The final validation metrics are labeled Final in the plots and the forecasts are shown in obvious non-linear pattern compared to linear form of (S)ARIMA model. In the figure 3 and 4 we can see the information about the training time and settings.

Analyses Outcomes

Interpretations

The overall trend of indoor radon level in Western Canada remained upwards whereas it gradually goes downwards in Sweden. Although both the predicted models have forecasted radon to be in rise in Canada and Sweden with wide margins of confidence, these scenarios can be averted by takings appropriate policy and public health measures through the objective based building codes and awareness campaigns and incentives to testing and mitigation efforts. To be noted, the theoretical zero radon level in the prediction model is not practical as radon continues to emit from the ground as well as from other building materials and the level never reaches to zero rather stays above 10 Bq/m3 at the ambient air.

Results

The pilot data the two countries have different patterns of radon (222Rn) concentrations that varied over the bicentenary. Overall, the mean annual indoor level was higher in Canada than that in Sweden. We calculated the mean and moving average radon levels for the entire dataset, identified trends and seasonality from 1946 to 2020. Thus, prepared the model to project radon levels from 2020 onwards to any reasonable number of future years. This exercise also enabled us to compare and contrast the features for Canada and Sweden. We look forward to the complete data collection and final analysis.

Conclusion

In this article, we presented the features of time series and stationary data, methods to verify whether a time series is stationary using basic summary statistics and python codes; running and interpretation of statistical significance tests to check if a time series is stationary. More specifically, we became familiar with the methods and importance of converting time series data from non-stationary to stationary for use with statistical and deep learning modeling methods. We came to know about the power of deep learning LSTM model in dealing with multiple variables when forecasting in a non-linear model that can also deal with large volume of data and overcome the limitations of ARIMA model.

Declaration of Conflict of Interest: This information will be provided after the blinded review.

References

Download PDF

Citation: Khan SM. Application of Deep Learning LSTM and ARIMA Models in Time Series Forecasting: A Methods Case Study analyzing Canadian and Swedish Indoor Air Pollution Data. Austin J Med Oncol. 2022; 9(1): 1073.

Home

Journal Scope

Editorial Board

Instruction for Authors

Submit Your Article