On The Short Delay in Neighboring Neural Pulses

Editorial

To fully reveal the physical nature of a neural signal is important for understanding the ways how neural signals are generated and transmitted. Compared with the cable model and electromechanical model, the emerging electromagnetic model attracted much attention in recent years [1-5], as it states that neural signals travel in axons are more like pulses of Electromagnetic (EM) waves travelling in EM waveguides, rather than ionic currents transporting in cables. Here we reanalyzed experimental data in published in previous literatures, calculated the average delay time at each Ranvier node in myelinated axons with electromagnetic model, and figured out a picture on the underlying relationship between the generation process and the measured propagation speed for neural signals along axons.

The propagation of neural signals in myelinated axons is measured with an average speed of 10-150 m/s [6]. Note that there are no reasonable physical processes with this similar velocity. For example, electromagnetic signals transmit at the light or near-light speed, 3×10⁸m/s, the migration of molecules in solution usually has a rate of 1nm/s driven by the electric field of 1V/m. Although the transmission of mechanical waves has similar velocity, it is obviously not the nature of neural signals. As a result, the measured propagation speed is the superficial speed, rather than the conduction speed of real neural signals.

Usually, the total delay of neural signals, behaving as action potentials, can be divided into two parts: delay on internodal segments, and delay at Ranvier nodes, i.e., ion channel group. Obviously, the delay on internodal segments could be overlooked in electromagnetic model. Because the velocity of the neural electromagnetic pulses is nearly the light speed, it needs only about 10-11 s for a neural signal to pass a single internodal segment of 1-2mm. As a result, the delay consumes mainly at Ranvier nodes, where the neural electromagnetic pulses relay (generated and amplified). According to the average internode length and measured propagation speed of neural signals at the same myelinated axons, average delay, t, at Ranvier nodes could be calculated as

τ = ^L⁄_υ

with the following formula

υ = ^ΔL⁄_ΔT  = ^N.L_in⁄_N.τ  = ^L_in⁄_τ

Where ΔL is the distance between two points under test, ΔT the total delay time between these two testing points, N the number of Ranvier nodes between two testing points, and Lin the average internode length at the myelinated axon.

Calculated with experimental data, the average delay t was found ranging from 16.3 to 87.0 μs. These values are consistent with the value of 10-50 μs obtained in direct measurement [7], and consistent with the value of 74μs (named internodal conduction time) reported by Koles et al. [8]. Surprisingly, this DELAY occupies only 0.5-5% of the duration of a single action potential, which is usually measured to be 1-2 ms in numerous experiments.

Thus the reality in propagation of action potentials is not as described in textbook: an action potential is generated by ion channel cluster at one local spot, then transmits along an axon, and triggers excitation of next ion channel cluster. Indeed, within 100μs after the first action potential is generated, the next action potential is triggered; and, the first one continuously develops into a full signal peak as measured, together with the second.

Due to these two experimental facts: the similarity of action potentials and shorter delay (‹100μs) in signal relay process, we schematically illustrate that two action potentials measured at two neighboring different nodes are overlapped highly in the same time scale, as shown in Figure 1.

    

    

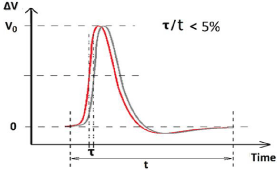
    Figure 1: The diagram for highly overlap of two neighboring action potentials.