
Research Article
Austin J Nucl Med Radiother. 2015;2(1): 1011.
Transient Acid pH Effect in Tracks in The Radiolysis of Water: Does This Effect Contribute to Biological Damage Caused by Ionizing Radiation?
Kanike V, Meesungnoen J and Jay-Gerin JP*
Department of Nuclear Medicine and Radiobiology, University of Sherbrooke, Canada
*Corresponding author: Jay-Gerin JP, Department of Nuclear Medicine and Radiobiology, Faculty of Medicine and Health Sciences, University of Sherbrooke, 3001, 12th Avenue North, Sherbrooke, QC J1H 5N4, Canada,
Received: December 16, 2014; Accepted: February 13, 2015; Published: February 16, 2015
Abstract
We present a model calculation, using Monte Carlo track chemistry simulations, which quantitatively shows that the formation of H3O+ during the primary radiolysis processes in water renders the spur/track regions more acid than the surrounding solution. Although experimental evidence for this effect has already been reported, there is only fragmentary information on its magnitude and time dependence. Here, we compare our calculated yields of H3O+ and the corresponding pH values for both low-LET (“spherical” spur model) and high-LET (“cylindrical” track model) radiation. Our calculated time evolution of G (H3O+) in the radiolysis of pure deaerated water by 300-MeV incident protons (which mimic 60Co ?/fast electron irradiation) is in very good agreement with available experimental data. For both studied cases, an abrupt transient acid pH effect is observed at times immediately after the initial energy release. This effect, which we call an “acid spike”, is found to be greatest for times shorter than ~1ns. In this time range, the pH remains nearly constant: ~3.3 in spherical spurs and ~2.5 in cylindrical tracks. Beyond ~1ns, the pH increases gradually, ultimately reaching a value of 7 at ~1 µs for the spherical spur and at a somewhat longer time (~0.1 ms) for the cylindrical track. It does not appear that the acid spike described here has been explored in water or in a cell subject to the action of ionizing radiation. In this regard, this work raises a number of questions, some of which are briefly evoked.
Keywords: Liquid water; Aqueous solution; Radiolysis; Linear energy transfer (LET); Low- and high-LET radiation; Spur; Track; Hydrogen ion; Radiation chemical yield; pH; Biological damage; Radiobiology; Radiotherapy; Hyperthermia
Introduction
Water is the major (about 70-85%) constituent of living cells. A thorough knowledge of the radiolysis of water is therefore critical for understanding radiobiological effects. The absorption of energetic radiations by water leads to the production of reactive chemical species that can damage all biomolecules, including lipids, proteins, and DNA; DNA is considered to be the most important molecule in defining the radiobiological response. Lesions randomly induced in cellular DNA by ionizing radiation can be repaired or can result in cytotoxic and mutagenic effects and chromosomal instability, all of which can contribute to tumorigenesis [1-5].
It has been customary to separate the complex succession of events that follow the irradiation of water into four, more or less clearly delineated, consecutive, temporal stages [6-9]. Briefly, the first or “physical” stage consists of the phenomena by which energy is transferred from the incident radiation to the water. Its duration is of the order of 10-16 s or less. This energy absorption gives rise, along and around the path of the radiation, to a large number of ionized (H2O•+) and electronically excited (H2O* elec) water molecules distributed in a specific, highly non-homogeneous track structure which depends on the type and energy of the radiation used. Secondary electrons generated in the ionization events have a wide range of energies. Generally, they have enough energy to ionize or excite one or more other water molecules in the vicinity. The second or “physicochemical” stage consists of the re-establishment of thermal equilibrium in the bulk medium with reactions and the reorganization of initial products to give new chemical species such as stable molecules and water free radicals. It lasts about 10-12 s. During this stage, secondary electrons slow down to thermal energy (eth ) and, following thermalization, they become trapped (etr ) and hydrated (e-aq). By ~10-12 s, the radiolysis of water can be simply described by the following reactions [8,9].
H2O H2O•+
+ e- (1)H2O H2O*elec (2)
H2O•+ + H2O ? H3O+ + •OH (3)
e- → e- th → e- tr → e- aq (4)
H2O* elec → H• + •OH (5)
where H3O+ (or equivalently, Haq +) represents the hydrated proton. In addition to the two radical species e- aq and •OH (hydroxyl radical), a small quantity of H• atoms and the molecular products H2 and H2O2 are produced. The third or “chemical” stage consists of diffusion and reactions of the reactive species leading to the re- establishment of chemical equilibrium. During this stage, the various radiolytic products present at the end of the physicochemical stage diffuse away from the site where they were originally produced and then either reacts within the tracks as they develop in time or escape into the bulk solution. At 25 °C, all intra-track reactions are essentially complete by ~10-6 s after the initial energy deposition. At this time, the species that have escaped from track reactions become homogeneously distributed throughout the bulk of the solution (also referred to as the “background”) and the radiation track no longer exists. The radical and molecular products, considered as additions to the background, are then available for reaction with dissolved solutes (if any) present (in moderate concentrations) at the time of irradiation. On a quantitative basis, the species produced in the radiolysis of pure deaerated (air-free) water at homogeneity are e- aq, H3O+, H•, •OH, OH-, H2, H2O2, O2 •- [or its protonated form HO2 •, depending on the pH; pKa (HO2 •/O2 •-) = 4.8 in water at 25 °C], etc. In air-saturated solutions (the concentration of oxygen is ~0.25 mM), e- aq and H• atoms are rapidly (on a time scale of a few tenths of a microsecond) converted to superoxide anion/hydroperoxyl radicals. Thus, in an aerobic cellular environment at pH 7, the major reactive species at homogeneity include O2 •-, •OH, and H2O2 (H2 plays only a limited role in the radiolysis of aqueous solutions, and most of it escapes from solution). Finally, in a physiological system, there follows a “biological” stage in which the cells respond to the damage resulting from the products formed in the preceding stages (~10-3 s or longer, depending very much upon the medium). A good summary of the present status of aqueous radiation chemistry is given in [9-13].
Many experimental and theoretical studies have shown that the yields in the radiolysis of water are strong functions of the quality of the incident radiation, a measure of which is given by the “Linear Energy Transfer” (LET) (also called “stopping power” by physicists) that represents the non homogeneity of the energy deposition on a sub-microscopic scale, commonly referred to as the “track structure” [8,9,14]. (Throughout this article, radiation chemical yields are given as G-values, in units of radicals, ions or molecules per 100 eV of energy deposited; for conversion into SI units, 1 molecule/100 eV ≈ 0.10364 μmol/J.) At the lowest LET (e.g., for sparsely ionizing radiation such as γ-rays from 60Co, fast electrons or ~300 MeV protons generated by a particle accelerator, LET ~ 0.3 keV/μm), tracks are formed initially by well-separated Magee-type “spurs” [15,16] (spherical in shape) that develop independently in time (without interference from the neighbouring spurs). In this case, the predominant effect is radical production. As LET increases, the mean separation distance between the spurs decreases and the isolated spur structure changes to a situation in which the spurs overlap and form a dense continuous column (cylinder shape). This permits more radicals to be formed in close proximity with correspondingly greater probability of reacting with one another to produce molecular products or to reform water. High-LET, densely ionizing radiation therefore tends to produce high yields of molecular products, at the expense of free-radical yields [9,17]. To illustrate this point, {Figure 1} shows typical twodimensional representations of the track segments of 300- and 0.15- MeV irradiating protons (LET ~ 0.3 and 70 keV/μm, respectively) on liquid water at 25 °C, calculated with our IONLYS Monte Carlo simulation code {Figure 1}.
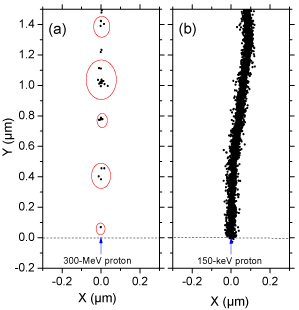
Figure 1: Projections over the XY plane of track segments of 300 (a) and
0.15 (b) MeV protons (LET ~ 0.3 and 70 keV/μm, respectively) incident on
liquid water at 25 °C, calculated (at ~10-13 s) with our IONLYS Monte Carlo
track-structure simulation code (see text). The two irradiating protons are
generated at the origin and start traveling along the Y axis. Dots represent
the energy deposited at points where an interaction occurred. Note that the
penetration range of 1H+ in liquid water, at the considered energy of 0.15 MeV,
amounts to ~2.3 μm [18].
Herein, we present a model calculation, using Monte Carlo track chemistry simulations, which quantitatively shows that the formation of H3O+ in reaction (3) during the primary radiolytic processes in water renders the spur/track regions temporarily more acid than the body of the solution. Although experimental evidence for this transient acid pH effect has already been reported [10,19,20], there is only fragmentary information on its magnitude and time dependence following energy deposition. Moreover, the influence of the quality (or LET) of the radiation on G (H3O+) has not been investigated. In this work, we compare the calculated yields of H3O+ and the corresponding pH values for both low-LET (“spherical” spur model) and high-LET (“cylindrical” track model) radiation.
Monte Carlo Track Chemistry Simulations of Water Radiolysis
Monte Carlo simulations of the complex succession of events that are generated in pure, deaerated liquid water following the absorption of ionizing radiation were performed using our IONLYS-IRT code. This program simulates, in a three-dimensional geometrical environment, the non homogeneous distribution of reactive species initially produced by the absorption of the incident radiation and all of the energetic secondary electrons, as well as the subsequent chemical reactions of these species. A detailed description of the code has been reported previously [9,17,21-23]. Briefly, the IONLYS program is used to model the early physical and physicochemical stages of radiation action up to ~10-12 s in the track development. It actually models, event by event, all the basic physical interactions (energy deposition) and the radical and molecular products of the radiolysis, distributed in a highly non homogeneous track structure. The complex spatial distribution of reactants at the end of the physicochemical stage, which is provided as an output of the IONLYS program, is then used directly as the starting point for the subsequent non homogeneous/homogeneous chemical stage. Our IRT program models this stage during which the different species diffuse randomly at rates determined by their diffusion coefficients and react with one another, or competitively with any dissolved solutes present at the time of irradiation. This program employs the “Independent Reaction Times” (IRT) method [22,24,25], a computer-efficient stochastic simulation technique that is used to simulate reaction times without having to follow the trajectories of the diffusing species. The IRT method relies on the approximation that the reaction time of each pair of reactants is independent of the presence of other reactants in the system. Its implementation has been described in detail [22], and its ability to give accurate time-dependent chemical yields under different irradiation conditions has been well validated by comparison with full random flights (or “step-by-step”) Monte Carlo simulations, which do follow the reactant trajectories in detail [26,27].
The reaction scheme for the radiolysis of pure, deaerated liquid water at 25 °C used in IONLYS-IRT is the same as used previously [28]. Values for the diffusion coefficients of the reactive species involved in the simulations are listed in Table 6 of [17].
To reproduce the effects of low-LET radiation, which predominantly produces spherical spurs separated by large distances, we used short segments of 300MeV incident proton tracks (Figure 1), over which the average LET value obtained in the simulations was nearly constant and equal to ~0.3 keV/μm at 25 °C. (Such model calculations thus gave “track segment” yields at a well-defined LET [14]. The influence of the LET of the radiation on the yields of G(H3O+) was investigated by performing a series of simulations with protons of different initial energies and therefore different LET. In this study, we limited ourselves to the incident proton energy of 0.15 MeV, corresponding to a LET value of ~70 keV/μm [29]. In this case, spurs are formed so close to each other along the path of the irradiating proton that they merge to form a cylindrical region of high LET (Figure 1). In either case, at low dose rates (so that no track overlap occurs), each spherical spur or cylindrical track can be treated independently from all others.
The simulations consist of following the transport and energy loss of an incident proton until it has penetrated the chosen length (~20-150 μm) of the track segment into the medium. Due to its large mass, the impacting proton is almost not deflected by collisions with the target electrons. Typically, about 5000 to 35000 reactive chemical species are generated in the chemical development of such simulated track segments (depending on the LET). The number of proton histories (usually ~30-150, depending on the proton energy) was chosen to permit averaging of chemical yields with acceptable statistical confidence.
In the simulations reported here, the time evolution of G (H3O+) has been followed until ~1 ms.
Results and Discussion
Figure 2 shows the time evolution of G (H3O+) as obtained from our simulations of the radiolysis of pure deaerated liquid water by 300- and 0.15-MeV incident protons (LET ~ 0.3 and 70 keV/μm, respectively) at ambient temperature. For the sake of comparison, available experimental data for 60Co γ/fast electron irradiation [30- 34] are also included in the figure. As can be seen, our simulated values agree very well with the measured H3O+ yields. The sharp decrease of G (H3O+) observed at times longer than ~10 μs for 300- MeV irradiating protons is mainly due to H3O+ reacting with OH- and, to a lesser extent, with the hydrated electrons escaping the spurs, according to:
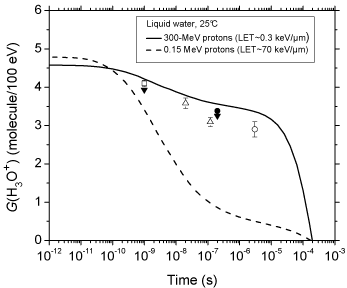
Figure 2: Time evolution of the yield (in molecule/100 eV) of hydrogen ions
for the radiolysis of pure, deaerated liquid water by 300- and 0.15-MeV
incident protons (LET ~ 0.3 and 70 keV/μm, respectively) at 25 °C from ~1
ps to 1 ms. The solid and dashed lines show the corresponding values of
G(H3O+) obtained from our Monte Carlo simulations (see text). Experimental
data for 60Co γ/fast electron (~0.3 keV/μm) irradiation: (□) [30], (▼) [31], (?)
[32], (●) [33], and (○) [34]. There are no experimental data available for 0.15-
MeV irradiating protons with which to compare our results.
H3O+ + OH- → 2H2O k6 = 1.18 × 1011 M-1 s-1 (6)
H3O+ + e- aq → H• + H2O k7 = 2.13 × 1010 M-1 s-1 (7)
where k6 and k7 are the rate constants for the two individual reactions [13,28]. The time dependence of the cumulative yield variations ΔG (H3O+) for the different reactions that contribute to G (H3O+) (data not shown here) confirms that the decrease of G (H3O+) at long times is predominantly due to reaction (6) in the stage of homogeneous chemistry. To our knowledge, there are no experimental data of G (H3O+) available for 0.15-MeV irradiating protons with which to compare our results. In this case, our simulations show that the decay of H3O+ with time still largely results from reactions (6) and (7), although there is also a relatively small contribution due to the following reactions [13,28].
H3O+ + O•- → •OH + H2O k8 = 5 × 1010 M-1 s-1 (8)
H3O+ + HO2 - → H2O2 + H2O k9 = 5 × 1010 M-1 s-1 (9)
however, as shown in Figure. 2, the decrease in G (H3O+) occurs as early as ~102 picoseconds up to microseconds, which is clearly different from what is observed for irradiation with 300-MeV incident protons (which mimic 60Co γ/fast electron irradiation). As expected, this is consistent with differences in the initial spatial distribution of primary transient species (i.e., in the track structure). As mentioned earlier, in the track (columnar) geometry of the higher-LET 0.15- MeV irradiating protons, the reactive intermediates are formed locally in much closer initial proximity than in the spur (spherical) geometry, which favours the incidence, at shorter time scales, of an increased amount of intervening intra-track reactions.
With the objective of calculating the pH values prevailing in the spur/track regions, we now need to estimate the concentrations of H3O+ generated in situ in these regions as a function of time. Two models are considered depending on the quality (LET) of the radiation.
For 300-MeV incident protons (LET ~ 0.3 keV/μm), we assume that the hydronium ions are produced evenly in an isolated spherical spur whose initial radius ro (prior to spur expansion) is equal to the average electron thermalization distance obtained from our simulations (ro = 11.7 nm) [23]. The low-LET spur concentrations of H3O+ are derived from
where the mean energy loss in a single event (i.e., the mean energy deposited in a spur) is taken to be ~47 eV [21,28,35] and
r(t)2 = ro 2 + 6 D t (11)
represents the change with time of ro due to the (three dimensional) diffusive expansion of the spur. Here, t is time and D is the diffusion coefficient of H3O+ in water (D = 9.46 × 10-9 m2 s-1 at 25 °C) [17,22].
For 0.15-MeV irradiating protons (LET ~ 70 keV/μm), we consider the track as being a cylinder, homogeneous along its axis, of length L = 1 μm and initial radius rc equal to the radius of the physical track “core” (which corresponds to the tiny radial region within the first few nanometers around the impacting ion path, at ~10-13 s) [8,36]. In this case, the high-LET track concentrations of H3O+ can be obtained from [9].
Where
r(t)2 = ro 2 + 4 D t (13)
represents the change with time of rc due to the (two dimensional) diffusive expansion of the track. Here, rc was obtained from our simulations [29] and is taken to be ~25 nm.
Using Eqs. (10) and (12) readily gives the concentrations of H3O+ as a function of time for both isolated “spherical” spurs and axially homogeneous “cylindrical” tracks. The pH in the corresponding spur/track regions is then simply given by the negative logarithm of [H3O+]:
The time evolution of the pH values calculated as indicated above for 300- and 0.15-MeV incident protons in pure, deaerated liquid water (LET ~ 0.3 and 70 keV/μm, respectively) using the spherical spur and cylindrical track models at 25 °C is shown in Figure. 3. As can be seen, for both radiations considered, there is an abrupt transient acid pH effect at times immediately after the initial energy release. This effect, which we call an “acid spike” in analogy with the “thermal spike” used in radiation chemistry to describe the formation of a transient excess temperature region around the tracks of high-LET accelerated heavy ions [14,37], is found to be greatest for times shorter than ~1 ns. In this time range, the pH remains nearly constant, equal to ~3.3 in spherical spurs and ~2.5 in cylindrical tracks. Beyond ~1 ns, the pH increases gradually for the two cases studied, ultimately reaching a value of 7 (neutral pH) at ~1 μs for the spherical spur geometry (corresponding to the end of spur expansion and the beginning of homogeneous chemistry [9-12]) and at a somewhat longer time (~0.1 ms) for the cylindrical track geometry.
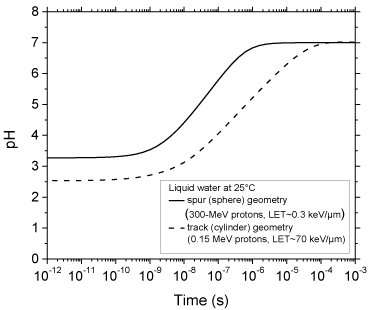
Figure 3: Variation of pH with time calculated for 300-MeV incident protons
(LET ~ 0.3 keV/μm) using the isolated “spherical” spur model (solid line),
characteristic of low-LET radiation, and for 0.15-MeV incident protons (LET ~
70 keV/μm) using the axially homogeneous “cylindrical” track model (dashed
line), characteristic of high-LET radiation, at 25 °C from ~1 ps to 1 ms (see
text).
To the best of our knowledge, the acid spike effect described above has not been explored in water or in a cell subject to the action of ionizing radiation, especially high-LET radiations (e.g., a-particles, high charge and high energy particles). In this respect, this work raises a number of questions. For example, in radiation chemistry, does the generation of strongly acidic regions, which extend over spatial dimensions of the order of tens of nanometres, have any noticeable influence on the final product formation by affecting all pH-dependent species and reaction rates [37,38]? In radiation- and free radical-biology, as many cellular processes depend on pH [39,40], is this transient acid pH, which is well outside the physiological range, toxic to cells (e.g., by attacking DNA, by causing oxidative injury, by modifying normal biochemical reactions, or by triggering different signalling cascades that respond to these stress conditions [5]), and could it contribute to the initial events that lead to cell damage, enhanced lethality, “bystander” responses (where stressful effects are propagated from irradiated cells to non-targeted neighbours) [41- 43], or genomic instability in progeny of irradiated cells and their neighbouring bystanders [44,45]? In the development of effective therapies for malignant diseases, do these spikes of acidity have any adverse effect on the response of cells to conventional anticancer drugs and possibly influence the outcome of tumor therapy [39]? Finally, it has been demonstrated that cells in an acid pH environment are more sensitive to the lethal effect of heat [46]. Thus, this work also raises the question of whether the highly acidic environment generated in the spurs/tracks of the radiation could explain, at least partly, why the combination of hyperthermia and radiotherapy is synergistic (in other words, why hyperthermia is a very effective radio sensitizer) and works best when the two are applied simultaneously [39,47-49].
Conclusion
In this work, Monte Carlo track chemistry simulations have been used in an attempt to quantify the “acid spike” effect that is generated in situ in tracks in the radiolysis of water during the primary radiolytic processes. Two track models were considered depending on the quality (LET) of the radiation: an isolated “spherical” spur model (associated with 300-MeV irradiating protons, LET ~ 0.3 keV/μm) and an axially homogeneous “cylindrical” track model (corresponding to 0.15-MeV incident protons, LET ~ 70 keV/μm). For times shorter than ~1 ns, the pH was found to be nearly constant in both cases: equal to ~3.3 in isolated spurs and ~2.5 in cylindrical tracks. Beyond ~1 ns, the pH increased gradually for both studied cases, ultimately reaching a value of 7 (neutral pH) at ~1 μs (corresponding to the lifetime of the spur) for the spherical geometry and ~0.1 ms for the cylindrical geometry
We should also emphasize here the very good agreement of our calculated time evolution of G(H3O+) in the radiolysis of pure deaerated water by 300-MeV incident protons (which mimic 60Co γ/ fast electron irradiation) with available experimental data at 25 °C.
It does not appear that the transient acid pH effect that we have described has been explored in water or in a cell subject to the action of ionizing radiation, especially high-LET radiation. In this regard, this work raises a number of questions, some of which have been briefly evoked.
Acknowledgment
We thank Professor Edouard I. Azzam of New Jersey Medical School Cancer Center for his valuable comments. The financial assistance of the Natural Sciences and Engineering Research Council of Canada (Grant No. 9020-2010) is gratefully acknowledged.
References
- Von Sonntag C. Free-Radical-Induced DNA Damage and its Repair. A Chemical Perspective. Berlin: Springer-Verlag. 2006.
- Becker D, Sevilla MD. The chemical consequences of radiation damage to DNA. Adv Radiat Biol. 1993; 17: 121-180.
- Cadet J, Berger M, Douki T, Ravanat JL. Oxidative damage to DNA: formation, measurement, and biological significance. Rev Physiol Biochem Pharmacol. 1997; 131: 1-87.
- O’Neill P. Radiation-induced damage in DNA. Jonah CD, Rao BSM, editors. In: Radiation Chemistry: Present Status and Future Trends. Amsterdam: Elsevier. 2001; 585-622.
- Azzam EI, Jay-Gerin JP, Pain D. Ionizing radiation-induced metabolic oxidative stress and prolonged cell injury. Cancer Lett. 2012; 327: 48-60.
- Platzman RL. The physical and chemical basis of mechanisms in radiation biology. Claus WD, editor. In: Radiation Biology and Medicine. Selected Reviews in the Life Sciences. Reading: Addison-Wesley. 1958; 15-72.
- Kuppermann A. Theoretical foundations of radiation chemistry. J Chem Ed. 1959; 36: 279-285.
- Chatterjee A, Holley WR. Computer simulation of initial events in the biochemical mechanisms of DNA damage. Adv Radiat Biol. 1993; 17: 181-226.
- Meesungnoen J, Jay-Gerin JP. Radiation chemistry of liquid water with heavy ions: Monte Carlo simulation studies. Hatano Y, Katsumura Y, Mozumder A, editors. In: Charged Particle and Photon Interactions with Matter: Recent Advances, Applications, and Interfaces. Boca Raton: Taylor & Francis. 2010; 355-400.
- Spinks JWT, Woods RJ. An Introduction to Radiation Chemistry. 3rd edn. New York: Wiley. 1990.
- Ferradini C, Jay-Gerin JP. La radiolyse de l’eau et des solutions aqueuses: historique et actualite. Can J Chem. 1999; 77: 1542-1575.
- Buxton GV. Radiation chemistry of the liquid state: (1) Water and homogeneous aqueous solutions. Farhataziz, Rodgers MA, editors. In: Radiation Chemistry: Principles and Applications. New York: VCH Publishers. 1987; 321-349.
- Elliot AJ, Bartels DM. The reaction set, rate constants and g-values for the simulation of the radiolysis of light water over the range 20 to 350°C based on information available in 2008. Report AECL-153-127160-450-001. Atomic Energy of Canada Limited, Chalk River, Ontario, Canada. 2009.
- LaVerne JA. Track effects of heavy ions in liquid water. Radiat Res. 2000; 153: 487-496.
- Magee JL. Radiation chemistry. Annu Rev Nucl Sci. 1953; 3: 171-192.
- Mozumder A, Magee JL. Model of tracks of ionizing radiations for radical reaction mechanisms. Radiat Res. 1966; 28: 203-214.
- Sanguanmith S, Muroya Y, Tippayamontri T, Meesungnoen J, Lin M, Katsumura Y, et al. Temperature dependence of the Fricke dosimeter and spur expansion time in the low-LET high-temperature radiolysis of water up to 350 °C: a Monte-Carlo simulation study. Phys Chem Chem Phys. 2011; 13: 10690-10698.
- Watt DE. Quantities for Dosimetry of Ionizing Radiations in Liquid Water. London: Taylor & Francis. 1996.
- Smith DR, Stevens WH. Radiation-induced hydrolysis of acetal: Evidence for the reaction of H3O+ ions in spurs in the radiolysis of water. Nature. 1963; 200: 66-67.
- Anbar M, Thomas JK. Pulse radiolysis studies of aqueous sodium chloride solutions. J Phys Chem. 1964; 68: 3829-3835.
- Cobut V, Frongillo Y, Patau JP, Goulet T, Fraser MJ, Jay-Gerin JP. Monte Carlo simulation of fast electron and proton tracks in liquid water. I. Physical and physicochemical aspects. Radiat Phys Chem. 1998; 51: 229-243.
- Frongillo Y, Goulet T, Fraser MJ, Cobut V, Patau JP, Jay-Gerin JP. Monte Carlo simulation of fast electron and proton tracks in liquid water. II. Nonhomogeneous chemistry. Radiat Phys Chem. 1998; 51: 245-254.
- Meesungnoen J, Jay-Gerin JP. High-LET radiolysis of liquid water with 1H+, 4He2+, 12C6+, and 20Ne9+ ions: effects of multiple ionization. J Phys Chem A. 2005; 109: 6406-6419.
- Tachiya M. Theory of diffusion-controlled reactions: Formulation of the bulk reaction rate in terms of the pair probability. Radiat Phys Chem. 1983; 21: 167-175.
- Pimblott SM, Pilling MJ, Green NJB. Stochastic models of spur kinetics in water. Radiat Phys Chem. 1991; 37: 377-388.
- Goulet T, Fraser MJ, Frongillo Y, Jay-Gerin JP. On the validity of the independent reaction times approximation for the description of the nonhomogeneous kinetics of liquid water radiolysis. Radiat Phys Chem. 1998; 51: 85-91.
- Plante I. Développement de codes de simulation Monte-Carlo de la radiolyse de l’eau et de solutions aqueuses par des electrons, ions lourds, photons et neutrons. Applications a divers sujets d’interet experimental. PhD Thesis. Universite de Sherbrooke, Sherbrooke, Quebec, Canada. 2008.
- Mirsaleh Kohan L, Sanguanmith S, Meesungnoen J, Causey P, Stuart CR, Jay-Gerin JP. Self-radiolysis of tritiated water. 1. A comparison of the effects of 60Co ?-rays and tritium ?-particles on water and aqueous solutions at room temperature. RSC Adv. 2013; 3: 19282-19299.
- Muroya Y, Plante I, Azzam EI, Meesungnoen J, Katsumura Y, Jay-Gerin JP. High-LET ion radiolysis of water: visualization of the formation and evolution of ion tracks and relevance to the radiation-induced bystander effect. Radiat Res. 2006; 165: 485-491.
- Pikaev AK, Kabakchi SA, Zansokhova AA. Yields and reactions of hydrogen ions on radiolysis of water and aqueous solutions. Faraday Disc. Chem Soc. 1977; 63: 112-123.
- Cercek B, Kongshaug M. Hydrogen ion yields in the radiolysis of neutral aqueous solutions. J Phys Chem. 1969; 73: 2056-2058.
- Anderson RF, Vojnovic B, Michael BD. The radiation-chemical yields of H3O+ and OH? as determined by nanosecond conductimetric measurements. Radiat Phys Chem. 1985; 26: 301-303.
- Barker GC, Fowles P, Sammon DC, Stringer B. Pulse radiolytic induced transient electrical conductance in liquid solutions. 1. Technique and the radiolysis of water. Trans Faraday Soc. 1970; 66: 1498-1508.
- Schmidt KH, Ander SM. Formation and recombination of H3O+ and hydroxide in irradiated water. J Phys Chem. 1969; 73: 2846-2852.
- Autsavapromporn N. The effects of pH and radiation quality (LET) on the radiolysis of liquid water and aqueous solutions: A study by using Monte Carlo simulations. MSc Thesis. Burapha University, Bangsaen, Chonburi, Thailand. 2006.
- Magee JL, Chatterjee A. Track reactions of radiation chemistry. Freeman GR, editor. In: Kinetics of Nonhomogeneous Processes. New York: Wiley. 1987; 171-214.
- Draganic IG, Draganic ZD. The Radiation Chemistry of Water. New York: Academic Press. 1971.
- Ferradini C, Jay-Gerin JP. The effect of pH on water radiolysis: A still open question– A minireview. Res Chem Intermed. 2000; 26: 549-565.
- Tannock IF, Rotin D. Acid pH in tumors and its potential for therapeutic exploitation. Cancer Res. 1989; 49: 4373-4384.
- Errera M, Forssberg A. Mechanisms in Radiobiology: Multicellular Organisms. Burlington: Elsevier. 2013.
- Nagasawa H, Little JB. Induction of sister chromatid exchanges by extremely low doses of a-particles. Cancer Res. 1992; 52: 6394-6396.
- Buonanno M, de Toledo SM, Pain D, Azzam EI. Long-term consequences of radiation-induced bystander effects depend on radiation quality and dose and correlate with oxidative stress. Radiat Res. 2011; 175: 405-415.
- Ponnaiya B, Suzuki M, Tsuruoka C, Uchihori Y, Wei Y, Hei TK. Detection of chromosomal instability in bystander cells after Si490-ion irradiation. Radiat Res. 2011; 176: 280-290.
- Azzam EI, Little JB. The radiation-induced bystander effect: evidence and significance. Hum Exp Toxicol. 2004; 23: 61-65.
- Morgan WF. Non-targeted and delayed effects of exposure to ionizing radiation: II. Radiation-induced genomic instability and bystander effects in vivo, clastogenic factors and transgenerational effects. Radiat Res. 2003; 159: 581-596.
- Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. 6th edn. Philadelphia: Lippincott Williams & Wilkins. 2006.
- Horsman MR, Overgaard J. Hyperthermia: a potent enhancer of radiotherapy. Clin Oncol (R Coll Radiol). 2007; 19: 418-426.
- Kampinga HH. Cell biological effects of hyperthermia alone or combined with radiation or drugs: a short introduction to newcomers in the field. Int J Hyperthermia. 2006; 22: 191-196.
- Hainfeld JF, Lin L, Slatkin DN, Avraham Dilmanian F, Vadas TM, Smilowitz HM. Gold nanoparticle hyperthermia reduces radiotherapy dose. Nanomedicine. 2014; 10: 1609-1617.