
Review Article
Austin J Pharmacol Ther. 2024; 12(3): 1192.
Dose Adjustments in Renal Failure: Does the Dettli Formula Need an Update Moving Away from Linearity?
Wolfgang Scholz*
SCHOLZ Data Bank, Founder, Department for Medical-Pharmaceutical Information, USA
*Corresponding author: Wolfgang Scholz, SCHOLZ Data Bank, Founder, Department for Medical-Pharmaceutical Information, 1270 Avenue of the Americas, NY 10020, USA. Email: wscholz@scholzdatabank.com; www. scholzdatabank.com
Received: September 28,2024; Accepted: October 18, 2024 Published: October 25, 2024
Introduction
Chronical Kidney Disease (CKD) causes deterioration of renal function with reduction of glomerular filtration (GFR). Drugs which are mainly excreted through the kidney have reduced renal elimination (Clrenal) in CKD. For decades dosage adjustments for these drugs have been computed based on GFR and clearance measurement of biomarker serum creatinine (Clcr), respectively, and according to the rule of Dettli [1-3] where the appropriate dose D compared to the normal dose (Dnorm) may be assessed through the individual elimination fraction Q:
Equation 1) Q = Qo + (1 – Qo) * GFR ml/min / 100 ml/min;
Qo = extrarenal elimination fraction
Equation 2) D = Dnorm * Q
Problem
Renal clearance based on GFR is not the only mechanism which has an impact on renal drug elimination. There is also tubular secretion. The intact nephron hypothesis” claims that any stage of CKD has quantitatively the same consequences for Clcr or GFR and tubular secretion (Cls). However, that has been questioned as filtration takes place at a different site in the renal system than Cls. GFR and Cls may not go parallel in CKD [5].
The quotient of Clrenal and GFR indicates, if they go parallel or not; it is called RnF [5] (renal to filtration clearance with fraction unbound (fu) neglectable at this time in this context as this constant fu is 1 or close to 1 in most cases).
Equation 3) RnF = Clrenal / fu * GF
There are three possibilities
a) RnF increases across the range of decreasing GFR
b) RnF decreases across the range of decreasing GFR
c) RnF remains stable across the range of GFR
Chapron et al. [5] evaluated data for 27 drugs and found that RnF showed significant changes of RnF for 13 drugs across the range of falling GFR with RnF decreasing in 10 and increasing in 3 cases.
Regression analysis revealed the following type of equation:
Equation 4) RnF = a + b * GFR
There are three cases for b:
Case a) b < 0: GFR falls more rapidly than Cls
Consequently, Clrenal measured through GFR is too low compared with Clrenal measured based on RnF and GFR. GFR alone therefore underpredicts Clrenal and dose adjustments might lead to subtherapeutic drug plasma levels.
Case b) b > 0: Cls falls more rapidly than GFR
Consequently, Clrenal measured through GFR is too high compared with Clrenal measured based on RnF and GFR. GFR alone therefore overpredicts Clrenal, according to Chapron et al on average by 22-48% in patients with CKD 3B (5). The error on relying on GFR measuring Clrenal of the drug is more pronounced the worse is CKD and the lower is GFR. Dose adjustments based on Q as function solely of GFR might lead to high drug plasma levels with the risk of overdosing.
Case c) b = 0: GFR and Cls go parallel
-> Clrenal = a * GFR; Clrenal remains subject to linear functions.
Shifting the way of computing Clrenal from First Order to Second Order functions
Chapron et al. do not point out explicitly which type of function might substitute the linear relationship between Clrenal of a drug and GFR.
For Clrenal, however, may be concluded equation 5) based on compiling equations 3) and 4):
Equation 5) Clrenal = RnF * GFR = (a + b * GFR) * GFR = a * GFR + b * GFR²
The computation of Q according to equation 1) is then modified as follows:
Equation 6) Q = Qo + (1 – Qo) * Clrenal / RnF * 100
Substituting Clrenal, RnF and setting GFR = 100 as normal value in the denominator:
Equation 7a) Q = Qo + (1 – Qo) * (a + b * GFR) * GFR / (a + b * 100) * 100
Equation 7b) Q = Qo + (1 – Qo) * (a + b * GFR) * GFR / (a * 100 + b* 100 * 100) or finally
Equation 8) Q = Qo + (1 – Qo) * (a * GFR + b * GFR²) / (a * 100 + b * 100²)
Equations 5) and 8) are not any more of first order (linear) but due to the tubular contribution to Clrenal and Q respectively of second order with a graph which may show dependent on b either a concave or convex shape compared to the linear Dettli graph.
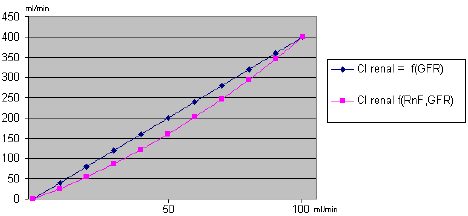
Graph 1: Metformin clearance dependent on GFR or RnF and GFR.
Theory
For the 10 drugs where RnF decreases with decreasing GFR (b > 0) and the 3 drugs where RNF increases with decreasing GFR (b < 0) the relationship between parameters GFR and RnF is linear in all cases and presents rather consistent in this respect. Therefore, a common underlying mechanism in both groups may be assumed.
Chapron et al. discuss three considerations one of which is very compelling for explaining the discordance of GFR and Cls and Clrenal respectively in the "b > 0 group". Renal plasma flow distributes 20% to filtration and the remaining 80% to the flow through the capillaries surrounding the tubules. Therefore, they conclude that with decreasing GFR the concentration of uremic solutes in the capillary blood flow increases. These uremic solutes may compete with drugs at the tubular transporter systems (e.g. OAT, OCT, MATE2) if their tubular concentrations are elevated. In consequence the secretion of these drugs might be diminished. That would mean that GFR has both a direct and additionally an indirect impact by affecting the tubular secretion on the total Clrenal of drugs the elimination of which is subject to filtration as well as to tubular secretion. Furthermore, equation 5) becomes substantially more reasonable and gains substantially more sense when backed up by such theory. More research is needed to elucidate how tubular secretion and its kinetics may develop in CKD and if from such kinetic changes a link to equation 4) may be deducted.
Clinical Consequences
Based on the evaluation of Chapron et al. [5] there is evidence that the hypothesis of the “intact nephron” as well as the theory of the linear Dettli formula to compute dose adjustments of drugs in CKD are frequently not valid and applicable. Through their evaluations these authors delivered the basis to question these theories and the linear relationship between Clrenal of drugs and GFR and consequently emphasize that effective dosing of secreted drugs in patients with CKD requires to include the aspect of renal tubular secretion.
Chapron et al. do not point out explicitly which type of function might substitute the linear relationship between Clrenal of a drug and GFR. The undersigner concludes from their data that moving away from linearity to a second order function may help to describe the relationship between Q, Clrenal and GFR in a more appropriate and more correct manner than using the linear function of Dettli for drugs where the parameters needed beyond GFR are known. Thereby a personalized medicine may be improved and the prevention of overdosing and consecutive adverse effects may be supported, for example in the case of metformin or other drugs depending predominantly on renal elimination with tubular secretion and having a narrow therapeutic index. The clearance of metformin is assumed to be 400 ml/min and more in healthy subjects [4]. Applying Equation 8 with a = 2,4 and b = 0,016, estimated values in rough accordance with RnF values presented by Chapron et al. [5], demonstrates that with falling GFR especially in the range from 70 to 10 ml/min the metformin clearance computed according to Dettli might be too high some 10 up to 40% as shown in Graph 1.
Surveys in literature indicate that metformin is commonly prescribed for patients with estimated GFR down to 30 ml/min [4] and usage for patients below that 30ml/min value is contraindicated according to most recent prescriber information [6]. If however, the “real” metformin clearance computed by equation 5) is 86 ml/min instead of 120 ml/min based on the traditional GFR based calculation and a GFR of 30 ml/min, causing a substantial risk of overdosing and lactatacidosis, there is good reason for more clinical research to further explore if the Dettli formula needs an update as proposed.
References
- Dettli L, Spring P, Habersang R. Drug dosage in patients with impaired renal function. Postgrad Med J Suppl. 1970: 32-35.
- Dettli LC. Drug Dosage in patients with renal disease. Clin Pharmacol Ther. 1974; 16: 274-280.
- Dettli L. Drug Dosage in renal disease. Clin Pharmacokinet. 1976; 1: 126- 134.
- Graham GG, Punt J, Arora M, Day RO, Doogue MP, Duong JK, et al. Clinical pharmacokinetics of metformin. Clin Pharmacokinet. 2011; 50: 81-98.
- Chapron A, Shen DD, Kestenbaum BR, Robinson-Cohen C, Himmelfarb J, Yeung CK. Does Secretory Clearance Follow Glomerular Filtration Rate in Chronic Kidney Diseases? Reconsidering the Intact Nephron Hypothesis. Clin Transl Sci. 2017; 10: 395-403.
- Prescriber Information Metformin HCL 1000 mg Bryant Ranch revised. 2024.