Femoral Torsion in CT: Why We Should Add Some Trigonometry

Research Article

Austin J Radiol. 2021; 8(1): 1120.

Femoral Torsion in CT: Why We Should Add Some Trigonometry

Konig F, Rutz E, Jacobson JA, Falkowski AL and Magerkurth O*

- Department of Radiology, Kantonsspital Baden, Im Ergel, Baden Switzerland 5404

- Hugh Williamson Gait Laboratory, Pediatric Orthopedic Department, The Royal Children’s Hospital, Parkville, Melbourne, VIC 3052, Australia

- Murdoch Children’s Research Institute, Melbourne, VIC 3052, Australia

- Department of Pediatrics, The University of Melbourne, Melbourne, VIC 3052, Australia

- Medical Faculty, The University of Basel, 4001 Basel, Switzerland

- Department of Radiology, Orthopedic University Hospital Balgrist, University of Zurich, Forchstrasse 340, 8008 Zurich, Switzerland

- Department of Radiology, University of Michigan, 1500 East Medical Center Drive, Ann Arbor, Michigan USA, 48109-5326

- Department of Radiology, Kantonsspital Baden, Im Ergel, Baden Switzerland 5404

*Corresponding author: Olaf Magerkurth, Department of Radiology, Kantonsspital Baden, Im Ergel,Baden Switzerland 5404

Received: December 31, 2020; Accepted: January 25, 2021; Published: February 01, 2021

Abstract

Purpose: In our department, we routinely perform Computed Tomography (CT) or Magnetic Resonance Imaging (MRI) of the lower extremity to assess femoral torsion for preoperative planning prior correcting osteotomies. It might be difficult to assess the FA, because on axial images the depicted part of the femoral neck is too short to allow correct alignment of the axis of the femoral neck. Measurements can also be performed on oblique axial images with improvement of depiction of the femoral neck but are smaller than those of measurements on axial images, due to the fact that images depend on rules of trigonometry. The aim is to provide a trigonometrical formula to calculate the value for FA, allowing precise assessment of femoral anteversion on oblique axial images similar to those on axial images.

Materials and Methods: Trigonometrical transformation is performed in three steps. Initial measurement of femoral anteversion on oblique images is transformed via a corresponding rectangular triangle from coronal images to calculated femoral anteversion on axial images.

Results: The first triangle is labelled with a1, b1, c1 for the sides and alpha1, beta1for the angles. Second and third triangle is labelled correspondingly. Length of both cathetus a1 and b1 are calculated as follows: cathetus a1=sin alpha1*c1 and cathetus b1=cos alpha 1*c1. Cathetus b2 is calculated as follows: b2=cos alpha2*c2. alpha3=tan-1 (a3/b3). Initial calculation of angle alpha3=tan-1 (a3/b3)=tan-1 (a1/b2), with a3=a1=sin alpha1*c1 and b3=b2=cos alpha2*b1*c, with b1=cos alpha1*c1 and b3=cos alpha2*cos alpha1*c1². The final formula is then: alpha3=tan-1 ((sin alpha1*c1)/(cos alpha²*cos alpha1*c12)) = tan-1 ((sin alpha1/(alpha2*cos alpha1*c1))

Conclusion: In this study we can provide a formula: alpha3=tan-1 ((sin alpha1/(cos alpha2*cos alpha1*c1)), which allows to calculate the femoral anteversion for true axial reconstructed images with the increased accuracy of measurements on oblique images and the ability to use the already known reference values from the literature.

Keywords: Femoral torsion; Imaging; MRI; CT

Introduction

Abnormal torsion of the femur can lead to a disturbed gait [1,2] and early onset osteoarthritis [3,4] with pain and diminished quality of life [5-7]. It can be treated surgically with osteotomies [1,4,5,8]. Computed Tomography (CT) or Magnetic Resonance Imaging (MRI) of the lower extremity is routinely performed to assess femoral torsion for preoperative planning prior correcting osteotomies [9-11]. Initially the anteversion of the Femoral Neck (FA) was assessed with radiographs by an anteroposterior view of the pelvis and a Dunn view where the Collum Diaphysis Angle (CCD) and projected femoral anteversion were measured and true FA was calculated [12,13]. Later Strecker et al. proposed the use of CT to measure Femoral Torsion (FT) [9]. In this method the FA and the rotation of the femoral condyles is measured on axial images and FT is calculated. Normal values could be established in a large patient group of 505 [9]. In patients with larger CCD angles it might be difficult to assess the FA, because on axial images the depicted part of the femoral neck is too short to allow correct alignment of the axis of the femoral neck [10,14]. In studies by Tomczak et al., and Schneider et al., measurements for the femoral neck were performed on oblique axial images with improvement of depiction of the femoral, neck and measurements of FA were considered to be more accurate [10,14]. But the values for FA were smaller than those of the classic measurement introduced by Strecker et al., [10,14]. This is due to the fact that images in MRI or CT are also projections and depend on rules of trigonometry, already shown by Sutter et al., who transformed measurements of femoral anteversion from oblique images to axial projections and tried to establish normal values for FA and FT on oblique axial images [15]. The hypothesis of our study is that we can provide a trigonometrical formula to calculate the value for FA, equivalent to those on axial images from measurements on oblique axial images and coronal scout images. The aim of the study is to allow precise assessment of femoral anteversion on oblique axial images without the need to establish new normal values.

Methods and Material

Institutional Review Board approval was waived due to the technical aspects of the study. For illustrational purpose three wooden models of the proximal femur with true CCD angles of 120°, 130° and 150° were built. To simulate anteversion also three wedges were built with 10°, 20° and 30° increment. All models were scanned with a CT scanner (Siemens Healthineers). Each data set consists of scout images and reconstructed images in true axial orientation and oblique images aligned to the CCD angle of each model.

To illustrate the path of trigonometrical transformation of the anteversion of the femoral neck on oblique images to anteversion on true axial images is divided into three steps. Angles are measured between the axis of the femoral neck through the center of the femoral head and a horizontal. The first triangle (Figure 1) is defined by the projected increment of axis of the femoral neck, and the length of the femoral neck on oblique images. The measurement of length of the femoral neck is performed similar to the measurement of Strecker et al., from the center of the femoral neck along the axis of the femoral neck to the line connecting the anterior and posterior outline of the lesser trochanter [9]. The second triangle (Figure 2) is defined by the measurement of the projected CCD angle on true coronal scout images and calculated values for the other two angles and sides of the triangle. The third triangle (Figure 3) represents the triangle on true axial images defined by the projected increment of the femoral neck, the projected length of the femoral neck and the height of the center of the femoral head, and is calculated of values from the first and second triangle. The connection of these three triangles is demonstrated (Figure 4).

Figure 1: The first triangle is aligned along the axis of the femoral neck. The sides of the first triangle are labeled with a1 and b1 for the cathetus und c1 for the hypotenuse. The corresponding angles are alpha1 and beta1. The femoral neck axis and length is equal to hypotenuse c1 and increment is angle alpha1.

    

    
    

    

    Figure 1: The first triangle is aligned along the axis of the femoral neck. The
sides of the first triangle are labeled with a1 and b1 for the cathetus und c1
for the hypotenuse. The corresponding angles are alpha1 and beta1. The
femoral neck axis and length is equal to hypotenuse c1 and increment is
angle alpha1.

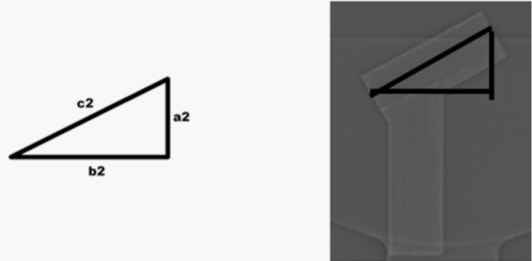
Figure 2: The second triangle is orientated similar to an anteroposterior view on x-ray. The sides of the second triangle are labeled with a2 and b2 for the cathetus and c2 for the hypotenuse. The corresponding angles are alpha2 and beta2. The projected CCD angle is measured on the scout image. This angle minus 90° is alpha2 in the second triangle.

    

    
    

    

    Figure 2: The second triangle is orientated similar to an anteroposterior view
on x-ray. The sides of the second triangle are labeled with a2 and b2 for the
cathetus and c2 for the hypotenuse. The corresponding angles are alpha2
and beta2. The projected CCD angle is measured on the scout image. This
angle minus 90° is alpha2 in the second triangle.

Figure 3: The third triangle is aligned along the true axial orientation. The sides of the triangle are labeled with a3 and b3 for the cathetus and c3 for the hypotenuse. The corresponding angles are alpha3 and beta3. Femoral anteversion similar to true axial images is represented by alpha3.

    

    
    

    

    Figure 3: The third triangle is aligned along the true axial orientation. The
sides of the triangle are labeled with a3 and b3 for the cathetus and c3 for
the hypotenuse. The corresponding angles are alpha3 and beta3. Femoral
anteversion similar to true axial images is represented by alpha3.

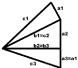
Figure 4: Combination of all 3 triangles: The triangle on top is the first triangle. In the middle is triangle 2 and at the bottom is triangle 3. The cathetus b1 of the first triangle is equal to the hypotenuse c2 of the second triangle. Cathetus a3 is equal to a1 and cathetus b2 is equal to cathetus b3. This figure also shows that the femoral length c1 measured on oblique axial images is different to the femoral length c3 measured on true axial images.

    

    
    

    

    Figure 4: Combination of all 3 triangles: The triangle on top is the first
triangle. In the middle is triangle 2 and at the bottom is triangle 3. The
cathetus b1 of the first triangle is equal to the hypotenuse c2 of the second
triangle. Cathetus a3 is equal to a1 and cathetus b2 is equal to cathetus b3.
This figure also shows that the femoral length c1 measured on oblique axial
images is different to the femoral length c3 measured on true axial images.

Results

With the CT data sets, the influence of rotation on the projected CCD angle is shown. For the model with a true CCD angle of 120° the projected CCD angle can range from 120° to 180° in different views from perpendicular to parallel to the femoral neck. In the model with a true CCD angle of 150° the projected angle can range from 150° to 180° (Figure 5). The influence of the orientation of reconstructed planes on the measured increment/anteversion of the femoral neck is demonstrated in (Figure 6). It is lower on oblique images than on true axial images. The transformation of values from oblique axial images to those of true axial images by using trigonometry in right-angled triangles can be divided into three steps.

Figure 5: Dependence of CCD angle due to rotation: Three-dimensional volume rendering of wooden models show dependence of projected Collum Diaphysis Angle (CCD) to viewing angle. A: Wooden model with 120° CCD. The viewing angle is perpendicular to the surface of the femoral neck. Thus the projected CCD is equal to the true CCD of 120°. B: In the same model, the viewing angle is now along the femoral neck and the projected CCD is 180°. C and D: Showing the same effect for a wooden model with a CCD of 140°

    

    
    

    

    Figure 5: Dependence of CCD angle due to rotation: Three-dimensional
volume rendering of wooden models show dependence of projected Collum
Diaphysis Angle (CCD) to viewing angle.
A: Wooden model with 120° CCD. The viewing angle is perpendicular to the
surface of the femoral neck. Thus the projected CCD is equal to the true
CCD of 120°.
B: In the same model, the viewing angle is now along the femoral neck and
the projected CCD is 180°.
C and D: Showing the same effect for a wooden model with a CCD of 140°

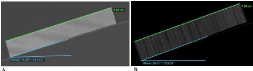
Figure 6: Dependence of anteversion from oblique to axial: Multiplanar reconstructions of a wooden model with known length of the femoral neck of 10cm and a CCD of 120°. The model was scanned on a wedge with an anteversion of 20°. A: shows the reconstructed plane in oblique orientation along the axis of the femoral neck. Length is 10 cm and similar to the true length, the projected anteversion is with 15° lower than the true anteversion. B: shows the reconstructed plane in true axial orientation of the same wooden model from the same CT scan. The projected length is with 8 cm shorter than the true length. The anteversion is 20° and similar to the anteversion of the wedge.

    

    
    

    

    Figure 6: Dependence of anteversion from oblique to axial: Multiplanar
reconstructions of a wooden model with known length of the femoral neck
of 10cm and a CCD of 120°. The model was scanned on a wedge with an
anteversion of 20°.
A: shows the reconstructed plane in oblique orientation along the axis of the
femoral neck. Length is 10 cm and similar to the true length, the projected
anteversion is with 15° lower than the true anteversion.
B: shows the reconstructed plane in true axial orientation of the same wooden
model from the same CT scan. The projected length is with 8 cm shorter than
the true length. The anteversion is 20° and similar to the anteversion of the
wedge.

A) The sides of the first triangle are labeled with a1 and b1 for the cathetus und c1 for the hypotenuse. The corresponding angles are alpha1 and beta1 (Figure 1). The femoral neck axis is equal to hypotenuse c1 and increment is angle alpha1. Length of both cathetus a1 and b1 are calculated as follows: cathetus a1=sin alpha1*c1 and cathetus b1=cos alpha 1*c1

B) The sides of the second triangle are labeled with a2 and b2 for the cathetus and c2 for the hypotenuse. The corresponding angles are alpha2 and beta2 (Figure 2). The cathetus b1 of the first triangle is equal to the hypotenuse c2 of the second triangle (Figure 2). The projected CCD angle is measured on the scout image. This angle minus 90° is alpha2 in the second triangle (Figure 2). Cathetus b2 is calculated as follows: b2 = cos alpha2*c2.

The hypotenuse c2 of the second triangle is equal to the cathetus b1 of the first triangle: c2=b1. And b1=cos alpha 1*c. The angle alpha2 =CCD-90°. We can replace c2 and b1 as follows: b2=cos alpha2*c2=cos alpha2*b1 and finally b2=cos alpha2*cos alpha 1*c1

C) The sides of the third triangle are labeled with a3 and b3 for the cathetus and c3 for the hypotenuse. The corresponding angles are alpha3 and beta3 (Figure 3). Cathetus a3 is equal to a1 and cathetus b3 is equal to b2. Femoral anteversion similar to true axial images is represented by alpha3 (Figure 3). The tan alpha3=a3/b3. The angle alpha3 is then calculated as follows:

alpha3=tan-1 (a3/b3)

The cathetus a3 is equal to a1 and cathetus b3 is equal to b2. We can replace a3 and b3 as follows: alpha3=tan-1 (a1/b2)

After condensing the three steps into one formula, the femoral anteversion on axial images can be calculated from the measurement of the length of the femoral neck on oblique images, the anteversion of the femoral neck on oblique images and the projected CCD angle on scout images as shown.

Initial calculation of angle alpha3=tan-1 (a3/b3) = tan-1 (a1/b2)

a3=a1= sin alpha1*c1

b3=b2=cos alpha2*b1*c1

with b1=cos alpha1*c1

b3=cos alpha2*cos alpha1*c1²

The final formula is then:

alpha3=tan-1 ((sin alpha1*c1)/(cos alpha2*cos alpha1*c1²))

= tan-1 ((sin alpha1/(cos alpha2 * cos alpha1 * c1))

In this formula, alpha1 is the measured anteversion of the femoral neck on oblique images. Alpha2 is the measured CCD angle minus 90°. C1 is the measured length of the femoral neck. When using this formula it is necessary to know that the value of tangens always represents 2 angles. One smaller 90° and one larger 90°. When using a calculator or inserting the formula into a table calculating program it is necessary to define the range from 0-90° to get the correct result.

Discussion

There are numerous causes for abnormal torsion of the femur [16,17]. Abnormal torsion can lead to gait disturbances, pain and early osteoarthritis [1-7]. We routinely perform MRI or CT to assess femoral torsion. This method was introduced by Strecker et al., where the anteversion of the femoral neck and of the femoral condyles is measured, and femoral torsion can be calculated. With this method there are well established normal values allowing the diagnosis of increased or decreased femoral torsion [9]. These measurements help orthopeadic surgeons to plan correcting osteotomies [4,5,9,13,16]. Since introduction of measurements of the femoral torsion the high inter-observer variability is discussed [10,11,14,15]. This may be due to the fact, that in patients for example with coxa valga, who have large CCD angles, the depicted portion of the femoral neck is short and correct measurement of the axis is difficult to achieve. This is especially true in children and adolescent patients, since the CCD angle decreases with age from 150° to 130° [18,19]. Tomczak et al., and Schneider et al., introduced a variation of assessing the femoral neck, by using oblique axial images of the femoral neck in MRI [10,14]. In these studies it was possible to depict the whole femoral neck on one image and to increase interobserver reliability of measurements of the femoral neck anteversion [10,14]. The authors also noticed an overall decrease of the femoral anteversion in their study population [10,14]. This was considered to be a bias of the patient group and lastly remained incompletely explained [10,14]. We assume that in this study the effects of trigonometry were underestimated. As we could show in our wooden models these effects cannot be neglected. Depending on the viewing angle, the visible angle can range from the true CCD angle to a maximum of 180° (Figure 5). This is also true for the measurement of the anteversion of the femoral neck on oblique images and axial images on the same model with the same true anteversion (Figure 6). In our opinion, a transformation of measurements on oblique images to values on axial images would be helpful, because there are well-established reference values in large patient groups allowing comparison of measurements on oblique images with these reference values. Thus, establishment of new references could be omitted. In a study by Sutter et al., the trigonometrical transformation of measurements of the femoral anteversion from oblique to axial images was performed [15]. Sutter et al., tried to establish normal values for measurements on oblique images. But the patient group was smaller than those in prior studies. In their study, the final formula to calculate the anteversion does not contain the length of the femoral neck. This is in contrast to our results where the length is necessary to calculate the femoral anteversion on true axial images. In this study we can provide a formula: alpha3=tan-1 ((sin alpha1/(cos alpha2*cos alpha1*c1)), which allows to calculate the femoral anteversion for true axial reconstructed images with the increased accuracy of measurements on oblique images and the ability to use the already known reference values from the literature.

References

  1. Gruskay JA, Fragomen AT, Rozbruch SR. Idiopathic Rotational Abnormalities of the Lower Extremities in Children and Adults. JBJS Rev. 2019; 7: e3.
  2. Ejnisman L, Philippon MJ, Lertwanich P, Pennock AT, Herzog MM, Briggs KK, et al. Relationship between femoral anteversion and findings in hips with femoroacetabular impingement. Orthopedics. 2013; 36: e293-e300.
  3. Terjesen T, Benum P, Anda S, Svenningsen S. Increased femoral anteversion and osteoarthritis of the hip joint. Acta Orthop Scand. 1982; 53: 571-575.
  4. Weidow J, Tranberg R, Saari T, Karrholm J. Hip and knee joint rotations differ between patients with medial and lateral knee osteoarthritis: gait analysis of 30 patients and 15 controls. J Orthop Res Off Publ Orthop Res Soc. 2006; 24: 1890-1899.
  5. Imhoff FB, Cotic M, Liska F, Dyrna FGE, Beitzel K, Imhoff AB, et al. Derotational osteotomy at the distal femur is effective to treat patients with patellar instability. Knee Surg Sports Traumatol Arthrosc Off J ESSKA. 2019; 27: 652-658.
  6. Tonnis D, Heinecke A. Diminished femoral antetorsion syndrome: a cause of pain and osteoarthritis. J Pediatr Orthop. 1991; 11: 419-431.
  7. Gelberman RH, Cohen MS, Shaw BA, Kasser JR, Griffin PP, Wilkinson RH. The association of femoral retroversion with slipped capital femoral epiphysis. J Bone Joint Surg Am. 1986; 68: 1000-1007.
  8. Rutz E, Brunner R. The pediatric LCP hip plate for fixation of proximal femoral osteotomy in cerebral palsy and severe osteoporosis. J Pediatr Orthop. 2010; 30: 726-731.
  9. Strecker W, Keppler P, Gebhard F, Kinzl L. Length and torsion of the lower limb. J Bone Joint Surg Br. 1997; 79: 1019-1023.
  10. Schneider B, Laubenberger J, Jemlich S, Groene K, Weber HM, Langer M. Measurement of femoral antetorsion and tibial torsion by magnetic resonance imaging. Br J Radiol. 1997; 70: 575-579.
  11. Guenther KP, Tomczak R, Kessler S, Pfeiffer T, Puhl W. Measurement of femoral anteversion by magnetic resonance imaging--evaluation of a new technique in children and adolescents. Eur J Radiol. 1995; 21: 47-52.
  12. Rippstein J. [Determination of the antetorsion of the femur neck by means of two x-ray pictures]. Z Orthop Ihre Grenzgeb. 1955; 86: 345-360.
  13. Muller ME. [Proximal osteotomies of the femur in the treatment of hip disease]. Helv Chir Acta. 1956; 23: 296-301.
  14. Tomczak RJ, Guenther KP, Rieber A, Mergo P, Ros PR, Brambs HJ. MR imaging measurement of the femoral antetorsional angle as a new technique: comparison with CT in children and adults. AJR Am J Roentgenol. 1997; 168: 791-794.
  15. Sutter R, Dietrich TJ, Zingg PO, Pfirrmann CWA. Assessment of Femoral Antetorsion with MRI: Comparison of Oblique Measurements to Standard Transverse Measurements. AJR Am J Roentgenol. 2015; 205: 130-135.
  16. Silva MS, Fernandes ARC, Cardoso FN, Longo CH, Aihara AY. Radiography, CT and MRI of Hip and Lower Limb Disorders in Children and Adolescents. Radiogr Rev Publ Radiol Soc N Am Inc. 2019; 39: 779-794.
  17. Kahf H, Kesbeh Y, van Baarsel E, Patel V, Alonzo N. Approach to pediatric rotational limb deformities. Orthop Rev. 2019; 11: 8118.
  18. von Lanz T, Wachsmuth W. Praktische Anatomie: Ein Lehr- und Hilfsbuch der Anatomischen Grundlagen Arztlichen Handelns. 1955.
  19. Hefti F. Kinderorthopadie in der Praxis. Heidelberg: Springer Medizin. 2006.

Citation: Konig F, Rutz E, Jacobson JA, Falkowski AL and Magerkurth O. Femoral Torsion in CT: Why We Should Add Some Trigonometry. Austin J Radiol. 2021; 8(1): 1120.