
Review Article
Austin J Robot & Autom. 2015; 2(1): 1008.
A New Pricing Mechanism for Uplink Power Control in Wireless Data Networks
Chuan L¹* and Lin W²
¹The Electronic 10th Institute of China Electronics Technology Group Corporation, China
2Department of Automation, Shanghai Jiao Tong University, China
*Corresponding author: Chuan L, The Electronic 10th Institute of China Electronics Technology Group Corporation, China. Si Chuan Cheng Du, China
Received: November 09, 2015; Accepted: December 30, 2015; Published: December 31, 2015
Abstract
In this paper, we study the uplink power control problem of wireless data networks, where mobile users can transmit information to multiple base stations. We formulate such problem as a super-modular game, and propose a novel pricing mechanism through the integration of channel gain and the signal-tointerference ration (SIR). We develop some conditions to guarantee the Nash Equilibrium, and present some simulations to illustrate the effectiveness and fairness of the proposed mechanism.
Keywords: Power Control; Super-modular Game; SIR; Multicell Network
Introduction
The rapid development of wireless network makes the large-scale, high-speed data transmission possible, meanwhile raises a higher demand for the accuracy of the information transmission. Since all users use the same frequency band to transport information, one user’s signal may disturb the others’. Hence the study of how to coordinate the users to transport more effective information with their limited energy has attracted significant attention.
Goodman et al. [1-5] made use of pricing mechanisms to limit the competition in power control of multi-cell wireless data networks, where they utilized microeconomic utility theory to define the users’ payoffs and employed a pricing function based on the users’ power to punish users who get high SIR maliciously by increasing their power. By solving a multi-objective optimization problem on two kinds of base station assignment, both better utility and lower power were obtained compared to the methods without a pricing mechanism. Differing from Goodman’s work, Tamer Basar et. al [8-10] used an information theoretic approach to study the power allocation problem, where they define the user’s utility function via channel capacity. In [11], Mehdi Rasti proposed a new pricing scheme based on Tamer Basar’s one cell model, where the pricing function was linearly proportional to the SIR. By choosing a proper price, the proposed pricing scheme can satisfy the fairness requirement in an optimum manner. In [12], a cost function was proposed to ensure the equal SIR, which ensures all users could achieve their desired SIR with suitable cost.
In order to get the information collected more reliable, sometimes, users apply multiple base stations simultaneously to transmit their information. This will accelerate the consumption of node’s limited resources. Therefore, how to improve the efficiency of transmission with their limited resources becomes more challenge. In this paper, we consider the situation that nodes associating to two or more base stations and investigate the fairness of users’ payment to the network providers. Inspired by [11], we adopt the pricing mechanism that any user possessing more network resource should pay more, and furthermore make an improvement on the unit price paid by each user. Some conditions are developed to guarantee the Nash equilibrium, and some simulations are presented to show the effectiveness and fairness of the improved mechanism.
The rest part of the paper is organized as follows. We construct the game model of the non-cooperative power control in Section 2; propose the pricing function based on users’ SIR in Section 3. We compare our pricing mechanisms with existed linear pricing mechanisms in Section 4, and give a conclusion in Section 5.
System Model
Assume that there are N users and K base stations in a wireless CDMA data network. All users use the same frequency band to transport information, and therefore any one user’s signal can interference with others. Considering that users using different base stations may have different SIR, here we define the SIR of user j with base station i [5] as follows:
where G represents the process gain. hij is the channel gain of user j to base station i and p j is the power of user j.
is the accumulated interference of all the other users caused to user j, where. s 2 denotes the background noise.
Two issues will influence the users’ quality of service (QoS) when the base station is determined: one is SIR, and the other is the consumed power. We define the j-th user’s utility function with the base station i as follows [5]:
Where M is the information length of each frame, L is the effective information length of each frame (L<M), and R denotes the speed of the user in transferring data.
Game Model
In [1-5], Goodman et al. reduce the energy consumption and improve the user’s utility by taking advantage of some pricing mechanisms. Inspired by those pricing mechanisms, we use the following pricing model:
Whereλ is a constant.
Under the situation that users apply multiple base stations simultaneously to transmit their information, we propose the following optimization problem denoted as P1:
With the power-punishment mechanism, sometimes, users enjoying best network services pay the least, while users with the worst network resources pay the most. This might reduce the positivity of users to use the network service, and lead to a waste of network resources.
Notice that users’ QoS are related with their SIR. Therefore, we can define a pricing function that monotonically increases with SIR, and moreover the unit price is based on the user’s channel gain. Intuitively, in such a way distant users pay a lower price to obtain a poorer network experience, while closer users pay a higher price to acquire a better service such as high throughput and low delay. Hence, we define a new pricing function as illustrated in equations (5) and (6):
where βij is the unit price of user j to base station i.
Accordingly, a new optimization problem denoted as P2 is defined by:
The net utility functions of P1 and P2 are not quasi concave. Based on the super modular game in [13,14], we know that if the utilities of P1 and P2 satisfy the non decreasing differences (NDD) conditions, they will have NE.
Definition 1: A game is a super modular game if it satisfies the following two conditions:
1) All participants in the strategy space is a compact set;
Based on the above analysis, we have the following results:
Theorem 1: P1 exists a NE solution if
Proof: As 0= p j = pmax , all user’s strategy space are compact set. For the second condition, the second partial derivation of P1 is:
For inequality (8) we have
equivalently
make logarithmic on the both sides of the inequality (11),
Theorem 2: P2 exists a NE solution if
where
Proof: As 0= p j = pmax , all user’s strategy space are compact set. For the second condition, the second partial derivation of P2 is:
(12)
For inequality (12), we note that whenis monotonically increasing. We have
Take inequality (13) into (12) we have:
Make logarithmic on the both sides of the inequality (15),
When ij γ meets the conditions in (11) and (17), P1 and P2 are super modular game. Therefore P1 and P2 exists NE solution.
Simulation
In multi-cell CDMA data systems, we assume that all the base stations can correctly receive information, they are fixed frame size and there is no forward error correction. In the following simulations, there are 20 stationary users and 4 base stations. The channel gain utilizes a simple path loss model with a=0.097 and b=4 in this paper.
Let G=W/R and chooseλ =105.All the parameters are listed in Table 1.
M, total number of bits per frame
80
L, number of information bits per frame
64
R, chips transmission rate
bits/second
W, spread spectrum bandwidth
Hz
modulation
Non-Coherent FSK
max power
2 Watts
background noise(AWGN)
Watts
Table 1: Simulation Parameters.
Algorithm: Consider the non-cooperative power control games of P1 and P2, use iteration to strike the optimal power,
Step 1: set the initial values, p(0) = 0, t (0)= 1, e = 0.000001, pmax = 2, tmax = 500, k=1.
Step 2: calculate p(k) to fulfill equation (18) and (19):
Step 3: check if |pi(k) − pi(k − 1)| = e, if yes go to Step 5, otherwise, go to Step 4.
Step 4: t (k)=t(k-1)+1,check if t(k) = tmax, if yes go to Step 5, otherwise return to Step 2.
Step 5: end.
Figure 1 shows the deployments of base stations and nodes. Figure 2 illustrates the powers at the equilibrium, which shows that the pricing mechanism (5)-(6) enable lower power consumption than the linear power mechanism (3). Figure 3 shows the utilities at the equilibrium, which indicates that all users get higher utilities with the pricing mechanism (5)-(6) than the pricing mechanism (3).
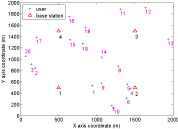
Figure 1: Nodes and base stations assignment.
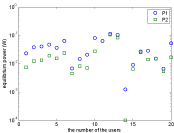
Figure 2: Equilibrium power.
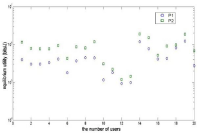
Figure 3: Equilibrium utility.
Figure 4 shows the prices at the equilibrium. From Figures 3 and 4, we can see that: Under the power pricing mechanism (3), users who obtain less utility usually pay more; while under the pricing mechanism (5)-(6), users with higher QoS should pay more. Therefore, the mechanism (5)-(6) improves the fairness, which can promote the users to participate in using the network effectively. This will reduce energy waste, improve network performance, and avoid network paralysis.
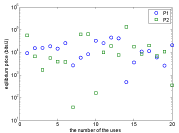
Figure 4: Equilibrium price.
Conclusions
In this paper, we consider a situation that nodes associate all base stations. Different from the classical linear power pricing mechanism, we introduce a pricing function based on users’ SIR and path gain to improve the fairness of utilization, so that users acquire more network resource should pay more. Simulations show that the pricing mechanism performs a better utility and lower power than the linear power pricing mechanism.
References
- Viral Shah, Narayan B, Mandayam, and David J. Goodman. Power Control for Wireless Data based on Utility and Pricing. In Proc. PIMRC. 1998: 1427-1432.
- Cem U Saraydar, Narayan B Mandayam and David J Goodman. Pareto Efficiency of Pricing-based Power Control in Wireless Data Networks, Wireless Communications and Networking Conference. 1999; 231-235.
- Cem U Saraydar, Narayan B Mandayam and David J Goodman. Efficient Power Control via Pricing in Wireless Data Networks. IEEE Transactions on Communications. 2002; 2: 291-303.
- David Famolari, Narayan Mandayam, David Goodman and Viral Shah. A New Framework for Power Control in Wireless Data networks: Games, Utility and Pricing, Wireless Multimedia Network Technologies R Ganesh et al. editors, Kluwer Academic Publishers. 2000: 289-310.
- Cem U Saraydar, Narayan B Mandayam and David J Goodman. Pricing and Power Control in a Multicell Wireless Data Network. IEEE J Select. Areas Commun. 2001; 19: 1883-1892.
- ShaoleiRen and Mihaela van der Schaar. Pricing and Distributed Power Control in Wireless Relay Networks. IEEE Transations on Signal Processing. 2011: 2913-2926.
- John Nash. "Non-cooperative Games." Publication Info. 1951.
- Tansu Alpcan, Tamer Basar, R Srikant and Eitan Altman. CDMA Uplink Power Control as a Non-cooperative Game. IEEE Conference on Decision and Control Orlando TuA 07-3. 2001: 197-202.
- Tansu Alpcan, Tamer Basar and R Srikant. CDMA Uplink Power Control as a Non-cooperative Game, Wireless Networks 8. 2002: 659-670.
- Tansu Alpcan, Tamer Basar and Subhrakanti. A Power Control Game Based on Outage Probabilities for Multicell Wireless Data Networks. IEEE Transaction on Wireless Communications. 2006; 5.
- Mehdi Rasti, Ahmad R. Sharafat and BabakSeyfe. Pareto-Efficient and Goal-Driven Power Control in Wireless Networks: A Game-Theoretic Approach With a Novel Pricing Scheme. IEEE/ACM Transactions on Networking 2009; 17: 556-569.
- Ehsan Pasandshanjani, Babak Hossein Khalaj and Mahyarshirvani Moghaddam. A new cost function for game theoretic sir-based power control algorithms. IWCMC. 2011: 1147-1151.
- DM Topkis. Equilibrium points in nonzero sum n-person sub modular games, SIAM J. Control and Optimization. 1979; 17: 773-787.
- Chuan Lai, Yiping Yang, Lin Wang and Xiaofan Wang. Power Control Based on Improved Pricing Mechanism in a CDMA Network. Journal of Computational information systems. 2012; 8: 8373-8380.