
Research Article
Austin J Surg. 2019; 6(24): 1228.
The Accuracy of Intraocular Lens Power Calculation Formulas for Eyes of Axial Length Smaller than 22.0mm
Stopyra W*
Ophthalmological Hospital MW med, Poland
*Corresponding author: Wiktor Stopyra, Ophthalmological Hospital MW med, Cracow, Poland
Received: September 19, 2019; Accepted: November 05, 2019; Published: November 12, 2019
Abstract
Purpose: Comparison of intraocular lens power calculation formulas’ accuracy for eyeballs shorter than 22.00mm.
Material and Methods: 56 patients (62 eyeballs) were examined, whose ocular axial length ranged between 20.58mm and 21.97mm. Preoperatively, the intraocular lens power for each patient was calculated using six different formulas (Holladay1, SRK/T, Hoffer Q, Holladay 2, Haigis and Barrett Universal II). The power of the implanted intraocular lens was based on the Hoffer Q formula. Three months after cataract surgery, postoperative refraction was measured. Mean absolute error as a difference between postoperative and predicted spherical equivalences of refractive error was calculated.
Results: The Hoffer Q formula achieved the lowest level of mean absolute error of 0.09 ± 0.08 D (p ‹ 0.001 for Hoffer Q versus each of the other formulas). Further places were taken by the following formulas: Barrett Universal II (0.19 ± 0.16 D), Holladay 2 (0.20 ± 0.13 D), Haigis (0.21 ± 0.22 D), SRK/T (0.23 ± 0.17 D), Holladay 1 (0.26 ± 0.17 D). P ‹ 0.05 for Haigis versus SRK/T and versus Holladay 2 formulas, as well as Holladay 2 versus Holladay 1 formula. Additionally, correlation between absolute error and axial length was evaluated. It was observed, that absolute error had been associated with axial length when Hoffer Q or SRK/T formula had been used.
Conclusions:
1. Hoffer Q formula is recommended for intraocular lens power calculation for eyeballs with an axial length shorter than 22.0mm.
2. Haigis formula seems to be satisfactory for these cases.
Keywords: Intraocular lens power calculation formula; Eyeball shorter than 22.0mm; Hoffer Q formula; Mean absolute error
Introduction
There are many intraocular lens (IOL) power calculation formulas. They form five generations [1]. They are divided into theoretical formulas and empirical ones. Theoretical (Fyodorov, Binkhorst, Hoffer) are based on geometrical optics of eye while empirical (SRK II, SRK/T, Haigis) are generated by averaging large numbers of postoperative clinical results. Usually most IOL power calculation formulas perform well for eyes of axial length (AL) between 22.0mm and 25.0mm [2]. In the cases when an eyeball is shorter than 22.0mm or longer than 25.0mm only some formulas give correct results [2-4].
Material
This study reviewed 62 cataract eyeballs from 56 patients (30 women and 26 men at the age of 55 to 92 years). Axial lengths of the eyeballs were in the range between 20.58mm and 21.97mm. Patients after retinal detachment and refractive surgery were excluded from this study.
Methods
Before cataract surgery, auto refracto keratometer was used for corneal power measurement. AL was measured by IOLMaster 700 as well as IOL power was calculated according to six different formulas (Holladay 1, SRK/T, Hoffer Q, Haigis, Holladay 2, Barrett Universal II). Each cataract surgery was performed by the same doctor. Only acrylic foldable intraocular lenses with power calculated according to the Hoffer Q formula were implanted. Postoperative refraction was measured 3 months after cataract surgery. Mean absolute error (MAE) as a difference between postoperative and predicted spherical equivalences of refractive error was calculated.
Statistical analysis was performed using the Statistica 13.1 package.
Results
The Hoffer Q formula achieved the lowest level of MAE 0.09±0.08 D. Detailed results of the calculated absolute error for each formula were summarized using descriptive statistics (mean, standard deviation, median and range) and were collected in Table 1 & Figure 1.
Absolute error
SRK/T
Hoffer Q
Holladay 1
Haigis
Holladay 2
Barrett Universal
Average±SD
0.23±0.17
0.09±0.08
0.26±0.17
0.21±0.22
0.20±0.13
0.19±0.16
Median
0.20
0.06
0.23
0.13
0.19
0.14
Min-max
0.01-0.63
0.00-0.34
0.01-0.73
0.00-0.91
0.00-0.54
0.00-0.71
Table 1: Descriptive statistics of absolute error.
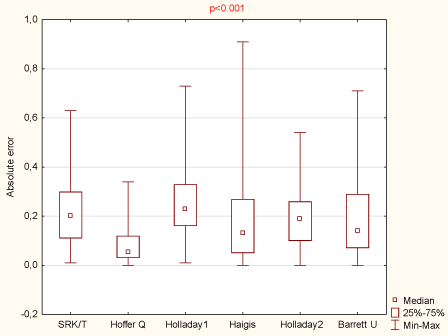
Figure 1: Descriptive statistics of absolute error.
The nonparametric Kruskal-Wallis test was performed to compare absolute error (AE) scores according to six formulas. The results were considered statistically significant if the p-value was less than 0.05 (p ‹ 0.05). The obtained probability value was p ‹ 0.001 (lower than the assumed significance level a = 0.05) therefore it was checked between which pairs of formulas there were statistically significant differences. For this purpose, the nonparametric U-Mann-Whitney test was performed. Due to multiple comparisons, Bonferroni corrections were applied and that was why the significant level was assumed to be a = 0.05/15 = 0.003. For variables Hoffer Q versus each other formulas as well as Haigis versus Holladay 2 and versus SRK/T formulas and for Holladay 2 versus Holladay 1 formula statistically significant differences were founded. The results were shown in Table 2.
U-Mann-Whitney test results
p
SRK/T vs Hoffer Q.
<0.001
SRK/T vs Holladay 1
0,296
SRK/T vs Haigis
0.039
SRK/T vs Holladay 2
0.497
SRK/T vs Barrett Universal.
0.108
Hoffer Q vs Holladay 1
<0.001
Hoffer Q vs Haigis
<0.001
Hoffer Q vs Holladay 2
<0.001
Hoffer Q vs Barrett Universal.
<0.001
Holladay 1 vs Haigis
0.313
Holladay 1 vs Holladay 2
0,004
Holladay 1 vs Barrett Universal.
0.069
Haigis vs Holladay 2
0.013
Haigis vs Barrett Universal.
0.512
Holladay 2 vs Barrett Universal.
0.299
Table 2: U-Mann-Whitney test results for each pair of formulas.
Additionally, correlation between AL and AE was evaluated. The results of Spermann rank correlation between AE and AL for each of the six formulas are presented in Table 3.
Variables
Formula
N
R
t(N-2)
p
AL & AE
SRK/T
62
0,321
2,623
0,011
AL & AE
Hoffer Q
62
-0,329
-2,700
0,009
AL & AE
Holladay 1
62
0,033
0,256
0,799
AL & AE
Haigis
62
0,047
0,361
0,720
AL & AE
Holladay 2
62
-0,136
-1,059
0,294
AL & AE
Barrett Univ.
62
0,122
0,953
0,345
Table 3: Spermann rank test results.
Statistically significant correlation factors occur between AE and AL for the SRK/T formula as well as for the Hoffer Q formula. Both correlations are low. Detailed correlation charts are presented in Figures 2 & 3.
Figure 2 Correlation between absolute error and axial length for the Hoffer Q formula.
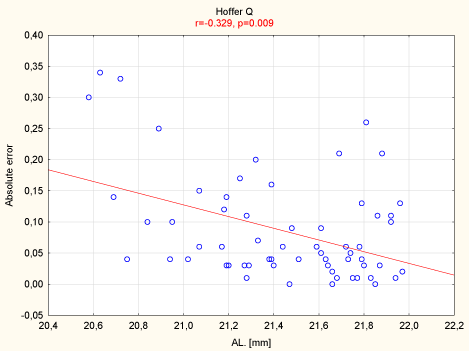
Figure 2: Correlation between absolute error and axial length for the Hoffer
Q formula.
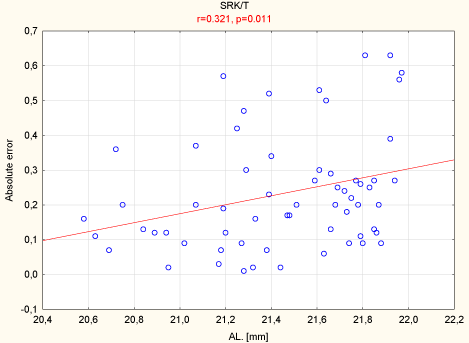
Figure 3: Correlation between absolute error and axial length for the SRK/T
formula.
Discussion
It is most important to obtain good postoperative refractive results for cataract surgery [2]. Obviously, it depends on the properly selected IOL power calculation formula especially for eyes shorter than 22.0mm [5]. The meta-analysis of 1161 eyeballs shorter than 22.0mm published in 2018 showed the superiority of the Haigis formula over Hoffer Q, SRK/T and SRK II formulas [3]. The highest accuracy of the Haigis formula was also shown by a study carried out by Batkov et al. as well as by Moschos, Chatziralli and Koutsandrea [6,7]. Roh et al. came to a similar conclusion in their 2011 study [8]. In turn, Hoffer and Savini showed that Haigis, Hoffer Q, and Holladay 2 formulas were the best options for IOL power prediction in short eyes [5]. However, Carifi et al. demonstrated that the Hoffer Q formula was the most accurate in prediction IOL power and did not notice the difference in the accuracy of Holladay 1, Haigis, and Holladay 2 formulas for eyes smaller than 22.0mm [9]. In turn, Doshi et al. equally well evaluated Hoffer Q, Holladay 1 and SRK/T formulas in predicting the postoperative refraction after cataract surgery for eyes of AL less than 22.0mm [10]. In my 2017 study, I showed the greatest accuracy of the Hoffer Q formula but I did not consider Holladay 2 or Barrett Universal II formulas at the time [11]. Gökce et al. came to interesting conclusions in their study. They proved that Hoffer Q and Holladay 2 formulas gave slightly myopic refractive prediction errors while the Olsen formula hyperopic ones [12]. Additionally, they did not observe any statistically significant differences in the MAE between Holladay 1, Haigis, Hoffer Q, Olsen, Barrett Universal II, Holladay 2 and Hill RBF formulas when the mean numerical refractive prediction error was adjusted to zero [12]. In turn, Karabela, Eliacik and Kava showed good results of IOL power calculation using the SRK/T formula [13]. However, Szaflik et al. did not recommend using SRK/T and SRK II formulas for short eyeballs [14]. They rather suggested Hoffer Q or Holladay formulas [14]. Nevertheless, Aristodemou et al. in their research with 8108 eyes proved that the Hoffer Q formula used for calculating the IOL power for eyes with AL between 20.0mm and 20.99mm gave the best results, whereas Hoffer Q and Holladay 1 formulas were the most precise ones for eyes with AL longer than 21.00 but shorter than 21.49mm [15].
As can be seen, there is no single IOL power calculation formula in cases of short eyeballs. Most often the Hoffer Q formula is considered as the best one [5,9-12,14,15]. The Haigis formula also gave very good results in IOL power calculation for eyeballs with AL smaller than 22.0mm [3,5-8]. Similar conclusions gave my study. The Hoffer Q formula gave the smallest result of AE as both an average as a median. The Haigis formula obtained the second results as a median.
Conclusions
1. The Hoffer Q formula is recommended for IOL power calculation for eyeballs with AL smaller than 22.0mm.
2. The Haigis formula seems to be satisfactory for these cases.
References
- Stopyra W. The accuracy of IOL power calculation formulas for eyes of axial length exceeding 24.5mm. Klin Oczna. 2013; 115: 93-95.
- Chen C, Xu X, Miao Y, Zheng G, Sun Y, Xu X. Accuracy of Intraocular Lens Power Formulas Involving 148 Eyes with Long Axial Lengths: A Retrospective Chart-Review Study. J Ophthalmol. 2015; 2015: 976847.
- Wang Q, Jiang W, Lin T, Wu X, Lin H, Chen W. Meta-analysis of accuracy of intraocular lens power calculation formulas in short eyes. Clin Exp Ophthalmol. 2018; 46: 356-363.
- Wang Q, Jiang W, L in T, Zhu Y, Chen C, Lin H. Accuracy of intraocular lens power calculation formulas in long eyes: a systemic review and metaanalysis. Clin Exp Ophthalmology. 2018; 46: 738-749.
- Hoffer KJ, Savini G. IOL power calculation in short and long eyes. Asia Pac J Ophthalmol (Phila). 2017; 6: 330-331.
- Batkov E, Pashtayev N, Mikhaylova V. Calculation of intraocular lens power in surgical treatment of extreme hyperopia. Vestn Oftalmol. 2019; 135: 21-27.
- Moschos M, Chatziralli I, Koutsandrea C. Intraocular lens power calculation in eyes with short axial length. Indian J Ophthalmol. 2014; 62: 692-694.
- Roh Y, Lee S,Han Y, Kim M, Wee W, Lee J. Intraocular lens power calculation using IOL Master and various formulas in short eyes. Korean J Ophthalmol. 2011; 25: 151-155.
- Carifi G, Aiello F, Zygoura V, Kopsachilis N, Maurino V. Accuracy of the refractive prediction determined by multiple currently available intraocular lens power calculation formulas in small eyes. Am J Ophthalmol. 2015; 159: 577-583.
- Doshi D, Limdi P, Parekh N, Gohil N. A Comparative Study to Assess the Predictability of Different IOL Power Calculation Formulas in Eyes of Short and Long Axial Length. J Clin Diagn Res. 2017; 11: NC01-NC04.
- Stopyra W. Accurate intraocular lens power calculation formulas for eyeballs with the axial length smaller than 22.0mm. Okulistyka 3/2017: 29-31.
- Gökce S, Zeiter J, Weikert M, Koch D, Hill W, Wang L. Intraocular lens power calculation in short eyes using 7 formulas. J Cataract Refract Surg. 2017; 43: 892-897.
- Karabela Y, Eliacik M, Kava F. Performance of the SRK/T formula using A-Scan ultrasound biometry after phacoemulsification in eyes with short and long axial lengths. BMC Ophthalmol. 2016; 16: 96.
- Szaflik J, Kaminska A, Gajda S, Jedruch A. Accuracy of the SRK II, SRK/T, Holladay and Hoffer Q IOL power calculation formulas in hyperopic patients after phacoemulsification. Klin Oczna. 2005; 107: 615-619.
- Aristodemou P, Knox Cartwright N, Sparrow J, Johnston R. Formula choice: Hoffer Q, Holladay 1 or SRK/T and refractive outcomes in 8108 eyes after cataract surgery with biometry by partial coherence interferometry. J Cataract Refract Surg. 2011; 37: 63-71.