Numerical Studies about the Multi-Layered Textile Composite Reinforcement Forming

    

    

    Figure 1:  Multi-scales in the numerical modelling of composite forming.
    
    

As an alternative approach to the macroscopic and mesoscopic approaches, a semi-discrete approach has been developed in [13,23]. This semi-discrete shell finite element is comprised of unit woven cells with rotation free, which presents only displacements of nodal variables. The warp and weft directions of the woven fabric can be in an arbitrary direction with respect to the direction of the element side. Comparing to the discrete approach, the computational cost is reduced significantly due to the decrease in the number of Degree of Freedom (DOF). Regarding the continuous approach, the semidiscrete approach avoids the use of stress tensors and defines directly the loading on a woven unit cell by the warp and weft tensions and by in-plane shear and bending moments [13,23]. In this case, it does not need to determine and update the particular homogenous behaviour of textile materials to employ in a continuous model.

The virtual work theorem is described in Equation (1) for any virtual displacement ñ (ñ field is equal to zero on the boundary with prescribed displacements Гu). The internal virtual work is assumed to be composed of three terms (Equation (2)): the work connected to fibre biaxial tensions, the work due to in-plane shear presenting the variation of the angle between warp and weft directions, the work corresponding to bending effects during a flexion of the fabric.

$w_{ext}(\overline{\eta })-w_{\mathrm{int}}^{}(\overline{\eta })=w_{acc}^{}(\overline{\eta })$ $\forall \overline{\eta }/\overline{\eta }=0$ on ${\Gamma }_u$ (1)

With

$w_{\mathrm{int}}(\overline{\eta })=w_{\mathrm{int}}^t(\overline{\eta })+w_{\mathrm{int}}^s(\overline{\eta })+w_{\mathrm{int}}^b(\overline{\eta })\text{ (2)}$

where int wt (η ) , int ws (η ) and int wb (η ) are the virtual internal works of tension, in-plane shear and bending, respectively, with:

$w_{\mathrm{int}}^t(\overline{\eta })={\displaystyle \sum _{P=1}^{ncell}{}^P\epsilon {}_{11}(\overline{\eta })}\cdot {}^{P}T{}^{11}\cdot {}^{P}L{}_1+{}^P\epsilon {}_{22}(\overline{\eta })\cdot {}^{P}T{}^{22}\cdot {}^{P}L{}_2\text{ (3)}$

$w_{\mathrm{int}}^t(\overline{\eta })={\displaystyle \sum _{P=1}^{ncell}{}^P\gamma (\overline{\eta })}\cdot {}^{P}M{}^s$ (4)

$w_{\mathrm{int}}^t(\overline{\eta })={\displaystyle \sum _{P=1}^{ncell}{}^P\chi {}_{11}(\overline{\eta })}\cdot {}^{P}M{}^{11}\cdot {}^{P}L{}_1+{}^P\chi {}_{22}(\overline{\eta })\cdot {}^{P}M{}^{22}\cdot {}^{P}L{}_2$ (5)

where Ρ is the woven cell number, ncell is the total number of woven cells, ε₁₁ (η ) and ε₂₂ (η ) are the virtual biaxial strains, L₁ and L₂ are the length of unit woven cell in warp and weft directions, γ (η ) s the virtual angle between the warp and weft directions, is the in-plane shear moment, χ₁₁ (η ) and χ₂₂ (η ) are the virtual curvatures of warp and weft directions, M¹¹ and M²² are the bending moments on the woven cell following warp and weft directions.

The mechanical behaviour of the textile composite reinforcements during forming is given by the biaxial tensile properties [33-35], the in-plane shear properties [36-43] and the bending properties [18,44- 46]. These mechanical properties will be used in the following forming simulations presented in the section 4.

Surface Contact Management

As one of the key problems, the interactions of tool / ply and ply / ply should be taken into account in the numerical model. The geometric description of the surface contact is managed in a manner that we can work with a complex shell to shell contact problem, which can be composed classically in different contact cases: point / point, point / surface, point / segment, and segment / segment.

The numerical simulation of contact behaviour during the forming process is accomplished using the algorithm of the forward increment Lagrange multipliers proposed by Carpenter [24]. This method could be introduced into the dynamical expression described as Equation (6) as contact occurs. In which [M] is the mass matrix, {u&&} is acceleration vector, {Fint} and {Fext} are internal and external loads vectors of the system, {λ} is Lagrange multiplier vector and its components are the surface contact forces, n is an index of calculation step and [G] is a surface contact displacement constraint matrix.

$[M]\left\{{\ddot{u}}_n\right\}+\left\{F_n^{\mathrm{int}}\right\}+{[G_{n+1}]}^T\left\{{\lambda }_n\right\}=\left\{F_n^{ext}\right\}$ (6)

$[G_{n+1}](\{u_{n+1}\}+\{X_0\})=\left\{0\right\}$ (7)

Where {u} is the vector of displacement degrees of freedom and {X_o} is the material co-ordinate vector.

In the case of “semi-implicit” integration, the total displacement of each node can be calculated according to Equation (8) by a predictor {u*}, determined from Equation (6) under the condition without contact effect and a corrector {uc}, computed as the contact loads presented (see Figure 2).

$\begin{array}{l}\left\{u_{n+1}\right\}=\left\{u_{n+1}^{*}\right\}+\left\{u_{n+1}^c\right\}\\ \left\{u_{n+1}^{*}\right\}=\Delta t^2{[}^M(\{F_n^{ext}\}-\{F_n^{\mathrm{int}}\})+2\left\{u_n\right\}-\left\{u_{n-1}\right\}\\ \left\{u_{n+1}^c\right\}=-\Delta t^2{[}^M{[}^{G_{n+1}}\left\{{\lambda }_n\right\}\end{array}$ (8)

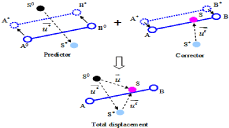
Figure 2: Calculation of the total displacement by using a predictor and a corrector.

    

    

    Figure 2:  Calculation of the total displacement by using a predictor and a
corrector.
    
    

Close

where Δt is a time step increment.

After combine the equation (7) and (8), it leads to straightly a linear solution of contact forces shown in Equation (9). Subsequently, the calculations of contact forces increment and the corrector of the total displacement can be performed by using the Gauss-Seidel iteration algorithm [24].

$\Delta t^2[G_{n+1}^{}]{[M]}^{-1}{[G_{n+1}^{}]}^T\left\{{\lambda }_n^{}\right\}=[G_{n+1}^{}](\{u_{n+1}^{*}\}+\{X_0\})$ (9)

Forming Simulations and Experimental Correlation

In the numerical simulation model, the tensile, in-plan shear and bending behaviour laws are described as Equation 10, 11 and 12, respectively:

The tensile behaviour law: $T^{11}=C_1{\epsilon }_{11}$ and $T^{22}=C_2{\epsilon }_{22}$ (10)

where C₁ and C₂ are the tensile stiffnesses in warp and weft directions.

The in-plane shear behaviour law:

$M^s(\gamma )=k_1\gamma +k_2{\gamma }^3+k_3{\gamma }^5$ (11)

Where K₁, K₂ and K₃ are the in-plane shear stiffnesses.

The bending behaviour law : Mⁱⁱ =B_iX_ii (i=1, 2) (12)

where B1 and B2 are the bending stiffness in warp and weft directions.

The cylindrical preformings for the G1151® fabric manufactured by HEXCEL Corporation have been performed and shown in Figure 3. The dimensions of the fabric are 375 mm × 375 mm. The main mechanical properties of the G1151® fabric are given in Table 1. The punch radius is 37 mm. A weak blank holder pressure of 4.3×10-3 MPa are used in the preforming tests. The punch displaces vertically with a constant velocity of 30 mm/min and the maximum displacement is 50 mm.

Figure 3: The forming experiments by a cylinder punch for the G1151® fabric: (a) Experimental set-up, (b) With a single ply [0°/90°], (c) With a single ply [-45°/45°], (d) With two plies [0°/90°, 0°/90°], (d) With two plies [0°/90°, -45°/45°], (e) With tow plies [-45°/45°, 0°/90°].

    

    

    Figure 3:  The forming experiments by a cylinder punch for the G1151®
fabric: (a) Experimental set-up, (b) With a single ply [0°/90°], (c) With a single
ply [-45°/45°], (d) With two plies [0°/90°, 0°/90°], (d) With two plies [0°/90°,
-45°/45°], (e) With tow plies [-45°/45°, 0°/90°].
    
    

Close

Figure 3b and 3c show the deformed shape of a single ply with a fibre orientation of 0/90° and ±45°. The wrinkling phenomena are very different in these two forming cases due to the different fibre orientations. Figure 3d presents the forming with two 0/90° plies. As it has not relative fibre orientation in the preform stacking, the deformed preform after forming is identical to one of mono-ply forming shown in Figure 3b. When a relative fibre orientation presents in preform, e.g. in Figure 3e and 3f, the deformed shape of the preform and the wrinkling phenomena are modified. The material draw-in and the in-plane shear effects are not same during the 0/90° and ±45° plies. In addition, the interaction between two contact plies depends on the inter-ply friction, in this case the wrinkling phenomenon could be modified. It points out the important impact of the relative fibre orientation during the multi-layered textile reinforcement forming.

The forming simulations corresponding to the experimental preforming tests are shown in Figure 4. The coefficient of friction 0.2 on tool / ply and ply / ply surfaces is used in the forming simulation. Compared to the preforming test shown in Figure 3, a good agreement can be observed about the wrinkling phenomena between experimental approach and numerical simulation. When the two plies are superimposed in the same direction (see Figure 3d and 4d), the similar wrinkling phenomena can be observed compared to a single ply forming (Figure 3b and 4b). Moreover, it has no intersliding between the two plies. The inter-sliding was determined by the difference of material draw-in between the top and the bottom plies. The maximum material draw-in and inter-sliding are presented in Table 3. The similar measurements can be observed between experiment approach and forming simulation. The maximum drawin is noted at the central point of four sides of 0/90° ply and in the four corners of ±45° ply as observed in Figure 3 and 4. Compared to the draw-in between the [0°/90°] and [-45°/+45°] preforms, the draw-in of 0°/90° ply is always bigger than ±45° ply’s due to an increasing of friction effects between tool/ply and ply/ply. Furthermore, comparing the single-ply and multilayered forming by using the same yarn orientation, the maximum material draw-in is slightly important in the forming of a single ply as the friction coefficient was different on the contact surfaces tool/ply and ply/ply. Normally, the friction coefficient is bigger on the contact surface ply/ply than on the surface tool/ply.

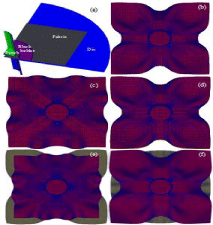
Figure 4: Numerical simulations of a cylindrical forming for G1151® fabric: (a) 1/4 geometry model and mesh structure, (b) with a single ply [0°/90°], (c) with a single ply [-45°/45°], (d) with two plies [0°/90°, 0°/90°], (e) with two plies [0°/90°, -45°/45°], (f) with tow plies [-45°/45°, 0°/90°].

    

    

    Figure 4:  Numerical simulations of a cylindrical forming for G1151® fabric:
(a) 1/4 geometry model and mesh structure, (b) with a single ply [0°/90°], (c)
with a single ply [-45°/45°], (d) with two plies [0°/90°, 0°/90°], (e) with two plies
[0°/90°, -45°/45°], (f) with tow plies [-45°/45°, 0°/90°].
    
    

Close

Numerical Analyses of Multilayered Textile Composites Forming

The properties of the woven composite reinforcement considered in two different following simulation examples are shown in Table 2. The speed of the forming in the simulation is larger than the real one but it is checked that the kinematical energy remains small enough to consider that the transformation is quasi-static.

“Double dome” forming process

According to the “double dome” forming in the international benchmark framework [47,48], the geometry of the tools are described in Figure 5. The coefficient of friction on the surface contacts is f = 0.3. A blank holder pressure 2×10-4 MPa is applied during the forming stage.

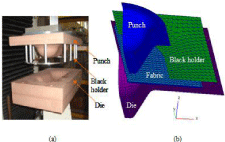
Figure 5: Numerical simulation of “double dome” forming process: (a) Experimental set-up, (b) ¼ Geometry model and mesh structure.

    

    

    Figure 5:  Numerical simulation of “double dome” forming process: (a)
Experimental set-up, (b) ¼ Geometry model and mesh structure.
    
    

Close

The forming simulation of eight woven plies with different fibre orientation is shown in Figure 6. The preform sequence is [0°/90°, -45°/45°, 0°/90°, -45°/45°]2 . As each ply is not placed in same orientation, the ply is deformed in different way during the forming. Consequently, the material draw-in and the in-plane shear angle are varied significantly by the change in fibre orientation [10]. The importance of fibre orientation is emphasized not only in the monoply composite forming but also in the multilayered one.

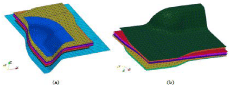
Figure 6: Numerical simulation of “double dome” forming with eight woven plies with different fibre orientation: (a) Preform stacking and forming tools, (b) Only preform stacking.

    

    

    Figure 6:  Numerical simulation of “double dome” forming with eight woven
plies with different fibre orientation: (a) Preform stacking and forming tools,
(b) Only preform stacking.
    
    

Close

Forming with a cylindrical punch

As mentioned previously (in section 4), it often experiences the wrinkling phenomenon during the composite forming due to the strong in-plane shear effects. This phenomenon could be modified in the multilayered forming cases; particularly, it could be strengthened due to the interactions among the plies. A cylindrical forming (Figure 7) is presented to introduce this aspect. Figure 7 shows the geometry model. The punch radius is 156 mm. The dimensions of the fabric are noted in Table 2. A 0.1 MPa pressure is applied on the eight independent blank holders during the whole forming stage.

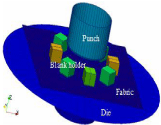
Figure 7: Geometry model and mesh structure of the cylindrical forming.

    

    

    Figure 7:  Geometry model and mesh structure of the cylindrical forming.
    
    

Close

As an essential forming parameter, the relative fibre orientation plays important roles in the multilayered composite forming, which could lead to a series remarkable modification of the deformed preform, e.g. the wrinkling phenomenon. Although it is not simple to conclude that the wrinkles increase with an increasing of the relative orientation between the plies (Figure 8), it can be observed that the more important wrinkling phenomenon presents in Figure 8c than Figure 8a and in Figure 8d than Figure 8b. It is clear that in the case of Figure 8d the wrinkling phenomenon is most important than the other cases due to the stronger variation of the relative fibre orientation between the plies.

Figure 8: Wrinkling phenomenon changes following the different sequence of the preforms stacking in the four woven layer cylindrical forming.

    

    

    Figure 8:  Wrinkling phenomenon changes following the different sequence of
the preforms stacking in the four woven layer cylindrical forming.
    
    

Close

Conclusion

It is important to predict the feasibility conditions of a multilayered composite forming process through the numerical simulation analyses. The forming simulation results can not only improve our understanding of the forming process but also give some essential forming information, such as the final shape of the preform, fibre positions and the wrinkling phenomena. An example of the correlation forming simulation/experimental preforming and the following numerical applications mentioned in this paper show a capacity of simulating the multilayered composite forming by the developed numerical model. The numerical simulation analysis demonstrates generally the multilayered aspect in the textile composite reinforcement forming. The results point out the significant importance of the relative fibre orientation between the layers and the inter-ply friction in multilayered forming.

forming simulations are confirmed by the forming experiments. The numerical and experimental data presents that in multilayered cases the wrinkles will be modified corresponding to the changes of the preform’s sequence, but they will not be changed if the ply is superposed with a same fibre orientation. The forming simulations performed and shown in the paper are valid for the balance fabric. The developed numerical model can be valid also for the no balance fabric, it will be tested and verified in the future work.

References

1. Bickerton S, Simacek P, Guglielmi SE, Advani SG. Investigaition of draping and its effects on the mold filling process during manufacturing of a compound curved composite part. Composites Part A. 1997; 28: 801-816.
2. Arbter R, Beraud JM, Binetruy C, Bizet L, Breard J, Demaria C, et al. Experimental Determination of the Permeability of Textiles: A Benchmark Exercise. Composites Part A . 2011; 42: 1157-1168.
3. Ouagne P, Bréard J. Continuous transverse permeability of fibrous media. Composites Part A. 2011; 41: 22-28.
4. Walther J, Simacek P, Advani SG. The effect of fabric and fiber tow shear on dual scale flow and fiber bundle saturation during liquid molding of textile composites. Int J Mater Form. 2012; 5: 83-97.
5. Bloom LD, Wang J, Potter KD. Damage progression and defect sensitivity: an experimental study of representative wrinkles in tension. Composites Part B. 2013; 45: 449-458.
6. Lee SH, Han JH, Kim SY, Youn JR, Song SY. Compression and Relaxation Behavior of Dry Fiber Preforms for Resin Transfer Molding. J Compos Mater. 2010; 44: 1801-1820.
7. Potter K, Khan B, Wisnom M, Bell T, Stevens J. Variability, fibre waviness and misalignment in the determination of the properties of composite materials and structures. Composites Part A. 2008; 39: 1343-1354.
8. Skordos AA, Aceves CM, Sutcliffe MPE. A simplified rate dependent model of forming and wrinkling of pre-impregnated woven composites. Composites Part A. 2007; 38: 1318-1330.
9. Allaoui S, Boisse P, Chatel S, Hamila N, Hivet G, Soulat D, et al. Experimental and numerical analyses of textile reinforcement forming of a tetrahedral shape. Composites Part A. 2011; 42: 612-622.
10. Khan MA, Mabrouke T, Vidal-Sallé E, Boisse P. Numerical and experimental analyses of woven composite renforcement forming using ahypoelastic behaviour. Application to the double dome benchmark. J Mater Process Technol. 2010; 210: 378-388.
11. Bel S, Hamila N, Boisse P, Dumont F. Finite element model for NCF composite reinforcement performing: Importance of inter-ply sliding. Composites Part A. 2012; 43: 2269-2277.
12. Peng X, Guo Z, Diu T, Yu WR. A simple anisotropic hyperelastic constitutive model for textile fabrics with application to forming simulation. Composites Part B. 2013; 52: 275-281.
13. Boisse P, Hamila N, Vidal-Sallé E, Dumont F. Simulation of wrinkling during textile composite reinforcement forming. Influence of tensile, in-plane shear and bending stiffnesses. Compos Sci Technol. 2011; 71: 683-692.
14. ten Thije RHW, Akkerman R. A multi-layer triangular membrane finite element for the forming simulation of laminated composites. Composites Part A. 2009; 40: 739-753.
15. Samir J, Echaabi J, Hattabi M. Numerical algorithm and adaptive meshing for simulation the effect of variation thickness in resin transfer molding process. Composites Part B. 2011; 42: 1015-1028.
16. Wang P, Legrand X, Boisse P, Hamila N, Soulat D. Experimental and numerical analyses of manufacturing process of a composite square box part: Comparison between textile reinforcement forming and surface 3D weaving. Composites Part B: Engineering. 2015; 78: 26-34.
17. Gatouillat S, Bareggi A, Vidal-Sallé E, Boisse P. Meso modelling for composite preform shaping – Simulation of the loss of cohesion of the woven fibre network. Composites Part A. 2013; 54: 135-144.
18. Liang B, Hamila N, Peillon M, Boisse P. Analysis of thermoplastic prepreg bending stiffness during manufacturing and of its influence on wrinkling simulations. Composites Part A. 2014; 67: 111-122.
19. Vanclooster K, Lomov SV, Verpoest I. Simulation of multi-layered composites forming. Int J Mater Form. 2010; 3: 695-698.
20. K. Vanclooster, Goidsenhoven SV, Lomov SV, Verpoest I. Optimizing the deep drawing of multilayered woven fabric composites. In 12th ESAFORM Conference on Material Forming. 2009; 2: 153-156.
21. K. Vanclooster, Lomov SV, Verpoest I. On the formability of multi-layered fabric composites. In 17th International Conference on Composite Materials. 2009.
22. Chen S, Endruweit A, Harper LT, Warrior NA. Forming simulations of multi-layered woven preforms assembled with stitch yarns. 16th European conference on composite materials. 2014.
23. Hamila N, Boisse P. Simulations of textile composite reinforcement draping using a new semi-discrete three node finite element. Composites Part B. 2008; 39: 999-910.
24. Carpenter Nicholas J, Taylor Robert L, Katona Michael G. Lagrange constraints for transient finite element surface contact. International journal for numerical methods in engineering. 1991; 32: 103-128.
25. Ben Boubaker B, Haussy B, Ganghoffer JF. Discrete models of woven structures. Macroscopic approach, Compos Part B. 2007; 38: 498-505.
26. Creech G, Pickett AK. Meso-modelling of Non-Crimp Fabric composites for coupled drape and failure analysis. Journal of Materials Science. 2006; 41: 6725-6736.
27. Durville D. Simulation of the mechanical behaviour of woven fabrics at the scale of fibers. Int J Mater Form 2010; 3: 1241-1251.
28. Rogers TG. Rheological characterisation of anisotropic materials. Composites. 1989; 20: 21-27.
29. Spencer AJM. Theory of fabric-reinforced viscous fluids. Compos Part A. 2000; 31: 1311-1321.
30. Yu WR, Pourboghrata F, Chungb K, Zampaloni M, Kang TJ. Non-orthogonal constitutive equation for woven fabric reinforced thermoplastic composites. Compos Part A. 2002; 33: 1095-1105.
31. Boisse P, Gasser A, Hagège B, Billoet JL. Analysis of the mechanical behavior of woven fibrous material using virtual tests at the unit cell level. J Mater Sci. 2005; 40: 5955-5962.
32. Peng X, Cao J. A continuum mechanics-based non orthogonal constitutive model for woven composite fabrics. Compos Part A. 2005; 36: 859-874.
33. Buet-Gautier K, Boisse P. Experimental analysis and modeling of biaxial mechanical behavior of woven composite reinforcements. Exp Mech. 2001; 41: 260-269.
34. Carvelli V, Corazza C, Poggi C. Mechanical modelling of monofilament technical textiles. Comput Mater Sci. 2008; 42: 679-691.
35. Willems A, Lomov SV, Verpoest I, Vandepitte D. Optical strain fields in shear and tensile testing of textile reinforcements. Compos Sci Technol 2008; 68: 807-819.
36. Prodromou AG, Chen J. On the relationship between shear angle and wrinkling of textile composite performs. Compos Part A. 1997; 28: 491-503.
37. Potter K. Bias extension measurements on cross-plied unidirectional prepreg. Compos Part A. 2002; 33: 63-73.
38. Peng XQ, Cao J, Chen J, Xue P, Lussier DS, Liu L. Experimental and numerical analysis on normalization of picture frame tests for composite materials. Compos Sci Technol. 2004; 64: 11-21.
39. Harrison P, Clifford MJ, Long AC. Shear characterisation of viscous woven textile composites: a comparison between picture frame and bias extension experiments. Compos Sci Technol. 2004; 64: 1453-1465.
40. Potluri P, Perez Ciurezu DA, Ramgulam RB. Measurement of meso-scale shear deformations for modelling textile composites. Compos Part A. 2006; 37: 303-314.
41. Lomov SV, Willems A, Verpoest I, Zhu Y, Barburski M, Stoilova Tz. Picture frame test of woven composite reinforcements with a full-field strain registration. Text Res J. 2006; 76 : 243-252.
42. Cao J, Akkerman R, Boisse P, Chen J, Cheng HS, de Graff EF, et al. Characterization of Mechanical Behavior of Woven Fabrics: Experimental Methods and Benchmark Results. Compos Part A. 2008; 39:1037-1053.
43. Wang P, Hamila N, Pineau P, Boisse P. Thermo-mechanical analysis of thermoplastic composite prepregs using bias-extension test. J Thermo Compos Mater. 2014; 27: 679-698.
44. Kawabata S. The Standardization and Analysis of Hand Evaluation. Osaka: The Textile Machinery Society of Japan. 1980.
45. Lahey TJ, Heppler GR. Mechanical Modeling of Fabrics in Bending. ASME J Appl Mech. 2004; 71: 32-40.
46. de Bilbao E, Soulat D, Hivet G, Gasser A. Experimental Study of Bending Behaviour of Reinforcements. Exp Mech. 2010; 50: 333-351.
47. Woven Composites Benchmark Forum.
48. J. Sargent, Chen J, Sherwood J, Cao J, Boisse P, Willem A, et al. Benchmark study of finite element models for simulating the thermostamping of woven-fabric reinforced composites. In 13th ESAFORM Conference on Material Forming. 2010; 3: 683-686.

Download PDF

Citation: Wang P, Hamila N and Boisse P. Numerical Studies about the Multi-Layered Textile Composite Reinforcement Forming. Adv Res Text Eng. 2016; 1(2): 1009. ISSN:2572-9373

Home

Journal Scope

Online First

Current Issue

Editorial Board

Instruction for Authors

Submit Your Article

Contact Us