
Review Article
Adv Res Text Eng. 2022; 7(2): 1073.
Equilibrium of Dyeing: A Review
Wolela AD*
Department of Textile Engineering, Wollo University; Kombolcha, Ethiopia
*Corresponding author: Asaye Dessie Wolela, Department of Textile Engineering, Kombolcha Institute of Technology, Wollo University; Kombolcha, Ethiopia
Received: June 30, 2022; Accepted: August 04, 2022; Published: August 11, 2022
Abstract
This paper presents equilibrium dyeing which is important in the dyeing process. The paper gives more emphasis on the dyeing equilibrium which is the position of sorption versus desorption after infinite time. In dyeing process, the investigation of the equilibrium dye distribution between the dye bath and the substrate is very important. The thermodynamics of dyeing of different textile fibers with their respective dyes type were discussed. Furthermore the three major types of dyeing adsorption isotherms, which are Nernst, Langmuir and Freundlich and the various dye/fibre systems correspond to one of these types. The most important thermodynamic parameters such as affinity, heat of dyeing and entropy of change which is determined at equilibrium have been also discussed. These values are useful in interpreting the driving force for dyeing processes and therefore provide a means for understanding what causes dye to transfer preferentially from the dye liquor into the fibre.
Keywords: Dye adsorption; Equilibrium dyeing; Adsorption isotherm; Thermodynamic parameters; Dye/Fiber system; Sorption; Desorption
Introduction
Chemical thermodynamics examines the energy-chemical reaction relationship and is applied to a system in equilibrium. It is more concerned with the final state than with the speed with which it is reached [1]. The analysis of the equilibrium dye dispersion between the dye bath and the substrate is particularly significant for a semiquantitative evaluation of a dyeing process [2]. When the system is at equilibrium, an adsorption isotherm relates the concentration of a substrate adsorbed on a solid surface (Df) to its concentration in the surrounding fluid (Ds) [3]. Isotherms involving adsorption can be associated with a particular sorption mechanism.
Chemical thermodynamics, according to examines the relationship between energy and chemical reactions and applies to a system in equilibrium, which is reached when a system’s macroscopic variables, such as temperature, pH value, dye concentration in the bath, dye amount on the fibre, and so on, do not change with time.
In the investigation of dyeing equilibria, heated the fibre and dye solution at a steady temperature until a state of equilibrium was obtained. The degree of exhaustion gradually becomes constant after the initial increase, but genuine equilibrium requires that the dye be uniformly dispersed throughout the fibres [3].
Studies of dyeing procedures in which the dyes disseminated into the fibre and the dye remaining in solution have attained equilibrium. This component includes the use of thermodynamic concepts and dyeing over far longer periods of time than are commercially possible. Also, He described that when a dyeing has reached equilibrium, dye is continually leaving the fibre and going back into the dye liquor, whilst simultaneously dye is continually arriving at the fibre surface and being adsorbed [4].
Wardman RH described also that, when a dyeing has reached equilibrium, dye is continually leaving the fibre and going back into the dye liquor, whilst simultaneously dye is continually arriving at the fibre surface and being adsorbed.
The purpose of studying the thermodynamics of dye adsorption (i.e. dyeing systems at equilibrium) is to elucidate the mechanism by which dye adsorption occurs and, in addition, to provide a quantitative measure of the tendency of the dye to pass from the solution phase to the fibre phase. The thermodynamics of dyeing is not concerned with the rate at which dyeing occurs but, rather, considers the dyeing process only when it has reached equilibrium and is commonly depicted in terms of an equilibrium adsorption curve [5].
Dyeing equilibria describes the position of sorption versus desorption after infinite time. Most of the equilibrium properties of dyeing system depend on three quantities: affinity, heat of dyeing and entropy change [6].
The amount of dye absorbed by a textile fibre at equilibrium when there is variation in temperature allows thermodynamic and kinetic sorption quantities such as standard affinity, heat of dyeing, entropy of dyeing and activation energy of diffusion to be evaluated [7]. The standard affinity, ?μ0 is the transfer of one mole of dye from its standard state in solution to its standard state in the fibre. The heat-content change during the dyeing process is the ?H0, whereas the degree of disorder of the dye molecules during the dyeing process corresponds to the entropy change, ?S° [8,9]. The thermodynamic of dyeing are influenced by the structural features in both the dye and polymer [10,11].
Adsorption thermodynamic and kinetic studies of C. I. disperse dye 60 on PBO fiber Pretreated with Polyphosphoric Acid (PPA) were carried out under the conditions. The results showed that the equilibrium adsorption isotherm of the disperse dye on the pretreated PBO fiber was a Langmuir-Nernst mixed Model. The thermodynamic parameters were calculated by the equilibrium adsorption isotherm, such as standard affinity, enthalpy change and entropy change, which indicated that the adsorption of disperse dye on the pretreated PBO fiber was an exothermic process [12].
ElifSahin, studied the equilibrium sorption isotherms of 3 reactive dyes (C. I. Reactive Yellow 84, C. I. Reactive Red 141, C. I. Reactive Blue 160) and their binary mixtures adsorbed on pre-wetted wool fiber were investigated. The isotherms obtained are Langmuir type. The rate parameters of adsorption kinetics decrease with increasing dye concentration [13].
Montra Chairat studied the adsorption and kinetic study of lac dyeing on silk. The pseudo second-order kinetic model was indicated with the activation energy. It was suggested that the overall rate of lac dye adsorption is likely to be controlled by the chemical process [14].
Thermodynamics of Dyeing Studies
The thermodynamics of adsorption of laccaic acids on silk has been studied, but without pH control and the results indicated that the adsorption isotherm of silk dyeing with laccaic acids, from which the erythro-laccinhad been removed, was of the Langmuir type [14,15].
Otutu JO, investigated the thermodynamic and kinetic properties of disazo dyes on polyester fibre and polyamide (nylon) fibre. The disazo dyes showed high affinity values on the two substrates under study. However, the affinity values of the dyes were slightly higher on polyester fibre than onnylon 6 fibre. It was also found that the enthalpy of dyeing, and entropy of dyeing values were slightly higher on polyester fibre than on the nylon 6 fibre [7].
The dyeing kinetics and thermodynamic parameters of direct dye as an example of the used dyes were enhanced by chemical modification via improving the structural characteristics of cotton fabrics as a result of the quaternization process [16].
Hema M and Arivoli S studied the sorption of Congo red, Malachite green and Rhodamine B dyes onto acid activated carbon. The equilibrium data are fitted to the Langmuir and Freundlich is other equations [17].
Jihong Wu, studied the dyeing thermodynamics for PLA fibre dyed with the natural dye curcumin. Linear isotherms are obtained, suggesting that the mechanism of dyeing is similar to that of disperse dyes [18].
The adsorption of Remazol Brilliant Blue R (RBBR) dye on pinang frond based activated carbon (PF-AC) was investigated in a batch process. The adsorption equilibrium and kinetic were found to follow Freundlich isotherm models and pseudo-second-order kinetic model, respectively. Result from adsorption thermodynamic show that interaction for RBBR dye was found to be feasible, nonspontaneous, and endothermic. The results indicated that the PFAC is very effective for the RBBR adsorption from aqueous solution [19].
Elif Sahin, investigated the interpretation of sorption kinetics for mixtures of reactive dyes on wool. This study focused on the adsorption and sorption rate constants of reactive dyes and dye mixtures on wool. The Langmuir kinetic model was used in determining adsorption and desorption rate constants for the dyes C. I. Reactive Yellow 84, C. I. Reactive Red 141 and C. I. Reactive Blue 160 [13].
Guan Y, investigated the adsorption thermodynamics of disperse dye on poly (p-phenylene benzobisoxazole) fiber pretreated with polyphosphoric acid. The adsorption isotherm of disperse dye on pretreated PBO fiber was a mixed Langmuir-Nernst model. As the temperature increased, the adsorption isotherm gradually shifted to the Nernst model [12].
Hou X studied adsorption kinetic and khermodynamic studies of silk dyed with sodium copper chlorophyllin. In this study, silk was dyed into a bright green shade with a natural dye derivative, Sodium Copper Chlorophyllin (SCC). Addition of sodium chloride increased SCC adsorption at equilibrium qe, increased the diffusion coefficient D and decreased the half dyeing time t1/2 [20].
Another studies were made oncationic dyeing equilibria on polyacrylonitrile fibers. Variation of the equilibrium uptake of cationic dyes with pH has shown that sulfonic groups in polyacrylonitrile fibers behave as weak acids. Deviations of experimental results from a Langmuir-type relation derived for competition between different cations for a limited number of anionic sites could be explained by electrostatic repulsive interactions between the sites [21].
Adsorption Isotherm Studies
The adsorption isotherm used to show the adsorption molecules distribute between the solid phase and liquid phase at adsorption equilibrium state. The Langmuir and Freundlich isotherms are the most frequently employed models [19].
Adsorption is usually described through isotherms, that is, functions which connect the amount of adsorbate on the adsorbent, with its pressure (if gas) or concentration (if liquid) [22].
Hema and Arivoli, studied equilibrium constant and thermodynamic parameters for the adsorption of dyes onto carbon. The experimental data are analyzed according to the linear form of the Langmuir and Freundlich isotherms [17].
The Langmuir isotherm is represented by the following equation [17,19,22,23].
Ce/Qe = 1/Qmb + Ce /Qm (1)
Here Ce is the equilibrium concentration (mg/L), Qe is the amount adsorbed at equilibrium (mg/g) and Qm and b are Langmuir constants related to the adsorption efficiency and energy of adsorption, respectively. The linear plots of Ce/Qe versus. Ce suggest the applicability of the Langmuir isotherms. The values of Qm and b are determined from the slope and intercept of the plots.
Langmuir’s isotherm model is based on the theory that adsorption energy is constant and uptake occurs on homogeneous surface by monolayer sorption. When the surface is covered by a monolayer of adsorbate, the adsorption goes on localized sites with no interaction between adsorbate molecules and that maximum adsorption occurs [19,22]. The Langmuir isotherm is well suited to describe dye adsorption by certain textile fibers. The Langmuir model is valid for monolayer sorption onto a surface with a finite number of identical sites [22].
The Langmuir adsorption model is established on the following hypotheses:
1. Uniformly energetic adsorption sites
2. Monolayer coverage
3. No lateral interaction between adsorbed molecules
At equilibrium, saturation point is reached where no furfurther adsorption can occur. A basic a ssumption is that sorption takes place at specific homogeneous sites within the adsorbent. Once a dye molecule occupies a site, no further adsorption can take place at that site [24].
The Freundlich equation is also employed for the adsorption of Congo Red (CR), Malachite Green (MG) and Rhodamine B (RDB) dyes on the adsorbent [17].
The Freundlich isotherm is represented as [17,19,22,23]:
Log Qe = log Kf+ 1/n log Ce (2)
Here Qe is the amount of Congo Red (CR), Malachite Green (MG) and Rhodamine B (RDB) adsorbed (mg/g), Ce is the equilibrium concentration of dye in the solution (mg/L) and Kf and n are constants incorporating all factors affecting the adsorption capacity and intensity of adsorption, respectively. Linear plot of log Qe versus. log Ce shows that the adsorption of CR, MG and RDB dye follows also the Freundlich isotherm [17].
The intensity of adsorption is an indication for the bond energies between dye and the adsorbent and the possibility of a slight chemisorption rather than physisorption. The possibility of multilayer adsorption of dyes through the percolation process cannot be ruled out [17].
Freundlich model is an empirical expression that is the earliest known relationship describing the sorption equation. This isotherm that takes into account a heterogeneous surface and multilayer adsorption to the binding sites located on the surface of the sorbent [19]. The Freundlich model assumes a heterogeneous multilayer adsorption surface with sites that have different energies of adsorption which are not equally available. In the case of the Freundlich model (Equation 2) the dye is considered as being contained in an internal phase of volume V of the fiber [22].
The Freundlich isotherm endorses the heterogeneity of the surface and assumes that the adsorption occurs at sites with different energy of adsorption. The energy of adsorption varies as a function of surface coverage [24].
The Nernst adsorption isotherm is considered as a limit case of Freundlich and Langmuir adsorption isotherms [22].
[C]f = KP ×[C]s (3)
Nernst isotherm equation is a mathematical representation of the distribution law, which states that a dissolved substance, irrespective of its total amount, distributes itself between two layers or phases in a constant concentration ratio, at constant temperature; the ratio, equal to the constant [22].
The adsorption process of the disperse dye on the polyester can be regarded as a distribution between two immiscible solvents (water and fiber). The isotherm parameters of disperse dye on polyester [12].
[D]f = [D]N= KN[D]s (4)
Where [D]N is the disperse dye concentration on polyester fiber calculated based on the Nernst adsorption model (mg/g); KN is the partition coefficient of the Nernst adsorption model (L/g).
The linear Nernst isotherm indicates that the fiber behaves as a solvent for the dye. Disperse dyes on many synthetic fibers such as polyester follows this type of isotherm. The Freundlich isotherm appears similar to the Nernst isotherm except the addition of the exponent, N, which is an empirical constant between zero and one. It is based on the fact that in most dye-fiber systems the partition coefficient decreases with increasing surface coverage. The Langmuir isotherm assumes that the adsorption of dye takes place on specific sites in the fiber, of which the number is limited. The sorption speed is proportional to the number of unoccupied sites as well as the concentration of the molecules in contact with the solid phase [1,25]. This isotherm is often applies to acid dyeing of nylon and wool. Both Freundlich and Langmuir isotherms have been used to describe the adsorption of direct dyes on cellulose. Even though there is no specific dye site in cellulose for direct dyes, Langmuir isotherm still shows a higher correlation for direct dye adsorptions than Freundlich isotherm [26,27].
However, for cotton dyeing with reactive dyes, the situation is more complex since the exhaust phase (described by an isotherm) is followed by a reactive phase (not reversible and cannot be described by any isotherm). Without the addition of alkali, the chemical reaction between cellulose and dye can hardly happen. Thus, the adsorption of reactive dye on cotton with no alkali is similar to direct dyes and either Freundlich or Langmuir isotherm can be applied [25].
In the Gilbert - Rideal theory, the activity coefficients of ions sorbed into the wool phase are reduced due to specific binding with sites on the wool, that is, the formation of ion pairs. Wool dyeing generally occurs in the presence of an acid as well as the dye (the acid is usually applied in a preliminary step). Gilbert and Rideal proposed that dye uptake is an anion exchange process, in which the dye molecules displace smaller anions [28].
In Donnan theory, the dye was considered to partition between the external solution and an internal solution phase in the wool. The latter phase is believed to contain a high concentration of fixed ionic groups, and hence solute molecules have reduced activity coefficients in that phase due to Coulombic interactions [28].
Clark M, explained that, in the two-phase (solution and fibre) model the sorbed molecules are considered dissolved in the surface layer which lacks specific adsorption points, hence also the term ‘diffuse adsorption’. The Donnan model of diffuse adsorption has been widely used to describe the sorption of dyes on cellulosics [1].
Riza Atav, Derbyshire and Peters, proposed a unified interaction theory for all dye-fiber systems, postulating that the principal contribution to the standard affinity of the dyes, of all classical types, to all kinds of fibers arises from the nonpolar Van der Waals forces. They postulated that non-polar forces are mainly responsible for dyefiber attachment and that in aqueous solution they occur between hydrophobic surfaces [22].
Thermodynamic Parameters
Thermodynamic parameters provide information of inherent energetic changes associated with adsorption. The thermodynamic adsorption parameters to be characterized are standard enthalpy (ΔH0), standard free energy (ΔG0), and standard entropy (ΔS0) [19].
The standard affinity, enthalpy change and entropy change are usually employed to describe the dyeing ability of a given dyestuff on a fiber, which were obtained according to thermodynamic theory. In a specific dyeing system, these values depend on the properties of the dye and fiber involved when the temperature, pressure and the amount of other components remain constant. Because the adsorption isotherm types of the disperse dye on the untreated and the pretreated PBO fiber were Langmuir model and Langmuir- Nernst mixed model, respectively, the thermodynamic parameters of the former adsorption and the front part of the latter adsorption would change with the alteration of the values of [D]f and [D]s [12].
The standard affinity (Δμ0), is defined for thermodynamically reversible systems, such as cotton and direct dyes, as a measure of the tendency of the dye to move from its standard state in the dye solution to its standard state in the fibre [29].
The standard affinity is a measure of the tendency of the dye moving from its standard state in solution to its standard state in fiber. The larger the value of standard affinity is, the larger the adsorption tendency of a dye on fiber [12,30]. The standard affinity values of the dye on the polyester were similar with that on the pretreated PBO. This result showed that the disperse dye could adsorb on the pretreated PBO fiber as well as on the polyester, and proved that dyeing the pretreated PBO fiber with disperse dye was practicable [12].
The standard affinity -Δμ0 (kJ/mol) of the dye on fibers was calculated using Equation (5) [7,12].
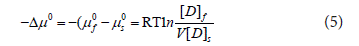
Where –μf0 is standard chemical potential of dye on the fiber; -μs0is standard chemical potential of dye in dyeing solution; R is universal gas constant (8.314 J/mol·K); T is absolute temperature (K); [D]f is dye concentration on the fiber (mg/g); [D]s is dye concentration of the adsorption solution (mg/L); V is effective volume of dyestuff on dry fiber in adsorption process.
Affinity (-Δμ°) is the most basic thermodynamic parameter of the dye in dyeing solution towards fiber substrate. The greater the degree of exhaustion at equilibrium the greater is the affinity [22,31].
The standard affinity for the distribution of dye between the fiber and dyebath isproportional to the logarithm of the ratio of the absolute activities of the dye in the fiber and dyebath. Since the activity of the dye is assumed to be directly related to its concentration, one can write equation as follows [22,32]:
Δμ° = RT [ In([C]F / [C]L)] (6)
Where Δμ°: standard affinity (J mol-1), R: gas constant (8.317 J K-1 mol-1), T: absolute temperature (°K), [C]F: concentration of dye on the fiber at equilibrium (g/l), [C]L: concentration of dye remaining in the dyebath at equilibrium (g/l).
The enthalpy change (ΔH0) manifested as heat of adsorption (kJ/ mol) in the adsorption process, which was calculated by Gibbs- Helmholtz equation Equation (7) [7,12,18].

Where -Δμ10 and -Δμ20 are the standard affinity at different temperatures respectively; T is absolute temperature (K).
The dyeing process is important in describing the heat of dyeing or the change in enthalpy of the system when adsorption takes place. As a result of dye molecules to be adsorbed on the fiber surface, free movement of these molecules gets restricted. So that entropy decreases when dye molecule is adsorbed. Adsorption also causes free energy to decrease [22].
The entropy change (ΔS0) of adsorption at different temperature (J/mol·K) was calculated using Equation (8) [7,12]
-Δμ 0 = TΔS0 - ΔH0 (8)
The change in entropy (ΔS0) represents the ratio of probability of sorption (β1) to that of desorption (β2) as shown in Equation (9) [22]:
ΔS0 = Rlnβ1 - Rlnβ2 = Rln(β1/β2) (9)
This entropy of sorption is the gain in entropy or disorder of the system when dye is adsorbed
Riza Atav described that, he change in entropy upon the sorption process consists of two parts, one of which results from the dehydration of dye molecules before their adsorption and the other is connected with the actual interaction of the molecules with the solid surface. While the latter part is negative (loss of the molecular freedom), the former is positive. During a spontaneous adsorption process, the total entropy change is always positive [22].
Hema and Arivoli studied equilibrium constant and thermodynamic parameters for the adsorption of dyes onto carbon. The thermodynamic parameters such as change in free energy (ΔG°) KJ/mol, enthalpy (ΔH°) KJ/mol and entropy (ΔS°) J/mol are determined using the following equations [17]:
K0= Csolid/Cliquid (10)
ΔG°=-RT lnKO (11)
IogK0 = ΔS°/ (2.303RT) - ΔH°/(2.303RT) (12)
Here Ko is the equilibrium constant, Csolid is the solid phase concentration at equilibrium (mg/ L), Cliquid is the liquid phase dye concentration at equilibrium (mg/L), T is the temperature in Kelvin and R is the universal gas constant. The values ΔH° and ΔS° obtained from the slope and intercept of Van’t Hoff plots.
In the case of physical adsorption, while increasing the temperature of the system, the extent of dye adsorption increases, this rules out the possibility of chemisorptions. However, the very low ΔH° value shows that the dye is physisorbed onto the adsorbent [33].
Hou X. et al. (2012) investigated adsorption kinetic and thermodynamic studies of silk dyed with Sodium Copper Chlorophyllin (SCC). The thermodynamic parameters of SCC adsorption with and without sodium chloride showed significant difference. The adsorption affinity (-Δμ°) and enthalpy change (ΔH°) of SCC dye on silk indicated that the adsorption is a spontaneous and exothermic process. SCC could be a good candidate as a natural green dye for protein fibers [20].
Conclusion
It can be concluded from this study that dyeing equilibrium studies the position of sorption versus desorption after infinite time. Most of the equilibrium properties of dyeing system depend on three quantities such as affinity, heat of dyeing and entropy change. The amount of dye absorbed by a textile fibre at equilibrium when there is variation in temperature allows thermodynamic and kinetic sorption quantities such as standard affinity, heat of dyeing, entropy of dyeing and activation energy of diffusion to be evaluated. The standard affinity, Δμ0 is the transfer of one mole of dye from its standard state in solution to its standard state in the fibre. The heat-content change during the dyeing process is the ΔH0, whereas the degree of disorder of the dye molecules during the dyeing process corresponds to the entropy change, ΔS°.
The equilibrium adsorption isotherm is fundamental in describing the interaction behaviour between solutes and adsorbents, and is important in the design of an adsorption system. The most commonly encountered adsorption isotherms in dyeing are Nernst, Langmuir and Freundlich isotherm. Most dyeing systems involving only adsorption are completely reversible. Equilibrium isotherms, established by adsorption of dye from solution onto initially undyedfibres, are identical to those obtained by desorption of dye from dyed fibres into an initially blank dyebath.
In addition to this, the paper review presented also the thermodynamic studies (dyeing equilibrium and adsorption isotherm) of different class of dyes on a textile substrate. It was also observed that the various dye/fibre systems correspond to one of the adsorption isotherm types.
Conflicts of Interest
The author declares no conflict of interest.
Funding
The authors do not receive any grant or financial support from any organization or supporting bodies.
References
- Clark M. Handbook of textile and industrial dyeing volume 1: Pprinciples, processes and types of dyes. Woodhead Publishing Series in Textiles; 2011.
- Zollinger H. Color chemistry: syntheses, properties, and applications of organic dyes and pigments. John Wiley & Sons; 2003.
- Broadbent AD. Basic principles of textile coloration. Bradford, UK: Society of Dyers and Colorists. 2001; 132.
- Wardman RH. An introduction to textile coloration: principles and practice. John Wiley & Sons; 2017.
- Burkinshaw SM. Physico-chemical aspects of textile coloration. John Wiley & Sons; 2016.
- Arora A, Gupta D, Rastogi D, Gulrajani ML. Kinetics and thermodynamics of dye extracted from Arnebianobilis Rech. f. on wool. Indian Journal of Fibre and Textile Research. 2012; 37: 178-182.
- Otutu JO, Ameuru US. Thermodynamic sorption parameters and kinetics of dyeing disazo dyes derived from 4-aminobenzoic acid and 4-amino-3- nitrotoluene on polyester fibre and polyamide fibre. Br J Appl Sci Technol. 2014; 4: 2955-69.
- Otutu JO. Synthesis and application of disperse dye derivatives of 4-aminobenzoic acid and 4-amino-3-nitrotoluene on synthetic polymer fibres. Int J Chem. 2010; 20: 147-55.
- OTUTU JO. Thermodynamic Absorption Parameters of Disazo Dyes derived from P-aminophenol and 4-aminobenzoic acid on Polyester Fibre and Nylon 6 Fibre. Mat Sci Res India. 2012; 9: 61-7.
- Kim TK, Son YA, Lim YJ. Thermodynamic analysis of 1, 4-diaminoanthraquinone adsorption on polyethylene terephthalate in alkane media. Dyes Pigments. 2007; 72: 246-50.
- Ujhelyiova A, Bolhova E, Oravkinova J, Tino R, Marcincin A. Kinetics of dyeing process of blend polypropylene/polyester fibres with disperse dye. Dyes Pigments. 2007; 72: 212-6.
- Guan Y, Mao YH, Wei D, Wang XX, Zhu PX. Adsorption thermodynamics and kinetics of disperse dye on poly (p-phenylenebenzobisoxazole) fiber pretreated with polyphosphoric acid. Korean J Chem Eng. 2013; 30: 1810-8.
- SAHIN E. Interpretation of sorption kinetics for mixtures of reactive dyes on wool. Turk J Chem. 2005; 29: 617-25.
- Chairat M, Rattanaphani S, Bremner JB, Rattanaphani V. An adsorption and kinetic study of lac dyeing on silk. Dyes Pigments. 2005; 64: 231-41.
- Kongkachuichay P, Shitangkoon A, Chinwongamorn N. Thermodynamics of adsorption of laccaic acid on silk. Dyes Pigments. 2002; 53: 179-85.
- Ibrahim SF, Michael MN, Tera FM. Characterization of dyeability and diffusion kinetics of chemically modified cotton fabrics towards disperse and direct dyes. Int J Adv Res Chem Sci. 2016; 3: 7-16.
- Hema M, Arivoli S. Comparative study on the adsorption kinetics and thermodynamics of dyes onto acid activated low cost carbon. Int J Phys Sci. 2007; 2: 10-7.
- Wu J, Guo H, Ke J, Fan J. Studies on kinetic and thermodynamic parameters of natural dye curcumin on PLA fibre. Indian Journal of Fibre and Textile Research. 2013; 38: 424-426.
- Ahmad MA, Herawan SG, Yusof AA. Equilibrium, kinetics, and thermodynamics of Remazol brilliant blue R dye adsorption onto activated carbon prepared from pinang frond. Int Sch Res Not. 2014; 2014.
- Hou X, Yang R, Xu H, Yang Y. Adsorption kinetic and thermodynamic studies of silk dyed with sodium copper chlorophyllin. Ind Eng Chem Res. 2012; 51: 8341-7.
- Rosenbaum S. Cationic dyeing equilibria on polyacrylonitrile fibers. Text Res J. 1963; 33: 899-910.
- Atav R. Thermodynamics of wool dyeing. Thermodynamics Fundamentals and Its Application in Science. 2012.
- Chairat M, Rattanaphani S, Bremner JB, Rattanaphani V. An adsorption and kinetic study of lac dyeing on silk. Dyes Pigments. 2005; 64: 231-41.
- Elmoubarki R, Mahjoubi FZ, Tounsadi H, Moustadraf J, Abdennouri M, Zouhri A et al. Adsorption of textile dyes on raw and decanted Moroccan clays: kinetics, equilibrium and thermodynamics. Water Resour Ind. 2015; 9: 16-29.
- Fu S. Studies on dyeing cationized cotton. North Carolina State University. 2016.
- Bairathi A. Dyeing sorption isotherms of three direct dyes and their mixtures on purified cotton. Text Chem Colorist. 1993; 25.
- Porter J J Interpretation of Sorption Isotherms for Mixtures of Direct Dyes on Cellulose. Textile Chemist & Colorist. 1993; 25.
- Bruce R L, Broadwood N V, King D G. Kinetics of wool dyeing with acid dyes. Textile Research Journal. 2000; 70: 525-531.
- Burdett BC. Physical chemistry essential to dyeing theory. The Theor Color Text. 1989; 1-96.
- Vickerstaff T. Physical chemistry of dyeing. 1950.
- Adebayo GB, Adekola FA, Olatunji GA, Bello IA. Some thermodynamic parameters of two indigenous mineral dyes applied on wool material. Bull Pure Appl Sci Chem. 2010; 29: 77-95.
- Lewis D M. Wool dyeing. Society of Dyers and Colourists. ED. 1992.
- McKay G, Poots VJP. Kinetics and diffusion processes in colour removal from effluent using wood as an adsorbent. J Chem Technol Biotechnol. 1980; 30: 279-92.