Intraglottal Flow Behavior in a CT-Based Laryngeal Model

Review Article

Austin J Otolaryngol. 2014;1(4): 7.

Intraglottal Flow Behavior in a CT-Based Laryngeal Model

Xue Q1*, Zheng X1 and Ye A2

1Department of Mechanical Engineering, University of Maine, USA

2Bangor High School STEM Program, Bangor High School, USA

*Corresponding author: Xue Q, Department of Mechanical Engineering, University of Maine, 5711 Boardman Hall, Room 219, Orono, ME, USA

Received: August 02, 2014; Accepted: October 25, 2014; Published: November 10, 2014

Abstract

A direct numerical simulation of flow-structure interaction was carried out in a subject-specific larynx model to study human phonation under physiological conditions. The effect of the realistic shape of the vocal fold and airway lumen on intraglottal flow dynamics was explored. It was found that the complex shape of the larynx, especially the lateral confinement of the airway lumen in the supraglottal region and the anterior-posterior asymmetry of the laryngeal shape, has a profound effect on intraglottal flow dynamics. Several important new findings that have not been captured in past simplified models were reported.

Keywords: Phonation; Vocal fold; Flow-structure interaction; Realistic laryngeal model; Intraglottal flow

Introduction

From a biomechanical point of view, voice production is intrinsically a multiphysics biological process resulting from complex nonlinear biomechanical interactions between glottal aerodynamics and vocal fold vibrations. The intraglottal region, which is also called the glottis, refers to the space/channel formed by the medial surface of the vocal folds. This is the region where the complex flow-structure interaction takes place and the primary sound sources are located. Considerable efforts have been undertaken to identify intraglottal flow behaviors and to ascertain their influence on the energy exchange during flow-structure interactions. Traditionally the intraglottal pressure was considered to be mainly governed by the Bernoulli’s effects [1-4]. The glottal flow was assumed to separate from the exit of the glottis and viscous loss was modeled as an empirical term obtained from the experimental data. Recently, more comprehensive experimental and numerical studies uncovered some more complex intraglottal flow behaviors and their important impacts on phonation [5-8]. During the glottal opening phase, a convergent shape of glottis is formed. Flow remains attached to the vocal fold wall within the glottis. A thin viscous boundary layer is developed and the intraglottal flow is mainly dominated by the Bernoulli’s effects. During the glottal closing phase, an adverse pressure gradient is induced by the divergent glottal shape and the boundary layer starts to separate from the vocal fold walls. Due to the inherent flow instability, the flow separation is asymmetric and the flow attaches to one side of the vocal fold walls until the glottal exit. The viscous “blockage effect” due to the boundary layer increases the flow impedance and alters the flow-pressure relationship [9]. Flow separation usually induces negative pressure (relative to the ambient pressure) around the superior portion of the divergent glottis [10]. This negative pressure determines the closing speed of the vocal fold, which has important implications for flow decline rate and vocal intensity [11-15]. Flow separation was also found to be a primary factor determining the phonation threshold pressure [16,17]. Furthermore, these viscous flow features, such as flow asymmetries, flow separations and vortical structure evolution, are highly unstable and constantly changing during a phonatory cycle. For instance, dynamic flow separation has been widely observed [18-20]. A recent experimental investigation showed that the development of intraglottal flow asymmetries is dependent on the acceleration of flow [7]. A more recent study observed that flow asymmetries in the dynamic models appear later in the cycle than in the static models [21].

While the aforementioned studies greatly improve the understanding of intraglottal flow behaviors, they were all conducted by using static and/or simplified larynx models. Therefore, their validity remains to be assessed by using a dynamic realistic laryngeal model. The larynx has a complex anatomical structure and the unsteady viscous flow is very sensitive to the geometry of larynx. For instance, intraglottal vorticity-velocity interaction, glottal jet structure and its transition to turbulence were all demonstrated to be highly three-dimensional [22,23,20]. The sub and supraglottal lumen in the human larynx has significant variations in the anterior-posterior direction which affects those flow behaviors [24]. Flow-induced vibration of vocal folds was also observed having strong anterior-posterior variations in high speed imaging studies [25].

In our previous study, we have successfully conducted a flow-structure interaction simulation in a subject-specific larynx model [24]. The obtained flow parameters and vibration pattern were found to be within the normal phonation range. The current study will extend this earlier study by comprehensively examining the intraglottal flow behaviors with the aim to provide additional insights into intraglottal flow dynamics under realistic physiological conditions.

Computational Model

The numerical algorithm and simulation set up have been reported in details in our previous study [24]. For the sake of completeness, the current paper describes concisely some salient features of the numerical methods, geometric model, contact model, boundary conditions, and material properties. The current study employed an explicitly coupled immersed-boundary-finite-element method based flow-structure interaction solver to model human phonation. Glottal airflow was governed by the 3D, unsteady, viscous, incompressible Navier-Stokes equations, and vocal fold dynamics was governed by the Navier equation. The coupling between the flow and solid solvers was implemented by tracking the aerodynamic load on the interface mesh as well as its deformed shape and velocity in a Lagrangian fashion.

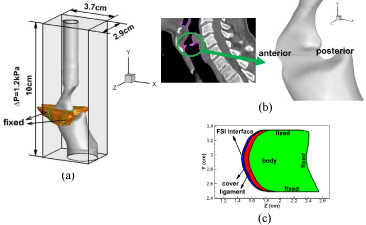
The geometry of the airway lumen and vocal fold was reconstructed based on a CT scan of the larynx of a 30-year-old male subject by using the commercial medical image processing software, Mimics. It should be pointed out that the vibration part of the vocal fold was very blurry in the CT image. Therefore we manually adjusted the segmented model so that medial surface of the vocal fold aligns with the centerline of the glottis. Figure 1 (a) & (b) show the three-dimensional geometry of the airway lumen and vocal folds. The approximate dimension of each vocal fold was 0.9cm (thickness) × 1.0cm (depth) × 1.4 cm (length). Two artificial straight tubes were connected to both the subglottal trachea and the supraglottal pharynx to provide sufficient distance to apply uniform pressure boundary conditions. The model of the airway lumen and vocal folds were immersed into a 10cm (inferior-superior) × 2.9cm (medial-lateral) × 3.7cm (anterior-posterior) rectangular box, as shown in Figure 1(a). The vocal folds were located between the planes of y=2.5cm and y=3.5cm. Zero and 1.2kPa gauge pressure are applied at the outlet and inlet, respectively, yielding a typical 1.2kPa pressure drop across the vocal tract. Non-slip-non-penetration flow condition was applied on all of the lumen walls. To deal with the contact between two vocal folds during closed phase, we applied a kinematic constraint on the vocal folds to enforce a minimum glottal gap of 0.01 cm. This minimum gap is necessary for the success of the flow solver, but it also allows some “leakage” flow even when the vocal folds are considered completely closed.

Figure 1 :(a) Computational domain and laryngeal model. The solid lines on the vocal folds indicate the position beyond which the two ends of the vocal fold are fixed. (b) A high resolution CT scan image of human larynx and the geometric model of the laryngeal airway (c) The inner layer structure and boundary conditions of the vocal fold model.






Figure 1 : (a) Computational domain and laryngeal model. The solid lines on the vocal folds indicate the position beyond which the two ends of the vocal fold are fixed. (b) A high resolution CT scan image of human larynx and the geometric model of the laryngeal airway (c) The inner layer structure and boundary conditions of the vocal fold model.

Due to the same tissue density, the internal structure of the vocal fold cannot be segmented from the CT image. We empirically employed the typical three-layer structure for the current model, which consisted of the cover, ligament and muscle layers. The configuration of the internal structure of the vocal fold is also shown in Figure 1(c). The thickness of the cover layer and ligament layer were taken from the histological measurement, which were 0.03 cm and 0.1 cm, respectively, and it was assumed to be constant along the anterior-posterior direction. The material of the three layers was assumed to be linear, viscoelastic, and transversally isotropic. The material properties for each layer are reported in Table 1. It should be noted that vocal folds barely vibrate in the longitudinal direction during phonation, and therefore, an in-plane motion constraint was implemented by setting the longitudinal Young’s modulus equal to 104 times the transversal Young’s modulus in each layer. A zero displacement boundary condition was imposed on the lateral, inferior and superior surfaces of the vocal fold and a traction boundary condition was applied on the portion of the medial surface of the vocal fold which overlaps with the lumen surface. The anterior and posterior ends of the vocal fold were anchored on the arytenoid and thyroid cartilages. The portions of the vocal fold beyond the anchors were fixed, as shown in Figure 1(a). Each vocal fold was discretized with a dense mesh consisting of 23973 tetrahedral elements.

Table 1: Material properties of the three-layers of the vocal fold. ρ is the tissue density, Ep is the transversal Young’s Modulus, Vp is the in-plane transversal Poisson’s ratio, Epz is the longitudinal Young’s Modulus, Vpz is the longitudinal Poisson’s ratio and Gpz is the longitudinal shear modulus.




  

    
Layer

    
Property

  

  

    
ρ(g/cm3) 

    
Ep(kPa) 

    
Vp 

    
Epz(kPa) 

    
Vpz 

    
Gpz(kPa)

      
 

    
η(poise) 

  

  

    
Cover

    
1.043

    
1.00

    
0.9

    
10000

    
0.0

    
10

    
1

  

  

    
Ligament

    
1.043

    
1.15

    
0.9

    
11500

    
0.0

    
20

    
1

  

  

    
Body

    
1.043

    
2.00

    
0.9

    
20000

    
0.0

    
12

    
1

  









Table 1:  Material properties of the three-layers of the vocal fold. ρ is the tissue density, Ep is the transversal Young’s Modulus, Vp is the in-plane transversal Poisson’s ratio, Epz is the longitudinal Young’s Modulus, Vpz is the longitudinal Poisson’s ratio and Gpz is the longitudinal shear modulus.

The flow solver employed a high resolution, non-uniform 64×256×128 Cartesian grid for the computational domain. The highest grid density was provided around the intraglottal and near-supraglottal regions. The minimum glottal gap width was resolved to at least two points in the Z direction. A small time step of 3.5×10- 3ms was employed for both the flow solver and the solid dynamics solver to provide good temporal resolution as well as to satisfy the CFL stability constraint. The simulation was carried out on a 6.1 Tera FLOPS cluster from Penguin Computing with 512 compute cores running at 3.0 Ghz, with 3 TB of RAM and 40 Gbps QDR Infiniband for interprocess communication. The wall clock time was 240 h and the overall computational expense was 30,720 CPU hours.

Results and Discussion

Glottal exit velocity and pressure relationship

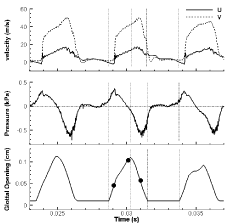
Figure 2 shows the waveforms of the glottal exit velocity, glottal exit pressure and glottal opening size over three successive cycles at the plane of x=0.9cm, which is near the mid-coronal plane of the glottis. The glottal opening size is defined as the minimum distance between the two vocal folds at the plane. The fundamental frequency was calculated based on the waveform of the glottal opening size. It is 195Hz, relatively high for a male subject. This is most likely due to the large value of the longitudinal Young’s modulus employed in the vocal fold model. The open quotient and skewing quotient were also calculated from the waveform of the glottal opening size. The open quotient is defined as the ratio of the time duration in each cycle when the glottis is open to the period of the cycle, and the skewing quotient is defined as the ratio of the time duration in each cycle when the glottis is opening to the time duration during which the glottis is closing. The physiological range for the open quotient and skewing quotient is 0.4-0.7 and 1.1-3.4, respectively [26]. In the current simulation, they are 0.6 and 1.28, respectively, indicating that a typical glottal waveform for normal phonation was successfully captured.

Figure 2 :Time-variation of the glottal exit velocity, glottal exit pressure and glottal opening size at the plane of x=0.9 cm over three successive cycles.






Figure 2 : Time-variation of the glottal exit velocity, glottal exit pressure and glottal opening size at the plane of x=0.9 cm over three successive cycles.

As previously mentioned, most of past studies relied on simplified laryngeal models in which the airway lumen was straight and the glottis was either rectangular or symmetrically lens-shaped. With such simplified shapes, especially rectangular glottis, the intraglottal flow was usually assumed to be two-dimensional, with the anterior-posterior velocity component being ignored. Recently, this flow simplification was criticized by Scherer et al. [27] who pointed out that the anterior-posterior velocity could become significant in a lens-shaped glottis due to the variation of the opening size along this direction. They measured the anterior-posterior velocity in a convergent 10O glottis with the lens shape, and reported that the magnitude of the anterior-posterior velocity was approximately 10% of the axial (superior-inferior) velocity. While this work is important by discovering the three-dimensionality of the intraglottal flow, its measurement was still based on a static straight flow channel. As shown in Figure 1(b), in the realistic larynx, the subglottal and supraglottal flow channels are not straight, but incline in opposite directions in the x-y plane with the turning point at the glottal neck. Such inclination would be expected to produce even stronger anterior-posterior velocities in realistic larynx. To illustrate this effect, Figure 2(a) shows the waveform of both anterior-posterior (U) and inferior-superior (V) velocities at the glottal exit at the plane of x=0.9cm. The glottal exit was assumed to align with the top surface of the vocal fold which is at the plane of y=3.5cm. It should be pointed out that the anterior-posterior velocity component at this plane was along the negative x direction due to the inclined direction of the subglottal tube. For the sake of comparison, negative anterior-posterior velocity is shown in Figure 2(a). The magnitude for anterior-posterior and inferior-superior velocities was about 17m/s and 50m/s, respectively. Therefore, the magnitude of the anterior-posterior velocity was about 1/3 of the inferior-superior velocity, much more significant than the observations from the previous simplified model [27]. It implies that the midcoronal plane is not sufficient to fully describe the features of the laryngeal flow. In addition, strong velocity toward the anterior commissure suggests a strong interaction between the laryngeal flow and anterior wall, which might contribute to additional sound source.

The gauge pressure at the glottal exit shown in Figure 2 is observed to be generally 180O out of phase from the glottal exit velocity; it decreased as the flow velocity increased and vice versa. The pressure was mostly positive during the glottal opening phase and negative during the closing phase. This phase-dependent pressure change plays an auxiliary role in the movements of the vocal folds, with the positive pressure pushing the vocal folds during the opening phase and the negative pressure pulling the vocal folds during the closing phase.

Intraglottal pressure distribution

It was extensively observed that, when the glottis presents a diverging shape, glottal jet flows out of the glottis not following the straight path, but completely attaching to one of the vocal folds and separating from the other side of the vocal fold walls [28-32,7,18]. This asymmetry in the flow field causes asymmetric aerodynamic pressure on vocal folds, and thus is believe to influence sound production. It was also reported that strong intraglottal vortices would be generated and stay near the flow separation point, which can induce low local pressure on the vocal folds [10] and can further increase pressure asymmetry between the two vocal folds. However, these observations were all made with simplified/static laryngeal models or excised vocal fold model with simplified vocal tract in which the glottal flow typically experienced sudden expansion from the intraglottal region to supraglottal region. If the flow asymmetry and pressure asymmetry would occur in the realistic glottis remains unexplored.

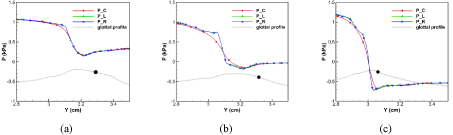
The intraglottal pressure distribution in the current realistic laryngeal model was investigated to answer the above question. Figure 3 plots the pressure on the two vocal fold walls along the vertical direction and along the centerline of the glottis at the plane of x=0.8cm at three different time instants within a phonation cycle. The four time instants are: t=0.02905s, 0.0301s and 0.0310s, respectively, which correspond to the moments of glottal opening, maximum glottal opening and glottal closing. The time instants have been marked as “.” in Figure 2 accordingly. In the subsequent sections, we will use (a)~(c) to refer these three instants. To illustrate the relationship between pressure distribution and glottal shape, the profile of one side of glottal surfaces at the same instant is also included in the plots. The “.” on vocal fold profiles indicates the location of the flow separation at that time instant.

Figure 3 :Intraglottal pressures on the two vocal fold walls along the vertical direction and along the centerline of the glottis at the plane of x=0.8cm at three time instants within a vibration cycle. The four time instants are (a) t= 0.02905s, (b) t=0.0301s and (c) t=0.0310s. P_C, P_L and P_R represent the pressure on the centerline, left vocal fold surface, and right vocal fold surface, respectively. The dotted line represents the profile of one of the vocal fold walls. The “.” Indicates the location of flow separation on the vocal fold wall.






Figure 3 : Intraglottal pressures on the two vocal fold walls along the vertical direction and along the centerline of the glottis at the plane of x=0.8cm at three time instants within a vibration cycle. The four time instants are (a) t= 0.02905s, (b) t=0.0301s and (c) t=0.0310s. P_C, P_L and P_R represent the pressure on the centerline, left vocal fold surface, and right vocal fold surface, respectively. The dotted line represents the profile of one of the vocal fold walls. The “.” Indicates the location of flow separation on the vocal fold wall.

It can be observed that the vocal fold surface pressure and glottis centerline pressure presented the same general pattern that they quickly decreased along the convergent portion of the glottis until the minimum glottal gap, and then gradually recovered along the divergent portion of the glottis. Figure 3 also confirms our observation in Figure 2 that during the glottal opening phase the intraglottal pressure remained positive facilitating the outward motion the vocal folds, and during the closing phase the intraglottal pressure remained mostly negative pulling the vocal fold back to the center.

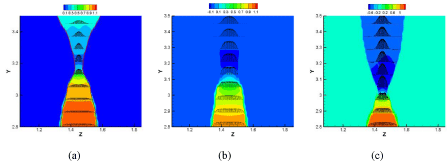
It is worth noting that the vocal fold surface pressure remained the same for both sides throughout the cycle, implying a symmetric flow field within the glottis. In order to clearly visualize the flow field, Figure 4 shows the contour of pressures inside the glottis at the plane of x=0.8cm at the three corresponding time instants. Velocity vectors were also overlaid to show the flow behavior. It can be observed that the pressure and velocity vectors were nearly symmetric about the centerline. The flow maintained a straight path along the centerline and separated symmetrically starting from the divergent portion of the glottis. The location of the separation was right after the minimum glottal gap. During the cycle, the separation point followed the location of the minimum glottal gap moving from downstream to upstream. The observed symmetric flow and pressure distribution in the current model contradicts to the previous observations of asymmetric glottal flow configuration in simplified models [28-32,7,18]. To explore the cause of the absence of the asymmetric glottal flow configuration in the current study, it is necessary to examine the potential factors which could cause symmetry breaking of a jet flow. The Reynolds number is important for jet instability and a decreased Reynolds could suppress the asymmetry of glottal jet. The Reynolds number in the current model is about the same as the one in the previous simplified model in which flow asymmetry was observed. Therefore, the effect of Reynolds can be excluded. Many studies suggested the “Coanda effect”, or the intraglottal instability, as the cause of the flow asymmetry [31,7,33]. They asserted that as the glottal jet moves forth, it tends to entrain the ambient fluid to move together. This entrainment causes the acceleration and pressure drop in the region between the jet and wall. As the imbalanced pressure drops on both sides arising from the viscous instability, the jet is eventually pulled toward one of the walls. The divergent angle of the glottis is critical to the establishment of intraglottal instability. It was reported that intraglottal instability would occur when the divergent angle is larger than 10O [7]. In the current configuration at the plane of x=0.8cm, the divergent angle of the glottis can reach up to 40O; however, flow asymmetry was not observed. It suggests that intraglottal instability may not be the primary factor responsible for glottal flow asymmetry. Recently, several other studies proposed that glottal flow asymmetry may be induced by the vortex dynamics downstream of the vocal folds [34-37]. In their studies, the breaking of flow symmetry was found to start from the supraglottal region and propagate upstream into the glottis. In addition, the flow deflection direction was well correspondence with the supraglottal vortex structures near the glottal exit which entrained the glottal jet as it emanated from the glottis. This breaking of flow symmetry is because of the supraglottal instability arising from the sudden expansion from the glottis to the supraglottal region in these simplified models. In the current realistic shape model, the airway lumen is gradually expanded from the glottis to the supraglottal region. The gradual expansion exerted a stronger lateral confinement on the glottal jet which greatly stabilized the jet. The reduced supraglottal space also suppressed the development supraglottal vortices. Therefore, we hypothesize that glottal flow tends to remain straight in the realistic configuration and it is because of the strong lateral confinement in the supraglottal region which stabilizes the jet and suppresses the development of supraglottal vortices. Such feature has important implications for maintaining stable voice quality. First, it has been shown in the past that asymmetric flow would apply asymmetric aerodynamic pressure on the two vocal folds which may desynchronize the vibration of vocal folds. The real shape of the larynx suppresses the asymmetry of the flow and consequently diminishes this desynchronization effect. Second, the stable jet in the real shape will also lead to stable sound sources. The asymmetric flow obtained in the simplified model with sudden expansion has been shown to vary in deflection angle and deflection direction from cycle to cycle. This results in great variability of the flow field from cycle to cycle, especially in the supraglottal region where vortical structures are important for dipole source and quadruple source generation. With a more stable jet in real shape larynx, flow variability will be reduced significantly. A more stable flow filed will result in a more stable sound source field which is important for stable sound quality. Third, the strong confinement effect of the supraglottal wall will also reduce the flow instability induced by the asymmetric vocal fold vibration which typically occurs in patients with unilateral laryngeal paralysis. Even though the asymmetric vocal fold vibration could induce the asymmetric flow through the vocal folds in this case, the confinement of the supraglottal wall will stabilize this jet in the supraglottal region, making the sound source field stable which compensates the effect of asymmetric vibrations.

Figure 4 :The contour of intraglottal pressures and the vectors of the vertical velocity at the plane of x=0.8 cm at four time instants corresponding to Figure 3. The four time instants are (a) t= 0.02905s, (b) t=0.0301s and (c) t=0.0310s.






Figure 4 : The contour of intraglottal pressures and the vectors of the vertical velocity at the plane of x=0.8 cm at four time instants corresponding to Figure 3. The four time instants are (a) t= 0.02905s, (b) t=0.0301s and (c) t=0.0310s.

Figure 3 also shows the difference between the vocal fold surface pressure and glottal centerline pressure which exits in the convergent portion of the glottis up to the separation point. The non-uniform cross-channel pressure distribution is more obvious at the time instants (b) and (c) when the flow velocity is high. It can be observed in Figure 4 that the pressure contours in the convergent portion were curved with a concave shape, meaning that the pressure was lowest at the centerline and higher close to the wall. The curved pressure contours were caused by the curved streamlines which aligned with the shape of the glottis in the convergent portion. After the flow passed the minimum glottal gap, the glottis started to expand. The streamlines started to curve in opposite directions, so did the pressure contours. Consequently, downstream to the minimum glottal gap, the centerline pressure became higher than the vocal fold surface pressure. The difference between the centerline pressure and vocal fold surface pressure disappeared after the flow separation point because the glottal jet maintained constant width after the flow separation point. The streamlines of the jet were almost straight, so the pressure was relatively uniform.

Anterior-posterior asymmetry in flow field

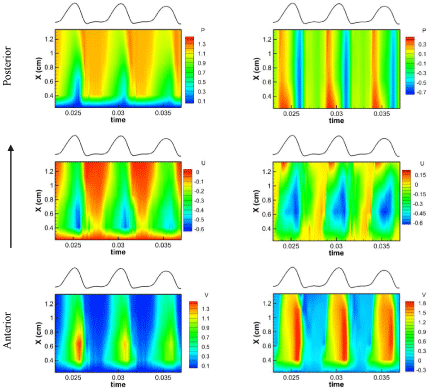
The shape of the realistic larynx shows significant variations along the anterior-posterior direction. To investigate the influence of the anterior-posterior variation of the geometry on the flow, the spatiotemporal plots of the pressure, anterior-posterior velocity (U) and inferior-superior velocity (V) along the anterior-posterior direction at two vertical locations on the mid-sagittal plane are shown in Figure 5. In the plots, the vertical axis is the anterior-posterior location and horizontal axis is the time. The two vertical locations are the planes of y=2.92cm and y=3.32cm, corresponding to subglottal and supraglottal regions, respectively. The minimum glottal gap moved between these two planes during vibrations. In the following context, these two planes are called subglottal plane and supraglottal plane, respectively. The volume flow rate is also included in each plot. Several interesting findings are observed regarding the pressure and velocity distributions along the anterior-posterior direction.

Figure 5 :Spatiotemporal plots of the pressure, anterior-posterior velocity and vertical velocity as a function of the anterior-posterior location and time at two vertical locations on the mid-sagittal plane. The two vertical locations are at y=2.92cm and y=3.32cm, corresponding to subglottal and supraglottal regions, respectively. The flow rate is also included in each plot.






Figure 5 : Spatiotemporal plots of the pressure, anterior-posterior velocity and vertical velocity as a function of the anterior-posterior location and time at two vertical locations on the mid-sagittal plane. The two vertical locations are at y=2.92cm and y=3.32cm, corresponding to subglottal and supraglottal regions, respectively. The flow rate is also included in each plot.

First, the amplitude of the pressure and velocities decreased from the anterior end to the posterior end at the subglottal plane, as shown in Figure 5 (a). It is mainly because of the subglottal angle variation along the anterior-posterior direction. It was reported in the previous study [24] that the subglottal angle in the current laryngeal model increased from the anterior to posterior aspects. To satisfy the continuity of the flow, the flow velocity at the anterior end was higher than the posterior end. The pressure was accordingly lower at the anterior end. It’s worth noting that such anterior-posterior asymmetry of amplitude in pressure and velocities was not observed on the supraglottal plane. As shown in Figure 5 (b), the pressure was mostly uniform along the anterior-posterior direction, and the velocity amplitude was highest at the mid-coronal plane and decreased toward both anterior and posterior ends. It is because the supraglottal angle is nearly uniform along the anterior-posterior direction.

Second, anterior-posterior phase difference of both pressure and velocities at the subglottal plane was observed at both the beginning and the end of cycles. It can be seen from Figure 5 (a) that for both pressure and velocities the anterior end leaded the posterior end at the beginning of the cycle and posterior end leaded the anterior end at the end of each cycle. This is mainly because of the asymmetric opening and closing of the glottis. It was found in the previous work that the glottis opening started from the anterior end and propagated to the posterior end [24]. Consequently, the velocities the subglottal plane increased earlier at the anterior end. Reversely, the glottal closure was found to occur first at the posterior end and last at the anterior end. Therefore, the velocity at the subglottal plane dropped to zero earlier at the posterior end. This asymmetric opening and closing of the glottis was the combined effect of the asymmetric subglottal pressure distribution and vertical motion of the vocal folds [24]. The phase difference in the velocity waveforms also causes phase difference in the pressure waveform at the subglottal plane. It should be noted that the anterior-posterior phase difference of the waveforms at the beginning and the closing of the cycles can also be seen on the velocity waveforms of the supraglottal plane, but with much smaller values. The anterior-posterior velocity (U) at the supraglottal plane also presented large phase difference in the middle of the cycle, with the center region leading the off-center regions. Phase difference was not observed in the waveform of the pressure on the supraglottal plane. These observations suggest that vocal fold dynamics has greater effect on the subglottal flow, but little effect on the supraglottal flow.

Third, a different pressure-velocity relationship was observed on the supraglottal plane at the beginning of cycles. It can be clearly seen from Figure 5 that, during each entire cycle on the subglottal plane and the later part of each cycle on the supraglottal plane, the pressure-velocity relationship was predominated by the Bernoulli’s principle that the pressure decreased as the velocity increased, and then increased as the velocity decreased, even though the total pressure is fluctuating within one cycle. However, at the beginning of each cycle on the supraglottal plane, a reverse relationship was observed that the pressure and velocity increased simultaneously. It is mainly due to the unsteady effect associated with the buildup of the glottal pressures. Assuming there is no leakage flow, for each cycle, before the glottis opened, the subglottal and supraglottal regions were separated. At this moment, the subglottal pressure was close to the applied pressure on the inlet (1.2kPa) and the supraglottal pressure was almost equal to 0. When the glottis just opened, flow passed through the glottis. The pressure needed to be built up in the supraglottal region. Therefore, a pressure increase was observed at the very beginning of cycles. After a short period, when the supraglottal pressure has been built, the relationship between the pressure and velocity became predominated by the Bernoulli’s principle again.

Conclusion

A direct numerical simulation of flow-structure interaction was carried out on a subject-specific larynx model to study human phonation under physiological conditions. The effect of the realistic shape of the vocal fold and airway lumen on intraglottal flow dynamics was explored in the current study. Several main findings are summarized below.

First, the three-dimensionality of the flow is significant in the realistic airway. It was found that the magnitude of the anterior-posterior velocity was about 1/3 of the inferior-superior velocity, and this secondary flow moved from the posterior end to the anterior end because of the inclined shape of the subglottal lumen. The flow rate is significantly affected due to the existence of this secondary flow compared to other simplified models.

Second, because of the strong lateral confinement and the gradual expansion of the supraglottal wall, the glottal flow was found to be nearly straight inside the glottis and the flow pressure were symmetric on both vocal fold walls. However, due to the curved streamlines in the subglottal and glottis region, the centerline pressure in these two portions appeared to be different from the vocal fold surface pressure.

Third, strong anterior-posterior asymmetry was found in the subglottal flows. The amplitude of the pressure and velocity waveforms decreased from the anterior end to the posterior end in the subglottal flow because of the variation of the subglottal angle in the anterior-posterior direction. Clear anterior-posterior phase difference of pressure and velocity waveforms was also observed in the subglottal flow with the anterior end leading the posterior end at the beginning of each cycle and posterior end leading the anterior end at the end of each cycle. This finding is consistent with the observation of the asymmetric opening and closing of the glottis.

Fourth, the pressure-velocity relationship in the glottis was predominated by the Bernoulli’s principle, regardless of the fluctuation of the total pressure. However, a significant pressure increase was observed for the supraglottal flow at the beginning of the cycle due to the buildup of the glottal pressure.

The above observations from a realistic laryngeal model reveal some previously unappreciated important flow behaviors. It suggests that results from the simplified models may be still useful in that they predict general behavior of the glottal flow; however, care would need to be taken when applying these results to realistic laryngeal shapes. In future studies, more realistic laryngeal models may be required to capture accurate data for studying laryngeal functions.

References

  1. Berg JVD, Zantema JT, Doornenbal PJ. On the air resistance and the Bernoulli effect of the human larynx. J. Acoust. Soc. Am. 1957; 29: 626-631.
  2. Ishizaka K, Flanagan JL. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Syst. Tech. J. 1972; 51: 1233–1268.
  3. Story BH, Titze IR. Voice simulation with a body-cover model of the vocal folds. J Acoust Soc Am. 1995; 97: 1249-1260.
  4. LaMar MD, Qi Y, Xin J. Modeling vocal fold motion with a hydrodynamic semicontinuum model. J Acoust Soc Am. 2003; 114: 455-464.
  5. Pelorson X, Hirschberg A, Hassel RR, Wijnands APJ. Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation. Application to a modified two-mass model. J. Acoust. Soc. Am. 1999; 96: 3416-3431.
  6. Scherer RC, Shinwari D, De Witt KJ, Zhang C, Kucinschi BR, Afjeh AA, et al. Intraglottal pressure distributions for a symmetric and oblique glottis with a uniform duct. J Acoust Soc Am. 2002; 112: 1253-1256.
  7. Erath BD, Plesniak MW. An investigation of bimodal jet trajectory in flow through scaled models of the human vocal tract. Exp. Fluids. 2006; 40: 683–696.
  8. Suh J, Frankel SH. Numerical simulation of turbulence transition and sound radiation for flow through a rigid glottal model. J Acoust Soc Am. 2007; 121: 3728-3739.
  9. Krane MH, Wei T. Theoretical assessment of unsteady aerodynamic effects in phonation. J Acoust Soc Am. 2006; 120: 1578-1588.
  10. Mihaescu M, Khosla SM, Murugappan S, Gutmark EJ. Unsteady laryngeal airflow simulations of the intra-glottal vortical structures. J Acoust Soc Am. 2010; 127: 435-444.
  11. Sundberg J, Gauffin J. Waveform and spectrum of the glottal voice source. Frontiers of Speech Communication Research. 1979.
  12. Holmberg EB, Hillman RE, Perkell JS. Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice. J Acoust Soc Am. 1988; 84: 511-529.
  13. Gauffin J, Sundberg J. Spectral correlates of glottal voice source waveform characteristics. J Speech Hear Res. 1989; 32: 556-565.
  14. Sapienza CM, Stathopoulos ET. Comparison of maximum flow declination rate: children versus adults. J Voice. 1994; 8: 240-247.
  15. Gorham-Rowan M, Morris R. Aerodynamic analysis of male-to-female transgender voice. J Voice. 2006; 20: 251-262.
  16. Lucero JC. Optimal glottal configuration for ease of phonation. J Voice. 1998; 12: 151-158.
  17. Zhang Y, Jiang JJ. Acoustic analyses of sustained and running voices from patients with laryngeal pathologies. J Voice. 2008; 22: 1-9.
  18. Hofmans GC, Groot G, Ranucci M, Graziani G, Hirschberg A. Unsteady flow through in-vitro models of the glottis. J Acoust Soc Am. 2003; 113: 1658-1675.
  19. Erath BD, Plesniak MW. A theoretical model of the pressure field arising from asymmetric intraglottal flows applied to a two-mass model of the vocal folds. J. Acoust. Soc. Am. 2011a; 130: 389-403.
  20. Zheng X, Mittal R, Xue Q, Bielamowicz S. Direct-numerical simulation of the glottal jet and vocal-fold dynamics in a three-dimensional laryngeal model. J Acoust Soc Am. 2011; 130: 404-415.
  21. Erath BD, Plesniak MW. Impact of wall rotation on supraglottal jet stability in voiced speech. J Acoust Soc Am. 2011; 129: EL64-70.
  22. McGowan RS. An aeroacoustic approach to phonation. J Acoust Soc Am. 1988; 83: 696-704.
  23. Triep M, Brücker C. Three-dimensional nature of the glottal jet. J Acoust Soc Am. 2010; 127: 1537-1547.
  24. Xue Q, Zheng X, Mittal R, Bielamowicz S. Subject-specific computational modeling of human phonation. J Acoust Soc Am. 2014; 135: 1445-1456.
  25. Svec JG, Schutte HK. Videokymography: high-speed line scanning of vocal fold vibration. J Voice. 1996; 10: 201-205.
  26. Zemlin WR. Speech and Hearing Science: Anatomy and Physiology. 3rd edn. Prentice Hall, Englewood Cliffs. 1988.
  27. Scherer RC, Torkaman S, Kucinschi BR, Afjeh AA. Intraglottal pressures in a three-dimensional model with a non-rectangular glottal shape. J Acoust Soc Am. 2010; 128: 828-838.
  28. Guo CG, Scherer RC. Finite element simulation of glottal flow and pressure. J Acoust Soc Am. 1993; 94: 688-700.
  29. Alipour F, Fan C, Scherer RC. A numerical simulation of laryngeal flow in a forced-oscillation glottal model. J. Comput. Speech Language.1996; 10: 75-93.
  30. Pelorson X, Hirschberg A, van Hassel RR, Wijnands APJ. Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation. Application to a midified two-mass model. J. Acoust. Soc. Am. 1994; 96, 3416-3431.
  31. Scherer RC, Shinwari D, De Witt KJ, Zhang C, Kucinschi BR, Afjeh AA, et al. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J Acoust Soc Am. 2001; 109: 1616-1630.
  32. Shinwari D, Scherer RC, DeWitt KJ, Afjeh AA. Flow visualization and pressure distributions in a model of the glottis with a symmetric and oblique divergent angle of 10 degrees. J Acoust Soc Am. 2003; 113: 487-497.
  33. Triep M, Brücker Ch, Schröder W. High-speed PIV measurements of the flow downstream of a dynamic mechanical model of the human vocal folds. Exp. Fluids. 2005; 39: 232-245.
  34. Neubauer J, Zhang Z, Miraghaie R, Berry DA. Coherent structures of the near field flow in a self-oscillating physical model of the vocal folds. J Acoust Soc Am. 2007; 121: 1102-1118.
  35. Luo H, Mittal R, Zheng X, Bielamowicz SA, Walsh RJ, Hahn JK. An immersed-boundary method for flow-structure interaction in biological systems with application to phonation. J Comput Phys. 2008; 227: 9303-9332.
  36. Zheng X, Bielamowicz S, Luo H, Mittal R. A computational study of the effect of false vocal folds on glottal flow and vocal fold vibration during phonation. Ann Biomed Eng. 2009; 37: 625-642.
  37. Zheng X, Mittal R, Bielamowicz S. A computational study of asymmetric glottal jet deflection during phonation. J Acoust Soc Am. 2011; 129: 2133-2143.

Citation: Xue Q, Zheng X and Ye A. Intraglottal Flow Behavior in a CT-Based Laryngeal Model. Austin J Otolaryngol. 2014;1(4): 7. ISSN :2473-0645