Abstract
Mediterranean annual Natural Pastures (NP) constitutes 78% of Portuguese pastures. The alternative - sown pastures with annual legumes mixtures (SC) - is known to have higher productivity and protein content. Several factors might explain why farmers do not adopt this technique fully. One possible explanation, which has not been studied so far, is that farmers use SC just as a complement to NP, thus increasing pasture availability. We tested this hypothesis, using a model to optimize Gross Margin (GM) of sheep production system, according to the proportion of NP: SC areas. The model was based on linear programming, calculating ewe supplementation at minimum cost, in each pasture growth period. Pastures yield and nutritive value data derived from a field trial. A sensitivity analysis of GM to costs, sales and direct ewe subventions was performed. Maximal GM were obtained for areas of 37% SC (subventions not included in returns) or 86% SC otherwise. GM was more sensitive to sales variation than to cost variation. Above the NP: SC corresponding to maximal income, our model showed that GM was highly dependent on sales value. This dependency was attenuated by subventions. Capital investment efficiency decreased with intensification of the production system. In addition, our model showed that production system intensification resulted in a loss of economic robustness of incomes, in relation to costs and sales variation. We suggest these might explain why farmers increase SC area with caution and only in part of their pasture area.
Keywords: Natural pastures; Annual legume pastures; Linear programing; Sheep production systems
Abbreviations
ADF: Acid Detergent Fiber; CAP: Common Agricultural Policy; CP: Crude Protein; DM: Dry Matter; GM: Economic Gross Margin of Activity; LP: Linear Programming; ME: Metabolizable Energy; NP: Natural Pastures; SC: Sown and Improved Pastures, with annual varieties from several species; SR: Annual Stocking Rate (number of ewe ha-1)
Introduction
Permanent Mediterranean rainfed pastures occupy 1,738,185 ha in Portugal, representing 48% of total agricultural surface [1]. These pastures consist in two main types: Natural Pastures (NP) and Cultivated Mixtures (SC) of annual varieties from several species (e.g. Trifolium, Ornithopus, Medicago, Lolium), including optionally perennial drought resistant species (e.g. Phalaris, Dactylis).The first group - NP - represent 78% of the total pasture area, despite its lower productivity (kg Dry Matter ha-1 year-1) and nutritive values. Comparing with NP, the productivity increase induced by SC seems to interact with soil type, fertility and climatic factors: 800 vs. 2087 (sandy soil - low fertility,428 mm rainfall at Coruche) [2], 714 vs.1268 (sandy soil - low fertility, 600 mm rainfall at Canha) [3], 1681 vs 4340 (loamy sandy - medium fertility, 725 mm rainfall at Caria) [2], 3455 vs. 6283 (loamy sandy - medium fertility,1100 mm rainfall at Castelo Branco) [4] and 4100 vs. 7259 (clay loamy - high, fertility and 562 rainfall mm at Elvas) [2].
In the crude protein (CP, i.e. Nx6.25) content in Dry Matter (DM), SC pastures presented an increase in the low to medium soil fertility levels (8% vs. 12% at Coruche and 10% vs. 14%at Caria [2]; 14% vs. 17% at Castelo Branco [5]), but similar to NP at soil high fertility level (18% vs. 17% at Elvas). However, considering nutrient balances (ratios) requirements of grazing sheep (for cheese production), SC mixtures present an unbalanced metabolizable e nergy: CP in some growth periods, dropping nutritional efficiency or posing some animal health risks [7]. In these periods, NP (consisting in native species) could be used to balance ewe nutritional status. One limitation imposed by nutrient content on both NP and SC, is the low fiber content in the first growth periods, expressed by the Acid Detergent Fiber (ADF) fraction in plant tissues - a minimum concentration of 21% ADF in DM intake is required to assure ideal rumen microbe health [8]. Thus, a supplementation with roughages (e.g. hay, straw) to animals grazing NP or SC in periods when pasture has a lower ADF content, could be used to balance diets.
In contrast with higher productivity, SC present specific persistence problems related to the availability of phosphorus in soil [9,10]. Besides, the economy of SC pasture systems poses other difficulties – higher investments and lower capital efficiency [11]. Nevertheless, farmers use some area with SC, to increase pasture availability in particular grazing periods, as a complement of NP. The decision on how much area to dedicate to SC is based on farmer empirical experience, beyond soil, topographic or financial conditions. This reality contrasts with research results, where SC was studied as a full alternative to NP and never as a complement. Therefore, and for the first time, this study aims to investigate the complementarity of NP and SC pastures, by optimizing grazing animal requirements and, considering costs and incomes, maximizing the production system returns.
Linear Programming (LP) has long been used as a powerful decision tool in agricultural systems [12]. It was employed in different situations: e.g. economic evaluation of native pastures [13], optimization of dairy farms [14] or agricultural farms [15], optimization dairy cattle diets in changing policy environmental scenarios [16], effect of agricultural policies on consumers and producer’s welfare [17]. Basically, LP allows to calculate the best combination of limited resources, with the lowest possible cost [18]. In sheep production system sunder Mediterranean conditions, feeding represents a major component of costs and therefore, one basic component of optimization. For that reason, LP was chosen as the basis of a model to estimate the proportion of NP:SC areas, which maximize economic returns. Using the results of a trial on daily growth and nutritive values of NP and SC pastures, grazed by triple aptitude merino sheep, we used LP to achieve ewe supplementation according to nutritional requirements, minimizing supplementation costs, using several scenarios of SC:NP. By calculating then Gross Margin (GM) in each scenario, the production function was established depending on SC proportion of the total pasture area. Our objective was to understand the optimization of the system according to SC:NP and the sensitivity to costs and income variation. In this latter component, we also considered the effect of EU subventions (ewe direct payments) on GM.
Materials and Methods
Pastures experiment
In a randomized complete block design the Natural Pasture (NP) was compared with a sown Subterranean Clover Mixture (SC), in a lithosol under a Mediterranean climate at Castelo Branco, Polytechnic Institute - School of Agriculture farm, Portugal. Total rainfall was 487 mm; annual mean temperature was 15.6°C. Three replicates and 660m-2 plot, were grazed by lactating ewes in five cycles for the growth period of pastures (autumn - end of spring); herbage samples were collected before and after grazing, to determine growth and nutritive value.
Chemical analysis
Fresh samples were dried in a force draught oven at 65°C (±5°C) during 24 hours to constant mass to determine total DM. Samples of pasture, wheat straw, oat hay, maize grain and commercial compound feed were milled and submitted to chemical analysis for CP [19] and Acid Detergent Fiber (ADF) [20]. Metabolizable Energy (ME) for ruminants was calculated by prediction equations [8,21].
Establishment of supplementation quantities
Daily nutritional requirements of a merino ewe (50kg live weight, 0.56kg milk day-1) were considered as: 1.48kg DM intake, 2.82Mcal ME, 153g CP, 31 g ADF and a balance of 53.3g CP Mcal ME-1[8]. A balanced CP:ME ratio will contribute to efficient nitrogen utilization, ideal blood urea level, and consequently reduce nitrogen excretion in urine and faeces [22]. Annual Stocking Rates (SR) - number of ewe ha-1 - for each pasture type and for each combination of NP:SC were derived from 50% total annual DM production [23] divided by annual DM ewe intake. The supplementation needs were obtained for each growth period, through the difference between pasture availability (daily kg DM ha-1 x nutritive value kg-1 DM) and ewe requirements per ha (SR x DM intake ewe-1 x nutrient value kg-1 DM). The solutions for deficits were calculated by LP, using the nutritive values from hay (oats), straw (wheat), grain (maize) and commercial compound feed. These feedstuffs are the most frequently used by farmers in the region, in extensive sheep production systems.
Model and Liner programing
LP provided optimal supplementation solutions at minimum cost [24], for each growth period to the NP, SC or to several scenarios with different combinations of SC:NP. The formulation of these problems has the following structure:

Coefficients (ci, i= 1, …,6) and the decision variables (Xi, i=1, …,6) in the problem, represent the supplementation cost (Kg DM day-1). Variables were NP, SC, hay (oats), straw (wheat), grain (maize) and commercial compound feed. Therefore, equation (1) is the objective function aiming to minimize the result.
Equations (2), (3), (4) and (5) represent the structural problem constraints and (6) the constraints for non-negativity variables. The value of b1, represents the estimate ewe intake (kg DM ha-1 day- 1); b2represents the minimum value that is needed to ensure ewe nutritional requirements - CP(gha-1 day-1), ME (Mcalha-1 day-1), ADF (g ha-1 day-1); b3 represents the maximum availability of NP and SC (kg ha-1 day-1); b4 and b5 are the ratio between CP:ME (minimum and the maximum admissible values). The coefficients a2, a3 and a4, are the contribution associated at each variable, in each constraint referred above.
In the first scenario, supplementation was calculated for 0% SC (or 100% NP). This scenario was solved a second time, entering the SC (growth and nutritive values) as an additional option to the list of supplements. The quantity of SC in the LP solution was then expressed as %, and used for a following scenario with a NP: SC combination. After solving each scenario, the model generate a new scenario with a LP solution of NP: SC. Six different scenarios were generated from the LP primal solutions (0%, 21%, 26%, 33% 67% 100% SC) with different SR, adjusted supplementation quantities and combination from options list, at the minimum cost.
Gross margin calculation
SC and NP pasture costs were estimated considering the variable costs - readily allocated costs which vary in direct proportion to the scale of the enterprise [25]. In SC, the cost included the investment of sowing (sum of machinery, fertilizers, seeds and labor, divided by 10 years of expected pasture persistence) and the annual maintenance cost (sum of machinery, fertilizers, labor); in NP, the cost includes annual maintenance (sum of machinery, fertilizers and labor).
The cost estimation of sheep production system included feeding (pasture and supplementation), veterinary assistance and labor (based on a ratio of 300ewe unit-1), adjusted to each scenario (NP: SC, SR and LP solutions).
Returns were adjusted to each scenario by SR, considering the milk production (daily average of 0.56 Kg ewe-1 for 90 days dairy) and one lamb sold ewe-1 year-1.In addition, but separately, a direct payment of 19€ ewe-1was considered, which is the current Portuguese value of the coupled aid for sheep production within the Common Agricultural Policy (CAP) framework.
All costs and income were estimated using current average market prices (Table 1).
Description
Unit
Price
Observations
Natural pasture – NP
kg DM
0.007 €
13 €/1810 kg
Cultivated pasture -SC
Kg DM
0.037 €
130 €/3470 kg
Straw (wheat)
kg DM
0.079 €
94.4% DM
Hay (Oats)
kg DM
0.112 €
88.9% DM
Grain (maize)
kg DM
0.196 €
86.4% DM
Commercial c. feed
kg DM
0,394 €
89.5% DM
Labor
annual
13,218.00 €
44 €/ewe (300 ewes)
Veterinary
Ewe
1.40 €
Annual
Milk
Lactation/ewe
48.55 €
90 days, 0.56 kg/day
Lamb
Unit/ewe
45.00 €
Table 1: Commodities and products prices, used by LP and optimization modelling.
The financial efficiency of farm enterprise is expressed through the GM which refers to farm total income minus variable costs [25]. GMs were calculated for each scenario. Two regression analyses were used to fit quadratic polynomial function of GM to the proportion of SC variation - including or not, ewe direct payment; the maximum GM value was obtained from these functions.
The sensitivity analysis was performed by re-calculating GM, but varying costs and returns by plus and minus 10% original values. Second-degree polynomials were adjusted and maximum values of functions re-calculated.
Marginal values (GM variation/Cost variation) were used for measuring “capital use efficiency” to compare several scenarios and situations.
Statistical analysis of quadratic polynomial regressions were carried out using t-test, anova and adjusted R2 calculations. The assumptions of data normality and constant variance of residuals were verified using Shapiro-Wilk test and Constant Variance Test, respectively.
Results and Discussion
Grazing supplementation model solutions
Pastures yielded 1,810 kg ha-1in the NP and 3,470 kg ha-1 in the SC. Calculated SR for the several NP:SC combinations in the optimization model were: 3.35 (0% SC), 4.00 (21% SC), 4.15 (26% SC), 4.36 (33% SC) and 5.41(67% SC) and 6.52ewes ha-1(100% SC).
Supplementation estimation for the several pastures scenarios (Table 2) under the restrictions of growth and nutritive values, revealed that fiber (ADF) was the strongest limitation for grazing animals under these Mediterranean systems. In fact, for the 1st, 2nd and 3rd period of growth, the inclusion of a “low cost” fiber (straw) was enough to balance ewes’ nutritive requirements. This unbalance has been observed in similar conditions of climate, pasture type and grazing animals [7]. When NP is combined with SC, LP solutions maximize the use of NP in those periods; this fact might be explained by the lower CP and higher ADF concentrations associated to its lower price. In spring and in the last period of growth, LP solutions maximize the use of SC. In the last period, when pasture is dry, LP solutions combine SC with commercial compound feed, to balance nutrient requirements, despite its higher price (per kg DM), due to its high CP concentration (228g kg DM-1).
7
0%
21%
26%
33%
67%
100%
SR (ewe/ha)
3.35
4.00
4.15
4.36
5.51
6.42
SC (%)
0-100
0-100
0-100
0-100
0-100
0-33
Hay – oats (kg/ha)
-
-
-
-
-
33
Straw- wheat (kg/ha)
286
340
346
350
486
705
Grain – maize (kg/ha)
-
-
-
-
-
-
Commercial c. feed (kg/ha)
75
56
62
66
81
96
GM (€/ha)*
160€
181€
183€
187€
201€
204€
Investment (€/ha)
335€
535€
582€
648€
971€
1285€
*Including ewe direct payment subvention in income.
Table 2: Linear programming solutions and model results for several scenarios of cultivated pastures (SC).
Optimization of NP: SC
The inclusion of SC, can be considered as an intensification of production system since capital use per ha increased directly with %SC (Table 2).
Regressions fit models were significant (P = 0.001) with a very good fit (R2adj=0.9876 and R2adj =0.996, (Figures 1a and b), respectively). Maximum value of GM was obtained with 37% SC (Figure 1a), without considering subventions in income; otherwise it was obtained at 86% SC (Figure 1b) and almost doubled the GM ha-1 (105€ vs. 205€). These first results contrast with those obtained in previous research [2-5] and clearly shows that system optimization is not achieved by full replacement of NP by SC, when both aspects are considered - feeding values and economic results.
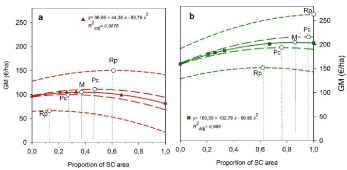
Figure 1: Effect of Sown pasture mixtures (SC) inclusion, as a proportion of
area, on Gross Margin (GM): a Subventions not included in income; b Direct
payments included in income. Sensitivity analysis of GM to ± 10% variation
on sales (short dash, Rp) and on pastures cost (long dash, Pc). Open circles
represent the maximum value to each curve.
Overall, bellow maximization level, GM presented a low sensitivity to costs variation (Figure 1). If SC% increases above maximization level, GM sensitivity to cost variation increases. The variation of sales value was the strongest cause of GM deviation: when subventions were not considered (Figure 1a, Rp) the %SC where maximal GM is obtained shifts from 37% to 13% SC (i.e. 65% reduction); when subventions were included in income (Figure 1b, Rp), the response was attenuated (the % SC where maximal GM is obtained shifts from 86% to 62% SC, i.e. 28% reduction). In fact subventions represent a fixed component of farm income, independent of market behavior. In our model the results showed a smaller GM decrease when subventions were considered (Table 3).This pattern of subventions influence was also observed on cost variations. However, GM was more sensitive to sales than cost variations. Whenever GM varies, independently of cause, a new optimization should be achieved. This optimization would imply a shift on NP:SC (from M to Pc or Rp on Figures 1a and 1b).
Items
No subventions
With subventions
Max
Sales
Cost
Max
Sales
Cost
Total costs (€/ha-1)
315
315
347
468
468
515
Sales (€/ha-1)
420
378
420
560
504
560
Direct payments (€ ha-1)
-
-
-
113
113
113
GM (€ ha-1)
105
63
73
205
149
158
?GM
-42
(-40%)
-32
(-30%)
-56
(-27%)
-47
(-23%)
Table 3: Effect of sales decrease (10%) or costs increase (10%) on maximal GM (Max).
Considering system intensification, in general, our model shows that the return increase is lower than the corresponding investment (Table 2). If we take in account the maximal GM (Figure 2) intensification from 37% SC to 86% SC would require an investment of 465€ ha-1 (data not shown); as a result of this investment GM would increase from 190€ ha-1 to 205€ ha-1. This shift would result in a capital marginal value of 0.03€, i.e. a very low capital efficiency. Therefore, for a farm operating at 37% SC, if we add CAP subventions, it would be reasonable to accept just an increase of income (i.e. from A to C on Figure 2) than a change of NP: SC (i.e. from A to B in Figure 2).This type of subventions results in an aid to income and not as a driver for intensification.
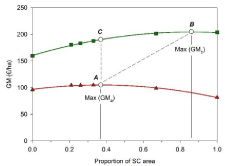
Figure 2: Effect of Sown pasture mixtures (SC) inclusion, as a proportion of
area, on Gross Margin (GM): red and triangles, Subventions not included in
income; green and quadrats, Direct payments included in income.
In a study of Spanish sheep organic farm systems, subventions explain the maintenance of low efficiency farming systems [27] and the authors outlined the need to adjust farm outputs to the available farm resources. This means that intensification requires higher levels of inputs as labor and supplementation but this investment, however, is not returned since input prices grow faster than output prices. Similarly, the effect of the policy tools (EU coupled aid sheep direct payment) considered in our study, suggest a very low effect on stimulation production system intensification (sowing improved pastures and increasing stocking rates). However, it sustains the low input systems, providing an additional income to framers.
Conclusion
Maximization of GM on studied grazing systems is not achieved by replacing the total area of NP with SC. With the current market prices, the financial success of intensification pasture grazing systems relies on subventions. In contrast, the most extensive systems, and particularly below the GM maximization level, presented a higher robustness to cost variation. In addition, the high sensitivity to the variation of sale prices and the low capital use efficiency in the SC, might explain why farmers keep basing the grazing systems on NP.
Attributes like resilience and adaptive capacity are important to understand the maintenance of low efficiency farms [26]. This fact also explains the grazing systems based on NP: despite a lower productivity and profitability they present a better adaptability to changing physical and economic conditions.
References
- INE (Instituto Nacional de Estatística). Dados Estatísticos - Principais Indicadores. 2012.
- Barradas A, Carneiro JP, Amante H, Simoes AM, Olea L, Almeida JPF. Does the response of natural pastures to improvement techniques depend on soil fertility level? Grassland Science in Europe. 2006; 11: 101-103.
- Dordio AM, O’Neill JF, Monteiro AF. Melhoramento de Pastagens Naturais. Resultados de um ensaio no Mio-pliocénico. Pastagens e Forragens. 1991; 12: 115-125.
- Almeida JPF, Fernandes AJG. Improvement of Mediterranean annual type pastures, under covering of olive grove, in Castelo Branco (Portugal). In Proc. 6th Meeting of the FAO. European Sub-Network on Mediterranean Pastures and Fodder Crops, 17-19 October, Bari, Italy, CIHEM, 1990; 69-72.
- Almeida JPF. O Melhoramento de Pastagens de sequeiro em olivais marginais da região de Castelo Branco. Pastagens e Forragens. 1988; 9: 83-94.
- Licitra G, Carpino S, Schadt I, Avondo M, Barresi S. Forage quality of native pastures in a Mediterranean area. Animal Feed Science Technology. 1997; 69: 315-328.
- Molle G, Decandia M, Cabiddu A, Landau SY, Cannas A. An update on the nutrition of dairy sheep grazing Mediterranean pastures. Small Ruminant Research. 2008; 77: 93-112.
- NRC. Nutrient Requirements of Small Ruminants - Sheep, Goats, Cervids and New World Camelids, Washington. National Academic Press. 2007.
- Bolland MDA, Paynter BH. Increasing phosphorus concentration in seed of annual pasture legume species increases herbage and seed yields. Plant and Soil. 1990; 125: 197-205.
- Thomson CJ, Bolger TP. Effects of seed phosphorus concentration on the emergence and growth of subterranean clover (Trifolium subterraneum). Plant and Soil. 1993; 155: 285-288.
- Almeida JPF, Alberto D, Macas BM. Portuguese annual Mediterranean pastures: an economic approach to understand sown pastures failure. Options Mediterraneennes. 2014; 109: 599-602.
- Hazell P, Norton R. Mathematical Programming for Economic Analysis in Agriculture, Mac Millan Publishing Company, New York. 1986.
- Vere DT, Jones RE, Campbell MH. An economic evaluation of native pasturesystems in south-eastern New South Wales. Agricultural Systems. 2002; 72: 133-148.
- Doole GJ, Romera AJ, Adler AA. An optimization model of a New Zealand dairy farm. Journal of Dairy Science. 2013; 96: 2147-2160.
- Fragoso RMS, Carvalho MLS, Henriques PDS. A programação matemática positiva como instrumento de calibração e prescrição dos modelos de oferta agrícola. RevistaInvestigação Operacional. 2008; 28: 1-16.
- Moraes LE, Wilen JE, Robinson PH, Fadel JG. A linear programming model to optimize diets in environmental policy scenarios. Journal of Dairy Science. 2012; 95: 1267-1282.
- Serrão A, Anastácio J. Um modelo de programação matemática aplicado ao sector agrícola português. RevistaInvestigação Operacional. 2003; 23: 17-34.
- Mills G, George Allen, Unwin. Optimisation in Economic Analysis. London .1984.
- AOAC. Official Methods of Analysis, 17th edition. Association of Official Analytical Chemists. 2000.
- Van Soest PJ, Robertson JB, Lewis BA. Methods for dietary fiber, neutral detergent fiber, and nonstarch polysaccharides in relation to animal nutrition. Journal of Dairy Science. 1991; 74: 3583-3597.
- Coppock CE, Gamroth M. Adjusting rations to forage quality, and suggested criteria to use in buying forages. Proceedings of the 3rd Western Dairy Management Conference, Kansas State University. 1997.
- Yan T, Frost JP, Agnew RE, Binnie RC, Mayne CS. Relationships among manure nitrogen output and dietary and animal factors in lactating dairy cows. Journal of Dairy Science. 2006; 89: 3981-3991.
- Dikman J. Carrying capacity: outdated concept or useful livestock management tool? Overseas Development Institute, Pastoral Development Network, FAO. 1998.
- Hillier F, Lieberman G. Introduction to Operations Research. Mc Graw-Hill. 2001.
- DEFRA. Definition of Terms Used in Farm Business Management. London. 2010.
- Toro-Mujica P, García A, Aguilar C, Vera R, Perea J, Angón E. Economic sustainability of organic dairy sheep systems in Central Spain. Ital J AnimSci. 2015; 14: 193-201.
- Ripoll-Bosh R, Díez-UnqueraB, Ruiz R, VillalbaD, Molina E, Joy M, et al. An integrated sustainability assessment of mediterranean sheep farms with different degrees of intensification. Agricultural Systems. 2012; 105: 46–56.
