
Research Article
Austin Biom and Biostat. 2015;2(2): 1016.
Follow-up Design for Comparing Two Binary Diagnostic Tests
Kenta Murotani¹*, Akihiro Hirakawa², Yoshiko Aoyama³ and Takashi Yanagawa³
¹Center for Clinical Research, Aichi Medical University, Japan
²Center for Advanced Medicine and Clinical Research, Nagoya University Hospital, Japan
³The Biostatistics Center, Kurume University, Japan
*Corresponding author: Kenta Murotani, Center for Clinical Research, Aichi Medical University, 1-1 Yazakokarimata, Nagakute, Aichi, Japan.
Received: January 06, 2015; Accepted: May 11, 2015; Published: May 26, 2015
Abstract
Most conventional methods of comparing two diagnostic tests require patients whose true disease statuses are known. We deal with in this paper a problem of comparing two binary diagnostic tests (referred to as new and standard tests) in a follow-up design, where there are no gold standards. Assume that each patient is examined twice by new and standard tests, respectively. We employed a comparison measure ψ, which is compared on the basis of the odds ratio of the new and standard test. It is not possible to estimate ψ from the full likelihood function based on the design, even if two independent multinomial distributions are assumed to the data. Therefore, we focus only on data from discordant pairs between new and standard tests. We construct conditional likelihood conditioned on those pairs and estimate parameters involved in the conditional likelihood. An estimate of ψ is obtained by plugging those estimates in ψ. The asymptotic normality of the estimator of ψ is shown based on delta method and a confidence interval of ψ is developed. A method of sample size determination for this design is also proposed. Simulation is conducted to study the behavior of the proposed method by considering several scenarios.
Keywords: Follow-up design; Diagnostic test; Comparison; No gold standard
Introduction
Accurate diagnosis of the patient is crucial when planning the treatment of a disease. After determining the accurate diagnosis has been determined, the patient can begin receiving adequate treatment. An accurate evaluation and selection of the diagnostic method plays an important role in the patients’ health. A medical method that aims at determining whether a patient is affected by a disease is called a ‘’diagnostic test”. Particularly, diagnostic tests that evaluate the strength of suspicion of certain diseases on binary (‘’positive” and ‘’negative”) are called ‘’binary diagnostic tests”. To determine which of the two binary diagnostic tests is statistically better, the sensitivity and specificity must be closely examined [1,2]. Sensitivity and specificity are defined by the following equation: Sensitivity = Pr (T=1|D=1), Specificity = Pr (T=0|D=0), Where T indicates the diagnostic results according to the binary diagnostic test, and D indicates the actual condition of the disease. The T (D)=1 indicates positivity (disease), and 0 indicates negativity (not disease). Sensitivity is the conditional probability for patients who are actually disease to be diagnosed as positive, and specificity is the conditional probability for patients who are not actually disease to be diagnosed as negative. In both cases, values closer to 1 mean that the diagnostic test is accurate. If an observation of each patient’s actual disease condition (D) is conducted, the sensitivity and specificity can be estimated simply by calculating the proportion.
However, an accurate observation of the value of D involves methods that are often invasive for the patient. In the case of cancers, for example, the value of D can be assessed only by collecting cell samples through biopsy or surgery, and by determining the diagnosis in a comprehensive manner by using pathological and histological methods.
An example of an actual test is that of Berg et al. [3], who performed biopsy in patients with elevated risks of breast cancer for the determination of a definitive diagnosis, to examine whether ‘’mammography alone” and ‘’mammography combined with ultrasound” was effective as diagnostic tests for breast cancer detection. Similarly, in Japan, a large-scale randomized controlled trial of breast cancer screening methods (mammography alone vs. mammography combined with ultrasound) is being conducted on 100,000 women in their 40s [4]. In this study, the definitive diagnosis was determined on the basis of biopsy or surgery for patients whose overall screening results indicated a need for thorough examination. These examples involve two important issues. In other words, when sensitivity and specificity are evaluated directly for comparison, then information related to the definitive diagnosis is required, and the problem is that this imposes a huge burden both on the patient and on the health care workers.
Therefore, in this paper, we propose a methodology for the comparison of two binary diagnostic tests (referred to hereinafter as ‘’new test” and ‘’standard test”) in the absence of a definitive diagnosis, and discuss the follow-up design by using the said methodology. The characteristic of this method is that each patient was twice subjected to the new test and the standard test, respectively, both for a short period and focus was given to findings in which discordant results were obtained from the new and standard tests. This research paper comprises the following: Section 2 summarizes the criteria considered while comparing the two diagnostic tests; Section 3, we propose the methodology; Section 4, numerical simulations are performed using several scenarios; Section 5, a discussion is provided.
Comparison measure
TN,TS ∈{0,1} are random variables representing the results of the diagnosis according to the two binary diagnostic tests, namely the new test and the standard test. Murotani et al. [5] previously summarized the criteria for comparing the standard test and the new test as (C1), (C2), (C3), (C4) as follows:
(C1) Pr(TN=1 |D=1) > Pr(TS=1 |D=1) and Pr(TN=0 |D=0) > Pr(TS=0 |D=0),
(C2) Pr(D=1 |TN=1) > Pr(D=1 |TS=1) and Pr(D=0 |TN=1) > Pr(D=0 |TS=0),
(C3) Pr(TN=1 |D=1) + Pr(TN=1 |D=1) > Pr(TS=1 |D=1) + Pr(TS=0 |D=0), and
(C1) is compared on the basis of the sensitivity and specificity. In (C1) and (C2), the conditions are reversed. In other words, comparison was made on the basis of the probability for the patients actual condition to be ‘’presence of disease” (‘’absence of disease”) when (C2) was diagnosed as positive (negative). Therefore, the diagnostic tests were compared on the basis of their capability to predict the diagnosis. (C3) was compared on the basis of the size of the sum of sensitivity and specificity. This is the equivalent to selecting a diagnostic test with a large Area under the Curve (AUC). (C4) was compared on the basis of the odds ratio of the new test and standard test.
The meanings of the (C4) criteria were as follows: When TN was TN=1, the predictive capacity was expressed as follows:
O1=Pr(D=1 |TN=1)/Pr(D=0|TN=1).
When TN was TN=0, the predictive capacity was expressed as follows:
O2=Pr(D=0 |TN=0)/Pr(D=1|TN=0).
The larger the predictive value of TN=1, the greater the value of O1. The larger the predictive value of TN=0, the greater the value of O2; in other words, the lower the value of O2 -1. Therefore, the ratio of the two (O1/O2) expresses the strength of the relationship between the new test and D. Higher values of the ratio would indicate that the new test is a good diagnostic test. Similarly, the standard test was also defined by the odds ratio, and the (C4) of the new test was compared with that of the standard test on the basis of the meaning of the odds ratio. In this paper, the diagnostic tests were compared on the basis of the meaning of (C4).
The parameters summarizing the (C4) criteria are defined by the following equation:
According to the (C4) criteria, the following interpretations can be made, depending on the value of ψ: {ψ >1 if TN is superior to TS; ψ =1 if TN and TS are equal; ψ <1 is inferior to TS.
Thus, ψ is a criterion for the comparison of the two diagnostic tests.
If ψ can be estimated on the basis of the data, then the two binary diagnostic tests can be compared on the basis of the estimated value. In addition, if the distribution associated with the estimator of ψ can be calculated, then a hypothesis testing pertaining to ψ as well as the estimation of the confidence interval can also be conducted, and a follow-up design for the comparison of two binary diagnostic tests, including the planning of the number of cases, can be proposed. In the absence of definitive diagnosis (in the absence of observation of D), and on the basis of the data obtained by application of the new test and the standard test twice on each patient, the estimate of ψ and its asymptotic distribution were calculated under several assumptions. From the next section, we discuss the methodology in concrete terms.
Methodology
Notation and definition
{TNij(TSij), j=1,2,…,n}was a random variable representing the diagnostic results of the new test (standard test) that the i patient underwent for the jth time; {Di,i=1,2,…,n} was a random variable representing the actual status of the ith individual’s disease. This implies that Di does not depend on j, but the actual status of the disease remained unchanged at the time of the first and second application of the new test and the standard test. This can be ensured by applying the two diagnostic tests in a relatively short period, during which the actual condition of the disease remains unchanged. Di is a non-observed random variable. TNij,TSij, and Di are binary random variables in which 1 means positive (disease) and 0 means negative (not disease). In addition, it was assumed that p=Pr(Di=1) for all i.
The value p represents the prevalence rate. If {eNij,eSij} are considered as instances of TNij,TSij, the data obtained from the application of the new test and standard test twice to n patients without definitive diagnosis are expressed as
The cell probability pikl was ik . In addition, regarding pikl, if the actual condition of the disease is known, then
and for i,j,k and l. were independent of j, but this meant that the cell probability remained unchanged in both the first and the second diagnostic results.
Design based approach
In this section, we consider the probability distribution on the basis of the method of extraction of individuals and to construct the likelihood. The new and standard tests, respectively, were applied twice on the ith patient, and therefore, the jth j=1,2 diagnostic results can be summarized in 2×2 contingency tables. When the twodimensional random variable representing the diagnostic results obtained at the time when the new and standard tests were applied on the ith patient (TNi1,TSi1), and the second diagnostic results of the new and standard tests (TNi2,TSi2) follow a mutually independent multinomial distribution, the likelihood for the ith patient can be expressed in the following equation:
In addition, because the actual status of the disease is unknown, the cell probability pikl will be the mixture probability of the mixing ratio p, as represented by In summary, the overall likelihood function (L) of n patients is provided as follows:
Here qD10i qD01i/qD01i qD10i, does not depend on {i,j} and the results of the new and standard test are mutually independent when conditioned with the actual disease status, ψ can be expressed by the following equation.
When ψ is estimated based on the overall likelihood L, it is important to know whether L is an exponential family. If L is an exponential family, then it is sufficient estimated on the basis of the conditional likelihood of ψ when sufficient sample statistics on nuisance parameters other than ψ are conditioned? However, unfortunately, L is not an exponential family. Therefore, it is difficult to estimate the ψ.
Conditional approach
When the overall likelihood is constructed by assuming the multinomial distribution estimated on the basis of the design, the cell probability will be the mixture probabilities of the not diseased group and that of the diseased group where the prevalence is a mixing ratio. Thus, the overall likelihood was not an exponential family, and it was not possible to estimate ψ based on sufficient statistics. In this section, we limit the data to those used in the analysis, and propose a new approach composed of conditional likelihood functions.
First, we assume the following (E1):
(E1) The data, in which the results of the new test and standard test were consistent with each other, are not related to the comparison of diagnostic tests.
If (E1) is expressed in other words, it insists on the fact that at the time of the analysis, there is no need to take into consideration the data in which the new test and standard test produced the same results. Based on an assumption (E1), considerations are only given to the pairs of data in which the diagnostic results differed from each other (discordant pairs) in the new test and standard test. Therefore, the following sets of A, B1 and B2 are defined depending on the number of times the new test and standard test.
A={i: (TNi1,TSi1, TNi2, TSi2)= (0,1,0,1),(0,1,1,0),(1,0,0,1),(1,0,1,0)},
B1={i: (TNi1,TSi1, TNi2, TSi2)= (0,1,1,0),(0,1,0,0),(1,0,1,1),(1,0,0,0)},
B2={i: (TNi1,TSi1, TNi2, TSi2)= (1,1,0,1),(0,0,0,1),(1,1,1,0),(0,0,1,0)}.
“A” represented a set of individuals in whom the results of the new test and standard test differed from each other, both the first time and the second time they were conducted. B1 (B2) represents a set of individuals in whom the results of the ‘new test’ and ‘standard test’ differed from each other the first time (the second time) they were conducted.
For A∪B1∪B2, T* ij' is defined by the following equation.
where
For i∈A, the observed values of In the same manner, for i∈B1, the observed value of the observed value of In addition, for the ith individual, Mi is defined as Mi=2 for i∈A, and as Mi=1 for i∈B1∈B2. In addition, (A1), (A2), (A3) are assumed as follows:
And are mutually independent.
(A1) assumes that for the ith individual, are mutually independent under the actual status of the disease. Assumptions similar to this have previously been used by Hui and Walter [6] and Yanagawa and Kasagi [7], and are commonly known as conditional independence. Because this assumption is somewhat strong, Vacek [8] and Torrance-Rynard and Walter [9] have examined the effect of the divergence from the assumption on the estimation of the sensitivity and specificity.
(A2) assumes that from the perspective of ' the sensitivity and specificity is constant, and does not depend on i or j. (A3) assumes that each individual is independent of the other individuals. The following important relationship exists between and the two parameters α and β.
This relational equation shows that the conditional maximum likelihood estimator of ψ can be obtained if α and β, which maximize Lc are plugged in into the right side of (2). Under (A1), (A2) and (A3), the conditional likelihood function Lc is provided by the following equation (Appendix 1):
Asymptotic distribution
The α and β, which maximize the Lc are termed . Under such circumstances, the plug-in estimator of ψ is provided by the following equation:
is referred to as Vψ. When actually calculated, the Vψ is a asymptotically given by the following equation.
When the asymptotic normality of and the delta method are used as n→∞ can be derived (Appendix 2), where →L shows a convergence in law.
can be derived (Appendix 2), where →L shows a convergence in law. Using an asymptotic distribution, the 95% confidence interval of ψ is given by the following equation:
Follow-up design
In the previous section, the estimator and asymptotic distribution of Ψ, which was used as an index for the comparison of two binary diagnostic tests, were calculated by focusing on the discordant pairs in the data obtained by applying diagnostic tests twice on patients without definite diagnosis. Here, we would like to describe the design of follow-up trial for the comparison of diagnostic tests using ψ as a primary endpoint. To design a trial, a known distribution of the primary endpoint is required.
The asymptotically, and the tested hypothesis is the following: H0: logψ=0 vs. H0: logψ≠0. This is the framework of a standard single-arm trial. If the values of logψ and Vψ, and the level of significance and power are fixed, then the sample size needed for the detection of differences will be determined. However, because Vψ is a quantity, which is difficult to understand intuitively, it can be predicted that Vψ may be difficult to estimate during the design phase. To prevent this, we propose that the trial be started without determining Vψ, and that Vψ is estimated at a time when an n0 number of individuals have been accumulated after the beginning of the trial, and that the sample size needed for the detection of the differences be designed by using the estimate of variance. The order of the Vψ can be evaluated according to the following equation:
Where, A is a constant. After the beginning of the trial, an estimation of the variance is performed at a time when an n0 number of individuals have accumulated, and the resulting value is termed Vψ0. In such cases, the variance can be estimated according to the below equation, at a time when an n1 number of cases have been accumulated for an arbitrary n1>n0.
Based on the above, when considering logψ1 as the difference to detect, Zk as the upper-tail percentage points for the standard normal distribution, a as the level of significance, and 1 - b as the power, the sample size (n1) needed for the detection of the difference with a probability higher than 1 - b can be designed according to the following equation,
Using the approximation of we obtain the following equation,
Simulation
Several concrete situations are designed, and the behavior of the according to the proposed method was examined numerically. Pr(TN,TS|D=1) and Pr(TN,TS|D=0) as well as the prevalence p=Pr(D=1) were put. Here, pattern 1 to pattern 4 was taken into account (Table1).
The differences between the patterns depended on 4 combinations involving whether the prevalence was high (low), and whether the new test was better (worse) than the standard test. In pattern 1, the prevalence was low (p=0.05), and the new test inferior to the standard test (logψ < 0). In pattern 2, the prevalence was high (p=0.2), and the new test inferior to the standard test (logψ < 0). In pattern 3, the prevalence was low (p=0.05), and the new test superior to the standard test (logψ > 0). In pattern 4, the prevalence was high (p=0.2), and the new test superior to the standard test (logψ > 0). The true values of α,β and ψ were calculated based on (1), (2), and the true conditional probability established in Table 1. In pattern 1, for example, α=0.2/ (0.2+0.15)=0.57, β=0.1/(0.1+0.2)=0.67, ψ=(0.57×0.333)/(1-0.57)×(1- 0.33)=0.67, logψ=log(0.67)=-0.41. The true values of α,β,ψ and logψ in other patterns are summarized in Table 2.
Pr((TN,Ts)ID = 1)
Pr((TN,Ts)ID = 0)
Pattern
p
(0,0)
(0,1)
(1,0)
(1,1)
(0,0)
(0,1)
(1,0)
(1,1)
1
0.05
0.1
0.15
0.2
0.55
0.6
0.1
0.2
0.1
2
0.2
0.1
0.15
0.2
0.55
0.6
0.1
0.2
0.1
3
0.05
0.1
0.05
0.15
0.7
0.5
0.2
0.1
0.2
4
0.2
0.1
0.05
0.15
0.7
0.5
0.2
0.1
0.2
Table 1: Combination of the true probability of occurrence and true prevalence.
Pattern
α
β
Y
Log Y
1, 2
0.57
0.33
0.67
-0.41
3, 4
0.75
0.67
6
1.79
Table 2: The true values of α, β, ψ and Log ψ.
For each pattern, data composed of random numbers were generated, a set consisting of A, B1 and B2 was formed, and data sets consisting exclusively of discordant pairs were generated. Next, maximizing the likelihood (3) were calculated; the estimate ψ was calculated on the basis of and logψ was calculated. The calculation was repeated 1,000 times, and the sample mean of the estimates of logψ, Standard Error (SE), bias and Mean Squared Error (MSE) were calculated. A bias was defined as a subtraction of the true value from the sample mean. In other words, if the bias had a positive value, it showed an overestimate, and if it had a negative value, then it showed an underestimate. The sample size extracted at the beginning was set to n= 500, 1000, 2000, 5000, and 10,000 (Note that this is not the number of discordant pairs). All calculations were performed using the statistical software R (Ver. 3.1.1). The results were as follows.
In patterns 1 and 2, the new test was bad (true log=- 0.41) the prevalence p was p=0.05 in pattern 1 and p = 0.2 in pattern 2. The prevalence was the only parameter that showed a difference between both the patterns. The results of the estimations are summarized in Table 3. Even when $n$ is increased, the bias is not stable in pattern 1. Except for n=2000, a slight tendency to overestimate was found. On the other hand, the bias in pattern 2 is more unstable than that of pattern 1. MSE was lower in pattern 2 than in pattern 1, and estimations showing better accuracy at high prevalence were conducted. Next, we show the results of pattern 3 and pattern 4.
Pattern 1 (p= 0.05)
Pattern 2 (p= 0.20)
n
mean
s. e.
bias
MSE
mean
s.e.
bias
MSE
500
-0.493
0.022
-0.088
1.094
-0.462
0.019
-0.056
11808
1000
-509
0.021
-0.103
0.997
-0.392
0.018
1014
0.7
2000
-0.384
0.021
0.021
0.949
-0.421
0.016
-0.016
0.586
5000
-11409
0.019
-0.003
0.78
-0.342
0.015
0.063
0.48
10000
-0.427
0.017
-0.021
0.67
-0.348
0.013
0.057
395
Table 3: Results of the simulation of pattern I and pattern 2.
For pattern 3 and pattern 4, the new test was superior to the standard test (true log=1.79); and the prevalence p was p=0.05 in pattern 3 and p = 0.2 in pattern 4. The accuracy was higher with pattern 4 than with pattern 3 (i.e. high prevalence leads to the reduction of S.E.). In addition, for both patterns 3 and 4, an increase in sample size was accompanied by a tendency to averagely underestimate logψ. The numerical results from Tables 3 and 4 are summarized in Figure 1. The error bars in the figure show the 95% confidence interval for the mean, and the dotted line represents the true value of logψ. The lower half corresponds to patterns 1 and 2, and the upper half corresponds to patterns 3 and 4. Triangles show values in case of p=0.05; circles show values in case of p=0.2 (Figure 1).
n
Pattern 3 (p = 0.05)
Pattern 4 (p=0.20)
mean
s. e.
bias
MSE
mean
s.e.
bias
MSE
500
2.312
0.078
0.52
0.437
1.824
0.036
0.033
0.037
1000
1.993
0.042
0.201
0.088
1.68
0.024
-0.112
0.028
2000
1.659
0.026
-0.133
0.037
1.571
0.017
-0.22
0.056
5000
1.567
0.02
-0.225
0.062
1.515
0.011
-0.277
0.08
10000
1320
0.016
-0.272
0.081
131.4
11008
-0.278
0.079
Table 4: Results of the simulation of pattern 3 and pattern 4.
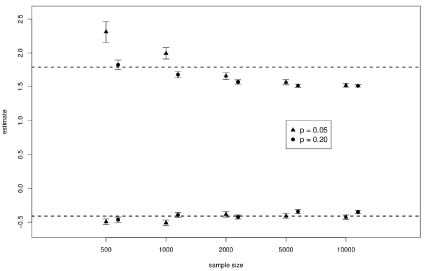
Figure 5: Sample mean and 95%confidence interval of the estimated values
of log in each Pattern.
Discussion
In this paper, we propose a parameter ψ for the comparison of diagnostic tests on the basis of data obtained from the application of each binary diagnostic test twice in patients with no definitive diagnosis. The asymptotic distribution of logψ was also calculated on the basis of conditions in which the data were limited to discordant pairs; further, the method for designing the sample size was also discussed. The influence of the restricted focus on discordant pairs on the estimation results is probably an issue that will need to be evaluated in the future. Comparisons with the estimation of logψ from the overall likelihood can be conducted, but when the estimation is based on the overall likelihood, then the number of parameters increases and application of the diagnostic tests twice in each individual does not allow for a sufficient degree of freedom and makes it impossible to conduct simultaneous estimation of all parameters. In this way, for estimating all parameters, the necessary for application of the diagnostic tests for estimating all parameters between the proposed method and the overall likelihood based method is different. Therefore, a comparison between two approaches is complicated.
The results of the numerical simulation showed an average tendency to underestimate when the true value of logψ was positive. The fact that logψ was positive implied that the conditions were more excellent with the new test than with the standard test. From a researchers’ perspective, trials can be carried out with certitude that the new test is a better diagnostic test than the standard test. This is believed to pose no particularly major problem because even if the new test is actually good, it can be interpreted as comparing conditions in a conservative manner. However, the theoretical reasons for underestimating need to be further evaluated. When the simulation results were discussed on the basis of the relationship with prevalence, the estimations were more highly accurate when the prevalence was high than when it was low. When the prevalence was high, individuals with D =1 were potentially included in large numbers. For such individuals, the accuracy of the estimation of parameters (α) conditioned at D =1 was higher, and as a result, the accuracy of logψ was considered to improve.
Our methodology allows designing the necessary number of cases at a time when n0 individuals have been accumulated after the start of the trial. In such cases, the problematic issue comprises ‘’what the value of n0 should be in order to be considered sufficient;” but the results of numerical simulations have shown that even in the worst case (pattern 3 and n=500), the SE of logψ was about 0.078. Therefore, the evaluation of dispersion might be good if performed at n0=500.
This study was conceived exclusively for patients without a definitive diagnosis; however, after the start of the trial, we expected that while the trial was underway, the definitive diagnosis of some individuals might be determined. With the current methodology, there is no other choice but to conduct analyses by treating such individuals in the same manner as those whose definitive diagnosis has not yet been determined are treated. However, it is also beneficial to estimate information pertaining to the definitive diagnosis in mid-course of the trial and to develop a methodology allowing for estimation that is more accurate. This issue will be the topic of another paper.
References
- Pepe MS. The Statistical Evaluation of Medical Tests for Classification and Prediction. New York: Oxford University Press. 2003.
- Jin H, Lu Y. A non-inferiority test of areas under two parametric ROC curves. Contemp Clin Trials. 2009; 30: 375-379.
- Berg WA, Blume JD, Cormack JB, Mendelson EB, Lehrer D, Bohm-Velez M, et al. Combined screening with ultrasound and mammography vs mammography alone in women at elevated risk of breast cancer. JAMA. 2008; 299: 2151-2163.
- Ohuchi N, Ishida T, Kawai M, Narikawa Y, Yamamoto S, Sobue T. Randomized controlled trial on effectiveness of ultrasonography screening for breast cancer in women aged 40-49 (J-START): research design. Jpn J Clin Oncol. 2011; 41: 275-277.
- Murotani K, Aoyama Y, Nagata S, Yanagawa T. Exact method for comparing two diagnostic tests with multiple readers based on categorical measurements. J Biometrics. 2009; 30: 69-79.
- Hui SL, Walter SD. Estimating the error rates of diagnostic tests. Biometrics. 1980; 36: 167-171.
- Yanagawa T, Kasagi F. Estimating prevalence and incidence of disease from a diagnostic test. Statistical Theory and Data Analysis, Amsterdam: Elsevier. 1985.
- Vacek PM. The effect of conditional dependence on the evaluation of diagnostic tests. Biometrics. 1985; 41: 959-968.
- Torrance-Rynard VL, Walter SD. Effects of dependent errors in the assessment of diagnostic test performance. Stat Med. 1997; 16: 2157-2175.