Size and Power of Tests of Hypotheses on Survival Parameters from the Lindley Distribution with Covariates

Abstract

The Lindley model is considered as an alternative model facilitating analyses of time-to-event data with covariates. Covariate information is incorporated using the Cox’s proportional hazard model with the Lindley model as the timedependent component. Simulation studies are performed to assess the size and power of tests of hypotheses on parameters arising from maximum likelihood estimators of parameters in the Lindley model. Results are contrasted with that arising from Cox’s partial maximum likelihood estimator. The Lindley-Cox model, is used to analyze a publicly available data set and contrasted with other models.

Keywords: Lindley distribution; Lindley-Cox model; Hazard function;

Introduction and Definitions

The Lindley distribution [1] was introduced in connection with fiducial distribution and the Bayes’ theorem, but it has not been widely utilized for analyses of time-to-event data until the past decade when Ghitany et al. [2] explored its mathematical properties and real data applications in time-to-event settings. However, to the best of our knowledge the Lindley distribution has not been considered in connection with the incorporation of covariate information.

Covariate information and times-to-event are collected on subjects in time-to-event studies (e.g., time-to-death or survival time). Such data are often analyzed by choosing a suitable model for the times-to-event that allows covariates to be utilized in the statistical analyses. The analyses proceed by estimating parameters in the model and testing hypotheses about those parameters based on their estimates. The validity and reliability of inferences from tests of hypotheses about parameters depend on the size and power of the tests.

We motivate incorporation of covariate information using the Lindley distribution as the time-dependent component of the Cox’s proportional (Cox’s PH) model with the data set provided by Freireich et al. [3]. The data set contains survival times and White Blood Cell (WBC) information on a small number of patients. With such a small sample, the efficiency of the partial maximum likelihood estimates of the Cox’s proportional hazard model may not be optimal [4-6].

The relationship among hazard rate function h(t), survival function S(t), death density function f(t), and death distribution function F(t) is important in describing time-to-event probabilities of a population. If the hazard rate h(t) function is given, then the survival function S(t) is

$S\left(t\right)=\exp \left[-\underset{0}{\overset{t}{{\displaystyle \int }}}h\left(u\right)du\right]\text{ (1)}$

and

$f\left(t\right)=h\left(t\right)S\left(t\right)=\frac{-d[S(t)]}{dt};\text{ (2)}$

F(t)=1-S(t) (3)

Accordingly, if one knows any of the functions, one could determine the remaining three.

The cox proportional hazard model

Cox [7] considered a distribution-free approach that incorporates covariates, in which the main purpose of survival times is to keep track of the covariate information [4]. Assuming arbitrary baseline hazard, Cox proposed the hazard function

$h\left(t;X,\text{Θ},\beta \right)=h_0\left(t;\text{Θ}\right)\exp \left(X^{\text{'}}\beta \right),\text{ (4)}$

where X=(x1,x2,…,xp) is a vector of p-covariates, β=(β1, β2,…, βp) is the corresponding vector of unknown parameters, h₀(t;θ) is the baseline hazard (a function of time only), and θ is the parameter vector of the baseline hazard function. Under Cox’s proportional hazard model, no assumption is made about the specific form of the baseline hazard function, and interest is on assessing the association between the survival times and covariate information. He estimated the covariate parameter vector β by maximum likelihood that is conditional on risk sets of instances of event occurrence.

Cox [7] noted that a major problem is the assessment of asymptotic relative efficiency of tests on covariate parameters under various assumptions about h₀(t;θ). Some authors addressed this problem for specific forms of h₀(t;θ) [4,5,8,9] . For a single covariate (i.e, p=1), Kalbfleisch [8] suggested that the exponential and Weibull forms for h₀(t;θ) do not provide significantly greater efficiency than Cox’s procedure in most practical settings. Kalbfleisch’s results suggested that covariates and their coefficients affect the efficiency properties of Cox’s estimator. Efron [9] maintained that the full maximum likelihood estimator of β is asymptotically equivalent to Cox’s partial likelihood estimator of β—by showing that Fisher’s information for β (for p=1) using the entire data is asymptotically equivalent to that calculated from Cox’s model.

Specific hazard function as the time-dependent component of the Cox’s proportional hazard model

Many authors proposed distribution-based methods that incorporate covariates in modeling time-to-event data; see for example [5,10-12].

Specifying h(t;X,θ,β)= h(t;θ) exp(X'β) and h(t;θ) to be a specific parametric hazard function yields a parametric model with the death density function f(t; θ, X, β)= h(t;θ,X,)S(t;θ,X,β),

$S\left(t;\theta ,X,\beta \right)=\exp \left(-\underset{0}{\overset{t}{{\displaystyle \int }}}h\left(u;\theta ,X,\beta \right)du\right)\text{ (5)}$

This formulation enables parameters in the time-dependent component and covariate parameters of the hazard rate function to be estimated and attendant inference made using (full) maximum likelihood methods.

Many authors considered models with specific forms of h₀(t;θ), the time-dependent component of the hazard function [4,5,12-15] under various assumptions. The exponential, Weibull, and Gompterz are examples of such models. Peace and Flora [4] and Peace [5] assessed the efficiency (size and power) of tests of hypotheses on covariate parameters by assuming the exponential, Weibull, Gompterz, and Rayleigh models (parametric with covariates) for the time-dependent component of Cox’s model using full maximum likelihood theory as compared to those from using Cox’s model and partial maximum likelihood method of estimation. They suggested that if interest is solely on β, choosing any of the considered parametric models as the first step in analyzing time-to-event data may not worth the effort; they recommended Cox’s method for analyses, except for small samples (n=25). They, however, recommended exponential model (when it fits the data) over Cox’s for assessing global null hypotheses. Their recommendations derive from the parametric models having, on average, larger power than Cox’s for small samples-particularly for tests concerning one covariate parameter.

We consider the Lindley model as an alternative model facilitating the analyses of time-to-event data with covariates. Such a consideration reflects an extension of [4] and [5] in comparing tests of hypotheses on time-to-event parameters from Cox’s Model and method of estimation with those from fully parametric methods for the Lindley-Cox model using simulation studies. Covariate information is incorporated using the Cox’s proportional hazard’s model with the Lindley model as the time-dependent component (referred to as the Lindley-Cox model). This mixture model is relatively recent and has not seen applications in the analyses of time-to-event data with covariates. Specifically, we (1) perform simulation studies to assess the size and power of tests on parameters arising from Maximum Likelihood Estimates (MLEs) of β in the Lindley-Cox model, and (2) contrast the results of size and power of tests on β arising from Lindley-Cox MLEs with those arising from Cox’s partial maximum likelihood estimator. In addition, we analyze a publicly available data set using the Lindley-Cox model and contrast our findings with results from other models.

Methods

The Lindley model as the time-dependent component of the Cox’s PH

With the formulation in the peceding section, specifying the Lindley hazard and survival functions with covariate gives

$h\left(t;X,\theta ,\beta \right)=\frac{{\theta }^2\left(1+t\right)}{\theta +1+\theta t}\exp \left(X^{\text{'}}\beta \right),\text{ (6)}$

and

S(t;X,θ,β)= exp(-exp(X’β)(θt_i-In(θt_i+θ+1)+In(θ+1))) , (7)

respectively, and the Lindley-Cox death density function:

$f_l(\theta ,\beta )=\left[\frac{{\theta }^2\left(1+t_i\right)}{\theta +1+\theta t_i}\exp \left(X_i^{\text{'}}\beta \right)\right]$$\left[\exp \left(-\exp \left(X_i^{\text{'}}\beta \right)(\theta t_i-\ln \left(\theta t_i+\theta +1\right)+\ln \left(\theta +1\right)\right))\right],\text{ (8)}$

where θ represent the scale parameter of the Lindley distribution.

Denote the observed and censored event times by t_i (i=1,2,…,d) and T_k (k=1,2,…,c=n-d), respectively. The log-likelihood for the Lindley-Cox model is

$\ln L_l(\theta ,\beta )=$$\{n\ln {\theta }^2+{\displaystyle \sum }_{i=1}^d\ln \left(1+t_i\right)-{\displaystyle \sum }_{i=1}^d\ln \left(\theta +1+\theta t_i\right)+{\displaystyle \sum }_{i=1}^d{X}_i^{\text{'}}\beta$$-{\displaystyle \sum _{i=1}^d\left[\text{exp}\left(X_i^{\text{'}}\beta \right)\left(\theta t_i-\ln \left(\theta t_i+\theta +1\right)+\ln \left(\theta +1\right)\right)\right]}\}$$-{\displaystyle \sum }_{k=d+1}^n\left[\text{exp}\left(X_k^{\text{'}}\beta \right)\left(\theta T_k-\ln \left(\theta T_k+\theta +1\right)+\ln \left(\theta +1\right)\right)\right]\text{ (9)}$

The MLEs of θ and β may be found iteratively. The asymptotic covariance matrix of the estimators is approximately

$-{\left[\frac{{\partial }^2\ln L_l}{\partial \theta \partial \beta }\right]}_{t\times t}^{-1},\text{ (10)}$

where β=(β₁, β₂,…, β_p), and t=p+1.

Test of hypotheses

The tests of hypotheses investigated are

H₀: Lβ=β₀ (11)

and

H₀: β_q=β_0q, q=1,2,…,p, (12)

where β_q and β_0q are the qth components of β and β₀, respectively, and L represents a matrix of coefficients for the linear hypotheses, and β₀ is a vector of constants.

These tests of hypotheses may be achieved using asymptotic likelihood inference: the Wald, the score, and likelihood ratio test statistics, which are approximately low-order Taylor series expansion of each other [16]. These three test statistics are asymptotically equivalent with possible differences among them in finite samples; in which case, the likelihood ratio test is generally deemed most reliable. Since the likelihood ratio test and Wald test are more commonly used, these two tests are presented in this study.

Denote the Likelihood Ratio (LR) statistics by Λ. Let $\stackrel{}{\stackrel{\wedge }{V}}(\stackrel{}{\stackrel{\wedge }{\beta }})$ be the estimated covariance matrix of $\stackrel{\wedge }{\beta }$ . The statistics, based on asymptotic properties of $\stackrel{\wedge }{\beta }$ (Given a non-singular covariance matrix), for testing the H₀ in Equation 11 is

$T=\left(L\stackrel{}{\stackrel{\wedge }{\beta }}-{\beta }_0\right){\left[L\stackrel{}{\stackrel{\wedge }{V}}(\stackrel{}{\stackrel{\wedge }{\beta }})L\text{'}\right]}^{-1}\left(L\stackrel{}{\stackrel{\wedge }{\beta }}-{\beta }_0\right)\text{. (13)}$

Under H₀,$-2\ln \text{Λ}$ and T are asymptotically (AN) distributed as chi-square with r degrees of freedom, written $-2\ln \text{Λ~}{\chi }_{(r)}^2$ and $T\text{~}{\chi }_{(r)}^2$ where r represents the rank of r in the case of T and the number of parameters under the alternative hypothesis minus that under the null hypothesis in the case of LR. For the hypothesis in Equation 12, the test statistic in Equation 13 reduces to a univariate case

$T_{0q}={\left[{\stackrel{}{\stackrel{\wedge }{\beta }}}_q-{\beta }_{0q}\right]}^2{\left[\stackrel{}{\stackrel{\wedge }{V}}({\stackrel{}{\stackrel{\wedge }{\beta }}}_q)\right]}^{-1},\text{ (14)}$

where ${\stackrel{}{\stackrel{\wedge }{\beta }}}_q$ represents the q^th component of β, and $\stackrel{}{\stackrel{\wedge }{V}}({\stackrel{}{\stackrel{\wedge }{\beta }}}_q)$ is the qth diagonal element of $\stackrel{}{\stackrel{\wedge }{V}}({\stackrel{}{\stackrel{\wedge }{\beta }}}_{})$$T_{0q}\text{~}{\chi }_{(1)}^2$

Generating Lindley-Cox times-to-event with covariates

Suppose U_i (i=1,2,…,n) are random numbers, times-to-event (tⁱ) may be obtained by solving the following equation (Equation 15) of the cumulative hazard H(t_i) for (t_i) [4,5,17-20]

$H(t_i)={\displaystyle \underset{0}{\overset{t_i}{\int }}{h}_0(w)dw}=-y_i,\text{ (15)}$

where h₀ is the baseline hazard rate function, and

$y_i=\left[\exp (-X_i^{\text{'}}\beta )\right]\left[\ln \left(1-u_i\right)\right];\text{ (16)}$

U_i is a uniform random variable, Xi=(x₁,x₂,…,x_p) is a p-component row vector of covariates, and β=(β₁, β₂,…, β_p) is the p parameter vector corresponding to X₁. The ti’s are obtained by solving for t_i in the nonlinear equation that results from replacing h₀ in Equation 15 with the Lindley hazard function, given by

$h\left(t;\theta \right)=\frac{{\theta }^2\left(1+t\right)}{\theta +1+\theta t},\theta >0,t\ge 0.\text{ (17)}$

Times-to-event are generated by specifying the covariate vector Xi, which is fixed by design; the parameters (θ and β) used in generating the event times are chosen to mirror the data set to be analyzed by the authors. The number of components of X_i, p, is chosen to be 6, and the components of p are selected at random using the following conditions: 14<x₁<70, 0<x₂<99, x₃=1,2, or 3 and x₄=x₅=x₆=0 or 1 The dichotomous covariate information x4,x5 and x6 are selected such that the proportions of 1 in x4,x5 and x6 are approximately 20%, 40%, and 60%, respectively. Parameter values are chosen to be (θ=0.4, β₁=1.3, β₂=0.08, β₃=0.6, β₄0.8, β₅=0.4, β₆=1.2).

It is assumed that a sample of N independent, observable survival times (t₁,t₂,…,t_N) are the available information on a population; of those, d (d<=N) are the observed times of the event, and the remaining k=N-d are right censored. The censoring distribution is assumed to follow the Lindley distribution. As an assessment of the sensitivity of the model to the censoring distribution, another set of assessments was performed by simulating the censoring distribution according to a Linley-Cox distribution with different values of the hazard function and the results were similar to those presented. The same data sets are used in assessing size and power; however, in assessing power, new hypotheses produced by inducing 20% deviation of the parameter values are tested.

Size and power are relative to the null hypotheses–the null being the statement that the parameters are equal to the values that were used to simulate the data. Size is the probability of rejecting the null given the null is true. Power is the probability of rejecting the null given the null is false; adding 20% deviation to simulation parameters means null is false, hence a question of power. This percentage deviation stems from the fact that many clinical studies aim to detect a minimum of 20% difference between treatment and control groups.

In assessing size and power of tests of hypotheses, m=5,000 independent data sets are generated for each sample size (n=25,50,100,250,500,1,000). Newton Raphson method, with 10^-8 convergence criteria, is used to obtain the maximum likelihood estimates prior to assessing the size and power of tests. Simulations and analyses are performed using SAS/STAT software version 9.4 of SAS system for Windows. Copyright 2011 SAS Institute Inc. SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc., Cary, NC, USA. Graphics are generated using R software 2.14.

Results and Comments

Results

Size of tests of hypotheses: T?he null parameter values and nature of the covariates for assessing size of tests for the Lindley-Cox and Cox PH models are mentioned in section 4.3. The null parameter values are those used in generating t_i’s that followed the Lindley-Cox distribution.

The proportion ${\stackrel{}{\stackrel{\wedge }{\alpha }}}_s=T_s\text{.}/m$ = (s=c,l) represents the estimated size of test or false positive rates, where T_s denotes the number of times the tests rejected H₀ out of m replicates. (Tests from Cox’s and Lindley- Cox models are indexed by c and l, respectively). Tables 1 & 2 show the size of tests of hypotheses in percent (i.e., $100\times {\stackrel{}{\stackrel{\wedge }{\alpha }}}_s$ ) for the tests of hypotheses described in section 4.2. Table 1 presents the results for complete data, whereas Table 2 presents the results for 20% censored data.

Table 1: Estimated Size of Tests on Covariate Parameters Based on Cox’s and the Lindley-Cox Models with Complete Data.

  

    
H0:b=b0 
  
  

    
 
    
Sample Size (n)
  
  

    
Model
    
25
    
50
    
100
    
250
    
500
    
1,000
  
  

    
 
  
  

    
Lindley-Cox I
    
5.30
    
4.72
    
4.80
    
4.88
    
5.04
    
4.92
  
  

    
CI
    
4.68, 5.92
    
4.13, 5.31
    
4.21, 5.39
    
4.28, 5.48
    
4.43, 5.65
    
4.32, 5.52
  
  

    
Lindley-Cox II
    
7.76
    
5.74
    
5.46
    
5.26
    
5.28
    
5.00
  
  

    
CI
    
7.01, 8.50
    
5.10, 6.38
    
4.83, 6.09
    
4.64, 5.88
    
4.66, 5.90
    
4.40, 5.60
  
  

    
Cox I
    
11.80
    
7.32
    
5.70
    
5.34
    
5.66
    
5.44
  
  

    
CI
    
10.91, 12.69
    
6.61, 8.08
    
5.06, 6.34
    
4.72, 5.96
    
5.02, 6.30
    
4.81, 6.07
  
  

    
Cox II
    
7.58
    
6.66
    
5.70
    
5.78
    
5.78
    
5.42
  
  

    
CI
    
6.86, 8.35
    
5.97, 7.35
    
5.06, 6.34
    
5.13, 6.43
    
5.13, 6.43
    
4.79, 6.05
  
  

    
H0:b1=b01 
  
  

    
 
  
  

    
Lindley-Cox I
    
5.41
    
4.66
    
4.98
    
4.92
    
5.22
    
5.74
  
  

    
CI
    
4.78, 6.04
    
4.08, 5.24
    
4.38, 5.58
    
4.32, 5.52
    
4.60, 5.84
    
5.10, 6.38
  
  

    
Lindley-Cox II
    
5.83
    
4.84
    
4.86
    
4.84
    
5.38
    
5.86
  
  

    
CI
    
5.18, 6.48
    
4.25, 5.43
    
4.26, 5.46
    
4.25, 5.43
    
4.75, 6.01
    
5.21, 6.51
  
  

    
Cox I
    
10.52
    
7.02
    
5.80
    
5.54
    
5.80
    
5.84
  
  

    
CI
    
9.67, 11.37
    
6.31, 7.73
    
5.15, 6.45
    
4.91, 6.17
    
5.15, 6.45
    
5.19, 6.49
  
  

    
 
    
Cox II
    
8.96
    
6.56
    
5.42
    
5.62
    
5.64
    
5.74,
  
  

    
CI
    
8.17, 9.75
    
5.87, 7.25
    
4.79, 6.05
    
4.98, 6.26
    
5.00, 6.28
    
5.10, 6.38
  

Table 1:  Estimated Size of Tests on Covariate Parameters Based on Cox’s and
the Lindley-Cox Models with Complete Data.

Close

Table 1: Note: Values of ${\stackrel{}{\stackrel{\wedge }{\alpha }}}_s=100\times T_s\text{.}/ms$ (s=c,l), where T_s is the number of times the tests rejected H₀ out of m=5,000 replicates for different sample sizes with complete data. Tests are run at α=0.05. I and II denote Likelihood ratio and Wald chi-square, respectively. CI=95% confidence interval; L-Cox=Lindley-Cox model.

Table 2: Estimated size of tests on covariate parameters based on Cox’s and the Lindley-cox models with 20% censored data.

  

    
H0:b=b0 
  
  

    
 
    
Sample Size  
  
  

    
Model
    
25
    
50
    
100
    
250
    
500
    
1,000
  
  

    
 
  
  

    
Lindley-Cox I
    
6.28
    
5.92
    
4.88
    
5.04
    
5.32
    
5.30
  
  

    
CI
    
5.61, 6.95
    
5.27, 6.27
    
4.28, 5.48
    
4.43, 5.65
    
4.70, 5.94
    
4.68, 5.92
  
  

    
Lindley-Cox II
    
8.11
    
6.24
    
5.58
    
5.04
    
5.32
    
5.34
  
  

    
CI
    
7.35, 8.87
    
5.57, 6.91
    
4.94, 6.22
    
4.43, 5.65
    
4.70, 5.94
    
4.72, 5.96
  
  

    
Cox I
    
11.96
    
7.90
    
5.94
    
5.04
    
5.08
    
5.50
  
  

    
CI
    
11.06, 12.86
    
7.17, 8.67
    
5.28, 6.60
    
4.43, 5.65
    
4.47, 5.69
    
4.87, 6.13
  
  

    
Cox II
    
5.56
    
6.52
    
5.90
    
5.24
    
5.10
    
5.44
  
  

    
CI
    
4.92, 6.20
    
5.84, 7.20
    
5.25, 6.55
    
4.62, 5.86
    
4.49, 5.71
    
(4.81, 6.07)
  
  

    
H0:b1=b01 
  
  

    
 
  
  

    
Lindley-Cox I
    
6.18
    
5.66
    
5.44
    
5.22
    
5.14
    
5.26
  
  

    
CI
    
5.51, 6.86
    
5.02, 6.30
    
4.81, 6.07
    
4.60, 5.84
    
4.53, 5.75
    
4.64, 5.88
  
  

    
Lindley-Cox II
    
6.35
    
5.80
    
5.20
    
5.24
    
5.14
    
5.36
  
  

    
CI
    
5.67, 7.03
    
5.15, 6.45
    
4.58, 5.82
    
4.62, 5.86
    
4.53, 5.75
    
4.74, 5.98
  
  

    
Cox I
    
11.12
    
7.76
    
6.12
    
5.58
    
5.76
    
5.54
  
  

    
CI
    
10.25,11.99
    
7.02, 8.50
    
5.46, 6.78
    
4.94, 6.22
    
5.11, 6.41
    
4.91, 6.17
  
  

    
Cox II
    
8.82
    
7.12
    
5.88
    
5.48
    
5.62
    
5.44
  
  

    
CI
    
8.03, 9.61
    
6.41, 7.83
    
5.23, 6.53
    
4.85, 6.11
    
4.98, 6.26
    
4.83, 6.07
  
  

    
 
  

Table 2:  Estimated size of tests on covariate parameters based on Cox’s and the
Lindley-cox models with 20% censored data.

Close

Table 2: Note: Values of${\stackrel{}{\stackrel{\wedge }{\alpha }}}_s=100\times T_s\text{.}/ms$(s=c,l), where Ts is the number of times the tests rejected H₀ out of m=5,000 replicates for different sample sizes with 20% censored data. Tests are run atα=0.05. I and II denote Likelihood ratio and Wald chi-square, respectively. CI=95% confidence interval.

Power of tests of hypotheses: The null parameter values used in assessing power are β₁=1.56, β₂=0.096, β₃=0.72, β₄=0.96, β₅=1.68, β₆=1.44, reflecting a 20% deviation from the original covariate parameter values. The results for power of tests of hypotheses for complete data are presented in Table 3, for comparison between Cox’s and Lindley-Cox for tests of the hypothesis that parameter vector is a specific value and for comparison between Cox’s and Lindley-Cox model for tests of the hypothesis that a component of parameter vector is a specific value. The results for assessing the power of tests of hypotheses for data with 20% censoring are presented in Table 4.

Table 3: Estimated Power of Tests on Covariate Parameters Based on Cox’s and the Lindley-Cox Models with Complete Data.

  

    
H0:b=b0+D 
  
  

    
 
    
Sample Size  
  
  

    
Model
    
25
    
50
    
100
    
250
    
500
    
1,000
  
  

    
 
  
  

    
L-Cox I
    
9.12
    
12.46
    
23.16
    
58.48
    
90.36
    
99.82
  
  

    
CI
    
8.32, 9.92
    
11.54, 13.38
    
21.19,24.33
    
57.11, 59.85
    
89.54, 91.16
    
99.70, 99.94
  
  

    
L-Cox II
    
13.17
    
15.00
    
25.18
    
59.78
    
90.52
    
99.89
  
  

    
CI
    
12.24, 14.14
    
14.01, 15.99
    
23.98, 26.38
    
58.42, 61.14
    
89.71,91,33
    
99.97,99.94
  
  

    
Cox I
    
14.24
    
11.86
    
16.48
    
36.52
    
66.70
    
94.40
  
  

    
CI
    
13.27, 15.21
    
10.96, 12.79
    
15.45, 17.51
    
35.19, 37.85
    
55.39, 68.01
    
93.76, 95.04
  
  

    
Cox II
    
13.44
    
13.68
    
18.42
    
38.66
    
68.16
    
94.78
  
  

    
CI
    
12.49, 14.39
    
12.73, 14.63
    
17.35, 19.52
    
37.31, 40.01
    
66.87, 69.45
    
94.16, 95.38
  
  

    
H0:b1=b01+D 
  
  

    
 
  
  

    
L-Cox I
    
6.79
    
8.36
    
14.26
    
31.94
    
57.72
    
87.76
  
  

    
CI
    
6.10, 7.49
    
7.59, 9.13
    
13.29, 15.23
    
30.65, 33.23
    
56.35, 59.09
    
86.85, 88.67
  
  

    
L-Cox II
    
7.90
    
10.20
    
15.74
    
33.86
    
59.30
    
88.22
  
  

    
CI
    
7.15, 8.65
    
9.36, 11.04
    
14.73, 16.75
    
32.55, 35.17
    
57.94, 60.66
    
87.33, 89.11
  
  

    
Cox I
    
9.64
    
8.18
    
10.18
    
24.98
    
47.22
    
79.66
  
  

    
CI
    
8.82, 10.46
    
7.42, 8.94
    
9.34, 11.02
    
23.78, 26.18
    
45.84, 48.60
    
78.54, 80.78
  
  

    
Cox I
    
9.42
    
9.22
    
11.74
    
26.78
    
48.44
    
80.42
  
  

    
CI
    
8.61, 10.23
    
8.42, 10.02
    
10.85, 12.63
    
25.55, 28.01
    
47.05, 49.83
    
79.32, 81.52
  

Table 3:  Estimated Power of Tests on Covariate Parameters Based on Cox’s
and the Lindley-Cox Models with Complete Data.

Close

Table 3:Note: Values of ${\stackrel{}{\stackrel{\wedge }{p}}}_s=100\times T_s\text{.}/ms$ (s=c,l), where Ts is the number of times the tests rejected H₀ out of m=5,000 replicates for different sample sizes with complete data. I and II denote Likelihood ratio and Wald chi-square, respectively. Δ denotes 20% of covariate parameters value. L-Cox=Lindley-Cox.

Table 4: Estimated Power of Tests on Covariate Parameters Based on Cox’s and the Lindley-Cox Models for 20% Censored data.

  

    
H0:b=b0+D 
  
  

    
 
    
Sample Size  
  
  

    
Model
    
25
    
50
    
100
    
250
    
500
    
1,000
  
  

    
 
  
  

    
L-Cox I
    
9.60
    
11.92
    
19.38
    
46.94
    
81.28
    
98.80
  
  

    
CI
    
8.78, 10.42
    
11.02, 12.82)
    
18.28, 20.48
    
45.56, 48.32
    
80.20, 82.36
    
98.50, 99.10
  
  

    
L-Cox II
    
12.31
    
14.20
    
21.02
    
48.12
    
81.72
    
98.82
  
  

    
CI
    
11.40, 13.23
    
13.23, 15.17
    
19.89, 22.15
    
46.74, 49.50
    
80.65, 82.78
    
98.52, 99.12
  
  

    
Cox I
    
13.84
    
11.42
    
14.16
    
28.78
    
54.64
    
88.94
  
  

    
CI
    
12.88, 14.80
    
10.54, 12.30
    
13.19, 15.13
    
27.53, 30.06
    
53.26, 56.02
    
88.07, 89.81
  
  

    
Cox II
    
11.30
    
12.86
    
16.06
    
31.18
    
56.36
    
89.58
  
  

    
CI
    
10.42, 12.18
    
11.93, 13.79
    
15.05, 17.11
    
29.90, 32.46
    
54.99, 57.73
    
88.73, 90.43
  
  

    
H0:b1=b01+D 
  
  

    
 
  
  

    
L-Cox I
    
7.09
    
8.92
    
12.08
    
26.16
    
48.42
    
78.54
  
  

    
CI
    
6.38, 7.81
    
8.13, 9.71
    
11.18, 12.98
    
24.94, 27.38
    
47.03, 49.81
    
77.40, 79.68
  
  

    
L-Cox II
    
8.31
    
10.42
    
13.90
    
28.30
    
49.98
    
79.10
  
  

    
CI
    
7.54, 9.08
    
9.57, 11.27
    
12.94, 14.86
    
27.05, 29.55
    
48.59, 51.37
    
77.97, 80.23
  
  

    
Cox I
    
10.22
    
8.38
    
9.44
    
20.76
    
40.00
    
69.46
  
  

    
CI
    
9.38, 11.06
    
7.61, 9.15
    
8.63, 10.25
    
19.64, 21.88
    
38.64, 41.36
    
68.18, 70.74
  
  

    
Cox II
    
8.78
    
9.18
    
10.64
    
22.14
    
41.38
    
70.46
  
  

    
CI
    
8.00, 9.56
    
8.38, 9.98
    
9.79, 11.49
    
20.99, 23.29
    
40.01, 42.75
    
69.20, 71.7
  

Table 4:  Estimated Power of Tests on Covariate Parameters Based on Cox’s
and the Lindley-Cox Models for 20% Censored data.

Close

Table 4: Note: Values of${\stackrel{}{\stackrel{\wedge }{p}}}_s=100\times T_s\text{.}/ms$(s=c ,l), where Ts is the number of times the tests rejected H₀ out of m=5,000 replicates for different sample sizes with 20% censored data. I and II denote Likelihood ratio and Wald chi-square, respectively. Δ is 20% deviation from parameter values. CI=95% confidence interval. L-Cox=Lindley-Cox.

Comments

Using simulation, this study assesed size and power of tests of hypotheses on parameters of the Lindley-Cox model arising from the maximum likelihood estimators (MLE) of those parameters, and compared the results of size and power of tests on β arising from Lindley-Cox MLE estimator with that arising from Cox’s partial maximum likelihood estimator.

The tests of the hypotheses H₀:β= β₀ and H₀:β₃= β₀₃ for complete and 20% censored data (Tables 1 & 2) are essentially a-level tests with the possible exception in small samples. Note that, for 20% censored data, the size of the Wald chi-square test for the global null hypothesis for the parameters from the Lindley-Cox model is estimated as 8.11% for n=25. This may be due to sample size being too small to rely on the Wald tests. Likelihood ratio test from the Cox’s PH for n=25 appears to have high false positive. Peace [5] and Peace [4] observed similar results. A possible explanation is that this sample size may be too small to warrant reliance on the asymptotic properties of the partial MLE estimator from the Cox’s model.

For power of tests of the hypotheses H₀:β= β₀+Δ and H₀:β₃= β₀₃+Δ , Cox PH appears to have comparable power as the Lindley- Cox when the data are complete or contain 20% censored data, with possible exceptions for some large samples, i.e., the cases n>100 where Lindley-Cox seems to have higher power (Table 3). Results based on using different values for the hazard function to simulate the censoring distribution are consistent with those presented.

Kalbfleisch [8], Peace [5], Efron [9], and Peace [4] demonstrated the robustness of inference on the covariate parameters from the Cox PH model and the method of estimation to inference on covariate parameters using the full maximum likelihood method when specifying the time-dependent component of the hazard to be constant (exponential distribution), power law (Weibull distribution) and exponential law (Gompertz distribution). The comparability of the results for size and power assessment of tests on the covariate parameters comparing inference from the Cox PH model with that from the Lindley-Cox Model is yet another example of the robustness of the Cox PH model to specific functional forms of the timedependent component of the hazard function.

Conclusion

Results of this study suggest that size of tests of hypotheses on parameters arising from the maximum likelihood estimator of parameters in the Lindley-Cox model are a-level tests for complete data and 20% censored data for the hypotheses H₀:β= β₀ and H₀:β₁= β₀₁. Additionally, the power of tests of hypotheses H₀:β= β₀+Δ and H₀:β₁= β₀₁+Δ, where represents a 20% deviation in respective parameter values on parameters arising from partial maximum likelihood estimation of the covariate parameters from the Cox’s model are lower for large samples than those arising from maximum likelihood estimation of the covariate parameters in the Lindley-Cox model.

Real Data Applications

Illustration 1: Freireich et al. [3] provides survival times in weeks for terminally ill cancer patients. Survival times in weeks of the 21 untreated patients were 1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15, 17, 22 and 23. Kleinbaum and Klein [15] presents detailed analyses of the same data set in relation to covariate information, notably the log of White Blood Cell (WBC) count. We fit the Lindley-Cox model to the data set for untreated patients to assess whether the WBC is correlated with survival times.

Estimated coefficients for assessment of correlation between survival times and log WBC using different models are presented in Table 5. The parameter estimates from the models are consistent with the log WBC count been associated with survival times. The Linldey- Cox appears to show a better fit as suggested by smaller Akaike Information Criteria (AIC) [22] and Bayesian Information Criteria (BIC) [23] (Table 5). These model comparison approaches enable contrast of non-nested models using log-likelihood but penalize for model complexity.

Table 5: Estimated Coefficient for Correlation Assessments for the Freireich et al. (1963) Data using the Peace’s Negative Exponential and Lindley-Cox Models.

  

    
Parameters
    
Peace
    
Lindley-Cox
    
Cox
  
  

    
 
  
  

    
�(SE)
    
0.0143 (0.01253)
    
0.02144 (0.0112)
    
-
  
  

    
 
  
  

    
�(SE)
    
0.6967 (0.2631)
    
1.264 (0.307)
    
1.2807 (0.40054)
  
  

    
 
  
  

    
BIC
    
132.1
    
121.7
    
-
  
  

    
AIC
    
130.0
    
119.6
    
-
  
  

    
Note: -2 log likelihood, AIC, and BIC were provided for only    Parametric models whose estimates are based full maximum likelihood    estimator.
      
 
  

Table 5:  Estimated Coefficient for Correlation Assessments for the Freireich et
al. (1963) Data using the Peace’s Negative Exponential and Lindley-Cox Models.

Close

Figure 1 presents the observe and expected survival probabilities; the plot suggests that the Lindley-Cox survival probabilities approximates well that of the observed (Kaplan-Meier). A chi-square goodness of fit test based on the intervals (0,5],(5,10],(10,15],(15,23) failed to reject the null hypothesis that the Lindley-Cox density provides a good fit to the data $({\chi }_3^2=1.678;p=0.6418)$ .

Figure 1: Survival Probabilities for the Freireich et al. (1963) Data.

    

    

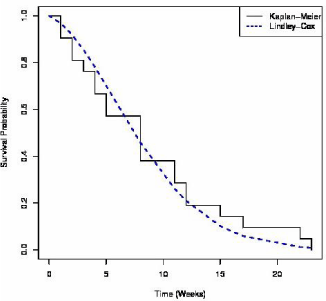
    Figure 1:  Survival Probabilities for the Freireich et al. (1963) Data.
    
    

Close

Acknowledgment

The authors thank Kao-Tai Tsai, Broderick Oluyede, and Lili Yu for reviewing some of the software programs and for their comments.

References

1. Lindley DV. Fiducial distributions and Bayes’ Theorem. Journal of the Royal Statistical Society. 1958; 20: 102-107.
2. Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and its application. Mathematics and Computers in Simulation. 2008; 78: 493-506.
3. Freireich EO, Gehan E, Frei E, Schroeder LR, Wolman IJ, Anbari R, et al. The effect of 6-mercaptopmine on the duration of steroid induced remission in acute leukemia: "a model for evaluation of of other potentially useful therapy". Blood. 1963; 21: 699-716.
4. Peace K, Flora R. Size and power assessment of tests of hypotheses on survival parametrs. Journal of the American Statistical Association. 1978; 73: 129-132.
5. Peace K. Maximum likelihood estimation and efficiency assessments of tests of hypotheses on survival parameters [PhD Dissertation]. Medical College of Virginia, Virginia Commonwealth University. Richmond, Virginia. 1976.
6. Mehrotra DV, Roth AJ. Relative risk estimation and inference using a generalized logrank statistic.Stat Med. 2001; 20: 2099-2113.
7. Cox DR. Regression models and life-tables. Journal of the Royal Statistical Society. 1972; 34: 187–220.
8. Kalbfleisch JD. Some efficiency calculations for survival distributions. Biometrika. 1974; 61: 31–38.
9. Efron B. The efficiency of Cox’s Likelihood function for censored Data. Journal of the American Statistical Association. 1977; 72: 557-565.
10. Feigl P, Zelen M. Estimation of exponential survival probabilities with concomitant information. Biometrics. 1965; 21: 826-838.
11. Zippin C, Armitage P. Use of concomitant variables and incomplete survival information in the estimation of an exponential survival parameter. Biometrics. 1966; 22: 665–672.
12. Glasser MN. Exponential survival with covariates. Journal of the American Statistical Association. 1967; 62: 561-568.
13. Sprott DA, Kalbfeisch JD. Examples of likelihoods and comparison with point estimates and large sample approximations. Journal of the American Statistical Society. 1969; 64: 468-484.
14. Breslow NE. Covariance analysis of censored survival Data. Biometrics. 1972; 3: 80-99.
15. Prentice RL. Exponential survival with censoring and explanatory variables. Biometrika. 1973; 60: 279- 288.
16. Therneau TM, Grambsch PM. Modeling Survival Data: Extending the Cox Model. Springer. 2010; 12.
17. Bender R, Augustin T, Blettner M . Generating survival times to simulate Cox proportional hazards models by Ralf Bender, Thomas Augustin and Maria Blettner, Statistics in Medicine 2005; 24:1713-1723. Stat Med. 2006; 25: 1978-1979.
18. Qian J, Li J, Chen P. Generating survival data in the simulation studies of Cox’s model. Proceedings of Information and Computing, 2010 Third International Conference, Wuxi, Jiang Su; IEEE Computer Society Washington. 2010; 4: 93-96.
19. Okwuokenye M. Size and power assessment of tests of hypotheses on parameters when modeling time-to-event data with Lindley distribution [Doctoral Dissertation]. Jiang Ping-Hsu College of Public Health, Georgia Southern University. Statesboro, Georgia. 2012.
20. Okwuokenye M, Peace KE. A Comparison of Size and Power of Tests of Hypotheses on Parameters Based on Two Generalized Lindley Distributions. Communications for Statistical Applications and Methods. 2015; In Press.
21. Kleinbaum DG, Klein M. Survival Analysis: A Self-Learning Text. Springer. 2005.
22. Akaike H. A new look at the statistical model identification. IEEE transaction on Automatic control. 1974; 19: 716-723.
23. Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978; 6: 461-464.

Download PDF

Citation: Okwuokenye M and Peace KE. Size and Power of Tests of Hypotheses on Survival Parameters from the Lindley Distribution with Covariates. Austin Biom and Biostat. 2015;2(4): 1026. ISSN: 2378-9840

Home

Journal Scope

Online First

Current Issue

Editorial Board

Instruction for Authors

Submit Your Article

Contact Us