A Relative Agreement Model for Simulating Human Decision Making and Preventive Behavior during Epidemics

Research Article

Austin J Infect Dis. 2014;1(3): 7.

A Relative Agreement Model for Simulating Human Decision Making and Preventive Behavior during Epidemics

Liang Mao*

Department of Geography, University of Florida, USA

*Corresponding author: Liang Mao, Department of Geography, University of Florida, 3141 Turlington Hall, Gainesville, Florida, USA

Received: August 25, 2014; Accepted: October 25, 2014; Published: October 27, 2014

Abstract

Many computational and mathematic models have been developed to understand human preventive behaviors against infectious diseases and suggest intervention policies. A majority of these models have paid attention to behavioral changes between epidemics, but those occurring within a single epidemic should not be ignored. This article proposes a disease-behavior model with a focus on short-term human decision making process during an epidemic and the resultant adoption of preventive behaviors. Based on relative-agreement rules, this model explicitly represents discrete individuals, the social interactions between individuals, their responses to disease risks, and most importantly, the individualized decision making process. The simulation results suggest that a seasonal influenza epidemic can be controlled by voluntary preventive behavior if above 60% of the population initially held positive attitude toward the adoption. This threshold percentage would elevate as the transmissibility of influenza increases, but can also be reduced by improving the efficacy of preventive behaviors or by encouraging communications between individuals. A number of preventive strategies are recommended to deal with the current circumstances that new vaccines are often insufficient to combat emerging infectious diseases.

Keywords: Preventive behavior; Infectious diseases; Agent-based modeling; Relative agreement rules; Social network

Introduction

Recent outbreaks of emerging communicable diseases, such as the new H1N1 flu in 2009 and Ebola in 2014, have attracted substantial interests in understanding human responsive behavior against diseases, from which practical intervention policies could be suggested [1,2]. Since effective vaccines require sufficient time to develop and manufacture, the best human response at early stage of epidemics is to adopt preventive behaviors, for example, wearing facemasks, performing hand hygiene, taking antiviral drugs, and avoiding close contact with people with symptoms of active infections [3]. Knowledge on the drivers and decision processes toward adopting these preventive behaviors is critical to early control and prevention of outbreaks.

Many computational and mathematical models have been developed to deepen our knowledge on this topic [4-6]. Due to complexity of human-disease systems, challenges in modeling concern not only how to model human responses to the presence of epidemics, but also how these responses affect the spread of the disease itself [7-9]. To date, only a small number of models have been developed to account for interactive mechanisms between diseases and human responsive behavior, with a majority of them being focused on vaccinations[4, 5, 10]. These existing models take a long-term view on seasonal disease outbreaks over years, and assume that individuals only make decision to adopt preventive behavior before each epidemic season, while doing nothing during an epidemic. This is not always the truth, because many individuals may be aware of disease risks during a single epidemic and then react before the epidemic ends. Little attention so far has been paid to modeling human voluntary preventive behaviors within an epidemic.

This article aims to address this knowledge gap by developing a disease-behavior model with relative agreement decision rules. The model focuses on short-term human decision making processes within an epidemic and the resultant adoption of preventive behavior. Using this model, a sensitivity analysis is conducted to explore potential strategies that could promote preventive behaviors among the population and help control epidemics. The remainder of this article describes the construction of disease-behavior model and its parameterization, discusses simulation outcomes, and the resulting implications.

Methodology Design

Conceptual model and assumptions

From a modeling perspective, both the transmission of diseases and the adoption of preventive behaviors can be conceptualized as diffusion processes. The disease spreads from individual to individual through their physical contacts, while the preventive behaviors disperse through the "word-of-mouth" discussion [11-13]. These two diffusion processes run simultaneously and interact with one another. Individuals being infected may adopt preventive behaviors themselves, and further motivate others to adopt. Conversely, the adoption of preventive behaviors limits the transmission of influenza by protecting individuals from infection. The disease-behavior diffusion model is established based on six assumptions:

  1. Individuals in a population are linked together by a social network. Individuals have contact with one another through the network.
  2. Every individual has a property of infection status, which can be susceptible, latent, infectious or recovered [14,15]. The contact between individuals through the social network triggers the change of infection status, which follows the natural history of the disease.
  3. Each individual also holds an attitude toward the preventive behaviors, which can be positive, neutral, or negative. The initial attitude is a mixed product of the individual's knowledge, experiences, perceived barriers and benefits [16]. The attitude may evolve over time due to interpersonal influences, and finally determine whether to adopt preventive behaviors or not.
  4. During a disease epidemic, individuals discuss with their contacts about the adoption issue, which in turn influences their attitude with one another. The discussion between individuals drives the diffusion of preventive behaviors throughout the population.
  5. The adoption of preventive behaviors can reduce the transmissibility of a disease to different degrees, depending on infection status of individuals.
  6. The manifestation of disease symptoms will change an individual's attitude positively toward the adoption of preventive behaviors.

To build a working simulation model, each of these six assumptions is formulated and then programmed. Following steps illustrate the formulation design in a hypothetic population.

Step 1: Modeling the social network (Assumption 1): A hypothetic social network of 5,000 individuals is modeled for simulation. Each individual is assumed to have contact with 12 other individuals, including two family members and ten workplace colleagues. This total number of contacts (links) per individual is based on the average size of a typical American family and workplace[17,18]. Individuals are mixed into a 'small-world' network structure [19], i.e., an individual can be connected to any other individual through a few links (a short path length), and meanwhile the direct contacts of this individual are also directly linked with one another (a high degree of interconnection). The short path length facilitates the long-range diffusion, while the high degree of interconnection supports the local diffusion. Following the classic algorithm proposed by Watts [20], this "small-world" structure is generated by assigning a majority of links (95%) between individuals based on proximity, while the other links (5%) randomly among individuals.

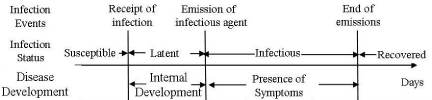
Step 2: Modeling the diffusion of diseases (Assumption 2): Influenza is taken as a typical example of infectious diseases, and its diffusion is simulated by varying the infection status of every individual over time. As shown in Figure 1, once having contact with an infectious individual, a susceptible individual may be infected with the influenza virus and enter into the latent status. The likelihood of infection is specified as a probability referred to as the transmission rate (r), based on which the Monte-Carlo method can be applied to simulate the transmission or not. The infection starts a latent period, during which influenza develops internally and cannot be transmitted. The end of latent period moves the individual into an infectious status and enables the individual to transmit influenza virus to other susceptible contacts. During the infectious period, the individual may develop symptoms of influenza or remain asymptomatic. At the end of the infectious period, the individual recovers, and develops immunity in the remaining period of an epidemic. The diffusion of influenza can be then implemented by tracking susceptible contacts of infectious individuals every simulation day and emulating the transmission between them with the Monte-Carlo method.

Figure 1: The infection events and status in the natural history of influenza.






Figure 1:  The infection events and status in the natural history of influenza.

Step 3: Modeling the diffusion of preventive behaviors (Assumption 3&4): In behavioral science, the diffusion of a behavior in a population can be modeled as gradual variations of individuals' attitudes toward adoption [13,21,22]. Following steps depict the formulation of individuals' attitude on adoption, their decision process, and the interchange of individuals' attitudes through discussion.

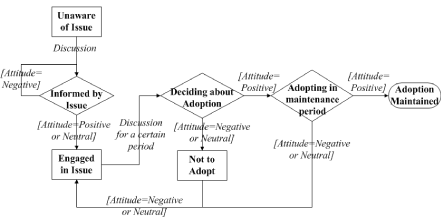
Step 3.1: Decision process toward adoption: The human decision making is formulated as a staged process, following the concept of Precaution Adoption Process Model (PAPM) [23,24]. As shown in Figure 2, an individual starts with an Unaware status of the preventive behaviors. At some time point, this individual may be Informed about the behaviors through discussion with contacts. Once informed, this individual develops an initial attitude (positive, neutral or negative) toward the adoption. If the initial attitude is positive or neutral, this individual is willing to further discuss this issue with others (Engaged). Otherwise, this individual will disregard this issue (staying at Informed). After engaging in discussion for a certain period (the discussion period tc), this individual moves into a decision status (Deciding about Adoption). The decision making finally leads to one of three results according to the current attitude: Adopting if holding a positive attitude, or Not to Adopt if holding a negative attitude, or return to the Engaged stage for further discussion if holding a neutral attitude. At the Adopting stage, if an individual can keep the positive attitude for a certain period (the maintenance period tm), then the adoption is Maintained; otherwise, the individual will give up the adoption during the maintenance period.

Figure 2: The staged process of an individual to adopt the preventive behaviors. The squares and diamonds represent adoption stages. The comments on arrows describe the conditions for transition.






Figure 2:  The staged process of an individual to adopt the preventive behaviors. The squares and diamonds represent adoption stages. The comments on arrows describe the conditions for transition.

Individuals' attitude toward adoption is formulated by introducing a concept of attitude segment, as an individual property, from previous work by Deffuant et al. [25]. The attitude segment of individual i is defined as a mathematic range within ai ± uai, where ai is the attitude value and uai is the associated uncertainty. The attitude value (ai) is a negative or positive real number, initially drawn from a normal distribution N (m, σ). The associated uncertainty (uai) is a real number that represents a mix between individual i's uncertainty, conviction, and openness to the attitudes of others. For simplicity, it is initialized with a same value for every individual.

Turning back to Figure 2, if ai - uai>0, individual i is positive toward adoption. If ai + uai <0, individual i has a negative attitude. Otherwise (ai + uai ≥0 and ai - uai≤0), individual i is neutral [25]. Individuals' attitude values vary over time by discussions with social contacts, and as a result, the staged decision process is propelled.

Step 3.2: Discussion between individuals: Corresponding to Assumption 4, once an individual has contact with another, there is a probability γ that they will discuss the adoption issue. During the discussion, an individual's attitude will be influenced by others following rules of "relative agreement" [25]. These rules assume that: 1) the attitude segment with low uncertainty (e.g., strong minded people) are more influential than that with high uncertainty; 2) the more the overlap between attitude segments, the more likely that the individuals may influence one another; 3) when the overlap between two attitude segments is too small, there is no influence. These "relative agreement rules" are formulated as follows:

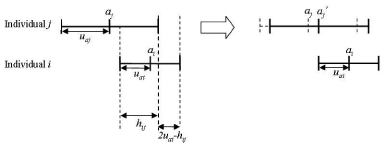
Given that individual i has an attitude segment ai ±uai, the influence of individual i on individual j, when they discuss, is determined by their agreement, i.e., the overlap section (hij) of the two individuals' attitude segments minus the non-overlap section (2uoi-hij) (Equation 1 and illustration in Figure 3).

Figure 3: The influence of individual i on individual j based on the "relative agreement rules" proposed by Deffuant et al [25].






Figure 3:  The influence of individual i on individual j based on the "relative agreement rules" proposed by Deffuant et al [25].

Agreement= hij-(2uai-hij)=2(hij- uai)

Where, hij=|min(ai+ uai,aj+uaj)-max(ai-uai,aj-uaj)||

Then, the relative agreement between i and j is calculated by the agreement divided by the total range of i's attitude segment 2uai:

2( h ij − u ai ) 2 u ai = h ij u i −1       ( 2 ) MathType@MTEF@5@5@+=feaaguart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaalaaabaGaaGOmaiaacIcacaWGObWaaSbaaSqaaiaadMgacaWGQbaabeaakiabgkHiTiaadwhadaWgaaWcbaGaamyyaiaadMgaaeqaaOGaaiykaaqaaiaaikdacaWG1bWaaSbaaSqaaiaadggacaWGPbaabeaaaaGccqGH9aqpdaWcaaqaaiaadIgadaWgaaWcbaGaamyAaiaadQgaaeqaaaGcbaGaamyDamaaBaaaleaacaWGPbaabeaaaaGccqGHsislcaaIXaGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcGaaiiOamaabmaabaGaaeOmaaGaayjkaiaawMcaaaaa@54D4@

If hij> ui (the relative agreement>0), then the modifications of aj and uaj by the interaction with i are updated as Equation 3:

a j = a j +( h ij u i −1)( a i − a j ) MathType@MTEF@5@5@+=feaaguart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadggadaWgaaWcbaGaamOAaaqabaGccqGH9aqpcaWGHbWaaSbaaSqaaiaadQgaaeqaaOGaey4kaSIaaiikamaalaaabaGaamiAamaaBaaaleaacaWGPbGaamOAaaqabaaakeaacaWG1bWaaSbaaSqaaiaadMgaaeqaaaaakiabgkHiTiaaigdacaGGPaGaaiikaiaadggadaWgaaWcbaGaamyAaaqabaGccqGHsislcaWGHbWaaSbaaSqaaiaadQgaaeqaaOGaaiykaaaa@4A70@ u aj = u aj +( h ij u ai −1)( u ai − u aj )                  ( 3 ) MathType@MTEF@5@5@+=feaaguart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadwhadaWgaaWcbaGaamyyaiaadQgaaeqaaOGaeyypa0JaamyDamaaBaaaleaacaWGHbGaamOAaaqabaGccqGHRaWkcaGGOaWaaSaaaeaacaWGObWaaSbaaSqaaiaadMgacaWGQbaabeaaaOqaaiaadwhadaWgaaWcbaGaamyyaiaadMgaaeqaaaaakiabgkHiTiaaigdacaGGPaGaaiikaiaadwhadaWgaaWcbaGaamyyaiaadMgaaeqaaOGaeyOeI0IaamyDamaaBaaaleaacaWGHbGaamOAaaqabaGccaGGPaGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcGaaiiOaiaacckacaGGGcWaaeWaaeaacaqGZaaacaGLOaGaayzkaaaaaa@6605@

By varying individuals' attitudes according to their social network and these formulated interaction rules, the model emulates the decision making process (Figure 2) for every individual. As a result, the variation of individuals' adoption status collectively leads to the diffusion of preventive behaviors over the population.

Step 4: Interactions between the two diffusion processes (Assumption 5&6):

Previous three steps have formulated the two diffusion processes independently, and the last step is to model their interactions. For model simplicity, the interactions are formulated into two factors corresponding to Assumption 5 and 6, namely, the efficacy of preventive behaviors (p) and the change of attitude by infection (q). Specifically:

  1. If Individual i is susceptible, the adoption of preventive behaviors can reduce the probability of being infected by p%;
  2. If Individual i is in the latent status, the adoption can reduce the probability of becoming infectious by p%/2;
  3. If Individual i is already infectious, the adoption may reduce the probability of infecting others by p%/2;
  4. Once Individual i is symptomatic, the attitude value ai will increase by q% of the uncertainty uai, i.e., ai +q%• uai; Further, if Individual j has discussed with i, the attitude value will increase by q%/2 of associated uncertainty uaj, i.e., aj +q%• uaj/2;

Upon the completion of the four steps described above, a disease-behavior (dual) diffusion model is established. This model is then parameterized for simulation and sensitivity analysis.

Model parameterization for simulation

Based on a pilot study and the literature, Table 1 specifies a default setting for model parameters during the simulation [24- 28]. This default setting produces a population with approximately equal proportions of individuals with positive, neutral and negative attitude at the start of the simulation, hereinafter referred to as initially positive, neutral and negative individuals, respectively. The transmissibility of influenza is set to be close to a moderate seasonal influenza [28, 29].

Table 1: The default disease-behavior scenario for model simulation.




  

    
Components Parameters 

    
Values 

  

  

    
Social    Network

    
Population size

    
5000

  

  

    
Average number of contacts of    an individual

    
12

  

  

    
Average path length

    
5.1

  

  

    
Clustering coefficient

    
0.7

  

  

    
Influenza

    
Transmission rate (r)

    
0.1

  

  

    
Latent period (tl)

    
1 day

  

  

    
Infectious period (ti)

    
4 days

  

  

    
Preventive    Behaviors

    
Mean of initial attitude    distribution (m)

    
0

  

  

    
Standard deviation of initial    attitude distribution (s)

    
0.1

  

  

    
Initial uncertainty of    individuals' attitude (ua)

    
0.05

  

  

    
Probability of discussion (γ)

    
0.25

  

  

    
Discussion period (tc)

    
1 day

  

  

    
Maintenance period (tm)

    
1 day

  

  

    
Interaction

    
Efficacy of preventive    behaviors on infection (p)

    
60%

  

  

    
Change of attitude by infection    (q)

    
50%

  









Table 1:  The default disease-behavior scenario for model simulation.

All individuals are initially assigned susceptible and unaware of the adoption. At the first day of simulation, one individual is randomly selected to become infectious to initialize the diffusion of influenza. Meanwhile, another individual is randomly selected to become informed to initialize the diffusion of preventive behaviors. The simulation of both diffusion processes takes a daily time step over 120 days.

Scenario and sensitivity analysis

As model outcomes, the diffusion of influenza is described by an epidemic curve that depicts the percent of infection in the population through the course of the epidemic. The diffusion of preventive behaviors is described by an adoption curve that depicts the percent of adoption in the population during the diffusion. In addition, the evolution of individuals' attitudes is also displayed by plotting respective proportions of positive, neutral and negative individuals in the population during the diffusion.

This research first compares how one of the two processes diffuses with and without the other. In other words, the dual-diffusion scenario (from the default parameter settings) is compared to an adoption-only scenario (no disease epidemic: transmission rate r =0), and to an influenza-only scenario (no spread of preventive behavior: the probability of discussion γ =0). For each of the three scenarios, the average value of 100 realizations is used to construct the epidemic curve, adoption curve, and the attitude evolution curves.

Furthermore, a sensitivity analysis is conducted to explore effective strategies to control influenza epidemics. In particular, this research is interested in the minimum proportion of initially positive individuals required to control an epidemic by voluntary preventive behavior. The proportion of initially positive individuals in the population, denoted as β0, is varied from 0 to 100% by increasing the mean of initial attitude distribution (m). The parameter β0 is paired with four other parameters respectively in the sensitivity analysis, including: 1) the transmission rate of influenza r (from 0 to 0.2); 2) the efficacy of preventive behaviors on infection p (from 0 to 100%); 3) the infection-related change in attitude q (from 0 to 100%); and 4) the probability of discussion γ (from 0 to 1). Each pair of parameters is given alternative values while holding all other parameters as default (Table 1). For a given pair of parameter values, 100 model realizations are performed to estimate the percent of infection in the population. The epidemic is assumed to be controlled if the resultant percent of infection is less than 10% of the population.

Simulation Results and Discussion

Scenario analysis

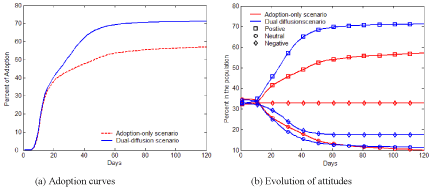
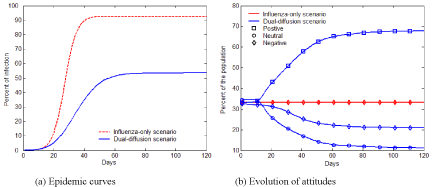
Figure 4 compares the diffusion of preventive behaviors with and without an influenza epidemic. For the adoption-only scenario (influenza transmission rate r=0), the adoption curve starts with an abrupt rise during the first 20 days, and then increases slowly till the last day (the red dashed line in Figure 4a). Approximately 50% of the population would adopt the preventive behaviors. The early abrupt rise can be attributed to the initially positive individuals, who are informed by discussion and quickly adopt the preventive behaviors. The later slow increase could be explained as a number of initially neutral individuals changing their attitudes to positive after discussions, and finally adopting the preventive behaviors (the red curve with circles in Figure 4b). Compared to the adoption-only scenario, adding the diffusion of influenza causes a marked increase in adopters (the blue solid line in Figure 4a). The total number of adopters has the same rise as the adoption-only scenario before Day 20, but remains a fast increase from Day 20 to 60. This later fast increase is because a number of negative individuals change to positive attitudes due to infection (the blue curve with diamonds in Figure 4b). More individuals, therefore, finally adopt the preventive behaviors and the percent of adoption reaches a higher level (about 70% of the population).

Figure 4: The comparison of the dual-diffusion scenario (blue) to the adoptiononly scenario (red). (a) The adoption curves depict the percent of adoption in the population over time. The solid line represents the dual-diffusion scenario (transmission rate r=0.1), while the dash line represents the adoption-only scenario with r=0. (b) The evolution of the proportion of positive (square), neutral (circle) and negative (diamond) individuals in the population over time.






Figure 4:  The comparison of the dual-diffusion cenario (blue) to the adoptiononly scenario (red). (a) The adoption curves depict the percent of adoption in the population over time. The solid line represents the dual-diffusion scenario (transmission rate r=0.1), while the dash line represents the adoption-only scenario with r=0. (b) The evolution of the proportion of positive (square), neutral (circle) and negative (diamond) individuals in the population over time.

Figure 5 illustrates the difference between the spread of influenza with and without the diffusion of preventive behaviors. For the influenza-only scenario (the probability of discussion γ =0), influenza can infect nearly entire population within 30 days (the red dash line in Figure 5a). Due to the lack of discussion, individuals are unaware of the preventive behavior, and no one starts the decision making process toward adoption (the flat red curves in Figure 5b). Once the diffusion of preventive behaviors is added (γ =0.25), the transmission of influenza can be significantly slowed with only half of the population being infected (the blue solid line in Figure 5a). Through discussion, an increasing number of individuals are gradually aware of the adoption issue, change their attitude to positive, and decide to adopt preventive behaviors, which reduce the transmissibility of influenza (See the blue curves in Figure 5b).

Figure 5: The comparison of the dual-diffusion scenario (blue) to the influenzaonly scenario (Red). The epidemic curves depict the percent of infection in the population over time. The solid line represents the dual-diffusion scenario (discussion probability γ =0.25), while the dash line represents the influenzaonly scenario with γ =0. (b) The evolution of the proportion of positive (square), neutral (circle) and negative (diamond) individuals in the population over time.






Figure 5:  The comparison of the dual-diffusion scenario (blue) to the influenzaonly scenario (Red). The epidemic curves depict the percent of infection in the population over time. The solid line represents the dual-diffusion scenario (discussion probability γ =0.25), while the dash line represents the influenzaonly scenario with γ =0. (b) The evolution of the proportion of positive (square), neutral (circle) and negative (diamond) individuals in the population over time.

Sensitivity analysis

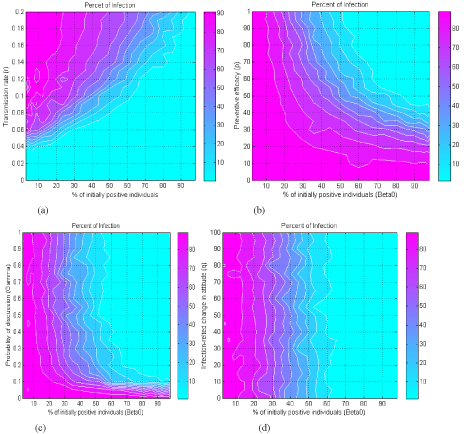
The model is further used to explore the minimum value of β0 (the proportion of initially positive individuals in the population) needed to control influenza epidemic by voluntary preventive behavior. Figure 6a displays the percent of infection as as a function of β0 and the transmission rate (r). For any given value of r, there exists a critical value for β0 to reduce the percent of infection under 10% (the cyan colored area in Figure 6a). The greater the transmission rate r, the higher the threshold value for β0 will be required. For a moderately transmissible influenza (r =0.1), e.g., the seasonal influenza, the epidemic can be controlled if at least 60% of the population initially holds positive attitude (β0 ≥ 60%). For a highly transmissible strain of influenza (r =0.2), e.g., the 1918 pandemic strain [30], the threshold value for β0 needs be raised to nearly 95% of the population to control the epidemic.

Figure 6: The percent of infection (represented by color ramp) as a function of the proportion of initially positive individuals (β0) and a) the transmission rate (r), b) the efficacy of preventive behaviors (p), c) the probability of discussion (γ), and d) the change of attitude by infection (q). The full cyan area indicates that the percent of infection is under 10%, and the influenza epidemic is controlled.






Figure 6:  The percent of infection (represented by color ramp) as a function of the proportion of initially positive individuals (β0) and a) the transmission rate (r), b) the efficacy of preventive behaviors (p), c) the probability of discussion (γ), and d) the change of attitude by infection (q). The full cyan area indicates that the percent of infection is under 10%, and the influenza epidemic is controlled.

Figure 6b shows how the preventive efficacy (p) interacts with the β0 to control epidemics. Given the value of p around 60%, e.g., the efficacy of taking anti-viral drugs [28], β0 must be greater than 70% of the population to achieve a successful control. Once the value of p can be improved to 90% (for example, anti-viral drugs + facemask), a critical value of 50% for β0 is sufficient for a successful control. A higher preventive efficacy can inhibit the transmission of influenza more effectively, and hence a small number of initially positive individuals are required. These results suggest an incentive program that offers individuals free facemasks or hand sanitizers if they buy anti-viral drugs in pharmacies. This multi-prevention strategy could be practical and effective in influenza control, because it not only improves the efficacy of prevention, but also motivates the adoption of preventive behaviors.

Another parameter that impacts epidemics is the probability of discussion between individuals (γ). Figure 6c shows that a 10% chance of discussion between individuals (γ=0.1) is the minimum requirement to control an influenza epidemic. Given that all individuals are initially unaware of the adoption issue, they need to be gradually informed to start their adoption processes. With a 10% chance of discussion, β0 must be greater than 90% (almost all individuals) to control the epidemics. If the probability of discussion can be raised to 0.5, the β0 only needs to reach 50% for a successful control. A higher probability of discussion means that individuals can be informed faster and make earlier decision toward adoption. These early adopters could timely limit the transmission of influenza and thus reduces the incidence of infection. This result suggests the importance of encouraging individuals to discuss the adoption issue. A propagation strategy can be designed to attract public attention onto the adoption issue through mass media, such as television, newspapers, and the internet.

Interestingly, Figure 6d indicates that the change of attitude by infection (q) is independent of the infection rate. Given any fixed β0, the percent of infection remain almost constant as q increases from 0 to 100%. This implies that even if an individual can make a 'big-turn' in attitude after infection and decide to adopt immediately, the influenza epidemic still cannot be controlled. The possible reason is that both the influenza and preventive behaviors diffuse on the same social network. When an individual is infected, the contacts of this individual might also be infected at the same time or even before. Although they may change their attitudes and adopt preventive behaviors, their infection status cannot change. The result could be more realistic if the infection network for disease diffusion and the communication network for behavior diffusion are modeled separately.

Still in its infancy, the presented model is so far a crude approximation of reality. The indirect contacts between individuals through telecommunications and the internet are not considered, which may play an important role in the diffusion of preventive behaviors. The role of mass media in informing people has not been modeled in this research, but can be taken into account in the future by setting a broadcasting rate among the population. Furthermore, the uncertainties in some model parameters may also affect the model results, such as the structure of social network and the initial distribution of individuals' attitude. The compensation for these limitations can improve the model accuracy, but also increase the complexity. It is argued that the goal of modeling is not to look for exactly what may happen, but rather for differences in outcomes between different scenarios [31]. In this sense, the proposed model framework could be a valuable prototype to guide the design of more realistic working models.

Conclusion

In this paper, an original simulation model has been proposed to couple the disease transmission and voluntary preventive behaviors against the disease. Based on the relative-agreement rules, this model explicitly represents discrete individuals, the social network between individuals, their responses to disease risks, and most importantly, their decision making processes. This model allows disease transmission to alter individuals' decision making, which in turn affects disease transmission. The comparison study show that any model that fails to account for this interaction mechanism could not accurately portray a realistic epidemic.

Using the proposed model, this research also explored the lower threshold of initially positive individuals to control influenza epidemics solely by voluntary preventive behavior. For disease control, it is not practical to have all individuals holding positive attitude toward adoption at the beginning of an epidemic. Many individuals may be reluctant to adopt preventive behaviors because of their knowledge, prior experience, incomes, occupations, and other factors [32,33]. The sensitivity analysis estimates that about 60% of the population with an initial positive attitude is necessary to successfully control a moderately transmissible influenza. This threshold would elevate as the transmissibility of influenza increases, but can also be reduced by improving the efficacy of preventive behaviors or by encouraging discussions between individuals. These results suggest a number of effective strategies to control influenza epidemics, such as the combination sale of anti-viral drugs and facemasks and the use of mass media to propagate adoption issues.

References

  1. Perisic A, Bauch CT. Social contact networks and disease eradicability under voluntary vaccination. PLoS Comput Biol. 2009; 5: e1000280.
  2. Funk S, Salathé M, Jansen VA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interface. 2010; 7: 1247-1256.
  3. National Center for Immunization and Respiratory Diseases, CDC; Centers for Disease Control and Prevention (CDC). Use of influenza A (H1N1) 2009 monovalent vaccine: recommendations of the Advisory Committee on Immunization Practices (ACIP), 2009. MMWR Recomm Rep. 2009; 58: 1-8.
  4. Vardavas R, Breban R, Blower S. Can influenza epidemics be prevented by voluntary vaccination? PLoS Comput Biol. 2007; 3: e85.
  5. Galvani AP, Reluga TC, Chapman GB. Long-standing influenza vaccination policy is in accord with individual self-interest but not with the utilitarian optimum. Proc Natl Acad Sci U S A. 2007; 104: 5692-5697.
  6. Wang B, Cao L, Suzuki H, Aihara K. Safety-information-driven human mobility patterns with metapopulation epidemic dynamics. Sci Rep. 2012; 2: 887.
  7. Sahneh FD, Chowdhury FN, Scoglio CM. On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading. Sci Rep. 2012; 2: 632.
  8. Fenichel EP, Castillo-Chavez C, Ceddia MG, Chowell G, Parra PA, Hickling GJ, et al. Adaptive human behavior in epidemiological models. Proc Natl Acad Sci U S A. 2011; 108: 6306-6311.
  9. Meloni S, Perra N, Arenas A, Gómez S, Moreno Y, Vespignani A. Modeling human mobility responses to the large-scale spreading of infectious diseases. Sci Rep. 2011; 1: 62.
  10. Zhang HF, Wu ZX, Tang M, Lai YC. Effects of behavioral response and vaccination policy on epidemic spreading--an approach based on evolutionary-game dynamics. Sci Rep. 2014; 4: 5666.
  11. Cliff AD. Spatial Diffusion: An Historical Geography of Epidemics in an Island Community: Cambridge University Press. 1981.
  12. Shannon GW, Bashshur RL, Metzner CA. The spatial diffusion of an innovative health care plan. J Health Soc Behav. 1971; 12: 216-226.
  13. Hägerstrand T. Innovation diffusion as a spatial process. Chicago: University of Chicago Press. 1967.
  14. Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. New York: Oxford University Press. 1992.
  15. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proceedings Royal Statistics Society. 1927; 115: 700-721.
  16. Glanz K, Rimer BK, Lewis FM. Health Behavior and Health Education: Theory, Research, and Practice. 3rd edn. San Francisco: Jossey-Bass. 2002.
  17. Edmunds WJ, O'Callaghan CJ, Nokes DJ. Who mixes with whom? A method to determine the contact patterns of adults that may lead to the spread of airborne infections. Proc Biol Sci. 1997; 264: 949-957.
  18. Bian L, Liebner D. A network model for dispersion of communicable diseases. Transactions in GIS. 2007; 11: 155-173.
  19. Travers J, Milgram S. An experimental study of the small world problem. Sociometry. 1969; 32: 425-443.
  20. Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks. Nature. 1998; 393: 440-442.
  21. Granovetter M. Threshold models of collective behavior. American journal of sociology. 1978; 83:1420-1443.
  22. Valente TW. Network Models of the Diffusion of Innovations. Cresskill: Hampton Press. 1995.
  23. Weinstein ND, Sandman PM. A model of the precaution adoption process: evidence from home radon testing. Health Psychol. 1992; 11: 170-180.
  24. Deffuant G, Huet S, Amblard F. An Individual-Based Model of Innovation Diffusion Mixing Social Value and Individual Benefit. American Journal of Sociology. 2005; 110: 1041-1069.
  25. Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation. 2002; 5: 1.
  26. Longini IM Jr, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings DA, et al. Containing pandemic influenza at the source. Science. 2005; 309: 1083-1087.
  27. Heymann DL. Control of Communicable Diseases Manual. 18th edn. Washington, DC: American Public Health Association. 2004.
  28. Longini IM Jr, Halloran ME, Nizam A, Yang Y. Containing pandemic influenza with antiviral agents. Am J Epidemiol. 2004; 159: 623-633.
  29. Chowell G, Miller MA, Viboud C. Seasonal influenza in the United States, France, and Australia: transmission and prospects for control. Epidemiol Infect. 2008; 136: 852-864.
  30. Ferguson NM, Cummings DA, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006; 442: 448-452.
  31. McKenzie FE. Smallpox models as policy tools. Emerg Infect Dis. 2004; 10: 2044-2047.
  32. Toy WC, Janosky JE, Laird SB. Influenza immunization of medical residents: knowledge, attitudes, and behaviors. Am J Infect Control. 2005; 33: 473-475.
  33. Nichol KL, Zimmerman R. Generalist and Subspecialist Physicians' Knowledge, Attitudes, and Practices Regarding Influenza and Pneumococcal Vaccinations for Elderly and Other High-Risk Patients. Arch Intern Med. 2001; 161: 2702-2708.

Citation: Mao L. A Relative Agreement Model for Simulating Human Decision Making and Preventive Behavior during Epidemics. Austin J Infect Dis. 2014;1(3): 7.