Ab Initio Investigation of Helium Interstitials in Y<sub>2</sub>Ti<sub>2</sub>O<sub>7</sub>: Kinetics and Bulk Moduli

Research Article

Ann Materials Sci Eng. 2015; 2(2): 1026.

Ab Initio Investigation of Helium Interstitials in Y2Ti2O7: Kinetics and Bulk Moduli

Danielson T¹* and Hin C1,2

¹Department of Materials Science and Engineering, Virginia Polytechnic Institute and State University, USA

²Department of Mechanical Engineering, Virginia Polytechnic Institute and State University, USA

*Corresponding author: Danielson T, Department of Materials Science and Engineering, Virginia Polytechnic Institute and State University, 460 Turner St, Blacksburg, VA, 24060, USA

Received: November 06, 2015; Accepted: December 28, 2015; Published: December 30, 2015

Abstract

Density functional theory has been used to investigate the migration barrier of a helium interstitial from one octahedral site to an adjacent octahedral site and the effects of octahedral helium interstitials on the bulk modulus of Y2Ti2O7. The interstitial is shown to travel through the tetrahedral location with an energetic barrier that can be largely attributed to the proximal location of the neighboring oxygen atom.

The bulk modulus has been investigated with up to three octahedral helium interstitials in Y2Ti2O7.

Keywords: Density Functional Theory; Nanostructured Ferritic Alloys; Irradiation; Defects

Abbreviations

NFAs: Nanostructured Ferritic Alloys; NCs: Nanoclusters; DFT: Density Functional Theory; GGA: Generalized Gradient Approximation; CI-NEB: Climbing Image Nudged Elastic Band

Introduction

The challenges opposing the efforts to develop materials systems for the next generation of fission reactors and future fusion reactors include; high neutron flux, high temperatures and pressures, corrosion and especially, embrittlement due to the transmutation product helium. Nanostructured ferritic alloys (NFAs) offer a promising solution to overcoming these challenges due to microstructural features such as a high stable dislocation density and a high number density of complex oxide nanoclusters (NCs) that serve to act as trapping sites for helium [1-4]. Despite experimental evidence of NCs acting as trapping sites, no concrete and complete theoretical understanding exists for the interaction of helium with the NCs and the resulting effects of its presence on the mechanical properties.

The migration barrier of helium in BCC iron is extremely low allowing helium to readily diffuse to preferential nucleation sites such as, dislocations, grain boundaries and voids [5-9]. Previous ab initio simulations have shown helium to have an attractive selfinteraction, making the formation of clusters favorable [5]. Likewise, the displacement cascade resulting from the kinetic energy transfer between an incident neutron and a constituent atom exacerbates the risk of growing bubbles as vacancies have been shown to stabilize the growth of helium bubbles [5,10,11]. Thus, a high concentration of vacancies coupled with the implantation of high-energy alpha particles promotes the risk of increased helium bubble formation. At high temperatures, helium bubbles become highly pressurized, resulting in damage to the surrounding lattice and potentially catastrophic cracking [12-15].

The complex oxide nanoclusters in NFAs exist in three main stoichiometric compositions; Y2Ti2O7, Y2O3 and Y2TiO5 [1]. Helium implanter transmission electron microscopy experiments carried out by Edmondson et al., have shown the effectiveness of NCs at trapping helium bubbles where the percentage of helium bubbles reaching grain boundaries is decreased by greater than 50% [9,16,17]. Similarly, due to the attractive self-interaction of helium, the bubbles trapped at the surface of NCs act as further trapping sites for helium diffusing through the matrix [15]. Thus, the trapping of helium at NCs has the potential to significantly mitigate the risk of helium embrittlement. Likewise, developing an understanding of the interactions of helium with the NCs and the effects of helium on their properties is of critical importance to further improving the ability to prevent helium embrittlement.

Further improvement of the prevention of helium embrittlement in candidate reactor materials relies heavily on the use of multiscale modeling that must be parameterized with large quantities of thermodynamic and kinetic information describing the matrix material, the oxide/matrix interface and the oxide [18-25]. Likewise, it is important to understand the changes that occur to the mechanical properties as a growing number of radiation induced defects, such as helium interstitials, are introduced.

Investigation of such quantities as the bulk modulus may help to understand why the oxides are well suited for trapping helium bubbles. Thus, this study deals with determining the migration barrier of helium in Y2Ti2O7 from the most stable interstitial site to an adjacent symmetry equivalent interstitial position and the effects of helium interstitials in Y2Ti2O7 on the bulk modulus.

Computational Methods

Density functional theory (DFT) as implemented by the VASP code [26-29] has been used in order to calculate the ground state properties of the migration path of helium and the bulk moduli of Y2Ti2O7 containing helium interstitials. One fully periodic unit cell has been used for each calculation where atoms are described by pseudopotentials generated with the projector-augmented wave method [30,31] and Brillouin zone integration is performed with a 4x4x4 k-point mesh. Due to the fact that DFT does not explicitly account for Van der Waals interactions, the ability of the pseudopotentials to accurately reproduce the interaction energy of a helium dimer at a variety of interatomic distances has been tested and compared to quantum Monte Carlo and configuration interaction simulations [32,33]. The generalized gradient approximation (GGA) from Perdew, Burke and Ernzerhoff (PBE) [34,35] best describes the behavior of the helium dimer. Thus, the GGA from PBE has been used to describe the exchange correlation effects where the semi-core 3p electrons and 4s and 4p electrons are treated as valence electrons for Ti and Y respectively.

In previous DFT calculations by Danielson and Hin [36,37] the four distinct helium interstitial positions in the Y2Ti2O7 unit cell and their relative stabilities have been determined. The interstitial positions (Figure 1) are the octahedral, tetrahedral, Y-Y and O-O configurations simply described as:

Figure 1: Four fully relaxed interstitial locations in Y2Ti2O7 as found previously by Danielson and Hin. Red, blue tan and black atoms represent Y, Ti, O and He respectively.

    

    
    

    

    Figure 1: Four fully relaxed interstitial locations in Y2Ti2O7 as found previously by Danielson and Hin. Red, blue tan and black atoms represent Y, Ti, O and He
respectively.
  • Octahedral: Located between Y and Ti atoms in (100) directions
  • Tetrahedral: Located on the O 8a vacancy tetrahedrally surrounded by Ti atoms
  • Y-Y: Located between two Y atoms in (110) directions prior to relaxation
  • O-O: Located at the midpoint of two O atoms prior to relaxation

The octahedral interstitial location is the most energetically preferable site for the helium interstitial to occupy and thus, the migration of helium from one octahedral site to an adjacent octahedral site, as well as the mechanical properties of the oxide containing increasing numbers of helium interstitials on octahedral sites is the focus of this study.

The migration barrier and migration path of a helium interstitial traveling between adjacent octahedral locations has been investigated using the climbing image nudged elastic band (CI-NEB) method as implemented by VASP and G. Henkelman [38-40]. The NEB works by linearly interpolating the geometry of the cell using a string of images connecting the initial and final states of the diffusion pathway. Each image is connected by a spring with a constant, k, and is relaxed to its ground state energy using a force projection scheme where potential forces act perpendicular to the band and the spring forces act along the band. As each image is relaxed to its ground state, the minimum energy path is determined. The climbing image NEB uses these same principles, except in this case, the highest energy image climbs to the saddle point and feels no spring forces. The nudged elastic band relaxes each image with a fixed cell shape and volume into its ground state rendering the migration barrier and path [39,40].

The bulk modulus of Y2Ti2O7 has been calculated by applying strain in the x,y, and z directions in the range of +/- 6% in increments of 0.5%. In order to maintain the perfect cubic symmetry, the pure crystal has been first relaxed to its ground state and subsequently helium interstitials are introduced on the octahedral sites. In order to investigate the effects of increasing concentrations of helium, up to three helium interstitials have been introduced. The single octahedral helium interstitial configuration can be seen in Figure 1 and the two and three helium interstitial configurations can be seen in Figure 2. The two and three helium interstitial configurations have been chosen based on the work from L. Yang et al. [41], and represent three of the most energetically stable multi-octahedral interstitial configurations. From first-principles the bulk modulus can be calculated by performing a polynomial fit to the energy-volume data obtained and substituting the equilibrium volume as:

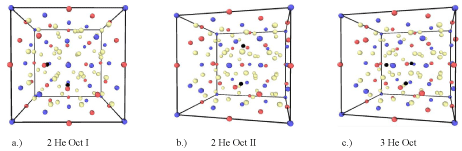
Figure 2: a.) Y2Ti2O7 containing two octahedral interstitials where Y and Ti are oriented in the same direction, b.) two octahedral interstitials where Y and Ti are oriented in opposite directions and c.) three octahedral helium interstitials, red, blue, tan and black atoms represent Y, Ti, O and He respectively.

    

    
    

    

    Figure 2: a.) Y2Ti2O7 containing two octahedral interstitials where Y and Ti are oriented in the same direction, b.) two octahedral interstitials where Y and Ti are
oriented in opposite directions and c.) three octahedral helium interstitials, red, blue, tan and black atoms represent Y, Ti, O and He respectively.

B= V 0 d 2 E(V) d V 2 MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiabg2da9iaadAfadaWgaaWcbaGaaGimaaqabaGcdaWcaaqaaiaadsgadaahaaWcbeqaaiaaikdaaaGccaWGfbGaaiikaiaadAfacaGGPaaabaGaamizaiaadAfadaahaaWcbeqaaiaaikdaaaaaaaaa@4121@

where, V0 is the equilibrium volume.

Results

Migration from octahedral to octahedral interstitial locations

In order to determine the migration barrier and the migration path of the helium interstitial between two of the most stable sites (i.e. octahedral to octahedral), the CI-NEB method has been used. Nine intermediate images define a straight-line path between the two locations and each image is fully relaxed to its lowest energy state defining the migration path. The un-relaxed and relaxed migration paths are shown in Figure 3.

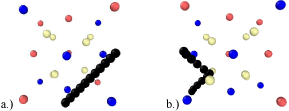
Figure 3: a.) Unrelaxed and b.) relaxed migration paths from octahedral to octahedral location red, blue, tan and black spheres represent Y, Ti, O and He respectively.

    

    
    

    

    Figure 3: a.) Unrelaxed and b.) relaxed migration paths from octahedral to octahedral location red, blue, tan and black spheres represent Y, Ti, O and He
respectively.

Upon full relaxation of the migration path, the helium interstitial is found to travel from one octahedral location to the neighboring octahedral location via the tetrahedral location. The migration barrier for this path is shown in Figure 4. The barrier from the octahedral location to the tetrahedral location was found to be 1.336 eV where the majority of the energetic barrier appears to be attributed to the proximal location of the neighboring oxygen atom. Once the helium atom reaches the vacancy, it can then continue its path to the adjacent octahedral location upon overcoming the migration barrier of 0.802 eV.

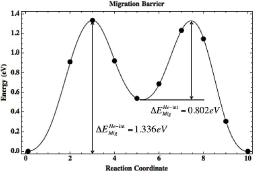
Figure 4: Migration barrier from one octahedral interstitial location to an adjacent octahedral location in Y2Ti2O7

    

    
    

    

    Figure 4: Migration barrier from one octahedral interstitial location to an
adjacent octahedral location in Y2Ti2O7

Bulk modulus of Y2Ti2O7 containing helium interstitials

In order to determine the effect of the most energetically preferable helium interstitials on the mechanical properties of the oxide, the bulk modulus has been calculated. The bulk modulus of pure Y2Ti2O7 has been calculated and confirmed with existing DFT calculations [42] as 183.031 GPa, the energy volume-data is shown in Figure 5.

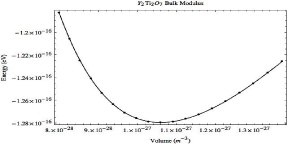
Figure 5: Energy-volume curve for pure Y2Ti2O7.

    

    
    

    

    Figure 5: Energy-volume curve for pure Y2Ti2O7.

In the case of pure Y2Ti2O7, it is obvious that there is no internal displacement of the constituent atoms from their equilibrium lattice sites. In this case, all bonds are at equilibrium and no internal strain exists. This is no longer true upon introduction of helium interstitials. Figure 6 shows the difference in the internal structure for the fully relaxed interstitial configurations tested. Similarly, Table 1 shows the calculated net displacement of the constituent atoms for the relaxed structure at 0% volumetric strain. The net displacement of atoms has been calculated by taking the sum of the displacement of each type of atom from its equilibrium position in pure Y2Ti2O7. It can be noted that there is an increasing amount of displacement of atoms from their equilibrium sites with the addition of each helium atom. While Figure 6b and Figure 6c both have two helium interstitials the net displacement of oxygen atoms is less than in Figure 6c.

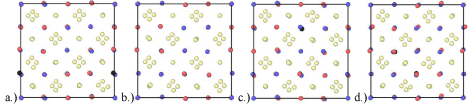
Figure 6: Fully relaxed internal structure for a.) single octahedral interstitial, b.) two octahedral interstitials (2HeOctI), c.) two octahedral interstitials (2HeOctII) and d.) three octahedral interstitials where, red, blue, tan and black atoms are Y, Ti, O and He atoms respectively.

    

    
    

    

    Figure 6: Fully relaxed internal structure for a.) single octahedral interstitial, b.) two octahedral interstitials (2HeOctI), c.) two octahedral interstitials (2HeOctII) and
d.) three octahedral interstitials where, red, blue, tan and black atoms are Y, Ti, O and He atoms respectively.

Table 1: Calculated bulk moduli in GPa and net displacement in nm of all constituent Y, Ti and O atoms.





  

    
Bulk    Modulus 

    
Net    Displacement Y 

    
Net    Displacement Ti 

    
Net    Displacement O 

  

  

    
Y2Ti2O7 

    
183.031 

    
- 

    
- 

    
- 

  

  

    
Octahedral 

    
167.363 

    
.01656 

    
.01774 

    
.03081 

  

  

    
2 He Oct    I 

    
160.139 

    
.02072 

    
.01917 

    
.03834 

  

  

    
2 He Oct    II 

    
151.301 

    
.01906 

    
.01606 

    
.04310 

  

  

    
3 He Oct 

    
142.185 

    
.02473 

    
.02051 

    
.04406 

  









Table 1:  Calculated bulk moduli in GPa and net displacement in nm of all constituent Y, Ti and O atoms.

In calculating the bulk modulus for the different octahedral configurations, care has been taken to ensure that only volumetric strains in the elastic region are accounted for. The bulk modulus and the displacement of the constituent atoms are shown in Table 1 for each octahedral configuration. The bulk modulus decreases with the addition of each interstitial indicating that the addition of helium interstitials makes the oxide softer.

Discussion

The migration path of helium from one octahedral site to an adjacent octahedral site has been found to travel through the vacancy lying on the tetrahedral interstitial location. The tetrahedral interstitial has a higher solution energy than the octahedral interstitial site, as found by previous DFT studies [36,37,41]. The vacant site located on the tetrahedral location however provides a large amount of volume for the helium interstitial to travel through. Both energetic barriers are considerably higher than the migration barrier of helium in BCC iron (0.07 eV). Likewise, it is apparent that a helium interstitial that is occupying a tetrahedral interstitial site is more likely to travel to an octahedral site than the opposite due to the lower migration barrier. The trapping of helium at NCs in NFAs is often attributed to the interaction between the oxygen atoms and the helium atoms [43]. The majority of the migration barrier was noted to arise from the need to displace the oxygen atom in order for the helium interstitial to pass making this idea credible.

The bulk modulus was found to decrease with increasing helium concentration indicating that the oxides become softer as the helium content increases. It should be noted that Figure 6a-d shows each of the interstitial configurations tested in order of lowest to highest net oxygen displacement. The increasingly strained bonds affect the bulk modulus in that the more internal strain that exists, the less stress that can be applied to the structure before significant deformation occurs. The decrease in the bulk modulus may shed some light on the trapping mechanisms of the oxides. If we make the assumption that some single helium interstitials are contained within the oxide lattice, we can assume that the bulk modulus has decreased. Now a bubble that has formed (and is growing) at the oxide-iron interface will increasingly be able to deform the oxide. Considering the helium bubble to be pressurized, this deformation of the oxide lattice would ultimately decrease the pressure of the helium bubble increasing the stability.

Conclusion

The migration of a helium interstitial between two of the most energetically preferential sites in the Y2Ti2O7 lattice was investigated using the nudged elastic band. The migration path was found to travel from octahedral to tetrahedral to octahedral location. The barrier from the octahedral to tetrahedral location is 1.336 eV and the barrier from the tetrahedral to octahedral location is 0.802 eV where the majority of the energetic barrier arises from displacing an oxygen atom in order for the helium interstitial to pass by. The bulk modulus of Y2Ti2O7 was investigated containing increasing concentrations of helium up to three helium interstitials occupying octahedral interstitial sites. The bulk modulus was found to decrease with increasing helium concentration indicating a softening of the oxides when helium is present.

Acknowledgement

The authors acknowledge Advanced Research Computing at Virginia Tech for providing computational resources and technical support that have contributed to the results reported within this paper.

References

  1. Odette GR, Alinger MJ, Wirth BD. Recent Developments in Irradiation- Resistant Steels. Annu. Rev. Mater. Res. 2008; 38: 471.
  2. Schneibel JH, Heilmaier M, Blum W, Hasemann G, Shanmusgasundaram T. Temperature dependence of the strength of fine and ultrafine-grained materials. Acta Mat. 2011; 59: 1300.
  3. Kleuh RL, Maziasz PJ, Kim IS, Heatherly L, Hoelzer DT, Hashimoto N, et al. Tensile and creep properties of an oxide dispersion-strengthened ferritic steel. J Nucl Mater. 2002; 307-311: 773.
  4. McClintock DA, Hoelzer DT, Sokolov MA, Nanstad RK. Mechanical properties of neutron irradiated nanostructured ferritic alloy 14 YWT. J Nucl Mater. 2009; 368-388: 307.
  5. Fu CC, Willaime F. Ab initio study of helium in a-Fe: Dissolution, migration and clustering with vacancies. Phys Rev B. 2005; 72: 064117.
  6. Yamamoto T, Odette GR, Kurtz RJ, Wirth BD. A multi-scale model of helium transport and fate in irradiated tempered martensitic steels and nanostructured ferritic alloys. Fusion Reactor Materials Program. 2010; DOE/ ER-0313/49:73.
  7. Heinisch HL, Gao F, Kurtz RJ. Modeling the interaction helium with dislocations and grain boundaries in alpha-iron. J ASTM Internat. 2007; 4.
  8. Al-Hajji JN, Ghoniem NM. Nucleation of grain boundary cavities under the influence of helium and applied stress. Acta Metall. 1987; 35: 1067.
  9. Edmondson PD, Parish CM, Zhang Y, Hallen A, Miller MK. Helium bubble distributions in a nanostructured ferritic alloy. J Nucl Mater. 2013; 434: 210.
  10. Erhart P. A first-principles study of helium storage in oxides and at oxide— iron interfaces. J Appl Phys. 2012; 111: 113502.
  11. Morishita K, Sugano R, Wirth BD, Diaz de la Rubia T. Thermal stability of helium vacancy clusters in iron. Nucl Instrum Methods Phys Res B. 2003; 202: 76.
  12. Ishizaki T, Xu Q, Yoshiie T, Nagata S, Troev T. The effect of hydrogen and helium on microvoid formation in iron and nickel. J Nucl Mater. 2002; 307- 311: 961.
  13. Hafez Haghighat SM, Lucas G, Schaublin R. State of a pressurized helium bubble in iron. EPL. 2009; 85: 60008.
  14. Sagues AA, Schroeder H, Kesternich W, Ullmaier H. The influence of helium on the high temperature mechanical properties of an austenitic stainless steel. J Nucl Mater. 1978; 78: 289.
  15. Trinkaus H. On the modeling of the high temperature embrittlement of metals containing helium. J Nucl Mater. 1983; 118: 39.
  16. Odette GR, Miao P, Edwards DJ, Yamamoto T, Kurtz RJ, Tanigawa H. Helium transport, fate and management in nanostructured ferritic alloys: In situ helium implanter studies. J Nucl Mater. 2011; 417: 1001.
  17. Edmondson PD, Parish CM, Zhang Y, Hallen A, Miller MK. Helium entrapment in a nanostructured ferritic alloy. Scripta Mat. 2011; 65: 731.
  18. Hin C, Wirth BD, Neaton JB. Formation of Y2O3 nanoclusters in nanostructured ferritic alloys during irradiation of isothermal and anisothermal heat treatment: A kinetic Monte Carlo study. Phys Rev B. 2009; 80: 134118.
  19. Hin C, Brechet Y, Maugis P, Soisson F. Kinetics of heterogeneous grain boundary precipitation of NbC in a-iron: A Monte Carlo study. Acta Mat. 2008; 56: 5653.
  20. Hin C. Kinetics of heterogeneous grain boundary precipitation of Ni3Al in nickel alloy. J Phys D: Appl Phys. 2009; 42: 225309.
  21. Hin C. Kinetic Monte Carlo Simulations of Anisotropic Lithium Intercalation into LixFePO4 Electrode Nanocrystals. Advanced Functional Mater. 2011; 21: 2477.
  22. Hin C. Nanostructured Ferritic Alloys as Future Materials for Generation IV and Fusion Reactors. In: Wythers MC, editor. Microalloying: Concepts, Processes and Applications. Nova Publishers. 2011; 6.
  23. Hin C, Dresselhaus M, Chen G. Vacancy clustering and diffusion in heavily P doped Si. Appl Phys Lett. 2010; 97: 251909.
  24. Hin C, Brechet Y, Maugis P, Soisson F. Kinetics of heterogeneous dislocation precipitation of NbC in alpha-iron. Acta Mat. 2008; 56: 5535.
  25. Hin C, Brechet Y, Maugis P, Soisson F. Heterogeneous precipitation on dislocations: effect of the elastic field on precipitate morphology. Phil Mag. 2008; 88: 1555.
  26. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B Condens Matter. 1993; 47: 558-561.
  27. Kresse G, Hafner J. Ab initio molecular-dynamics simulation of the liquidmetal- amorphous-semiconductor transition in germanium. Phys Rev B Condens Matter. 1994; 49: 14251-14269.
  28. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996; 54: 11169-11186.
  29. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996; 54: 11169-11186.
  30. Blöchl PE. Projector augmented-wave method. Phys Rev B Condens Matter. 1994; 50: 17953-17979.
  31. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. 1999; 59: 1758.
  32. van Mourik T, van Lenthe JH. Benchmark full configuration interaction calculations on the helium dimer. J Chem Phys. 1995; 102: 7479.
  33. Ceperley DM, Partridge H. The He2 potential at small distances. J Chem Phys. 1986; 84: 821.
  34. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett. 1996; 77: 3865-3868.
  35. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett. 1997; 78: 1396.
  36. Danielson T, Hin C. Structural and electronic effects of helium interstitials in Y2Ti2O7: A first-principles study. J Nucl Mater. 2014; 452: 189.
  37. Danielson T, Hin C. Helium interaction with Y2Ti2O7: A first-principles study. Mater Res Soc Symp Proc. 2014; 1645.
  38. Jonsson H, Mills G, Jacobsen KW. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In: Berne BJ, Ciccotti G Coker DF, editors. Classical and Quantum Dynamics in Condensed Phase Simulations. World Scientific. 1998.
  39. Henkelman G, Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J Chem Phys. 2000; 113: 9901-9904.
  40. Henkelman G, Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J Chem Phys. 2000; 113: 9978-9985.
  41. Yang L, Jiang Y, Odette GR, Yamamoto T, Liu Z, Liu Y. Trapping helium in Y2Ti2O7 compared to in matrix iron: A first principles study. J Appl Phys. 2014; 115: 143508.
  42. Jiang Y, Smith JR, Odette GR. Prediction of structural, electronic and elastic properties of Y2Ti2O7. Acta Mat. 2010; 58: 1536.
  43. Edmondson PD, Parish CM, Li Q, Miller MK. Thermal stability of nanoscale helium bubbles in a 14YWT nanostructured ferritic alloy. J Nucl Mater. 2014; 445: 84-90.

Citation: Danielson T and Hin C. Ab Initio Investigation of Helium Interstitials in Y2Ti2O7: Kinetics and Bulk Moduli. Ann Materials Sci Eng. 2015; 2(2): 1026. ISSN : 2471-0245