Gudes O; Ball SJ; Dur F; Burke M; Varhol R

Review Article

Austin J Public Health Epidemiol. 2015;2(1): 1014.

The Association between Urban Form and Ischemic Heart Disease: Evidence from Brisbane, Australia

Gudes O1,2*, Ball SJ3, Dur F4, Burke M5 and Varhol R6

¹Department of Spatial Sciences, Curtin University, Australia

²Centre for Community Science, Griffith University, Australia

³Telethon Kids Institute, University of Western Australia, Australia

⁴Environment and Sustainability Branch, Logan City Council, Australia

⁵Urban Research Program, Griffith University, Australia

⁶Department of Health Policy & Management and Health Information Management, Curtin University, Australia

*Corresponding author: Gudes O, Department of Spatial Sciences, Curtin University and Centre for Community Science, Griffith Health Institute, Griffith University, Australia

Received: January 13, 2015; Accepted: March 28, 2015; Published: March 31, 2015

Abstract

We measured the association between urban form and hospitalisation rates for Ischaemic Heart Disease (IHD), stratified by age and sex, and controlling for ethnicity, socioeconomic status, proximity to hospital and neighbourhood walkability. This was a retrospective cohort study of the proportion of people within the Brisbane area of Australia, which were hospitalised between 2006 to 2011 with a primary diagnosis of IHD. There were strong spatial patterns in the incidence of IHD. The importance of predictor variables differed by sex and age. Urban form was generally not a strong predictor. This study suggests no strong relationship was identified between urban form factors and ischemic heart disease using this research approach.

Keywords: Ischaemic heart disease; Urban form and structure; Spatial analysis

Introduction

Ischaemic Heart Disease (IHD) is characterised by reduced blood supply to the heart. It is one of the most common causes of mortality world-wide, resulting in 11.2% of deaths globally in 2011 [1]. In Australia, IHD accounts for 16% of all deaths [2], placing it 9th internationally in terms of contribution to national burden of disease. Major risk factors of this disease include family history of coronary artery disease, diabetes, high blood pressure or atherosclerosis, smoking, poor nutrition (especially dietary fat intake), previous heart attack or stroke, obesity, hypertension, elevated cholesterol and/or low level of High Density Lipoprotein (HDL) [3].

The built environment is highlighted as a factor determining health outcomes, as part of a broader social determinants model of health [4], yet very little is known about the effects of urban form on IHD. It has recently been proposed that urban form (the physical shape and structure of a city that influences daily activity)is an important behavioural determinant [5]. Previous studies have related urban form to travel behaviour, walking and other forms of physical activity [6,7], air pollution [8] and obesity [9,10]. These effects may be of some significance for IHD. The aim of this study paper is to test for an association between urban form and the incidence of IHD in Brisbane, Australia’s third largest city. We also control for the effects of age, sex, ethnicity, socioeconomic status, proximity to hospital and neighbourhood walkability.

Methodological approach, design and settings

This study was a retrospective cohort study of spatial variation in the incidence of hospitalisations due to IHD in southern metropolitan Brisbane, Australia (Figure 1) from 1 January 2006 to 31 December 2011. Brisbane is the third largest city in Australia, with a population of 2.07 million in 2011 [11]. The spatial units were Statistical Local Areas (SLAs), as defined by the Australian Bureau of Statistics [11]. Here after the term �study area� refers to the 118 SLAs used for analysis (Figure 2).

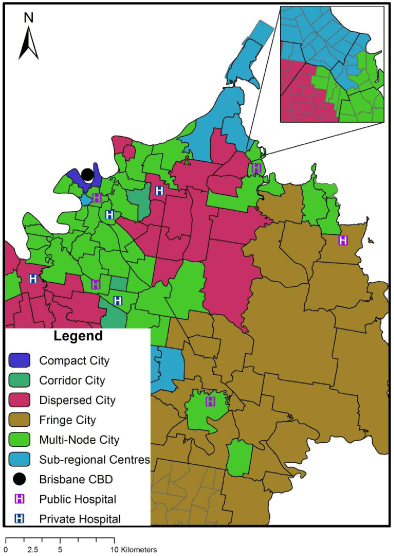
Figure 1: Area of the study with assigned urban form categories by Statistical Local Areas (SLAs).

    
    
    Figure 1:  Area of the study with assigned urban form categories by Statistical
Local Areas (SLAs).

Figure 2: Walkability index map for the 118 SLAs in the area of study.

    
    
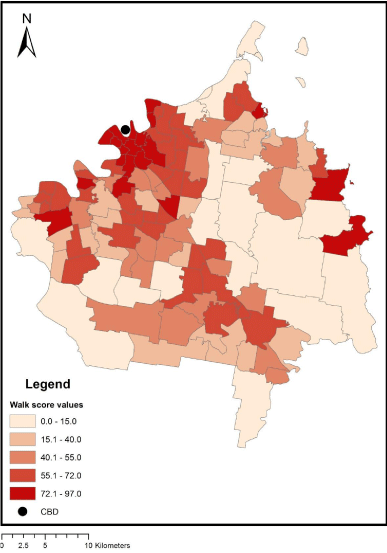
    Figure 2:  Walkability index map for the 118 SLAs in the area of study.

The analysis was stratified by age and sex. Our methodological approach was based on three phases: 1) Adoption of methods suggested by [5,12]. The data collection and the categories of the data aggregation were replicated by [5] within Brisbane; 2) Aggregation of the total IHD hospitalizations between 2006 and 2011 into Statistical Local Areas (SLAs) level; and 3) Bayesian modeling was undertaken in order to understand the relationships between the urban form categories and IHD hospital admission measures, which simultaneously allowed urban form to be evaluated as a risk predictor. This model also accounted for socioeconomic status, including proximity to public and private hospitals, ethnicity and walking index. The following sections provide detailed information about our methodological approach, design and settings.

Urban form classification

We assigned each Statistical Local Area one of six urban form categories (Table 1), following Grosvenor and O’Neill [5]. We initially assigned this classification at the finer spatial scale of Statistical Areas Level 1 (ABS 2011) and then determined the urban form category for each SLA.

Table 1: Urban form classification in Brisbane, Queensland (derived from: Grosvenor & O’Neill, 2012(5).




  
    Urban form    category 
    Description 
    GIS criteria /    process 
  
  
    Compact City
    General    increase in accessibility to public transport, employment, retail and    essential services with a mixture of housing choice.
    1500m from    Brisbane CBD.
  
  
    Multi-Node    City
    Highly    accessible to public transport, employment, retail and essential services as    the Compact City but dominated by apartments.
    Within 800 m    of "Principal Regional Activity    Centres"of South East Queensland Regional Plan (SEQRP) and within    800m proximity to railway and bus way stations
  
  
    Sub-regional    Centres
    SA1s located    within 800m of railway stations (proxy for centroid) located within    designated secondary centres: Sub-regional centres have similar    characteristics to the Multi-Node City on a smaller scale with less    employment opportunities.
    SA1s in the suburbs within 800 m buffer of    "Major regional" and "Specialist" Activity Centres (See    South East Queensland regional Plan 2009-2031 report) and within 800m    proximity to railway and bus way stations.
  
  
    Corridor    City
    Any SA1s    outside the previous categories that are located within 800m walking distance    of a railway station within the rest of the metropolitan area or 400m of a    high-order bus corridor. This area Characterised by good accessibility to    local shopping precincts with a mixture of housing choice (other than    four-storey and above apartments).
    SA1 within 400 m buffer of the bus stops on the    road ways and major bus routes (Grosvenor & O’Neill (2012)and within 800m    of railway stations which are not assigned a urban form definition category    previously 
  
  
    Dispersed City
    Any other    areas left within what is considered the traditional Brisbane suburban    environment. Generally comprises a mixture of old and contemporary detached    dwellings dominated by car access and local bus services.
    All SA1s    within 400m vicinity of all bus stops (from the remaining SA1s from the    previous steps).
  
  
    Fringe    City
    Designated    areas beyond traditional suburban environments (primarily contemporary build)    with poor public transport and local service accessibility.
    All other SA1s    which are not selected in any previous steps



Table 1:  Urban form classification in Brisbane, Queensland (derived from: Grosvenor & O’Neill, 2012(5).

Ethnicity

The following cultural groups were accounted for in the model based on the ABS’s main categories in 2006 [13] and 2011 [14] censuses, and the categories provided in our dataset: Americas, North Africa and the Middle East, North-east Asia, North-west Europe, Oceania and Antarctica (people who were born in Australia), Southeast Asia, Southern and central Asia, Southern and eastern Europe, Sub-Saharan, Africa and Not stated (Table 2).

Table 2: Proportion of people hospitalised with ischaemic heart disease as a primary diagnosis.




  
    40-44 years old 
     
     
  
  
     
    Female
    Male
  
  
    Ethnic category
    Cases
    Pop.
    Prop.
    Cases
    Pop.
    Prop.
  
  
    Oceania and Antarctica
    146
    22644
    0.0064
    394
    21416
    0.0184
  
  
    South-east Asia
    3
    2103
    0.0014
    17
    1530
    0.0111
  
  
    Southern and Central Asia
    6
    629
    0.0095
    9
    707
    0.0127
  
  
    North-east Asia
    1
    1310
    0.0008
    2
    905
    0.0022
  
  
    Southern and Eastern Europe
    6
    894
    0.0067
    9
    780
    0.0115
  
  
    North-west Europe
    7
    2769
    0.0025
    47
    2949
    0.0159
  
  
    Sub-Saharan Africa
    2
    879
    0.0023
    15
    837
    0.0179
  
  
    North Africa and Middle East
    1
    369
    0.0027
    7
    514
    0.0136
  
  
    Americas
    3
    518
    0.0058
    4
    470
    0.0085
  
  
    Not stated
    5
    1576
    0.0032
    12
    1794
    0.0067
  
  
    TOTAL
    180
    33691
    0.0053
    516
    31902
    0.0162
  
  
    50-54 years old 
     
     
  
  
     
    female
    male
  
  
    Ethnic category
    cases
    population
    proportion
    cases
    population
    proportion
  
  
    Oceania and Antarctica
    431
    19701
    0.0219
    983
    18571
    0.0529
  
  
    South-east Asia
    24
    1893
    0.0127
    28
    1394
    0.0201
  
  
    Southern and Central Asia
    10
    529
    0.0189
    31
    505
    0.0614
  
  
    North-east Asia
    4
    1196
    0.0033
    10
    937
    0.0107
  
  
    Southern and Eastern Europe
    13
    1127
    0.0115
    57
    1120
    0.0509
  
  
    North-west Europe
    51
    2634
    0.0194
    109
    2870
    0.0380
  
  
    Sub-Saharan Africa
    7
    499
    0.0140
    30
    628
    0.0478
  
  
    North Africa and Middle East
    3
    161
    0.0186
    12
    251
    0.0478
  
  
    Americas
    11
    461
    0.0239
    13
    462
    0.0281
  
  
    Not stated
    13
    1371
    0.0095
    17
    1488
    0.0114
  
  
    TOTAL
    567
    29572
    0.0192
    1290
    28226
    0.0457
  
  
    60-64 years old 
     
     
  
  
     
    female
    male
  
  
    Ethnic category
    cases
    population
    proportion
    cases
    population
    proportion
  
  
    Oceania and Antarctica
    666
    13818
    0.0482
    1514
    13074
    0.1158
  
  
    South-east Asia
    25
    1070
    0.0234
    36
    823
    0.0437
  
  
    Southern and Central Asia
    11
    205
    0.0537
    28
    406
    0.0690
  
  
    North-east Asia
    15
    665
    0.0226
    25
    601
    0.0416
  
  
    Southern and Eastern Europe
    38
    867
    0.0438
    97
    1033
    0.0939
  
  
    North-west Europe
    128
    3051
    0.0420
    310
    3358
    0.0923
  
  
    Sub-Saharan Africa
    5
    259
    0.0193
    22
    340
    0.0647
  
  
    North Africa and Middle East
    2
    53
    0.0377
    15
    101
    0.1485
  
  
    Americas
    11
    215
    0.0512
    20
    374
    0.0535
  
  
    Not stated
    10
    1005
    0.0100
    27
    1071
    0.0252
  
  
    TOTAL
    911
    21208
    0.0430
    2094
    21181
    0.0989
  
  
    70-74 years old 
     
     
  
  
     
    female
    male
  
  
    Ethnic category
    cases
    population
    proportion
    cases
    population
    proportion
  
  
    Oceania and Antarctica
    735
    7561
    0.0972
    1142
    6209
    0.1839
  
  
    South-east Asia
    33
    515
    0.0641
    14
    400
    0.0350
  
  
    Southern and Central Asia
    11
    89
    0.1236
    24
    68
    0.3529
  
  
    North-east Asia
    7
    377
    0.0186
    21
    379
    0.0554
  
  
    Southern and Eastern Europe
    64
    782
    0.0818
    122
    795
    0.1535
  
  
    North-west Europe
    136
    1792
    0.0759
    287
    1887
    0.1521
  
  
    Sub-Saharan Africa
    8
    52
    0.1538
    14
    43
    0.3256
  
  
    North Africa and Middle East
    9
    24
    0.3750
    11
    22
    0.5000
  
  
    Americas
    6
    57
    0.1053
    10
    69
    0.1449
  
  
    Not stated
    11
    647
    0.0170
    9
    614
    0.0147
  
  
    TOTAL
    1020
    11896
    0.0857
    1654
    10486
    0.1577
  
  
    80-84 years old 
     
     
  
  
     
    female
    male
  
  
    Ethnic category
    cases
    population
    proportion
    cases
    population
    proportion
  
  
    Oceania and Antarctica
    906
    5665
    0.1599
    783
    3356
    0.2333
  
  
    South-east Asia
    23
    177
    0.1299
    15
    93
    0.1613
  
  
    Southern and Central Asia
    13
    58
    0.2241
    13
    12
    0.9900
  
  
    North-east Asia
    9
    214
    0.0421
    10
    143
    0.0699
  
  
    Southern and Eastern Europe
    80
    571
    0.1401
    95
    525
    0.1810
  
  
    North-west Europe
    150
    1245
    0.1205
    179
    1017
    0.1760
  
  
    Sub-Saharan Africa
    11
    25
    0.4400
    3
    11
    0.2727
  
  
    North Africa and Middle East
    5
    32
    0.1563
    8
    15
    0.5333
  
  
    Americas
    11
    22
    0.5000
    8
    22
    0.3636
  
  
    Not stated
    9
    729
    0.0123
    15
    522
    0.0287
  
  
    TOTAL
    1217
    8738
    0.1393
    1129
    5716
    0.1975



Table 2:  Proportion of people hospitalised with ischaemic heart disease as a primary diagnosis.

Socioeconomic status

Socioeconomic Status (SES) was based on the 2006 Australian Bureau of Statistics’ Index of Relative Socioeconomic Advantage/ Disadvantage [15]. This index, which is generated for each fiveyearly national census, summarises the presence of both positive and negative social and economic factors (e.g. income, educational attainment and unemployment) of people and households within specific geographical areas. In deriving the Index, the Australian Bureau of Statistics used a Principal Components Analysis to assign each variable a weighting. Individual census areas are then given a score based on the sum of their variable weightings.

Neighbourhood walkability

One way that built environment elements are organised and measured in research for active travel is with a ‘walkability index’. The most widely known and a popularly used measure is Walk Score^® [16] (see https://www.walkscore.com) which uses Google Maps and distance-based algorithms to measure and score accessibility on foot to a range of amenities (destinations) in a certain neighbourhood. In this study we used the Walk Score website [17] to apply these metrics in our area of study. In each of the 118 SLAs we located the geographic centroids and then extracted the associated walking score as appropriate. See Figure 2 for the walkability index by SLAs.

Distance to the nearest cardiology centre

The distance to cardiology centres (based on public and private hospitals) was identified by de Andade et al. [18] as an important measure. For example they found a positive association between IHD mortality rates and the geographic distances between patients city of residence and their corresponding regional cardiology centres. Subsequently, we derived some of our methodological work from their recommendations, as in the case of the network analysis tool in ArcGIS 10.2, which was used to measure the street (network) distance.

Hospitalisation data

Hospitalisation data were sourced from the Queensland Health Statistics Unit, in the form of a database of hospitalisation records in the south metro Brisbane area of Queensland, dating back to 2006. For each SLA, we calculated the total number of people, stratified by age, sex and ethnicity, which had one or more hospitalisations from the first of January 2006 to the 31^st of December 2011, with a primary diagnosis of IHD (ICD-10 codes I20-I25). This approach ignored information pertaining to the number of different hospitalisation events per person, and length of stay. We restricted the analysis to people over 39 years of age given that ischaemic heart disease is uncommon below 40 years [19,20], and to people under 85 years of age due to low numbers of people older than 84.

Stratification by age and sex

Stratification was undertaken by grouping the sample by age and sex to allow for demographic diversity in the spatial distribution of IHD. Such differences may arise if there are demographic discrepancies in the relative importance of different risk factors, including urban form. The population was grouped into five-year age categories given that there is a steep relationship between age and heart disease [19,20]. Further, we restricted the analysis to the first five years of every decade, so that there were a manageable number of age categories while still covering a wide distribution of ages. Thus we analysed the data for the following age categories: 40-44, 50-54, 60-64, 70-74 and 80-84 years. For each individual who had more than one hospitalisation with a primary diagnosis of ischaemic heart disease in the period 2006 to 2011, we based their age category on the time of their first hospitalisation.

Population denominators

We used population census data (14) for population denominators and estimated the population denominator for each SLA, stratified by age, sex and ethnicity, as the average number of people for the 2006 and 2011 censuses [13,14]. Fractional averages were rounded to integer values, using a random number generator to determine whether to round up or down.

Statistical Analyses

R_i ~Binomial (N_i,p_i)

logit(p_i) = β0 (1) null model

where, for area i, R_i is the number of people who were hospitalised at least once for ischemic heart disease as the primary diagnosis, N_i is the total number of people of age and sex category, and p_i is the probability of being hospitalised for ischemic heart disease. The constant β₀ is the log odds of the mean probability of being hospitalised.

We used a random effects model to allow for variation between areas in the probability of ischemic hospitalisation:

Logit (p_i)= β0+ u_i+ v_i (2) random effects model

where u_i is a spatially-correlated random effect and v_i is a spatiallyuncorrelated random effect, following [21]. The uncorrelated random effect was specified as being normally distributed with a mean of zero, and no constraint of correlation among neighbouring areas.

The spatially correlated random effect u_i was based on a Conditional Autoregressive (CAR) term, with the constraint of following a normal distribution that is conditional on the local mean of CAR random effect estimates among neighbouring areas:

$[u_{i} | u_{j}, i \neq j, σ_{u}^{2}] \sim N (\bar{u_{i},})$

$[u_{i} | u_{j}, i \neq j, σ_{u}^{2}] \sim N (\bar{u_{i}, σ_{i}^{2}})$

where $\bar{u_{i}} = \frac{\sum_{j} u_{j} ω_{i j}}{\sum_{j} ω_{i j}}$

$σ_{i}^{2} = \frac{σ_{u}^{2}}{\sum_{j} ω_{i j}}$

ω_ij= 1 if areas i and j are neighbours; otherwise 0

Neighbours were defined as those areas immediately adjacent to the area in question, including neighbours that share only one vertex.

Standardisation for ethnicity

We used an offset term to standardise the models by ethnicity:

logit(p_i) = β₀+ logit(e_i) (3) ethnically-adjusted null model

and

logit(p_i) = β₀+ logit(e_i) + u_i + v_i

(4) ethnically-adjusted random effects model

where ei is the expected proportion of people hospitalised in area i based on the proportion of different ethnic groups within that area, and the global (all-of-study-area) proportion of people hospitalised for each ethnic group. This standardisation was calculated separately for each age-sex demographic class (Table 2), and it shows the proportion of people hospitalised with ischemic heart disease as a primary diagnosis, by ethnic group, stratified by demographic class.

We used a mixed model to allow for the effects of urban form and other covariates, while standardising for ethnicity and allowing for spatially-correlated and spatially-uncorrelated random effects:

legit(p_i) = β₀+ legit(e_i) + β₁.X₁ +...+βn.Xn+ u_i + v_i

(5) ethnically-adjusted mixed model

where β₁...β_n are covariate effects. We ran uni variable versions of this model, plus a full model that included effects of all covariates.

Each model was run as a Bayesian analysis. Bayesian techniques have a proven ability to solve disease mapping problems through the use of Markov Chain Monte Carlo sampling methods [23]. We specified uninformative normal prior distributions ( = 0; s = 1000) for each of β₀, β₁…β_n, and following [24] we specified uninformative halfnormal prior distributions (μ = 0; σ = 100) for the standard deviation of each of the random effects u, v and d. We used Win BUGS 1.4 software [25], which uses Markov Chain Monte Carlo sampling to generate posterior distributions. For each model we used a burn-in of 1000,000 iterations, with posterior distributions generated from an additional 1000,000 iterations, thinned to 1000 samples. Convergence was confirmed using the Geweke diagnostic [26].

Findings

We identified high levels of spatial variation in the probability of IHD occurrence, which led us to examine each of the associated risk factors. For instance, Figure 3 below shows the smoothed probability of IHD incidence for each SLA stratified by age and gender. In general, the probability of being admitted with IHD for males and females between the ages of 50-54 is greater in outer suburban areas than in the inner-suburbs of Brisbane at the same time suggesting that the outlying spatial clusters are more noticeable.

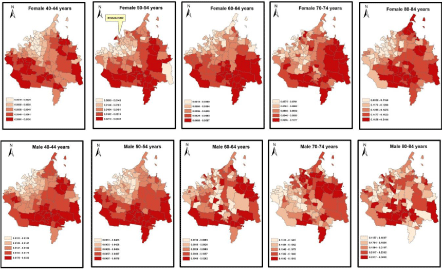
Figure 3: The Bayesian smoothed probability of IHD for each SLA stratified by age group and gender.

    
    
    Figure 3:  The Bayesian smoothed probability of IHD for each SLA stratified by age group and gender.

Urban form was only weakly associated with the incidence of IHD (Table 3). There was no urban form categories associated with consistently high or low incidence of IHD across age and sex categories. Few other covariates had statistically significant effects on the incidence of IHD, and covariate effects were highly inconsistent between age and sex categories (Tables 4 & 5).

Table 3: Univariable and multivariable results for all urban form measures.




  
    Measure
    Model
    F40
    F50
    F60
    F70
    F80
    M40
    M50
    M60
    M70
    M80
  
  
    URB1
     
    1:00
    1:00
    1:00
    1:00
    1:00
    1:00
    1:00
    1:00
    1:00
    1:00
  
  
    URB2
       
    Uni
    0.59 (0.10 to 4.61)
    1.14 (0.44 to 3.63)
    1.27 (0.62 to 2.8)
    1.57 (0.69 to 4.48)
    0.99 (0.53 to 1.98)
    1.4 (0.52 to 4.66)
    0.76 (0.42 to 1.43)
    0.66 (0.43 to 0.96)
    1.21 (0.69 to 2.14)
    1 (1 to 1)
  
  
    Multi
    0.14 (0.01 to 1.87)
    1.01 (0.29 to 4.04)
    1.04 (0.44 to 2.66)
    1.46 (0.55 to 4.4)
    0.81 (0.36 to 1.88)
    1.05 (0.35 to 3.86)
    0.6 (0.32 to 1.19)
    0.6 (0.34 to 1.11)
    1.35 (0.67 to 2.89)
    0.66 (0.3 to 1.4)
  
  
    URB3
       
    Uni
    0.85 (0.26 to 6.40)
    1.18 (0.51 to 3.16)
    1.18 (0.66 to 2.44)
    1.51 (0.71 to 3.86)
    0.93 (0.54 to 1.77)
    1.38 (0.58 to 4.42)
    0.9 (0.57 to 1.57)
    0.68 (0.5 to 0.98)
    1.26 (0.78 to 2.1)
    0.55 (0.2 to 1.6)
  
  
    Multi
    0.23 (0.03 to 2.62)
    1.06 (0.39 to 3.98)
    1.01 (0.44 to 2.35)
    1.33 (0.52 to 3.59)
    0.73 (0.36 to 1.58)
    0.94 (0.36 to 3.23)
    0.67 (0.38 to 1.21)
    0.6 (0.38 to 0.99)
    1.43 (0.77 to 2.72)
    0.69 (0.36 to 1.35)
  
  
    URB4
       
    Uni
    1.02 (0.31 to 6.89)
    1.56 (0.67 to 4.37)
    1.42 (0.81 to 2.95)
    1.94 (0.92 to 5.08)
    1.06 (0.61 to 1.99)
    1.72 (0.7 to 5.71)
    1.02 (0.65 to 1.72)
    0.78 (0.56 to 1.08)
    1.22 (0.77 to 2.02)
    0.63 (0.24 to 1.76)
  
  
    Multi
    0.16 (0.02 to 1.58)
    1.01 (0.33 to 3.96)
    1.17 (0.51 to 2.85)
    1.78 (0.67 to 4.79)
    0.69 (0.33 to 1.54)
    1.11 (0.41 to 3.65)
    0.66 (0.36 to 1.18)
    0.66 (0.39 to 1.14)
    1.38 (0.71 to 2.67)
    0.76 (0.4 to 1.49)
  
  
    URB5
       
    Uni
    0.65 (0.19 to 4.59)
    1.22 (0.52 to 3.33)
    1.1 (0.63 to 2.21)
    1.53 (0.7 to 4.01)
    0.73 (0.41 to 1.36)
    1.2 (0.5 to 3.86)
    0.86 (0.54 to 1.49)
    0.65 (0.47 to 0.92)
    1.19 (0.74 to 2.04)
    0.67 (0.23 to 2.03)
  
  
    Multi
    0.18 (0.02 to 1.81)
    1.09 (0.40 to 3.91)
    0.98 (0.47 to 2.23)
    1.47 (0.58 to 3.97)
    0.6 (0.29 to 1.25)
    0.92 (0.35 to 3.06)
    0.68 (0.39 to 1.19)
    0.58 (0.36 to 0.94)
    1.33 (0.73 to 2.51)
    0.83 (0.44 to 1.62)
  
  
    URB6
       
    Uni
    0.6 (0.14 to 4.51)
    1.42 (0.53 to 4.08)
    1.54 (0.81 to 3.23)
    1.65 (0.73 to 4.43)
    1.43 (0.76 to 2.59)
    2.08 (0.78 to 6.99)
    1.25 (0.75 to 2.16)
    0.76 (0.52 to 1.14)
    0.98 (0.6 to 1.76)
    0.76 (0.28 to 2.11)
  
  
    Multi
    0.16 (0.01 to 1.99)
    0.88 (0.27 to 3.8)
    1.13 (0.46 to 2.76)
    1.53 (0.56 to 4.5)
    0.96 (0.42 to 2.32)
    1.28 (0.45 to 4.91)
    0.84 (0.42 to 1.58)
    0.64 (0.36 to 1.12)
    1.08 (0.56 to 2.17)
    0.82 (0.39 to 1.68)



Table 3:  Univariable and multivariable results for all urban form measures.

Table 4: Demographic groups and their associated covariate estimates that were found to be statistically significant.




  
    Demographic group
    Covariate
    Odds Ratio
      (95% credible interval)
  
  
    Female 40-44 years
    WLK4^a
    0.52 (0.34 to 0.77)
  
  
    Female 50-54 years
    SES5^b
      DISPUB (distance to public hospitals)
    0.70 (0.52 to 0.98)
      0.97 (0.94, to 0.99)
  
  
    Female 60-64 years
    WLK5^a
    0.58 (0.42 to 0.78)
  
  
    Female 80-84 years
    SES5^b
      WLK5^a
    0.69 (0.54 to 0.90)
      0.73 (0.59 to 0.90)
  
  
    Male 40-44 years
    WLK4^a
      WLK5^a
    0.77 (0.62 to 0.94)
      0.59 (0.40 to 0.85)
  
  
    Male 50-54 years
    WLK5^a
    0.75 (0.59 to 0.95)
  
  
    Male 60-64 years
    URB2^c(Corridor City)
       
    0.66 (0.43 to 0.96)
       
  
  
    Male 80-84 years
    WLK1^a
      WLK2^a
      WLK4^a
    0.68 (0.51 to 0.87)
      0.80 (0.65 to 0.98)
      0.80 (0.69 to 0.94)
  
  
    ^aRelative    to WLK3 (reference category for walkability).
      ^bRelative    to SES3 (reference category for socioeconomic status).
      ^cRelative    to URB1 (reference category for urban form).



Table 4:  Demographic groups and their associated covariate estimates that were found to be statistically significant.

Table 5: Covariate effects for univariable and multivariable models, for all demographic categories.




  
    a
    Model
    F40
    F50
    F60
    F70
    F80
    M40
    M50
    M60
    M70
    M80
  
  
    URB1
    Uni
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    URB1
    Multi
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    URB2
    Uni
    0.59 (0.1 to 4.61)
    1.14 (0.44 to 3.63)
    1.27 (0.62 to 2.8)
    1.57 (0.69 to 4.48)
    0.99 (0.53 to 1.98)
    1.4 (0.52 to 4.66)
    0.76 (0.42 to 1.43)
    0.66 (0.43 to 0.96)
    1.21 (0.69 to 2.14)
    0.66 (0.3 to 1.4)
  
  
    URB2
    Multi
    0.14 (0.01 to 1.87)
    1.01 (0.29 to 4.04)
    1.04 (0.44 to 2.66)
    1.46 (0.55 to 4.4)
    0.81 (0.36 to 1.88)
    1.05 (0.35 to 3.86)
    0.6 (0.32 to 1.19)
    0.6 (0.34 to 1.11)
    1.35 (0.67 to 2.89)
    0.55 (0.2 to 1.6)
  
  
    URB3
    Uni
    0.85 (0.26 to 6.4)
    1.18 (0.51 to 3.16)
    1.18 (0.66 to 2.44)
    1.51 (0.71 to 3.86)
    0.93 (0.54 to 1.77)
    1.38 (0.58 to 4.42)
    0.9 (0.57 to 1.57)
    0.68 (0.5 to 0.98)
    1.26 (0.78 to 2.1)
    0.69 (0.36 to 1.35)
  
  
    URB3
    Multi
    0.23 (0.03 to 2.62)
    1.06 (0.39 to 3.98)
    1.01 (0.44 to 2.35)
    1.33 (0.52 to 3.59)
    0.73 (0.36 to 1.58)
    0.94 (0.36 to 3.23)
    0.67 (0.38 to 1.21)
    0.6 (0.38 to 0.99)
    1.43 (0.77 to 2.72)
    0.63 (0.24 to 1.76)
  
  
    URB4
    Uni
    1.02 (0.31 to 6.89)
    1.56 (0.67 to 4.37)
    1.42 (0.81 to 2.95)
    1.94 (0.92 to 5.08)
    1.06 (0.61 to 1.99)
    1.72 (0.7 to 5.71)
    1.02 (0.65 to 1.72)
    0.78 (0.56 to 1.08)
    1.22 (0.77 to 2.02)
    0.76 (0.4 to 1.49)
  
  
    URB4
    Multi
    0.16 (0.02 to 1.58)
    1.01 (0.33 to 3.96)
    1.17 (0.51 to 2.85)
    1.78 (0.67 to 4.79)
    0.69 (0.33 to 1.54)
    1.11 (0.41 to 3.65)
    0.66 (0.36 to 1.18)
    0.66 (0.39 to 1.14)
    1.38 (0.71 to 2.67)
    0.67 (0.23 to 2.03)
  
  
    URB5
    Uni
    0.65 (0.19 to 4.59)
    1.22 (0.52 to 3.33)
    1.1 (0.63 to 2.21)
    1.53 (0.7 to 4.01)
    0.73 (0.41 to 1.36)
    1.2 (0.5 to 3.86)
    0.86 (0.54 to 1.49)
    0.65 (0.47 to 0.92)
    1.19 (0.74 to 2.04)
    0.83 (0.44 to 1.62)
  
  
    URB5
    Multi
    0.18 (0.02 to 1.81)
    1.09 (0.4 to 3.91)
    0.98 (0.47 to 2.23)
    1.47 (0.58 to 3.97)
    0.6 (0.29 to 1.25)
    0.92 (0.35 to 3.06)
    0.68 (0.39 to 1.19)
    0.58 (0.36 to 0.94)
    1.33 (0.73 to 2.51)
    0.76 (0.28 to 2.11)
  
  
    URB6
    Uni
    0.6 (0.14 to 4.51)
    1.42 (0.53 to 4.08)
    1.54 (0.81 to 3.23)
    1.65 (0.73 to 4.43)
    1.43 (0.76 to 2.59)
    2.08 (0.78 to 6.99)
    1.25 (0.75 to 2.16)
    0.76 (0.52 to 1.14)
    0.98 (0.6 to 1.76)
    0.82 (0.39 to 1.68)
  
  
    URB6
    Multi
    0.16 (0.01 to 1.99)
    0.88 (0.27 to 3.8)
    1.13 (0.46 to 2.76)
    1.53 (0.56 to 4.5)
    0.96 (0.42 to 2.32)
    1.28 (0.45 to 4.91)
    0.84 (0.42 to 1.58)
    0.64 (0.36 to 1.12)
    1.08 (0.56 to 2.17)
    0.98 (0.34 to 3.39)
  
  
    SES1
    Uni
    1.52 (0.81 to 2.8)
    1.58 (1.1 to 2.2)
    1.39 (1.06 to 1.87)
    1.2 (0.91 to 1.56)
    0.94 (0.7 to 1.29)
    1.8 (1.29 to 2.61)
    1.36 (1.1 to 1.72)
    1.06 (0.87 to 1.3)
    1.28 (1 to 1.64)
    0.87 (0.65 to 1.19)
  
  
    SES1
    Multi
    1.42 (0.59 to 3.42)
    1.57 (0.99 to 2.53)
    1.35 (0.96 to 1.92)
    1.2 (0.82 to 1.79)
    0.87 (0.6 to 1.34)
    1.8 (1.22 to 2.72)
    1.29 (0.97 to 1.69)
    1.03 (0.77 to 1.33)
    1.3 (0.95 to 1.78)
    0.77 (0.45 to 1.27)
  
  
    SES2
    Uni
    1.89 (0.82 to 4.02)
    1.25 (0.8 to 1.98)
    1.46 (1.01 to 2.03)
    1.08 (0.76 to 1.54)
    0.9 (0.63 to 1.25)
    1.29 (0.77 to 2.06)
    1.32 (0.97 to 1.76)
    1.17 (0.92 to 1.51)
    1.39 (1.02 to 1.87)
    0.96 (0.68 to 1.32)
  
  
    SES2
    Multi
    1.71 (0.55 to 5.08)
    1.32 (0.7 to 2.55)
    1.54 (1 to 2.33)
    1.21 (0.78 to 1.89)
    0.92 (0.58 to 1.5)
    1.42 (0.8 to 2.43)
    1.3 (0.93 to 1.85)
    1.23 (0.87 to 1.71)
    1.43 (0.99 to 2.13)
    1.17 (0.7 to 2.12)
  
  
    SES3
    Uni
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    SES3
    Multi
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    SES4
    Uni
    1.15 (0.71 to 1.99)
    0.94 (0.7 to 1.27)
    0.98 (0.76 to 1.24)
    1.05 (0.82 to 1.33)
    0.87 (0.7 to 1.11)
    0.98 (0.73 to 1.34)
    0.94 (0.78 to 1.15)
    0.9 (0.77 to 1.07)
    1.19 (0.97 to 1.48)
    0.77 (0.62 to 0.98)
  
  
    SES4
    Multi
    1.17 (0.56 to 2.56)
    0.96 (0.61 to 1.45)
    1.01 (0.72 to 1.39)
    1.07 (0.78 to 1.49)
    1.11 (0.82 to 1.54)
    1.07 (0.77 to 1.55)
    0.99 (0.78 to 1.26)
    0.86 (0.69 to 1.09)
    1.19 (0.91 to 1.58)
    0.79 (0.52 to 1.25)
  
  
    SES5
    Uni
    0.67 (0.38 to 1.24)
    0.7 (0.52 to 0.98)
    0.86 (0.67 to 1.11)
    0.96 (0.75 to 1.23)
    0.7 (0.55 to 0.91)
    0.78 (0.57 to 1.12)
    0.83 (0.69 to 1.03)
    0.86 (0.73 to 1.02)
    1.24 (0.99 to 1.55)
    0.93 (0.74 to 1.22)
  
  
    SES5
    Multi
    0.52 (0.21 to 1.24)
    0.71 (0.45 to 1.11)
    0.95 (0.67 to 1.33)
    1.09 (0.77 to 1.57)
    0.92 (0.69 to 1.32)
    0.89 (0.62 to 1.37)
    0.84 (0.65 to 1.08)
    0.84 (0.66 to 1.08)
    1.26 (0.95 to 1.69)
    1.03 (0.65 to 1.67)
  
  
    DISPUB
    Uni
    1 (0.96 to 1.05)
    0.97 (0.95 to 1)
    0.99 (0.97 to 1.01)
    1 (0.98 to 1.02)
    1 (0.98 to 1.02)
    1 (0.97 to 1.02)
    1.01 (0.99 to 1.02)
    1 (0.99 to 1.01)
    1 (0.98 to 1.02)
    0.98 (0.96 to 1)
  
  
    DISPUB
    Multi
    0.97 (0.88 to 1.06)
    0.98 (0.94 to 1.03)
    0.99 (0.96 to 1.02)
    1.01 (0.98 to 1.05)
    0.98 (0.95 to 1.02)
    1.01 (0.97 to 1.05)
    1 (0.98 to 1.03)
    1.01 (0.98 to 1.03)
    1 (0.98 to 1.04)
    0.99 (0.94 to 1.04)
  
  
    DISPRV
    Uni
    1.02 (1 to 1.05)
    1.03 (1.01 to 1.04)
    1.02 (1.01 to 1.03)
    1.01 (0.99 to 1.02)
    1.03 (1.02 to 1.04)
    1.02 (1.01 to 1.04)
    1.01 (1.01 to 1.03)
    1.01 (1 to 1.01)
    1 (0.99 to 1.01)
    1.01 (1 to 1.02)
  
  
    DISPRV
    Multi
    1.01 (0.94 to 1.08)
    1 (0.96 to 1.03)
    1 (0.97 to 1.02)
    1 (0.97 to 1.02)
    1.03 (1 to 1.05)
    0.99 (0.97 to 1.02)
    1 (0.98 to 1.02)
    0.99 (0.98 to 1.01)
    1 (0.98 to 1.02)
    1.02 (0.99 to 1.07)
  
  
    WLK1
    Uni
    1.03 (0.62 to 1.55)
    0.91 (0.69 to 1.19)
    0.94 (0.72 to 1.16)
    0.87 (0.67 to 1.13)
    1.16 (0.92 to 1.53)
    0.78 (0.56 to 1.03)
    1.09 (0.92 to 1.3)
    0.97 (0.83 to 1.12)
    0.9 (0.75 to 1.09)
    0.68 (0.52 to 0.88)
  
  
    WLK1
    Multi
    1.34 (0.63 to 2.88)
    1.14 (0.75 to 1.72)
    0.93 (0.66 to 1.32)
    0.76 (0.53 to 1.09)
    1.13 (0.79 to 1.58)
    0.81 (0.58 to 1.19)
    1.1 (0.87 to 1.38)
    0.93 (0.75 to 1.17)
    0.89 (0.68 to 1.17)
    0.5 (0.31 to 0.77)
  
  
    WLK2
    Uni
    0.94 (0.6 to 1.48)
    0.88 (0.66 to 1.16)
    1 (0.81 to 1.2)
    0.87 (0.71 to 1.05)
    1.03 (0.84 to 1.26)
    1.05 (0.81 to 1.35)
    0.99 (0.83 to 1.18)
    0.95 (0.81 to 1.1)
    0.99 (0.84 to 1.17)
    0.8 (0.65 to 0.98)
  
  
    WLK2
    Multi
    0.86 (0.45 to 1.63)
    0.83 (0.56 to 1.17)
    0.95 (0.71 to 1.25)
    0.83 (0.62 to 1.1)
    0.98 (0.71 to 1.29)
    1.09 (0.8 to 1.47)
    0.96 (0.8 to 1.18)
    0.91 (0.74 to 1.12)
    0.97 (0.78 to 1.21)
    0.59 (0.41 to 0.87)
  
  
    WLK3
    Uni
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    WLK3
    Multi
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
    1 (1 to 1)
  
  
    WLK4
    Uni
    0.52 (0.35 to 0.77)
    0.84 (0.68 to 1.02)
    0.96 (0.82 to 1.13)
    0.89 (0.77 to 1.05)
    0.91 (0.78 to 1.07)
    0.78 (0.62 to 0.94)
    0.93 (0.81 to 1.06)
    0.92 (0.82 to 1.03)
    0.93 (0.82 to 1.06)
    0.81 (0.69 to 0.94)
  
  
    WLK4
    Multi
    0.59 (0.33 to 1.11)
    0.92 (0.68 to 1.25)
    0.98 (0.8 to 1.21)
    0.94 (0.75 to 1.18)
    0.9 (0.72 to 1.11)
    0.82 (0.64 to 1.06)
    0.92 (0.77 to 1.08)
    0.94 (0.79 to 1.1)
    0.98 (0.82 to 1.18)
    0.76 (0.57 to 1)
  
  
    WLK5
    Uni
    0.57 (0.29 to 1.05)
    0.76 (0.54 to 1.07)
    0.59 (0.42 to 0.79)
    0.87 (0.68 to 1.12)
    0.74 (0.6 to 0.91)
    0.6 (0.41 to 0.85)
    0.75 (0.6 to 0.96)
    1.01 (0.85 to 1.18)
    1.03 (0.85 to 1.24)
    0.86 (0.67 to 1.11)
  
  
    WLK5
    Multi
    0.71 (0.25 to 1.94)
    0.77 (0.45 to 1.3)
    0.64 (0.42 to 0.9)
    0.87 (0.6 to 1.25)
    0.77 (0.54 to 1.07)
    0.72 (0.47 to 1.09)
    0.81 (0.62 to 1.08)
    1.08 (0.84 to 1.41)
    1.04 (0.79 to 1.41)
    0.85 (0.54 to 1.35)



Table 5:  Covariate effects for univariable and multivariable models, for all demographic categories.

There were generally strong patterns of residual spatial variation after accounting for the combined effects of urban form, ethnicity, socioeconomic status, walk ability and distance to local hospitals. Figure 4 shows the odds ratios (residual variation) from the fully adjusted model versus the odds ratios from random effects model (model that did account for the covariates) [bottom]. The findings suggest that after accounting for the covariates, the inter quartile difference between the demographic categories decreases (smaller inter quartile range). For instance, before accounting for the covariates within the Male 50-54 age group (Odds of IHD hospitalisation), the inter quartile ranges were between 0.89 to 1.14. After accounting for the covariates, the inter quartile ranges for the same groups were between 0.97 to 1.05, see also (Figure 5). We can therefore surmise from these findings that after accounting for the covariates the inter quartile differences between demographic groups were predominantly more noticeable for male’s between50-54 and 40-44 years of age, spatial pattern identified the odds of IHD hospitalisations for 60-64 year old males were significantly greater in outer suburban areas compared to the inner-suburbs of Brisbane.

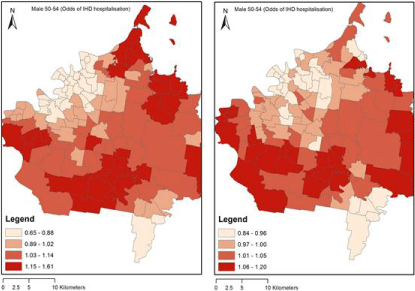
Figure 4: Odds ratios from random effects model (no covariates) [top], and fully-adjusted model (residual variation) [bottom].

    
    
    Figure 4:  Odds ratios from random effects model (no covariates) [top], and fully-adjusted model (residual variation) [bottom].

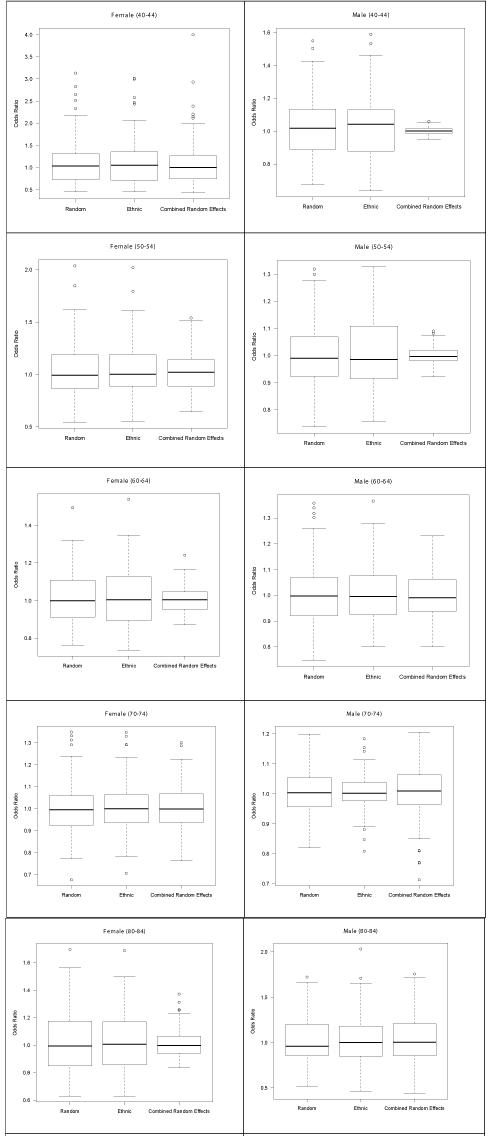
Figure 5: Box plots diagram that shows the interquartile range of odds ratios across the age and sex categories.

    
    
    Figure 5:  Box plots diagram that shows the interquartile range of odds ratios across the age and sex categories.

Discussion, Limitations and Future Research

A result of urban or semi urban characteristics of our area of interest. This however, remains to be investigated further. In this study, the principal aim was to test for a relationship between urban form and IHD; the results suggest that urban form was not a strong predictor of IHD. In fact, the covariates did little to explain the variation between SLAs, with the exception of 60-64 year old men demographic category. Even with this finding, albeit marginal, there was little additional evidence of an effect of urban form on the incidence of ischemic heart disease. It may be that similar to past attempts to identify the impacts of urban form, these differences are very small or it may be that there better ways to measure urban form. For instance, de Andrade et al. [18]. Suggest that the high mortality rate of IHD within regional areas were dependent on the distance between each city and their reference interventional cardiology centre, which implies that distance to hospital may be a potential confounder. However, in our study we did not find strong evidence pertaining to distance, which may be as strong patterns of spatial variation in IHD have been observed in the study. Spatial variation has been tested after taking multiple risk factors into account. There were generally strong patterns of residual spatial variation in IHD after taking into account the covariates. For example, patterns of spatial variation in the rates of IHD can be seen in women aged 40-44 years of age with higher incidences of hospitalisation on either side of the multi-node corridor. However with the increase in age, women in the study area were more likely to be hospitalised in the fringe city region than the dispersed city category, reasons for that were left unanswered.

The effects of other covariates were generally weak and inconsistent between demographic categories. For instance, different demographic categories showed different amounts of spatial variation and different relationships within the covariates. It appeared that after controlling for socioeconomic status and other covariates, the urban form variables were not associated with strong effects of IHD hospitalisation. The improved model simply did not reveal a sufficient difference.

Several limitations must be considered in this study. In general, the study did not reveal why IHD may have a relationship to urban form. It was found that the effect of most covariates was generally weak, but there were some effects that varied between demographic categories, which may require further investigation. Therefore, we were not able to make any firm conclusions about why or whether a particular set of covariates was important for a particular demographic group. Also, for some demographic groups, there was a decrease in residual variation (e.g., male 50-54 and male 40-44), after including all covariates in the model. This is an important finding, since it creates an opportunity for further investigation focused on these two age groups. The potential of limitations of geographic scale which constrained the study to an aggregated SLA level as opposed to the more detailed SA1 (statistical Area Level 1), may have been more suitable scale and may have yielded higher spatial resolution. Other limitations that were found in our dataset were those related to the type of datasets being assembled and some of the measures used in the covariates. With regards to some of the measures used in the covariates, the Walk Score data that was used ignores topography, urban design measures (other than those that affect networks and distances such as ‘connectivity’ etc.) and in Australia has a reduced level of information than in US cities, which could have limited its utility. Also, the fact that we used centroids to represent a large area of SLAs rather than specific location reduces its reliability as SLAs can vary spatially in its walk ability level, especially if they are large areas. In Summary, this study was pioneering in its nature and perhaps is one of the first attempts in the literature to test the relationship between urban form and IHD and health measures in general. More research will be required to address the unanswered questions raised (e.g., better way to measure urban form or the findings associated with the 40-44, 50-54 male group) in this study and may constitute a new avenue for future studies in this domain.

Acknowledgment

We thank Dr Geoff Morgan (University of Sydney) and Dr Rosemary Wyber (Telethon Kids Institute) for initial discussions about types of heart disease to focus on. We also would like to thank the following organisations who made this study possible:

Queensland Health Statistics unit
Queensland Health
Griffith Health Institute; Griffith University

References

Download PDF

Citation: Gudes O, Ball SJ, Dur F, Burke M and Varhol R. The Association between Urban Form and Ischemic Heart Disease: Evidence from Brisbane, Australia. Austin J Public Health Epidemiol. 2015;2(1): 1014. ISSN : 2381-9014

Instruction for Authors

Submit Your Article