Review Article
Austin Stat. 2014;1(1): 7.
Risk Segmentation Using Bayesian Quantile Regression with Natural Cubic Splines
Xia M*
Department of Statistics, Northern Illinois University, USA
*Corresponding author: :Xia M, Division of Statistics, Northern Illinois University, 300 Normal Road, DeKalb, IL 60115, USA
Received: May 29, 2014; Accepted: July 11, 2014; Published: July 16, 2014
Abstract
An insurance claims department is often interested in obtaining the possible distribution of a claim for the purpose of risk management. Information such as the probability that a claim will exceed a certain amount is helpful for matching the claim complexity with the specialty of claim adjusters. Using information available on the claim and the parties involved, we propose a Bayesian quantile regression model for the purpose of risk identification and segmentation in the claims department. Natural cubic splines are used in order to estimate a smooth relationship between the expected quantiles and continuous explanatory variables such as the age of the claimant. A case study is conducted using the Medical Large Claims Experience Study data from the Society of Actuaries. For the claimant age factor that we study, we observe that the high-risk groups, such as the infants and elderly, exhibit a much higher risk in terms of high quantiles (such as the 99% and 99.5% percentiles) than that is revealed by the mean or the median. Particularly for the claims data where there are various characteristics available on the claimant and other parties involved, our model may reveal helpful information on the possible extremal risk that may be under looked in traditional claims modeling.
Keywords: Risk segmentation; Bayesian quantile regression; Natural cubic splines; Markov chain Monte Carlo; predictive modeling of claims
Introduction
Insurance companies are often interested in assessing the risks associated with an insurance claim before it is finally settled. For the financial industry, a high risk not only means a high average amount, but also the possibility of an extremely large loss. For example, the claims department may be interested in the expected quantiles of the claim distribution (e.g., what is the probability that the claim will exceed a certain amount), once information is available on the claim and the parties involved. This information can be used to match the claim complexity with the specialty and experience of the claim adjusters. Therefore it is helpful to model different quantiles of the loss distribution, given certain characteristics of the claim and the parties involved.
Regression methods have been proven to be useful for the predictive modeling of insurance claims, particularly when there is information available on the claim characteristics. Proposed in earlier papers such as [1], generalized linear models (GLMs) have now become popular in nonlife rate-making and reserving. In the recent decades, more sophisticated regression models such as the generalized additive models (GAMs, [2]. Bayesian GAMs [3], generalized linear mixed models [4], quantile regression [5] have been proposed for rate-making and stochastic reserving. In recent papers such as [6,7] Bayesian generalized linear models were used to predict the outstanding claims for different combinations of loss and accident years. The earlier works on claims and reserve modeling, however, only involves regression on location parameters such as the mean and median of the loss distribution. In this paper, we propose to use Bayesian quantile regression [8] with natural cubic splines [9-13] for the purpose of risk identification and segmentation in the claims department. Quantile regression [14] has become popular in predictive modeling in econometrics and social science, as it provides a more complete picture of the distribution. Recent developments in quantile regression have been focusing on regularization [15-17]. Under the Bayesian framework [18], developed Gibbs samplers for Bayesian regularized quantile regression with lasso [19] group lasso [20] and elastic net penalties [21-22] improved the work of [18] by allowing different penalization parameters for different regression coefficients. Bayesian methods have the advantage of incorporating expert knowledge through priors. In addition, posteriors samples from Markov chain Monte Carlo (MCMC) simulations enable statistical inference on the estimated coefficients as well as regression lines with little extra computational cost.
For the Bayesian quantile regression model we propose for risk segmentation, we will conduct a case study using the Medical Large Claims Experience Study (MLCES) data from the Society of Actuaries (SOA). Natural cubic splines [9,10] will be used for obtaining a smooth relationship between the fitted quantiles and the age of the claimant. For model fitting, we will try using both the Bayesian quantile regression method [8], and non Bayesian methods such as those from [15,23,24] For the claimant age factor that we study, we observe that the high-risk groups, such as the infants and elderly, exhibit a much higher risk in terms of high quantiles (such as 99% and 99.5%) than that is revealed by the mean or the median. Particularly for the claims data where there are various characteristics available on the claim and the parties involved, our model may reveal helpful information on the possible extremal risk that may be under looked in traditional claims predictive modeling. Our case study confirms that Bayesian quantile regression may be a useful tool for risk identification and segmentation in the claims department.
The rest of the paper is organized as follows. In Section 2, we will introduce relevant methodologies such as quantile regression, Bayesian quantile regression and natural cubic splines. In Section 3, we will conduct a case study using the MLCES data from SOA. Section 4 concludes the paper.
Methodologies
Quantile regression
The concept of quantile regression was first introduced by [14]. While linear regression focuses on conditional expectations, quantile regression is for modeling conditional quantiles given certain explanatory variables. Denote y1, y2,..., yn as n observations of the response variable under concern, and x1, x2,..., xn as the vectors of explanatory variables of length k. For 0 < p < 1, the linear regression model for the path quantile is given by
Where Qp(yi/xi) is the inverse cumulative distribution function of yi given xi evaluated at the probability p, and β is a vector of coefficients for the k explanatory variables in xi. Here we will discuss the methods based on a linear relationship between the quantiles of the response and the explanatory variables, although the methods may be extended for non-linear relationships.
While the coefficients of the ordinary linear regression are estimated by minimizing the sum of squared errors, estimates of the quantile regression coefficients β (ρ) are called the pth regression quantile, and are obtained by minimizing
where ρp(·) is the check loss function defined by
which places asymmetric weights on positive and negative residuals.
In [23], the regression quantiles (i.e., coefficients) were estimated using a modified simplex algorithm proposed by [25, 23] noted that the computational cost of the algorithm can increase dramatically when the sample size and the number of parameters increase. Hence, in [26] the authors proposed interior point methods with a new statistical preprocessing approach for l1-type problems. These new algorithms increased the computational speed by 10 to 100-fold. Interested readers may refer to the original papers for detailed information on the algorithms. Statistical inference on the regression quantiles is usually achieved by re sampling methods such as bootstrapping. The re sampling methods for quantile regression were discussed in papers such as [15,27]. Other methods for statistical inference in quantile regression include the inversion of rank test proposed by [28] and the direct and studentization methods by [29]. In actuarial science [5], proposed to use quantile regression for the purpose of nonlife rate-making [5]. Took advantage of the robustness of the fitted quantiles in the presence of outliers. To our knowledge, however, little research seems to have been con- ducted in the actuarial literature to make use of the capability of quantile regression in revealing comprehensive distributional characteristics including both the location and scale.
Quantile regression with penalty
In order to avoid over-fitting and to provide regularization in variable estimation, variable selection by penalized likelihood has gained much attention under the regression context. For quantile regression [15], was the first paper that introduced penalty functions to shrink the estimates of random effects for longitudinal data. The penalized version of Equation (2) is given by
Where λ is the regularization parameter (i.e., a tuning parameter), and J(·) is the penalty function.
In [15,17], the LASSO penalty [19] was used for regularization and variable selection. The LASSO quantile regression [15] is estimated by minimizing
where λ is nonnegative, and is the l1 penalty which shrinks the regression coefficients to zero as λ increases.
Another well-known penalized quantile regression model is the SCAD quantile regression pro-posed by [24]. According to Fan and [30] the SCAD penalty possesses the oracle properties that the LASSO does not have. The SCAD quantile regression coefficients are estimated by minimizing
where the SCAD penalty pλ(·) is defined based on its first derivative and is symmetric around zero.
For θ> 0, the first derivative of the SCAD penalty is given by
where a > 2 is a tuning parameter. The SCAD penalty has a form similar to the LASSO penalty around zero, but it places a uniform penalty on large coefficients in order to achieve the unbiasedness for penalized estimators.
In addition to the SCAD penalty, [24] proposed the adaptive LASSO penalty for quantile regression. The adaptive LASSO is a generalization of the LASSO penalty which allows adaptive weights (i.e., different weights) for different regression coefficients. According to [31] the adaptive LASSO also posses the oracle properties. Details of adaptive LASSO quantile regression can be found in [24].
Bayesian quantile regression
In [8] the authors introduced Bayesian quantile regression using a likelihood function based on the asymmetric Laplace distribution. This is based on the property that the minimization of Equation (2) is equivalent to the maximization of the likelihood function for in-dependently distributed asymmetric Laplace distributions. The probability density function of an asymmetric Laplace distribution is given by
where 0 < p < 1 and ρp(_) is the check loss function defined in Equation (2). Except for p = 1/2, the density in Equation (7) is asymmetric.
After introducing a location parameter μ and a scale parameter s into Equation (7), we may obtain a generalization of the density as
Under the assumptions of the asymmetric Laplace distribution and a link function as the inverse cumulative distribution, one may estimate the coefficients of quantile regression by maximizing the likelihood similar to parameter estimation in the case of a generalized linear model (GLM). Denote as the distribution function of the response variables yi, and the GLM link function as . Regardless of the original distribution of the data, inference can be made if we assume that for any 0 < p < 1,
where is the inverse cumulative distribution function defined earlier in Subsection 2.1.For the purpose of Bayesian analysis, we denote π(β) as the priors for the pth regression quantiles (i.e., coefficients), y = (y1, y2,...,yn) as the n observations of the response variable, and as the conditional distribution of the response variable based on the asymmetric Laplace distribution.
That is,
Bayesian inference can be made based on the posterior distribution given by
Although a conjugate prior is not available for exact analysis, Markov chain Monte Carlo (MCMC) techniques may be used to obtain posterior samples of the regression coefficients for the purpose of statistical inference [8]. Demonstrated that improper priors on β will yield a proper posterior distribution. Vague or non-informative priors may be chosen to reflect lack of information, while informative priors may be specified when subject-area knowledge is available. In the case of an informative prior, the prior mean represents a guess of the regression coefficients, and the prior variance or precision indicates the uncertainty on the guess. In quantile regression, the use of MCMC enables statistical inference on the regression quantiles with little extra computational cost. Using the posterior samples from MCMC, one may construct credible intervals for the fitted quantiles, where non Bayesian methods encounters difficulties and for which re sampling methods can be computationally expensive, particularly for large insurance data.
In the recent decade, the developments of Bayesian quantile regression have had a focus on parameter regularization and variable selection. For example, [18] proposed Bayesian regularized quantile regression with lasso [19] group lasso [20] and elastic net penalties [21,18] developed Gibbs samplers for the three types of regularized quantile regression, and demonstrated that the Bayesian regularized quantile regression perform better than the non-Bayesian methods in terms of accuracy and prediction by simulation studies [22] improved the work of [18] by allowing different tuning parameters for different regression coefficients, with the performance of their method evaluated by simulations and case studies. Interested readers may refer to the original papers for details on the new methods.
Natural cubic splines
In the quantile regression model given in Equation (1), the relationship between the quantiles of the response variable and the explanatory variables is assumed to be linear. This is often not true under realistic situations. For example, in property and casualty loss modeling, the younger people and the elderly usually exhibit a higher risk in terms of potential losses (see, e.g., [32]). Another example is the vehicle age variable in auto rate-making, which has a similar pattern at the younger and older vehicle ages (see, e.g., [33]). Some natural ways to model a nonlinear relationship include polynomials and piece-wise functions. For example, the property and casualty pricing software Emblem enables actuaries to model the relationship between the expected losses and continuous rating factors using polynomials. However, for polynomials, the number of parameters grows exponentially with the order of polynomials. And the shapes of polynomials are constraint based on the order specified. Splines are piecewise polynomials with local polynomial representations. For regression purposes, fixed-knot splines are widely used for obtaining a nonlinear relationship. Splines are assumed to be continuous, and have continuous first and second derivatives at the knots, in order to provide a smooth relationship. Splines can be defined based on the order of polynomials, the number of knots and their positions. Cubic splines are the lowest-order splines with the knot-discontinuity that is undetectable by human eyes (see, e.g., Chapter 5 in [9]. In order to avoid the erratic behavior of splines at the boundaries that may cause a problem in extrapolation, we may use natural cubic splines that add the additional constraints of linearity beyond the two boundaries. For example, in[10,11] natural cubic splines were used to model the relationship between disease prevalence and medical expenditure (utilization) with sampling probabilities in order to extrapolate the disease prevalence and medical expenditure (or utilization) for hidden sub-populations in weighted sampling.
Here we present a natural cubic spline with 4 knots as an example. Denoting (x1, x2, x3, x4) as the 4 knots, the spline is defined by three cubic functions within each interval divided by the knots:
with ak, bk, ck and dk be the coefficients of the local cubic functions. At the four knots the natural cubic spline has the nice properties that
For splines, one may perform a linear basis expansion for the convenience and simplicity of model implementation. A natural cubic spline with K knots can be represented by K basis functions h1(x); h2(x),...,hK(x). The basic functions satisfy the property that
where α1; α2,...,αK are the coefficients. Using the basic functions from basis expansion, linear models can be conveniently fitted to the basic functions, which results in natural cubic splines in providing a smooth and flexible relationship.
Case Study on MLCES Data
Data
For demonstration purposes, we will conduct a case study using the Medical Large Claims Experience Study (MLCES) data from the Society of Actuaries (SOA). The 1999 file [34] that we use has 1,591,738 records, containing the total paid charges as well as explanatory variables such as the age, the gender and the major disease diagnosis of the claimant. Here we chose the age of the claimant as a factor that may impact the distribution of the claims. The reason why we chose age is because insurance claims usually exhibit a declining trend at the younger ages and an increasing trend at the older years [32]. It would be interesting to see how the distribution (including the upper tail that is of particular interest to the insurance industry) varies by the age of the claimant. In order to obtain homogeneous data with a reasonable sample size, we only include claims with a major diagnosis of respiratory system problems. The subset we use contains 165,786 records and one specific explanatory variable for illustration purposes, although in reality we may have numerous variables available on the claim to be used as predictors in our quantile regression model. For example, for auto bodily injury claims, the claims department may have various information on the claimant, the insured, the injury conditions, and the legal firm involved, before the claim is finally settled. The information may be used to predict the quantiles of the claim, using a model fitted from historical data. Based on the estimated quantiles, the claims department may be able to make decisions on assigning adjusters or taking risk management measures if necessary.
Exploratory analysis
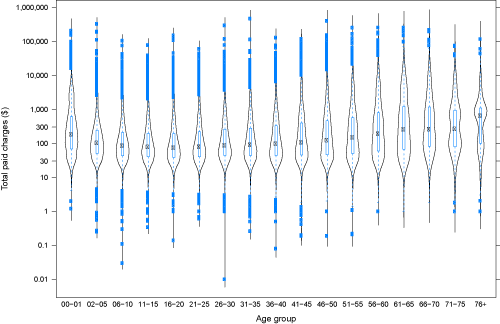
Due to the heavy-tailed property of the claim data, we transform the amount into the logarithmic scale in order to obtain a good visualization of the distribution, particularly at the body of the claim distribution. The age of the claimant for the MLCES data varies from 0 to 105, with the sample size decreasing for older ages. As our dataset provides an adequately large sample size, it would be interesting to study how the distributions of claims vary by the age of the claimant. In Figure 1, we present the distribution of log10 (total paid charges) in violin plots which contains box plots as well as density curves for different age groups. From an animation density plot we created by age, we observe that the ages 0-1 have a much higher location and scale for the distribution of the claim amounts than toddler years after age 2. We divide the claimants into 5-year age groups, with the infants (age 0 and 1) and the elderly over 76 in separate groups as they exhibit different loss behaviors. After the grouping, we have ensured that the sample size (varying from 515 to 24,727) is large enough for each age group. We observe that the median and the first and third quantiles all show a declining trend at the younger ages and an increasing trend at the older years. The range of the distribution (i.e., IQR) also varies with the age of the claimant, especially obvious at the older ages. From the density curves, the older age groups have a larger spread of density at the upper tail. Some age groups such as the 71 | |75 and 76+ groups have multiple modes in the distribution, suggesting heterogeneity due to possible difference in other factors such as the relationship to the subscriber and deductibles. All of the above observations suggest a higher financial risk for claimants at younger and older ages, both in terms of the claim severity and variability.
Figure 1: Violin plot of log10(total paid charges) by age of claimant. The y-axis is in the dollar scale for better understanding of the actual amounts. The curves outside the boxplots present the kernel densities.
Bayesian quantile regression with natural cubic splines
In this section, we propose to use Bayesian quantile regression in order to obtain a more complete picture of the claim distribution by the age of the claimant. In claim practices, the model may provide the claims department with the possible distribution of the claim based on a fitted model from historical data. The information will be helpful for the claims department for matching the claim complexity with the specialty of the claim adjusters for the purpose of risk management.
Natural cubic splines are used to provide a flexible shape to capture the trend in the lower and older ages. Denote y1, y2,...,yn as the log10(total paid charges) for n medical claims, and x1, x2,..., xn as the observed age for the n claimants. For the pth quantile, the quantile regression model is given by
where h1(·), h2(·),...,hK(·) are the K basis functions for the natural cubic spline. Note that the fitted quantiles are invariant under the log and exponential transformations.
For the purpose of risk identification and segmentation at the claims department, the quantiles of 5%, Q1, Median, Q3, 95%, 99% and 99:5% are fitted on the log10(total paid charges), in order to obtain a complete picture of the loss distribution. Diffuse priors are used due to lack of information on the parameters. In particular, for the coefficients of natural cubic splines, independent normal priors with the mean of 0 and the variance of 100 are used; for the parameter s, an inverse gamma prior with a shape parameter of 0.01 and a scale parameter of 0.01 is used. Based on Figure 1, we choose the ages 0, 20, 60 and 75 as the knots for the natural cubic splines. From Figure 1, the median and quantiles seem to change smoothly except after age 60. In order to capture the change in pattern, we chose age 60 as the third knot so that a separate cubic function can be fitted for these ages. The end knot 75 was chosen such that a linear trend is assumed after the age 75 for which the sample size is much smaller. We also include an indicator about infancy (i.e., age 0 and 1) based on a preliminary analysis on the empirical quantiles. The basic functions for the natural cubic splines were obtained from the ns () function in the R package splines. For model fitting, we tried using the method proposed by [25], interior point method [23], interior point method with preprocessing [23], penalized uantile regression with the LASSO [15] and SCAD [24] penalties, and the Bayesian implementation based on the asymmetric Laplace distribution [8]. For Bayesian quantile regression, vague priors are specified to reflect our lack of information on the coefficients of natural cubic splines. Except for the penalized methods that show a slightly erratic behavior on the high quantiles (such as the 99% and 99:5% percentiles) all the other methods give very close results in terms of the fitted quantiles.
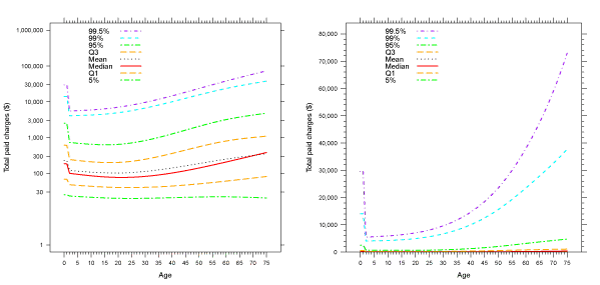
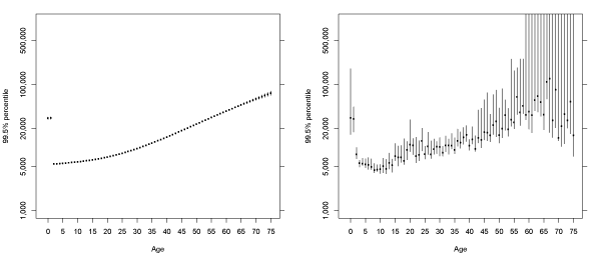
In Figure 2, we present the fitted quantiles by the age of the claimant using Bayesian quantile regression with natural cubic splines, both in the log and dollar scales. The log scale will offer us a complete picture on the body of the claim distribution, while the dollar scale shows us how large the difference it can be for the high-risk and low-risk groups in terms of high quantiles such as the 99% and 99:5% percentiles. For Bayesian quantile regression, we obtain the fitted quantiles and credible intervals based on 4000 posterior samples after discarding the first 2000. In addition, a linear regression model with natural cubic splines is fitted to the log10 (total paid charges), assuming the losses follow lognormal distributions.
Figure 2: Fitted quantiles of total paid charges by age of claimant. The left panel is in the scale of log10(total paid charges) for better display in the body of the claim distribution. The tted quantiles are from Bayesian quantile regression on log10(total paid charges), with natural cubic splines used for smoothing.
We observe that the quantiles of Q1, Median, Q3, 95%, 99% and 99:5% all have a declining trend at the younger ages, and an increasing trend at the older years. The range of the loss distribution (i.e., variability) has an obvious increase at both the younger and older ages. Based on the sharp increases in the higher quantiles, we may conclude that large losses (e.g., a claim over 10,000) are much more possible for claimants at older ages. Quantile regression offers us a complete picture of how the claim quantiles change with the age of the claimant, quantifying the earlier findings and giving us an alarm on the much higher risk of an extremely large loss for the infants and elderly people. For example, the difference in the 99:5% percentiles can be as high as 15 times between the high-risk and low-risk groups, while the difference in the median or mean is only 3 times.
Using a quantile regression model fitted from historical data, the claims department may be able to obtain the probability that a claim will exceed a certain amount, based on the claim characteristics and the parties involved. They may then use the information for risk segmentation and management (e.g., in matching the claim complexity with the specialty of the claim adjusters for better risk management, or taking other risk management initiatives if necessary). For the current data, none of pairs of fitted quantiles in Figure 2 seem to cross over. Theoretically, crossing could occur for certain datasets. In these cases, interested readers may refer to [35] for a constraint version of quantile regression that addresses the potential issue.
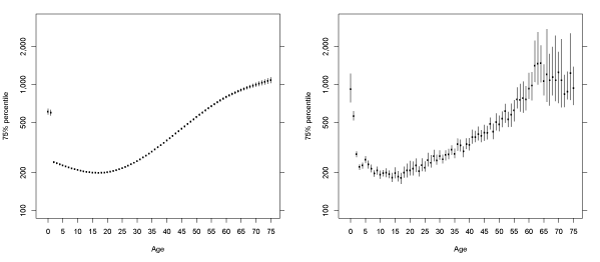
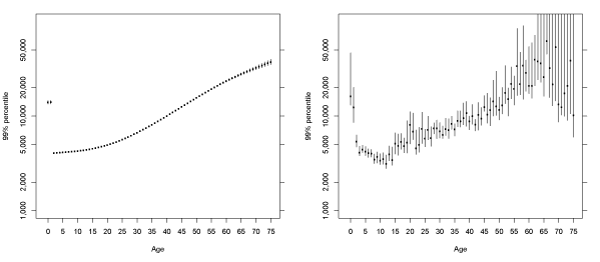
Taking advantage of the flexibility offered by MCMC in Bayesian quantile regression, we are able to obtain the 95% credible regions for the fitted quantile regression lines, under the natural cubic spline assumption. In Figure (3-7) we present the fitted quantiles with credible regions obtained from the same 4000 posterior samples used for calculating the posterior mean. The empirical quantiles and the exact 95% confidence intervals are obtained for each age and are presented for comparison purposes. From Figure (3-7), we observe that the credible intervals for the fitted quantiles from Bayesian quantile regression are very narrow comparing to those of the empirical quantiles. This is due to the fact that there are only 4 parameters for obtaining the relationships under the assumption of natural cubic splines with 4 knots, while it requires 76 parameters in order to estimate a separate quantile for each age. Particularly for younger and older ages, the confidence intervals for the empirical quantiles can be very wide, owing the small sample sizes at these ages. For the Bayesian quantile regression model with natural cubic splines, the credible intervals are very narrow due to an extremely large sample size and the smooth assumption made in the model. We note that there is only a moderate increase in the width of the credible intervals in the older and younger ages, despite their small sample sizes. For these ages, we may need to pay a special attention, as the actual increases in extremal risks may be underestimated due to the sparse data for these ages. For the high quantiles such as the 99:5% and 99% percentiles, the actual difference between the high-risk and low-risk groups may be even higher than that is revealed by our model.
Figure 3: Fitted median of log10 (total paid charges) by age of claimant. The left panel is the tted quantiles from Bayesian quantile regression, while the right panel is based on the empirical quantiles for each age. The dot in the center represents the (posterior) mean, while the line displays the 95% credible (or confidence) intervals.
Figure 4: Fitted Q3 of log10 (total paid charges) by age of claimant.
Figure 5: Fitted 95% percentiles of log10 (total paid charges) by age of claimant.
Figure 6: Fitted 99% percentiles of log10 (total paid charges) by age of claimant.
Figure 7: Fitted 99:5% percentiles of log10 (total paid charges) by age of claimant.
Concluding Remarks
In this paper, we propose to use Bayesian quantile regression with natural cubic splines for the purpose of risk identification and segmentation in the claims department. Natural cubic splines are used to provide a flexible relationship between the quantiles and continuous explanatory variables. In claims predictive modeling, such explanatory variables include the age variable that exhibits a decrease in the earlier ages and a sharp increase in the older ages [1,32]. Bayesian and MCMC techniques enable us to make statistical inference and obtain credible regions for the fitted quantiles, with little extra computational cost. Particularly in more realistic situations when there are many explanatory variables available for the predictive modeling of claims; our Bayesian regression model may be a useful tool for a comprehensive understanding of the loss distribution. In these situations, the good balance of flexibility and parsimony offered by natural cubic splines may be needed for simultaneously including many continuous variables. The examples of these variables for auto bodily injury claims include the age of the claimant, the age of the insured and the claimant, the number of years licensed for the driver and the insured, the duration of the claim, the vehicle age, the credit score of the claimant and the driver, the number of years claim free for the driver and the insured, the number of existing claims, and the income of the claimant and driver. For individual insurance companies, we may expect them to have a smaller sample size for modeling. Hence we may expect to see wider credible intervals when we include many explanatory variables into the quantile regression model. Under these situations, our Bayesian quantile regression model will provide a realistic tool for claims predictive model for the purpose of risk identification and segmentation at the claims department. In addition to the methodological benefits, predictive modeling of the claim distribution including extremes (high quantiles) may help insurance companies identify more sources of risks. For example, our case study on the MLCES data suggests that the high-risk groups such as the infants and the elderly may exhibit a much higher risk in terms of high quantiles (such as the 99:5% and 99% percentiles) than that is revealed by the location parameters such as the mean and the median. While the mean and the median only indicates a difference of 3 times, the difference in the high quantiles is revealed to be as high as 15 times between the low-risk and high-risk groups. The actual difference may ever be higher, due to possible underestimation caused by lack of data for the older ages. The extremely large losses, although with a very small possibility, may cause a severe financial impact once they occur. With the rising of the claim costs, developing comprehensive predictive models for the claims department has become an increasingly important task for risk management of insurance companies.
References
- Brockman MJ, Wright TS. Statistical motor rating: making effective use of your data. Journal of the Institute of Actuaries.1992; 119: 457-543.
- Verrall R. Claims reserving and generalised additive models. Insurance: Mathematics and Economics. 1996; 19: 31-43.
- Denuita M, Lang S. Non-life rate-making with bayesian GAMs. Insurance: Mathematics and Economics. 2004; 35: 627-647.
- Antonio K, Beirlant J. (2007). Actuarial statistics with generalized linear mixed models. Insurance: Mathematics and Economics. 2007; 40: 58-76.
- Kudryavtsev AA. Using quantile regression for rate-making. Insurance: Mathematics and Economics. 2009; 45: 296-304.
- de Alba, E. Claims reserving when there are negative values in the runoff triangle: Bayesian analysis using the three-parameter log-normal distribution. North American Actuarial Journal. 2006; 10: 45-59.
- Xia M, Scollnik D. A Bayesian stochastic reserving model accounting for zeros and negatives in loss triangle. 2014. [Under review].
- Yu K, Moyeed RA. Bayesian quantile regression. Statistics & Probability Letters. 2001; 54: 437-447.
- Hastie T, Tibshirani R, Friedman J, Franklin J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second ed. Springer, New York. 2009.
- Xia M, Gustafson P. A Bayesian method for estimating prevalence in the presence of a hidden sub-population. Statistics in Medicine. 2012; 31: 2386-2398.
- Xia M, Gustafson P. Bayesian sensitivity analyses for hidden sub-populations in weighted sampling. The Canadian Journal of Statistics. 2014. [in press].
- Hua L, Xia M. Assessing high-risk scenarios by full-range tail dependence copula. North American Actuarial Journal. 2014. [in press].
- Hua L. Tail negative dependence and its applications for aggregate loss modeling. Under review. 2014.
- Koenker R, Bassett G. Regression quantiles. Econometrica. 1978; 46: 33-50.
- Koenker R. Quantile regression for longitudinal data. Journal of Multivariate Analysis. 2004; 91: 74-89.
- Wang H, Li G, Jiang G. Robust regression shrinkage and consistent variable selection through the LAD-lasso. Journal of Business & Economic Statistics. 2007; 25: 347-355.
- Li Y, Zhu J. L1-norm quantile regression. Journal of Computational and Graphical Statistics. 2008; 17: 163-185.
- Li Q, Xi R, Lin N. Bayesian regularized quantile regression. Bayesian Analysis. 2010; 5: 533-556.
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series. 1996; 58: 267-288.
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society, Series. 2006; 68: 49-67.
- Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, Series. 2005; 67: 301-320.
- Alhamzawi R, Yu K, Benoit DF. (2012). Bayesian adaptive LASSO quantile regression. Statistical Modelling. 2012; 12: 279-297.
- Koenker R, d'Orey V. Computing regression quantiles. Applied Statistics1987; 36: 383-393.
- Wu Y, Liu Y. Variable selection in quantile regression. Statistica Sinica. 2009; 19: 801-817.
- Barrodale I, Roberts FDK. An improved algorithm for discrete 1 linear approximation. SIAM Journal on Numerical Analysis. 1973; 10: 839-848.
- Portnoy S, Koenker R. The gaussian hare and the laplacean tortoise: Com-putability of squared-error vs absolute error estimators, (with discussion). Statistical Science. 1997; 12: 279-300.
- Kocherginsky M, He X, Mu Y. Practical con_dence intervals for regression quantiles. Journal of Computational and Graphical Statistics. 2005; 14: 41-55.
- Gutenbrunner C, Jureckova J, Koenker R, Portnoy S. Tests of linear hypotheses based on regression rank scores. Journal of Nonparametric Statistics. 1993; 2: 307-331.
- Zhou KQ, Portnoy SL. Statistical inference on heteroscedastic models based on regression quantiles. Journal of Nonparametric Statistics. 1994; 9: 239-260.
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association. 2001; 96:1348-1360.
- Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2006; 101: 1418-1429.
- Brown R, Charters D, Gunz S, Haddow N. Colliding interests - age as an automobile insurance rating variable: Equitable rate-making or unfair discrimination? Journal of Business Ethics. 2007; 72; 103-114.
- Brockman MJ, Wright TS. Statistical motor rating: making e_ective use of your data. Journal of the Institute of Actuaries.1992; 119: 457-543.
- MLCES. (1999). Medical large claims experience study. Society of Actuaries.
- Bondell HD, Reich BJ, Wang H. Noncrossing quantile regression curve estimation. Biometrika. 2010; 97: 825-838.